Introduction
The proper design of structures and reliability of the microelectromechanical systems (MEMS) rely on the knowledge of the mechanical properties of the used materials that make up the structural components. The devices developed in this field, are necessarily very small, and so the processing techniques and the microstructures of the materials used in these devices may differ significantly from bulk structures. Hence, it is not possible to assume that the mechanical properties measured from a bulk specimen of a material will apply when the same material is used in MEMS. Actually, different techniques have been used to determine the mechanical properties of micromachined structures, especially residual stress, strength and Young's modulus [1].
The Young's modulus of materials is a key parameter for mechanical engineering design. It describes the elastic response of a material and relates stress and strain. In bulk samples the Young's modulus is often measured by loading a specimen under tension and measuring displacement as a function of stress for a given length [2]. While this is far more difficult for small structures, it can be achieved with careful experimental techniques.
For instance, a measurement that can reveal the Young's modulus of a material is the determination of the natural resonance frequency by using microcantilever which can provide information on the mechanical properties of the structural material [3]. A cantilever beam can be deflected by pushing down on the free end with a nanoindenter [4]. The nanoindenter can monitor the force applied and the defection and simple beam theory can convert the displacement into strain in order to obtain Young's modulus. Similar techniques involve pulling down a cantilever beam by means of an electrostatic or mechanical force, which can be applied using an optical interferometry [5] or contact profiler [6] respectively. In both cases, the deflection of the beam at a given electrostatic or mechanical force depends on the Young's modulus.
Stylus surface profiler has been already used to calculated silicon nitride (Si3N4) materials [6,7]. Tai et al. measured two micromechanical structures using a stylus type surface profiler in order to determine de Young's modulus of a silicon nitride and polycrystalline silicon bridges [8]. Meanwhile, Denhoff et al. performed measurements on silicon nitride bridges in order to define de residual stress on films and Young's modulus by using two different surface profilers [9]. Lately, McShane et al. performed a study to determine Young's modulus by scanning with the profiler silicon nitride microcantilever beams [10]. However, a wide range of Si3N4 Young's modulus has been reported. It can be due to the fact that the grown silicon nitride was performed in different ways or alternatively may be due to a lack of calibration of the stylus force profiler for the system used by those authors or simply a cause of the incomplete assessment of the beam bending over its entire beam's length.
In this work, we reported a stylus force calibration methodology using a silicon microcantilever standard for accurately measuring Young's modulus from Silicon Nitride (Si3N4) beams, 200 μm, 100 μm and 50μm wide, using a surface profiler. The silicon microcantilever standard has been mechanically characterized and its behaviour can be described beforehand for a given applied force, allowing precise mechanical analysis and reducing the uncertainty in measurements by profilometry presented in other works.
Experimental details
The Figure 1 shows a commercial calibrated silicon microcantilever (Si cantilever) which was used to carry out the stylus force profiler calibration. The Si cantilever nominal manufacture dimensions are 429 μm x 29 μm x 3.7 μm (LxWxt) with a manufacturer spring constant (k) of 0.65 N/m which was verified in a MultiMode Atomic Force Microscopy. This last method is based on modeling the cantilever as a simple harmonic oscillator in equilibrium with its surroundings. In order to estimate the spring constant the AFM measures the cantilever fluctuations in the time domain, after that the main square cantilever displacement is determined integrating the area under a power spectral density curve [11].

Figure 1 SEM image of Si cantilever beam, this product is used as reference cantilever for calibrating the stylus force profilometer.
The silicon nitride (Si3N4) microcantilevers fabrication was performed from a Si3N4 layer which is deposited on a silicon (Si) substrate; later a Si3N4 etch is performed in order to define the cantilever geometry. Finally, a selective etching process is used to obtain the Si3N4 microcantilever, as can be seen in the Figure 2.

Figure 2 Cross section SEM image of Si3N4 microcantilever beam which were measured by calibrated stylus force profiler.
In this work a Bruker profiler (Dektak 150) was used in order to measure Si3N4 Young's Modulus. This profiler has a diamond stylus of 5 μm radius with a 0.1 nm vertical resolution.
The calibration of the stylus profiler as well as the Si3N4 Young's Modulus measurements were carried out according to the follow procedure. The microcantilevers were basically fixed on the profiler work stage; the stylus was brought into contact with the microcantilevers base where the stylus was moved over the entire length of the cantilever resulting in a deflection thereof. The measurement was made several times for each microcantilever from different samples, verifying for any deformation caused by the applied force, which would result in an off measurement, easily identifiable as a microcantilever failure.
Results and discussion
The applied force dependence of Si cantilever deflection is shown in Figure 3. We applied a range of forces (19.61 μN to 68.63 μN) on Si cantilever in order to cover the force rate available by the Bruker stylus profiler. However, these forces were also chosen because at larger values of force the Si cantilevers were broken, thus exceeding the yield strength of material. The Si cantilever experimental deflections were plotted in open symbols as can be seen in Figure 3.
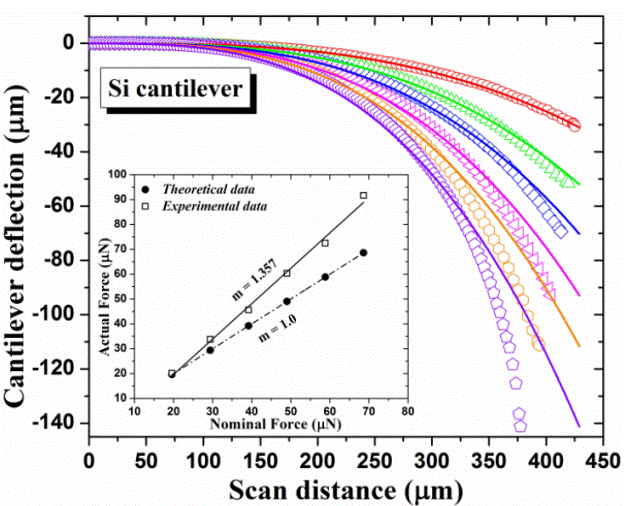
Figure 3 Si Cantilever deflection vs scan distance at different forces (open symbols). The solid lines represent the lines fitted using the Euler-Bernoulli equation. The inset depicts a comparison between theoretical (filled circles) and experimental data (open squares).
Euler-Bernoulli equation [12] describes the theoretical cantilever beam deflection (δ) which was used in order to calculate the real force.
where L, is the cantilever beam length; E, is the Young's modulus and I, is the cantilever beam second moment of inertia (bending moment). These parameters are essentially constants which are dependant of the geometry and material properties. The Silicon Young's modulus was calculated from the equation E = (k4L3)/wt3 by using spring constant value predetermined by the manufacturer as well as the Si cantilever dimensions above described. The Silicon Young's modulus result was 139 GPa which is in agreement with those previously reported for silicon material [13,14].
Finally, the force F, was the only fitting parameter in order to satisfy the Euler-Bernoulli equation. In Figure 3 can be seen the Si cantilever beam deflections described by the Equation 1 (solid lines) fitted to the experimental deflections (open symbols). The fit is completed when the end of cantilevers matched, thus, the force values (experimental data) of the stylus profiler are gotten. It can be observed a good fit for small forces, however a not good fit is presented in the case of large force.
The inset of Figure 3 depicts the nominal force vs actual force where the nominal force means the set force values on the profiler by the manufacturer (Bruker) and actual force represents the physical force.delivered by the stylus profiler. The filled circle symbols are the theoretical data (see Table 1) which represent the normal behavior of profiler, that is, the ratio between the nominal force and actual force has a linear dependence (m =1.0). However, in the case of the experimental data (open squared symbols) no linear dependence is presented (m = 1.357) because the actual force is larger than the nominal force as can be seen in the Table 1.
The differences between the experimental and theoretical data can be related to lack of the stylus calibration. In order to calibrate the stylus, other measurements on Si cantilever were performed. In this case the force values applied on Si cantilever were determined from the experimental data slope given by this expression y = 1.357 (x) - 5.294, (solid line in the inset of Figure 3). We can see these forces in the Table 1 as New Forces.
The Figure 4 shows the Si cantilever vs scan distance at different forces. We can notice a less deflection in the Si cantilever (open symbols) with respect to those shown in the Figure 3. It is also possible to observe a better fit of Si cantilever beam deflections described by the Equation 1 (solid lines).
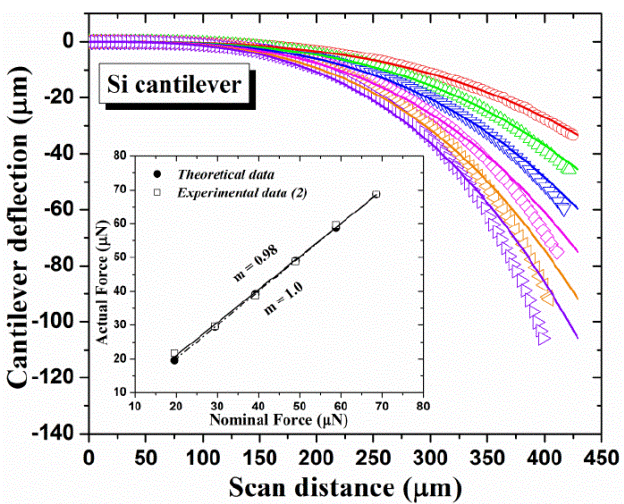
Figure 4 Si Cantilever deflection vs scan distance at different forces (open symbols). The solid lines represent the lines fitted using the Euler-Bernoulli equation. The inset depicts a comparison between theoretical (filled circles) and experimental data (open squares).
The force values (experimental data (2)) of the stylus profiler were gotten using the equation Euler-Bernoulli, as can be seen in the Table 1. It is worth noting, these values are almost the same to the theoretical data. Thus, the experimental data (2) exhibits a similar slope (m = 0.98) with respect to the theoretical data (m = 1.0) as can be seen in the inset of Figure 4. Therefore, the stylus force profiler is finally calibrated. Similar stylus force calibration methods have been reported previously [15,16], however, they did not perform the scan over entire length of the cantilever, furthermore these methods were not performed with a calibrated silicon cantilever.
Finally, with the new forces calculated (Table 1) was possible to carried out measurement on three Si3N4 microcantilevers in order to determine the Young's modulus of this material. The Si3N4 cantilevers dimensions were 50 μm 100 μm and 200 μm wide, 500 μm long and 2 μm thick for all three samples.
At first, Si3N4 cantilever 50 μm wide was scanned because it has similar dimensions with respect to the employed Si cantilever for calibration. The Figure 5(a) shows the Si3N4 cantilever (50 μm wide) deflection vs scan distance at different forces. In this case the scanning was carried out by applying the two first forces (18.35 μm and 25.57 μm) because at higher values of these forces an excessive deflection is observed which makes it difficult to fit the experimental curves. Later, a Si3N4 cantilever 100 μm wide was scanned which is shown in the Figure 5(b). In this case the first five forces (18.35 to 47.25 μm) were applied because above these values large deflections were observed. In Figure 5(c) can be seen the deflection of a Si3N4 cantilever 200 μm wide which shows the lowest deflection (high stiffness) with respect to the others cantilevers (50 μm and 100 μm wide). In this case all new forces values were applied (18.35 to 54.47 μm).
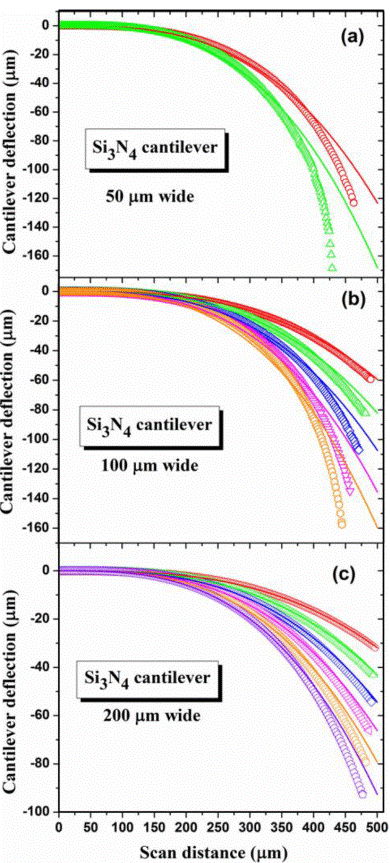
Figure 5 Silicon Nitride (Si3N4) cantilevers deflection vs scan distance at different forces for a) 50 μm, b) 100 μm and c) 200 μm wide. The solid lines represent the fit using the Equation (1).
Finally, we fitted the cantilever experimental deflections (open symbols) from Equation 1 (solid lines) in order to determine the Si3N4 Young's modulus. A Young's modulus of 219.4 ± 0.6 GPa, 230.1 ± 3.4 GPa and 222 ± 11 GPa was obtained for cantilever of 50 μm 100 μm and 200 μm wide, respectively. A_difference in standard deviations was observed which may be related to a slight twist presented in the cantilever when its width increases. The results are in good agreement with the reported data by other methods. For instance, Chuang et al.[17] obtained a Young's Modulus of 260 GPa in Silicon Nitride. Moreover, a Young's modulus of 280-290 GPa is measured for amorphous silicon nitride by scanning force microscopy [18]. The difference between Young's Modulus is related to the microcantilever thickness because in the previous works a submicrometer thickness is used; however, in this work 2 μm thick was used.
Conclusions
An alternative method to measure the elastic modulus for different materials in a rather accurate manner was presented. The ability to experimentally measure the Young's modulus of silicon nitride beams has been demonstrated. We reported Si3N4 Young's modulus around 219.4 ± 0.6 GPa, 230.1 ± 3.4 GPa and 222 ± 11 GPa for three microcantilever beams with 50 μm, 100 μm and 200 μm width, respectively. The results obtained for this approach is in good agreement with reported data by other methods. This method will be extended to measure this parameter for other materials, as well as multilayered structures of interest in MEMS. A protocol for the calibration of profilers was described. This protocol could be employed by users of these commercial instruments in order to calibrate the force exerted by the stylus, even using reference cantilever structures which could be considered to facilitate necessary calibration tasks.











 nueva página del texto (beta)
nueva página del texto (beta)


