1. Introduction
Ternary intermetallic alloys with X2YZ stoichiometric composition are known as full Heusler alloys. These materials have attracted attention due to several properties such as half-metallicity, ferromagnetism, magnetocaloric, magneto-optical, thermoelectricity, ferromagnetic shape memory effect, etc. Heusler alloys with space group
Recently, structural and magnetic properties of Co2FeSi thin films and Co2FeSi1-xBx Heusler alloys have been reported by Hazra et al. (2016) and Ramudu et al. (2015), respectively. The magnetic properties of Co2CrSi, Co2MnSi and Co2FeSi have been previously studied (Antonov et al., 2008; Kandpal et al., 2006; Kumar et al., 2009; Rai et al., 2011). However, they have not addressed the mechanical properties of these magnetic alloys which is an important factor for handling the component made of these alloys. In the present work, electronic structural, magnetic and mechanical properties of Co2MSi (M = Cr, Mn, Fe) Heusler alloys have been investigated using the density-functional theory (DFT) approach.
Recently, Mohankumar et al. (2015) reported the half-metallic property of disordered B2 structure of Co2FeSi. They have also described that the half-metallicity vanishes at the moderate percentage of B2 disorders due to the creation of new states at the Fermi level (EF) in the minority density of states (DOS) but at low and high levels of disorders, the half-metallicity has been retained. Further, Seema et al. (2015) studied the effect of disorder on the electronic, magnetic and optical properties of Co2CrZ (Z= Al, Ga, Si, Ge) Heusler alloys and Guezlane et al. and Amari et al. have studied Co2CrxFe1-xX (X = Al, Si) and Co2FeGe1-xSix (x = 0, 0.5, 1) Huesler alloys using first-principle calculations (Amari et al., 2016; Guezlane et al., 2016).
Present work is thus concerned with a comprehensive and consistent approach to explore the electronic structure, single crystal elastic and polycrystalline bulk mechanical properties of ordered Co2MSi (M = Cr, Mn, Fe) Heusler alloys in L21 structure using first-principle total energy calculations. The results obtained in the present study have been compared with experimental and theoretical values wherever available.
2. Methodology
The DFT calculations (Hohenberg & Kohn, 1964; Kohn & Sham, 1965) have been executed using Vienna ab initio simulation package (VASP) (Cms.mpi.univie.ac.at/vasp/) to study the electronic structure, magnetic and elastic properties of the Heusler alloys. The projected augmented plane wave (PAW) pseudopotential and generalized gradient approximations (GGA) have been utilized for exchange correlation energy with the Perdew-Burke-Ernzerhof (PBE) function (Perdew et al., 1996). It is well known that the local density approximations (LDA) or the generalized gradient approximations (GGA) functions underestimate the energy band gaps and can give smaller or less than fifty percentage energy band gaps. Lack of derivative discontinuity as well as an incomplete self-interaction cancellation in the GGA exchange correlation (xc) functional are the main reasons behind the reduced/ incorrect band gap estimate. Therefore, to overcome these difficulties, more appropriate green function (GW0) (Hedin, 1965), modified Becke-Jonson (mBJ) (Tran & Blaha, 2009) and Heyd-Seuseria-Ernzerhof (HSE) (Heyd et al., 2003) methods have also been performed for the electronic structure calculations.
A plane-wave cut-off energy of 268 eV has been used after checking the convergence (Fig 1(a)). For Brillouin zone (BZ) integration, a k-point mesh based on the convergence test is used (Fig 1(b)), which is corresponding to 10(10(10 Monkhorst-Pack mesh (Monkhorst & Pack, 1976). The lattice constants have been relaxed in all the three perpendicular axes to get the minimum energy of the system which is required for the structural optimization. Relaxation is terminated until the differences between energies or forces in two consecutive steps are less than 1(10-5 eV and 0.02eV/Å,respectively.
The elastic constants have been calculated using the linear-response method implemented in VASP software. In this method, the second derivative of the total energy with respect to the strain has been utilized to calculate the elastic constants.
A schematic of the crystal structure of Co2FeSi in L21 ordered structure has been shown in Fig. 2. The unit cell consists of four atoms in a face centered cubic (fcc) cell with the atomic positions of Co at (1/4, 1/4, 1/4) and (3/4, 3/4, 3/4), Fe at (1/2, 1/2, 1/2) and Si at (0, 0, 0) in Wyckoff coordinates. The corresponding space group is
In general, Slater-Pauling rule has been followed by the d-block elements and their alloys in terms of the total spin magnetic moment (mtotal) (Pauling, 1938; Slater, 1936). The net magnetic moment of a magnetic material can be defined as a difference between occupancy of valence electrons in the majority and minority spin states and is given by the relation.
where, Nv represents the total number of valence electrons and 24 represents twice the number of electrons in the minority state (Mohankumar et al., 2015). The total number of valence electrons (Nv) is (2 ( 9 + 6 + 4 = 28) 28 in Co2CrSi and hence the total magnetic moment is 4 µB (Kandpal et al., 2006). Similarly, the values of Nv for the Co2MnSi and Co2FeSi are 29 and 30, respectively. Therefore, the values mH are 5 and 6 µB for Co2MnSi and Co2FeSi, respectively. Further, a more common description for computing the spin polarization (P) is defined as (Pauling, 1938).
where
3. Results and discussion
Calculated lattice constants, site resolved magnetic moment, total magnetic moment, and spin polarization of L21 ordered Co2MSi (M = Cr, Mn and Fe) Heusler alloys are summarized in Tables 1 - 2.
Table 1 Equilibrium lattice constants (a) for Co2MSi (M= Cr, Mn, Fe). The experimental and other available theoretical values are also given for comparison (Alhaj et al., 2013; Amari et al., 2016; Antonov et al., 2008; Guezlane et al., 2016; Kandpal et al., 2006; Rai et al., 2011; Raphael et al., 2002; Seema et al., 2015; Niculescu et al., 1977; Umetsu et al., 2014; Wurmehl et al., 2005; Yin et al., 2013; Zhu et al., 2014)
| System | Lattice constant (Å) | ||
|---|---|---|---|
| Experimental | Theoretical | Present study | |
| Co2CrSi | 5.65a | 5.699b, 5.645c, 5.634d, 5.657e |
5.659 |
| Co2MnSi | 5.654f | 5.651g, 5.627d |
5.655 |
| Co2FeSi | 5.658h, 5.64i, 5.636j |
5.545k, 5.63g, 5.634c, 5.618l, 5.578m, 5.631m |
5.640 |
Ref.
b (Rai et al., 2011)
j (Yin et al., 2013)
l (Zhu et al., 2014)
Table 2 Calculated magnetic moments (using GGA, GW0, MBJ and HSE06) mCo, mM (M = Cr, Mn, Fe) and mSi is in bohr magneton (µB) as well as DOS for spin up ρ↑ (EF) and spin down ρ↓ (EF) at fermi level and spin polarization (P) for Co2MSi (M= Cr, Mn, Fe). The experimental and other available theoretical values are also given for comparison (Antonov et al., 2008; Alhaj et al., 2013; Chen et al., 2006; Guezlane et al., 2016; Kandpal et al., 2006; Kandpal et al., 2007; Niculescu et al., 1977; Rai et al., 2011; Raphael et al., 2002; Seema et al., 2015; Wurmehl et al., 2005).
| System | Magnetic moment (µB) | Spin polarisation | ||||||
|---|---|---|---|---|---|---|---|---|
| mCo | mM | mSi | mtotal | ρ↑(EF) | ρ↓(EF) | P (%) | ||
| Co2CrSi | Present study GGA GW0 mBJ HSE06 |
0.990 | 1.995 | -0.041 | 3.934 | 5.000 | 0.000 | 100 |
| 0.997 | 1.973 | -0.039 | 4.005 | 100 | ||||
| 1.000 | 1.968 | -0.034 | 4.000 | 100 | ||||
| 0.997 | 2.312 | -0.079 | 4.000 | 100 | ||||
| Others GGAb mBJb |
0.980a | 2.102a | -0.055a | 4.006a | 100a | |||
| 0.953c | 2.258c | -0.160c | 4.004c | 100c | ||||
| 1.000d | 2.030d | 4.006d | 100d | |||||
| 0.980e | 2.080e | 4.000e | 100e | |||||
| 1.02b | 1.85b | -0.03b | 4.00b | 100b | ||||
| 1.13b | 1.85b | -0.04b | 4.00b | 100b | ||||
| 1.02f | 1.90f | -0.04f | 4.00f | 100f | ||||
| Co2MnSi | Present study GGA GW0 mBJ HSE06 |
1.033 | 2.968 | -0.044 | 4.990 | 1.500 | 0.000 | 100 |
| 1.039 | 2.929 | -0.039 | 4.991 | 100 | ||||
| 1.143 | 2.967 | -0.057 | 5.000 | 100 | ||||
| 0.970 | 3.490 | -0.099 | 5.019 | 100 | ||||
| Experimental | 5.10g | |||||||
| Others | 1.029k | 3.058k | -0.055k | 5.031k | 100k | |||
| 1.07f | 2.87f | -0.04f | 5.00f | 100f | ||||
| Co2FeSi | Present study GGA GW0 mBJ HSE06 |
1.348 | 2.752 | -0.003 | 5.521 | 1.800 | 0.000 | 100 |
| 1.396 | 2.841 | -0.003 | 5.640 | 100 | ||||
| 1.531 | 2.944 | 0.011 | 5.8546 | 100 | ||||
| 1.494 | 3.232 | -0.013 | 6.000 | 100 | ||||
| Experimental | 6.00h, 5.91i | |||||||
| Others GGAb mBJb GGAk |
1.224j | 2.709j | -0.033j | 5.125j | 100j | |||
| 1.37b | 2.75b | -0.003b | 5.47b | 100b | ||||
| 1.54b | 2.96b | -0.002b | 5.84b | 100b | ||||
| 1.39k | 2.85k | 5.56k | 100k | |||||
Ref.
a (Rai et al., 2011)
ck (Kandpal et al., 2006)
Lattice parameters of all the three alloys calculated in the present study are in good agreement with previously reported experimental and theoretical values (Alhaj et al., 2013; Amari et al., 2016; Antonov et al., 2008; Guezlane et al., 2016; Kandpal et al., 2006; Niculescu et al., 1977; Rai et al., 2011; Raphael et al., 2002; Seema et al., 2015; Umetsu et al., 2014; Wurmehl et al., 2005; Yin et al., 2013; Zhu et al., 2014). It is well known that only Co and Cr/Mn/Fe atoms carry magnetic moments, while Si atom has a negative moment (Alhaj et al., 2013; Antonov et al., 2008; Chen et al., 2006; Guezlane et al., 2016; Kandpal et al., 2007; Kandpal et al., 2006; Rai et al., 2011; Raphael et al., 2002; Seema et al., 2015; Niculescu et al., 1977; Wurmehl et al., 2005). In the present study, the total magnetic moment for Co2CrSi; Co2MnSi and Co2FeSi using (GGA, GW0, mBJ and HSE06) approximations are estimated to be (3.934, 4.005, 4.000 and 4.000) µB; (4.990, 4.991, 5.000 and 5.019) µB and (5.521, 5.640, 5.8546 and 6.000) µB, respectively (Table 2). The values of total magnetic moment for these alloys are in accordance with the Slater-Paulling rule and agree with previously reported theoretical and experimental values (Antonov et al., 2008; Alhaj et al., 2013; Chen et al., 2006; Guezlane et al., 2016; Kandpal et al., 2006; Kandpal et al., 2007; Niculescu et al., 1977; Rai et al., 2011; Raphael et al., 2002; Seema et al., 2015; Wurmehl et al., 2005). It may be noted that the values calculated using HSE06 approximation are very close to the experimentally reported values (Table 2).
The band structures and density of states (DOS) for spin-up and spin-down for all the three alloys in GGA, GW0, mBJ and HSE approximations have been calculated. The band structures and DOS for all the three alloys in GGA and HSE approximations are shown in Figs. 3 - 8. It is to be noted that up and down spin states are depicted using red and blue colours in the band structures. The total DOS are shown with black colour whereas the partial DOS are represented using different colours. The atomic contributions for M (M = Cr / Mn / Fe) atoms are higher than Co atom whereas the atomic contribution of Si atom is negligible. The atomic contributions are mainly due to Co (d), M(d) and Si(p) orbitals. The bonding in all the three alloys are due to Co(d)(M(d) atomic interactions.

Figure 3 For Co2CrSi alloy under GGA (a) Band structure. Up and down spin states have been represented using red and blue colours, respectively. (b) Total DOS (black) and partial DOS of individual atoms. Scales on the top and the bottom axes are to be used to read the total and partial DOS, respectively.

Figure 4 For Co2CrSi alloy under HSE approximation (a) Band structure. Up and down spin states have been represented using red and blue colours, respectively. (b) Total DOS (black) and partial DOS of individual atoms. Scales on the top and the bottom axes are to be used to read the total and partial DOS, respectively.

Figure 5 For Co2FeSi alloy under GGA (a) Band structure. Up and down spin states have been represented using red and blue colours, respectively. (b) Total DOS (black) and partial DOS of individual atoms. Scales on the top and the bottom axes are to be used to read the total and partial DOS, respectively.
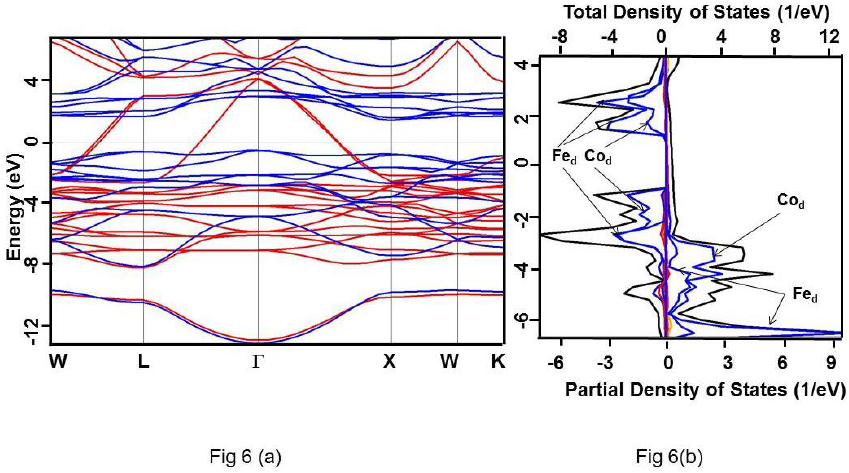
Figure 6 For Co2FeSi alloy under HSE approximation (a) Band structure. Up and down spin states have been represented using red and blue colours, respectively. (b) Total DOS (black) and partial DOS of individual atoms. Scales on the top and the bottom axes are to be used to read the total and partial DOS, respectively.

Figure 7 For Co2MnSi alloy under GGA (a) Band structure. Up and down spin states have been represented using red and blue colours, respectively. (b) Total DOS (black) and partial DOS of individual atoms. Scales on the top and the bottom axes are to be used to read the total and partial DOS, respectively.

Figure 8 For Co2MnSi alloy under HSE approximation (a) Band structure. Up and down spin states have been represented using red and blue colours, respectively. (b) Total DOS (black) and partial DOS of individual atoms. Scales on the top and the bottom axes are to be used to read the total and partial DOS, respectively.
It is clearly evident that the calculated DOS for all the three compounds show a half metallic behavior. The value of DOS at Fermi level (EF) vanishes for the down-spin whereas shows finite values for the up-spin for Co2CrSi. This reflects half-metallicity and ferromagnetism in Co2CrSi. A similar behavior can be observed for Co2MnSi and Co2FeSi alloys. The band structure and DOS depict band gap in all the three alloys.
Calculated band gap for Co2CrSi using GGA, GW0, mBJ and HSE methods are 0.780, 0.860, 1.25 and 2.93 eV, respectively (Table 3). The calculated band gap value using GGA and mBJ are close to the other reported values (Alhaj et al., 2013; Chen et al., 2006; Guezlane et al., 2016; Rai et al., 2011; Seema et al.,2015). Similarly, band gap for Co2MnSi using GGA, GW0, mBJ and HSE methods are 0.720, 0.840, 1.74 and 2.78 eV, respectively (Table 3) and are in good agreement with earlier reported values (Antonov et al., 2008; Alhaj et al., 2013).
Table 3 Calculated energy gap (Eg) (using GGA, GW0, MBJ and HSE06) in spin up and spin down polarization at fermi level (EF) for Co2MSi (M= Cr, Mn, Fe) for the ((( site symmetry. The experimental and other available theoretical values are also given for comparison (Antonov et al., 2008; Alhaj et al., 2013; Chen et al., 2006; Guezlane et al., 2016; Kandpal et al., 2006; Rai et al., 2011; Seema et al.,2015).
| System | Eg↑ (eV) | Eg↓(eV) | ||||
|---|---|---|---|---|---|---|
| GGA | GW0 | mBJ | HSE06 | |||
| Co2CrSi | Present study | 0.0 | 0.780 | 0.860 | 1.25 | 2.93 |
| Others | 0.0 | 0.910a | ||||
| 0.0 | 0.563f | |||||
| 0.0 | 0.720g | |||||
| 0.0 | 0.91b | 1.63b | ||||
| 0.0 | 0.87c | |||||
| Co2MnSi | Present study | 0.0 | 0.720 | 0.840 | 1.74 | 2.78 |
| Others | 0.0 | 0.760d | ||||
| 0.0 | 0.82c | |||||
| Co2FeSi | Present study | 0.0 | 0.680 | 0.820 | 1.95 0.86 (X(X) |
3.50 2.23 (X(X) |
| Others | 0.0 | 1.000e | ||||
| 0.0 | 0.94b | 1.77b | ||||
Ref.
a (Rai et al., 2011)
The band gap for Co2FeSi using GGA; GW0; mBJ and HSE methods are 0.680 (Γ-Γ); 0.820 (Γ-Γ); 1.95 (Γ-Γ), 0.86 (X(X); and 3.50(Γ-Γ), 2.23 eV (X(X); respectively (Table 3). The calculated band gap value using GGA and mBJ are close to the other reported values (Guezlane et al., 2016; Kandpal et al., 2006). It is to be noted that the band gaps for Co2CrSi and Co2MnSi alloys have been obtained for the (Γ-Γ) site symmetry whereas for Co2FeSi alloy, it has been obtained for the X(X site symmetry also. Therefore, band gap for Co2FeSi are given for both (Γ-Γ) and X( X site symmetries (Table 3).
Two-dimensional charge density distribution of all the three alloys in the (001) and (110) planes are shown in Figs. 9-11. All the three alloys display strong electronic interactions for Co-M and M-M type bonds whereas relatively weak interactions for the Co-Si and M-Si type bonds. The strong bonding is due to Co(d) and M(d) atomic interaction. All the Co2MSi alloys show mixed metallic and covalent bonding.
The single crystal elastic properties for cubic materials are described by three independent elastic constants namely, C11, C12 and C44 respectively and are given in Table 4. The nature of metallic bonding of cubic material can be predicted based on Cauchy pressures (Cp) (Pettifor & Aoki, 1991) which is defined as
Table 4 Calculated single crystal elastic constants (Cij) and anisotropy factor (A) for Co2MSi (M= Cr, Mn, Fe).
| System | C11 (GPa) |
C12 (GPa) |
C44 (GPa) |
A | |
|---|---|---|---|---|---|
| Co2CrSi | Present study | 303 | 197 | 159 | 3.00 |
| Co2MnSi | Present study | 222 | 170 | 124 | 4.73 |
| Co2FeSi | Present study | 248 | 183 | 113 | 3.42 |
The negative Cauchy pressure indicates more directional bonding whereas positive value means predominant metallic bonding. The calculated values of Cauchy pressures of all the alloys are positive (Table 5). Though charge density analysis indicates mixed metallic and covalent bonding, analysis based on Cauchy pressure clearly points towards the presence of predominantly metallic bonds in these alloys.
Table 5 Calculated values of Cauchy pressures (CP) and Born stability criteria (BSC) for Co2MSi (M= Cr, Mn, Fe).
| system | CP (GPa) |
(BSC)1 (GPa) |
(BSC)2 (GPa) |
(BSC)3 (GPa) |
|---|---|---|---|---|
| Co2CrSi | 38 | 159 | 106 | 696 |
| Co2MnSi | 47 | 123 | 52 | 562 |
| Co2FeSi | 69 | 113 | 66 | 612 |
The values of elastic constants can be used to provide the information about the stability of these alloys. The Born stability criterion for cubic materials is given in equation (4) (Born, 1940; Fedorov, 1968).
The calculated elastic constants have been used to assess the stability of these alloys. Since all the criteria are satisfied for all the compounds, it can be concluded that they are mechanically stable (Table 4).
Zener anisotropy factor (A) for cubic materials is defined below.
Unity value of ‘A’ suggests elastically isotropic crystal while, any deviation from unity indicates anisotropy. The values of anisotropic factor (A) obtained in present study for these alloys are away from unity indicating that the Heusler alloys studied here are elastically anisotropic (Table 4). It may be noted that the extent of anisotropy is very high for Co2MnSi followed by Co2FeSi and Co2CrSi alloys.
The effective elastic modulus of polycrystalline cubic materials can be evaluated from the elastic constants by following two approximations namely, the Voigt (1928) and Reuss (1929) that provide information about the upper and lower limits of modulus. These are defined as
where B is bulk modulus while GV and GR are shear modulus values obtained by Voigt and Reuss approximations, respectively.
The average value of these two estimates mentioned above is given by Hill (1952) approximation for cubic, hexagonal and orthorhombic materials. The Voigt-Reuss-Hill (VRH) average values are given by
where, B (=BH), G (=GH), E and ( are bulk modulus, shear modulus, Young’s modulus and Poisson’s ratio, respectively.
The calculated values of B, G and E for these alloys (Table 6) exhibit maximum value for Co2CrSi followed by Co2FeSi and Co2MnSi alloys. The calculated values for B for all the three alloys are in close agreement with the previously theoretically reported values (Alhaj et al., 2013; Amari et al., 2016). It is to be noted that the B value for Co2FeSi is also in good agreement with the experimentally obtained value (Garg & Vijayakumar, 2011). The calculated values of Poisson’s ratio (v) shows maximum value for Co2CrSi followed by Co2MnSi and Co2FeSi alloys.
Table 6 Polycrystalline mechanical properties such as Bulk modulus (B), Shear Modulus (G), Young’s modulus (E), G/B ratio and Poisson’s ratio (() for Co2MSi (M= Cr, Mn, Fe). The other available experimental and theoretical values are also given for comparison (Alhaj et al., 2013; Amari et al., 2016; Garg & Vijayakumar, 2011).
| system | B (GPa) |
GV (GPa) |
GR (GPa) |
G (GPa) |
E (GPa) |
ʋ | G/B | |
|---|---|---|---|---|---|---|---|---|
| Co2CrSi | Present study | 223 | 117 | 88 | 103 | 267 | 0.300 | 0.442 |
| Others | 239a | |||||||
| Co2MnSi | Present study | 187 | 85 | 49 | 67 | 178 | 0.340 | 0.358 |
| Others | 227a | |||||||
| Co2FeSi | Present study | 205 | 81 | 57 | 69 | 186 | 0.349 | 0.338 |
| Others | 204b, 210b | |||||||
| Expt. | 240c |
The values of B and G can also be utilized for the brittle and ductile behavior of materials (Pugh, 1954). This can be predicted by taking the ratio G/B. The ratio (G/B) > 0.57 is associated with brittleness. Present calculation clearly indicates that all the three alloys in present study are ductile.
4. Conclusions
Structural stability and mechanical properties of Co2MSi (M= Cr, Mn, Fe) Heusler alloys in L21 structure have been investigated using DFT within GGA.
The lattice constant of these alloys show close values with the previously reported experimental and theoretical data, respectively.
The magnetic moment (m) values obtained in present study (using GGA, GW0, mBJ and HSE methods) for all alloys are in accordance with Slater-Pauling rule.
All the alloys have predominantly metallic bonding.
These alloys are half-metallic as well as ferromagnetic as inferred from their band structure and density of states (DOS).
All the three alloys are anisotropic. The extent of anisotropy is highest for Co2MnSi followed by Co2FeSi and Co2CrSi alloys.
All the three alloys obey the Born stability criteria and are associated with a ductile behavior based on G/B ratios.
Conflict of interest
The authors have no conflict of interest to declare.
Financing
The authors received no specific funding for this work.











 nueva página del texto (beta)
nueva página del texto (beta)







