Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Problemas del desarrollo
versión impresa ISSN 0301-7036
Prob. Des vol.53 no.208 Ciudad de México ene./mar. 2022 Epub 06-Jun-2022
https://doi.org/10.22201/iiec.20078951e.2022.208.69761
Articles
Wage share and structural heterogeneity in Peru: diagnosis and simulations
aPostgraduate School of the Universidad del Pacífico, Peru. Email address: g.alarcotosoni@up.edu.pe .
This article examines the effect of structural heterogeneity on income distribution and presents the evolution of the wage share in Gross Domestic Product (GDP) and Gross Value of Production (GVP) for the period 1950-2017. The article calculates and analyzes intersectoral differences in labor productivity and wages in various sectors of the Peruvian economy. Based on an input-output (IO) model for 14 economic activities, projections of final demand for 2018-2030, and trends in the production structure and primary input matrix, this article concludes that, in various scenarios, the wage share in the GVP will present a downward trend between 2018 and 2030. Both the analysis of structural heterogeneity and the results of the simulations demonstrate the importance of productive structure when seeking to understand severe inequality.
Key Words: wage share; structural heterogeneity; input-output table; factor income distribution
En el presente texto se discute cómo la heterogeneidad estructural afecta la distribución del ingreso y se presenta la evolución de la participación salarial en el Producto Interno Bruto (PIB) y el Valor Bruto de la Producción (VBP) entre 1950-2017. Se determinan y analizan las diferencias intersectoriales de la productividad del trabajo y las remuneraciones de los diferentes sectores de la economía peruana. Mediante un modelo insumo-producto (IP) con 14 actividades, proyecciones de la demanda final 2018-2030, tendencias de la estructura productiva y en la matriz de insumos primarios se determinan en diversos escenarios, que la cuota salarial en el VBP tenderá a reducirse entre 2018 y 2030. Tanto el análisis de la heterogeneidad estructural como los resultados de las simulaciones reflejan la importancia de la estructura productiva para entender la elevada desigualdad.
Palabras clave: participación (cuota) salarial; heterogeneidad estructural; tabla insumo-producto; distribución factorial del ingreso
Clasificación JEL: C67; D31; E25; J31
1. INTRODUCTION
Many factors must be taken into consideration when seeking to understand income distribution. Income distribution is a multidimensional and multifactorial phenomenon based on the structure of wealth distribution. Income distribution is not only shaped by economic factors, but also history, institutions, the role of the state, power structures, and socio-political dynamics. At a more instrumental level, international economic variables, changes in the productive structure, fiscal and tax policy, and numerous macroeconomic variables also play their part. Financial and labor market variables also have a role (Alarco et al., 2019).
Traditionally, most studies focus on the impacts of macroeconomic, financial, tax, and fiscal policy variables on income distribution. However, there is only limited literature on the impacts of the productive structure and productivity on inequality. One relevant study on the subject was developed by Quaresma de Araujo (2013) for Brazil, in which he takes up the position traditionally held by the Economic Commission for Latin America and the Caribbean (ECLAC) that structural heterogeneity is one of the main causes of inequality. From this perspective, industrial policies should be oriented towards modifying the productive structure, incorporating technical progress, and raising productivity levels. This research postulates that high rates of economic growth and industrial policies that promote greater participation among engineering-intensive sectors can contribute to better distributive outcomes, a higher wage share of output, and greater employment.
This article intends, first of all, to explain the wage share of output in the Peruvian economy based on the evolution of its production structure, productivity, and wages. This is based on the understanding that the latter is heterogeneous and that it fluctuates in response to a particular internal dynamic, the final demand, and technological changes taking place within the various productive sectors. Second, this article projects wage shares up to 2030, factoring in various passive scenarios of final demand, input-output (IO) relations, and changes in the various components of added value.
The impacts that other macroeconomic variables from the international economy may have on the factorial distribution of income are not taken into consideration, and neither are financial and labor market variables or the degree of concentration in the economy. This article works from the hypothesis that these structural changes and trends alone would lead to a reduction in the wage component of output, without considering the impacts of reduced labor content per unit of output as a result of the COVID-19 pandemic. The articles’s third objective is to expound a methodology that could be used for diagnosing and calculating forward projections for other economies in the region.
This article is divided into four sections, plus the introduction, conclusions, and Annex. The first section offers a brief discussion on structural heterogeneity and inequality. The second section presents and analyses data on the wage share of Gross Domestic Product (GDP) and Gross Value of Production (GVP), the evolution of the average output per worker by productive sectors, and its inverse, the labor content per unit of output, i.e. the rate of salaried workers (share of dependent workers in the total employed). The third section explains the changes in the wage share of the whole economy with reference to changes in the production structure. The final section includes both the IO methodology for assessing different wage share scenarios with trends in the production structure to 2030, as well as the different assumptions and findings of these exercises. The IO table for 2017 is included in the Annex.
Several limitations of the article, requiring further development, are that it does not address the issue of wealth distribution or personal income distribution. The IO tables prior to 1969 have very different methodologies and sectoral classifications than those developed later. Similarly, there is no detailed information available for the IO models between 1994 and 2007. Productivity and technological changes are calculated using historical sectoral statistical information, without any detailed analysis or active future projections. For the sake of simplicity, this article employs a table with just 14 productive sectors, disregarding intra-sectoral differences. Furthermore, analysis does not factor in the problems of the self-employed or the self-employed. The article does not attempt to explain political dynamics. The simulation exercises are simple, as they do not assess the impacts of factors such as different projected wage shares to 2030 on private consumption, demand, production, trade, and balance of payments, inflation, savings, to name a few, which should be addressed by another type of model. Nor does the article propose an industrial policy that maximizes employment or added value, as in Brazil.
2. STRUCTURAL HETEROGENEITY AND INEQUALITY
Structural heterogeneity establishes diverse productive structures within any given economy. The concept was developed by Pinto (1970), who pointed out that a dualistic structure would predominate in the region due to the contrast between high-productivity export enclaves and the rest of the economy characterized by low levels of productivity. Likewise, the industrialization and growth process of the mid-20th century tended to reproduce the previous heterogeneity and to make the inter-sectoral differentials of the economies greater than those observed in developed economies, fueling greater inequality and income reconcentration. Subsequently, as a result of industrial policies, the endogenization of technical progress, and international trends, the list of modern sectors expanded to include telecommunications, financial and insurance, automotive, chemical, and other non-traditional export activities., depending on each economy’s respective characteristics and mode of insertion into the international economy.
Torres (2019) notes that although the notion of structural heterogeneity is credited to Aníbal Pinto, significant contributions were also made by scholars such as Prebisch, Furtado, Rodríguez, and Sunkel, to name a few, who prefigured a structuralist theory of Latin American underdevelopment; that is, of the region's peripheral condition. The growth generated by import-substitution industrialization would reproduce the productivity differentials by class and social strata, as in the primary export model, and these asymmetries were also reflected in wage differentials between these groups.
Infante and Sunkel (2009) argue that the characteristics of an economy’s productive structure are a determinant of inequality. The authors analyze this problem for the case of Latin America, in particular Chile, describing a traditional productive stratum whose productivity and income levels were low; a modern stratum made up of export activities and large industrial and service companies on a large operational scale, which captured a decisive fraction of the local market and whose productivity per employed worker was at a level similar to the average in developed economies; and finally, an intermediate stratum. The heterogeneity of the productive apparatus is evidenced by the fact that the output per worker of the modern stratum was four times the average, 29 times that of the traditional stratum, and nearly five times that of the intermediate stratum. The authors argue that these differences in productivity were reproduced in workers’ salaries and thus constituted a determining factor in Latin America’s poor income distribution.
In the specific case of Chile, the authors used data from the 1O matrix and employment by productive sectors to identify three markedly different levels of productivity. By doing so, they found that the average productivity of mining was 15 times higher than that of agriculture, with that of construction and industry being twice and four times higher, respectively, than that of agriculture. Regarding intra-sectoral differences, for example, in agriculture, large enterprises have productivity levels seven times higher than that of small enterprises, a ratio that increases to 12 times in the case of construction and 40 times in the case of mining. Ultimately, the data show that intra-industry differences in productivity are significantly higher than inter-industry differences. On the other hand, the employment figures show that the branches of economic activity in which small enterprises have the highest labor retention capacity (including informal activities and micro-enterprises) are those with the lowest level of productivity compared to the other sectors, which correspond to the agriculture, community services, and commerce sectors. In contrast, sectors’ productivity levels increase as their capacity to absorb formal employment in medium and large enterprises improves.
Recently, Ffrench-Davis (2019) has pointed out that structural heterogeneity manifests itself in the following aspects: (i) diverse productivities among firms of different sizes and workers with very heterogeneous qualifications; (ii) diverse capacities for action and reaction, or asymmetry of response of typical agents in different markets, whether large or small entrepreneurs, high and low-skilled workers, productive investors generating GDP, or financial investors seeking economic rents; and (iii) asymmetries in the response capacities of different agents to the instability of economic activity and macro-prices. According to the author, all of these are intensified to the extent that results in a more unstable macroeconomic environment.
Távara et al. (2014) point out that Peru's aggregate productivity for the period 1960-2011 has three distinct stages or phases: growth between 1960-1975; stagnation and crisis from the mid-1960s to 1992; and growth thereafter, except for short periods of recession in the late 1990s and 2008 caused by the Asian crisis and the financial crisis in the US and European economies, respectively. Like the previous authors, they also identify high, medium, and low productivity sectors.
In this respect, productivity gaps widened during the expansion phase and even up to 1980. During the period of stagnation and crisis, the gaps narrowed because the group of sectors with the highest productivity registered a greater decline, followed by the medium productivity group. Subsequently, at the beginning of the expansion phase in 1992, the gaps widened again.
Structural heterogeneity is closely linked to inequality. A pattern of economic growth that emphasizes capital-intensive sectors over labor-intensive ones tends to reduce the overall share of wages and salaries in output, unless wages and salaries grow rapidly. On the other hand, a distributive policy aimed at reducing inequality both in income and in access to opportunities among the various groups that make up the social structure necessarily implies reducing the productive heterogeneity that characterizes the country's economic system (Infante, 2007). This applies both to profit generation in the various productive sectors and to the wage differentials between these sectors. Seen in this light, policies should be implemented to reduce the differentials produced by the asymmetry in productivity between leading-edge activities, which are competitive even at the global level, and others with low productivity levels, such as micro and small, informal enterprises. This implies that reducing inequality requires narrowing gaps in productivity, and therefore the primary (autonomous) income of the least favored sectors must be improved, starting with the modern export sectors with lower productivity (Infante and Sunkel, 2009).1
Similarly, Távara et al. (2014) argue that narrowing these gaps is crucial for building a more democratic and inclusive society in which people's well-being does not depend exclusively or mainly on social policies, whose continuity may be compromised by the availability of fiscal resources, or on political decisions. A strategy aimed at achieving productive articulation and convergence between strata and sectors will allow the Peruvian economic system to generate more equitable income and wealth distribution, a central dimension of inclusive development. To be effective, this strategy must act on exchange rate policy, competition policy, labor policy, state modernization and decentralization, and industrial policies with an emphasis on technological change and micro and small enterprises, among others. The details of any concrete proposals are beyond the scope of this paper.
3. WAGE SHARE AND PRODUCTIVITY: LONG, MEDIUM, AND SHORT TERM
Figure 1 shows the wage share relative to GDP and GVP, using annual data from the period 1950-2017. Wage share relative to GDP is presented complete with statistical information from the National Institute of Statistics and Informatics (INEI); the solid line is the observed data, while the dashed line is the non-linear Hodrick-Prescott trend. The lower dotted line, meanwhile, shows wage share relative to GVP. This line is discontinuous, given that there was a lack of complete data for every year, and has been calculated using the IO table for specific years and periods. The data for 1950, 1955, 1956, and 1961 correspond to the IO matrices prepared by the Central Reserve Bank of Peru (BCRP), presented in Gonzáles de Olarte (2015).2 The years 1969 and 1990 correspond to INEI (1990 and 1991), 1994 (INEI, 2000), and 2007-2017 (INEI, 2019).
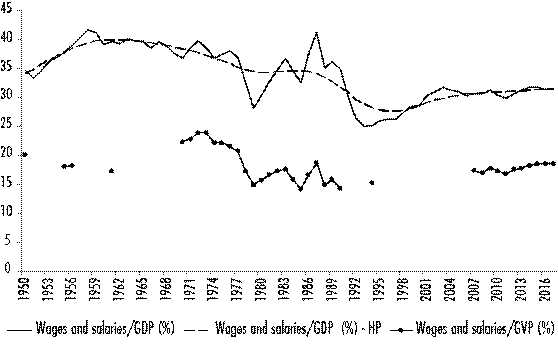
Source: compiled by the author using data from BCRP (1970) and INEI (1990, 1991, 1992, 2000, and 2019).
Figure 1 Wage share of GDP and GVP 1950-2017 (%)
The non-linear trend of the wage share relative to GDP is sinusoidal, reaching its highest value in the 1960s and its lowest value in the first five years of the 1990s. The wage share begins to decrease during the second half of the 1970s, due to the adjustment policy implemented between 1975 and 1978, after the first stage of the military government of General Velasco. The wage share also decreased significantly during the late 1980s, due to the effects of high inflation, and another drastic decrease began in the early 1990s, due to the adjustment and stabilization program implemented during the government of Alberto Fujimori. A slight upward trend began in the second half of the 1990s, which continues to the present day.3
The wage share of GVP series is understandably lower than that of GDP. The lowest values occurred in 1985 and 1990, followed by 1979. The highest values were observed in 1972 and 1973. Unfortunately, there are no reliable data prior to 1969.
Figure 2 shows the structural heterogeneity characteristic of Latin American economies. Here, the average real output per worker and real wages per worker are shown for the 14 productive sectors of the Peruvian economy into which the IO matrices have been grouped between 2007 and 2017.4 On the other hand, it should be noted that the matrix corresponding to 2007 includes 54 economic activities. Data is presented for both variables for the years 2007 (dashed line) and 2017 (solid line). The data in current soles were converted to constant soles using the deflator of each economic activity. Likewise, the data was ordered from highest to lowest value.

Source: compiled by the author using data from INEI (2019)
Figure 2 Productivity and real salaries per worker 2007 and 2017 (constant Soles 2007)
In 2007, the difference between the average real product of mining and hydrocarbons, relative to the agriculture, hunting, and forestry sector was 55 times, while in 2017 it was 50 times. In 2007, on the other hand, real remunerations had a difference of 55 times compared to 60 times in the case of 2017. The distance between real average output and real remunerations differs according to economic activity. In the case of mining and hydrocarbons, this decreased slightly from 7.6 to 7.3 times between 2007 and 2017. In the agriculture, forestry and hunting sector, meanwhile, it rose from 7.6 to 8.8 times in the same period. Regarding variations in productivity, all sectors showed increases between 2007 and 2017, with the exception of fishing and aquaculture. Regarding real average remunerations, positive variations were also recorded, with the exception of financial services, insurance and pensions; and fishing and aquaculture.
The wage share relative to GVP by economic sectors is shown in Figure 3 for the years 2007 and 2017. There are significant differences between economic activities. In 2007, differences fluctuated between 9% and 45%, while in 2017 the distance widened between 9% and 50%, reflecting greater structural heterogeneity. The data are presented from the highest to the lowest value. This figure demonstrates the importance of analyzing how changes in the productive structure impact the wage share of the economy. The sectors with the highest wage share are public administration and defense; other services; financial services, insurance, and pensions; and business services and construction. At the other extreme are the activities with the lowest wage share, such as manufacturing; transportation, storage, and mail; and electricity, gas, and water. At an intermediate level are trade; fishing and aquaculture; telecommunications; accommodation and restaurants; mining and hydrocarbons; and agriculture, hunting, and forestry. Overall, between 2007 and 2017, the wage share of the economy and that of many economic sectors rose, with the exception of financial services, insurance, and pensions; fishing and aquaculture; telecoms; accommodation and restaurants; agriculture, hunting, and forestry; electricity, gas, and water; and transportation and storage.

Source: Compiled by the authors using data from INEI (2019)
Figure 3 Wage share by economic sector 2007 and 2017 (% of GVP)
The recent improvement in the purchasing power of wages and salaries and the wage share can be seen in Figure 4; however, it is important to clarify that this only began during the second half of the 1990s. Modifying the base year and taking the 1960s or 1970s as a reference alters the picture drastically, evidencing a generalized loss of the wage share in output and purchasing power, compared to the improvement observed in recent years. Furthermore, the labor content per unit of output (inverse of the real average output per worker) fell from 27 to just over 19 workers per million soles of output between 2007 and 2017. The technological change observed for the entire economy on average substitutes workers for capital and intermediate inputs (domestic and imported).5
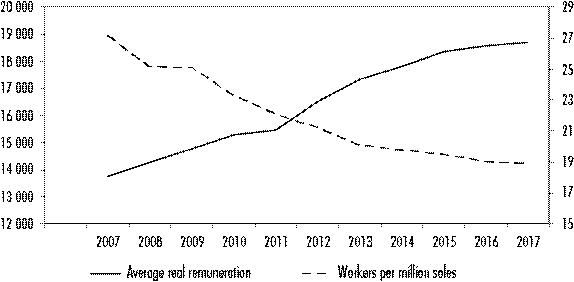
Source: Compiled by the authors using data from INEI (2019)
Figure 4 Average real remunerations and labor content per unit of output 2007-2017 (constant Soles 2007 and workers)
4. DECOMPOSITION BY EXPLANATORY FACTORS
The primary objective here is to explain the wage share of remunerations in the GVP of the economy as a whole, in relation to changes in the production structure and the wage share in the GVP by economic activity. If an economy’s pattern of economic growth is biased in favor of capital-intensive sectors where the wage share is low, the average share of the economy will tend to fall. On the other hand, where there is significant sectoral participation and economic growth is predominantly driven by these more labor-intensive sectors, the wage share of the whole economy increases. This proposal is based on the explanatory factors of the wage and salary share in an economy with various productive sectors, as proposed in Kalecki’s (1956) study of national income distribution.
This article operationalizes decomposition by applying the concept of total derivates, in an expression that depends on two multiplicative components.6 Equation (1) shows that the wage share of GVP depends on the wage share in the GVP of each of the productive sectors
Table 1 shows that changes in the production structure play a significant role in determining the wage share in the economy's GVP, both annually and throughout the period 2007-2017. Structural heterogeneity played a crucial role in determining the overall share of wages and salaries in the value of production, with the exception of the years 2008, 2010, and 2012, during which the other effect of wage share variations dominates. Structural heterogeneity had a direct impact both in periods when it decreases (especially between 2007-2008 and 2010-2011), as well as during periods in which the wage share in GVP increases, i.e. for the remaining years with the exception of 2012. More specifically, between 2010 and 2011, the sectoral structure drove a reduction in the economy's wage share due to the higher growth in the mining and hydrocarbons, transportation and communications, and construction sectors, which have wage shares below the national average and are less labor intensive.
Table 1 Contribution of the production structure and sectorial wage share of remuneration in CVP 2007-2017
| Year | Participation wage share / GVP | Annual variation | Explanatory components (%) | |||
| Change in Production structure | Change in wabe share | Combined variation | Total variation | |||
| 2007 | 17.39 | - | - | - | - | - |
| 2008 | 16.93 | -0.46 | 4.01 | 90.33 | 5.66 | 100.00 |
| 2009 | 17.81 | 0.88 | 76.80 | 22.15 | 1.05 | 100.00 |
| 2010 | 17.29 | -0.52 | 45.29 | 50.25 | 4.46 | 100.00 |
| 2011 | 16.74 | -0.55 | 55.21 | 43.17 | 1.62 | 100.00 |
| 2012 | 17.53 | 0.79 | 42.41 | 61.40 | -3.81 | 100.00 |
| 2013 | 17.83 | 0.30 | 62.35 | 37.15 | 0.50 | 100.00 |
| 2014 | 18.24 | 0.41 | 79.50 | 22.97 | -2.47 | 100.00 |
| 2015 | 18.54 | 0.30 | 55.80 | 51.66 | -7.46 | 100.00 |
| 2016 | 18.58 | 0.03 | 303.47 | -176.88 | -26.59 | 100.00 |
| 2017 | 18.61 | 0.03 | 106.11 | -0.82 | -5.29 | 100.00 |
| 2017-2007 | 1.21 | 109.23 | 0.57 | -9.80 | 100.00 | |
Source: Compiled by the authors using data from INEI (2019).
When the economy's wage share increases, the growth in the share of the output of other services; services rendered to companies; trade; and accommodation and restaurants, which are more labor intensive, also contribute to the lower share of the hydrocarbons and mining sector output. This occurs despite the fact that the financial services, insurance, and pensions sector increased its share of GVP while its wage share decreases over time.
Lindenboim et al. (2011) offer an interesting decomposition to explain the evolution of the wage share in Argentina's GVP, which will be briefly summarized here. Analysis starts from the definition of the wage share in GVP, which would be equivalent to the real pro-average remuneration per worker (w) times wage employment (EA) divided by the price index of GVP (p) times the real GVP (realGVP) of equation (3). Then, both the numerator and the denominator are multiplied by the employed population (EO) to then regroup the fractions where the wage share in the GVP would be equal to the product of the real average remuneration or unit wage cost (realREM), the inverse of the average product of labor or the labor content per unit of product (CON) and the number of salaried workers that measures the ratio between the salaried workers and workers in employment (ASAL) of equation (9).
In equation (9) the total derivative is applied to the wage share in GVP, determining seven components. The first component is the growth of real average remuneration per worker, keeping the other two variables constant; the second is the change in labor content per unit of output; and the third is the change in the wage rate, with other variables kept constant. The four final expressions are integrated into a single one as the mixed effects that include the variation of the three main explanatory components. The results of the four components are divided by the change in the wage share relative to GVP to add up to 100%.
Table 2 shows the four components that explain the variation of the wage share in GVP.7 Of the four components, the only one that maintained a negative contribution over the entire study period is the labor content per unit of output. This component also most significantly contributes to explaining the wage share at the national level, excluding events between 2008 and 2009. The general trend in the 2007-2017 period is a reduction in labor content per unit of output. Real average remuneration, meanwhile, maintained a positive contribution for the entire study period. Between 2014 and 2015 it should be noted that its explanatory contribution was higher than that of labor content per unit of output. Finally, it should be noted that, with the exception of 2015, the wage rate contributed positively to explain the increasing trend of the wage share at the national level. Mixed effects have a marginal contribution to the explanation.
Table 2 Contribution of change in average real remuneration, labor content per unit of output, and salaried workers on the share of remunerations in GVP 2007-2017
| Year | Wage share / GVP | Annual variation | Explanatory components (%) | ||||
| Change in remunerations actual perworker | Change in labor content per unit of product | Change in salaried workers | Mixed effect | Total variation | |||
| 2007 | 0.1739 | - | - | - | - | - | |
| 2008 | 0.1693 | -0.0046 | -137.27 | 283.46 | -58.93 | 12.73 | 100.00 |
| 2009 | 0.1781 | 0.0088 | 67.65 | -5.78 | 37.14 | 0.99 | 100.00 |
| 2010 | 0.1729 | -0.0052 | -118.75 | 242.91 | -33.86 | 9.70 | 100.00 |
| 2011 | 0.1674 | -0.0055 | -38.81 | 164.20 | -28.58 | 3.19 | 100.00 |
| 2012 | 0.1753 | 0.0079 | 145.43 | -86.33 | 45.66 | -4.76 | 100.00 |
| 2013 | 0.1783 | 0.0030 | 298.43 | -303.47 | 120.84 | -15.81 | 100.00 |
| 2014 | 0.1824 | 0.0041 | 115.45 | -69.62 | 55.47 | -1.30 | 100.00 |
| 2015 | 0.1854 | 0.0030 | 185.12 | -77.58 | -5.08 | -2.46 | 100.00 |
| 2016 | 0.1858 | 0.0003 | 695.47 | -1350.38 | 781.49 | -26.58 | 100.00 |
| 2017 | 0.1861 | 0.0003 | 365.71 | -456.37 | 193.43 | -2.77 | 100.00 |
| 2017-2007 | 0.0121 | 515.45 | -437.56 | 189.52 | -167.41 | 100.00 | |
Source: Compiled by the authors using data from INEI (2019).
5. SIMULATIONS OF THE WAGE SHARE WITH STRUCTURAL TRENDS TO 2030
Four scenarios are presented for projecting the wage share in the GVP to 2030, based on trends in the production structure. These simulation exercises were carried out based on the IO table methodology (Kozikowski, 1988), assuming passive projections for the different components of final demand and the different sectoral wage shares.8 The various components of final demand maintain the long-term trend between 1950-2017 and the medium-term trend between 1990-2017, capturing the changes in the reorientation of the economic model in accordance with the structural reforms established during the 1980s and 1990s. On the other hand, the trends in sectoral wage shares reflect both technological changes and the evolution of real wages during the period 2007-2017. It should be emphasized that by using the IO model with the base year 2017, all technical coefficients reflecting intersectoral relationships are kept constant from 2018 to 2030.
The projections are carried out in two stages. First, two sets of vectors are projected for final demand in the scenario for the period 2018-2030. The real components considered are final household consumption, gross capital formation, exports, and final government consumption. The change in inventories is always assumed as an average of the years 2016 and 2017. For each of the projections, a simple method was applied based on estimating the regression with respect to time with the best fit and quality of the parameters in linear, quadratic, and polynomial modes of two and three degrees.9 On the other hand, in the case of sectoral wage shares, only the average annual growth rate was determined through a semi-logarithmic regression.10 This is because these series are short, comprising the years 2007-2017. The second part consisted of projecting the wage shares relative to GVP using vectors and matrices following the formulas detailed below.
The vector of sectoral GVP (X 14*1) is obtained by pre-multiplying the matrix of domestic and imported technical coefficients (A 14*14) by the vector of production, and to which is added the vector of final demand (F 14*1) of equation (11). Next, the final demand vector can be decomposed into a matrix of final demand coefficients (D14*5) and the vector of each of the five final demand components (Z 5*1) of equation (12). The vector of primary inputs vectors or PIV: worker wages, gross operating surplus, mixed income, and other taxes (Y 4*1) is obtained by multiplying the primary input matrix (B 4*14) by the vector of GVP (X 14*1) from equation (15). Expression (16) shows the equation that would be used in the estimation when considering changes in final demand (Z 5*1) and the primary input matrix (B 4*14). The 2017 input-output matrix of the Peruvian economy is presented in the annex. All projections are made in constant 2007 soles.
The main difference between the projections of the four components of real final demand derived from the period 1950-2017 and 1990-2017 lies in the fact that the latter show higher rates than the former, except for the decreasing rates for exports and investment. In particular, considering the period 1950-2017, the annual growth rates of final household consumption would fluctuate between 4.9% and 4.6% annually, general government consumption between 5.6% and 5.1% annually, exports between 5.1% and 4.5% annually, and gross capital formation between 6.1% and 5.2% annually. In the case of the projections, considering only the data for 1990-2017, the general household consumption would grow between 6.1% and 5.8%, general government consumption between 8% and 7.3%, exports between 2.9% and 1.7%, and gross capital formation between 4.8% and 1.7% annually.
Changes in the primary input matrix or Gross Value Added (GVA) from 2018 to 2030 would be more significant. The agricultural, hunting and forestry; fishing and aquaculture; electricity, gas and water; transportation, storage; telecommunications; financial services, insurance, and pensions; and business services sectors would be the ones with a continuous reduction in the share of wages and salaries in GVP, mainly due to the reduction in labor content per unit of output discussed in the fourth section of this document. Among these, the largest reductions were in the financial sector, telecommunications, fishing and aquaculture, telecommunications, and transportation. On the other hand, according to the trends observed in the 2007-2017 period, there would be slight increases in the shares of wages and salaries in GVP in the cases of mining and hydrocarbons; manufacturing; construction; trade; accommodation and restaurants; public administration and defense; and other services. It should be noted that the projections work from the assumption that a reduction in the wage share in a productive sector has a corresponding increase in the gross operating surplus, keeping constant the sum of the national and imported technical coefficients and the sum of primary inputs. Conversely, if the wage share in GVP increases, the gross operating surplus share must be adjusted by the same magnitude.
Table 3 presents the results of the four passive simulations of the wage share in the Peruvian economy 2018-2030 based on the IO 2017 production structure trends. The first two scenarios comprise only the results of growing final demand with data from 1950 to 2017 and from 1990 to 2017. The third and fourth simulations comprise the two previous scenarios, adding in both cases the aforementioned modification in the primary input matrix, which would reflect the changes in wages and technological changes during the period 2007-2017. Here, all passive simulations show a decreasing trend relative to the base year, the most pronounced being the one resulting from the simple projection of final demand in the period 1950-2017. In second place is the projection of long-term final demand and the change in sectoral wage shares. It is noteworthy that the least negative simulations correspond to the passive projections of final demand considering only the period 1990-2017 and to the medium-term projection with the changes in sectoral wage shares.
Table 3 Passive simulations of the wage share in the Peruvian economy 2018-2030 (% of GVP)
| Years | Passive scenarios 2018-2030 | |||
| Final demand components Long term | Find demand components Medium term | Long-term final demand and changes in sectorial wage shares salariales sectoriales | Medium-term final demand and changes in sectorial wage shares salariales sectoriales | |
| 2017* | 18.61 | 18.61 | 18.61 | 18.61 |
| 2018 | 18.45 | 18.51 | 18.47 | 18.53 |
| 2019 | 18.29 | 18.41 | 18.32 | 18.44 |
| 2020 | 18.14 | 18.32 | 18.19 | 18.38 |
| 2021 | 18.01 | 18.25 | 18.08 | 18.32 |
| 2022 | 17.89 | 18.20 | 17.97 | 18.28 |
| 2023 | 17.78 | 18.15 | 17.88 | 18.25 |
| 2024 | 17.68 | 18.12 | 17.79 | 18.23 |
| 2025 | 17.59 | 18.09 | 17.71 | 18.22 |
| 2026 | 17.50 | 18.07 | 17.65 | 18.22 |
| 2027 | 17.43 | 18.06 | 17.58 | 18.22 |
| 2028 | 17.36 | 18.05 | 17.53 | 18.23 |
| 2029 | 17.29 | 18.05 | 17.48 | 18.24 |
| 2030 | 17.23 | 18.05 | 17.44 | 18.26 |
Note: *Observed values.
Source: Compiled by the authors using data from INEI (2019)
Figure 5 shows the historical information of the wage share relative to GVP over the period 1970-2017 and the four passive simulations of final demand and change in sectoral wage shares 2018-2030. As previously explained, the trends of the projections are negative in all cases. The wage share of the economy tends to decrease, however not drastically. In the long-term, the highest levels of the wage share to GVP occurred in the 1970s, while its lowest share was recorded in 1985 and 1990. From then on, the trend is slightly increasing and achieves its highest wage share in GVP in 2017. Subsequently, there would be the negative passive trend noted above. Unfortunately, it is not possible to compile a complete data series since 1970 due to the lack of official statistics of the input-output table.
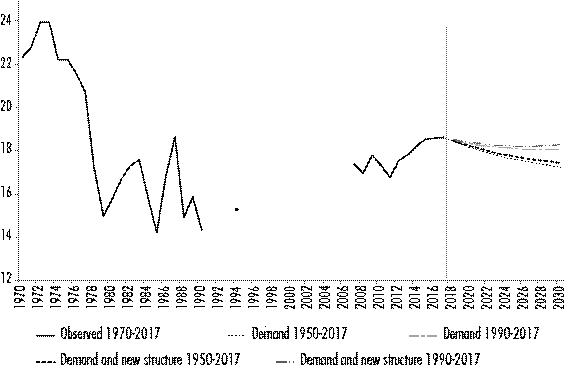
Source: Compiled by the authors using data from BCRP (1970) and INEI (1990, 1991, 1992, 2000, and 2019)
Figure 5 Trends and passive projections of the wage share 1970-2030 (% of GVP)
6. CONCLUSIONS
Structural heterogeneity exerts a significant influence on income distribution in Latin America. The initial proposal of dividing the productive structure into two sectors (traditional and modern) has evolved over time. Currently, these categories are based on three major levels of productivity, which can be opened up further when a typology is established based on the size of productive units within particular sectors. The varying patterns of production and growth associated with the evolution of internal and external demand tend to find widening differences between productivities, remunerations, and income, thereby impacting both the factorial and personal distribution of income.
The wage share in Peruvian GDP during the period 1950-2017 shows a non-linear sinusoidal trend, peaking in the 1960s with lower values in the first half of the 1990s as a result of the adjustment, stabilization, and structural adjustment programs implemented in recent decades. A slight recovery began in the second half of the 1990s, yet without reaching the previous levels observed in the 1960s and 1970s. This same dynamic can also be observed for the wage share of GVP from the 1970s onwards, although at a lower level. The lack of sufficient and consistent statistical data makes it impossible to obtain a long series for the entire study period.
Intersectoral differences in productivity per worker seem to be higher than the regional averages. The differences between the most modern and the most traditional sectors slightly reduced from 55 times to 50 times during 2007-2017. However, the differences between the highest and lowest real remunerations rose from 50 to 55 times during the same period. On the other hand, sectoral wage shares of their respective GVPs widened from a range of 9% and 45% in 2007 to between 9% and 50% in 2017. Furthermore, the average real and salaried remuneration also showed an increasing trend during the same period, while the average labor content per unit of output fell.
Crucially, the wage share of the economy during 2007-2017 is fundamentally explained by changes in the production structure, with changes in sectoral wage shares having little explanatory power. This applies both upward and downward, highlighting the importance of structural heterogeneity in explaining the evolution of the average wage share. On the other hand, the increased wage share in GDP during the final decade can be explained primarily by the increase in average real wages and salaried workers; additionally, the negative impact of the reduction in labor content per unit of output is also significant.
The technical coefficients of the 2017 IO matrix and an ad hoc model were used to establish four passive scenarios of final demand and changes in the different components of added value up to 2030. Passive projections from 1950-2017 and 1990-2017 data were used for the various components of final demand. Regarding the value-added components, the share of wages and salaries in the GVP of the 14 productive sectors analyzed was projected based on the 2007-2017 trend, and the corresponding adjustments were made to the primary input matrix.
The four scenarios incorporating predicted final demand - intersectoral relations, wage evolution, productivity, and labor content per unit of output (sectoral technical change) - predict a slight downward trend for the economy's wage share. Paradoxically, the most negative trend was the one related to the simple projection of the components of aggregate demand for the period 1950-2017; while the least negative was the one that incorporates the projection of demand for the period 1990-2017 and the new added-value structure. An intermediate situation would be the 1950-2017 trend with the new added-value structure and the 1990-2017 aggregate demand trend. These results are interesting in reflecting the direct and indirect impacts, which are identified through the use of the input-output matrix model.
Although the passive projections based on the structure and trends of the production structure on the wage share in output predict a downward trend towards 2030, the other explanatory variables discussed at the beginning of this article have the potential to positively or negatively impact this trend. Variables which could have a positive effect are the remuneration policies, income policies, and policies which promote workers’ collective bargaining rights (Jaumotte and Osorio, 2014). Variables which could have a negative impact, meanwhile, include the greater share of profits in the product, if the international prices of raw materials that are exported rise; higher concentration of ownership due to corporate mergers and acquisitions (Alarco, 2019); and intensified process of local and international financialization (Ostry et al., 2019).
The impacts of particular compositions of foreign trade, public spending, the new tax and fiscal policies, the exchange rate policy, to name just a few, have yet to be understood. On the other hand, empirical evidence from Latin America and Peru suggests that one of the greatest reducers of the wage share in GDP are the conventional economic adjustment and stabilization programs. Latin America must do everything possible to avoid macroeconomic imbalances that lead to the implementation of these standard responses.
Structural heterogeneity and the trends of shifts in technological change and demand combine to produce a lower wage share of output. A lower wage share, therefore, would tend to have a negative impact on personal income distribution. The accelerated technological change due to the COVID-19 pandemic driving a lower labor content per unit of output, however, has not been factored into this equation. There is some empirical data on this subject, such as Chernoff and Warman (2020), the International Federation of Robotics ([Federación Internacional de Robótica], 2021) and Acemoglu et al. (2021). Reducing high levels of inequality would require actions on the side of the productive structure, by promoting those sectors with a higher wage share or increasing productivity to reduce dispersion and to contribute to greater real wages, especially in low-productivity sectors. This goal should be achieved via a productive diversification strategy made viable via an industrial policy, going beyond social policy alone. Concrete proposals on this issue, however, have yet to be formulated and thus constitute a challenge for future research.
ACKNOWLEDGEMENTS
The author is grateful for the support of Martin Astocondor, as principal research assistant, as well as Toribio (Bikut) Sanchium. The valuable comments of Patricia del Hierro and the anonymous reviewers are also gratefully acknowledged. The author is solely responsible for the final version of this article.
REFERENCES
Acemoglu, D., Autor, D., Hazell, J. y Restrepo, P. (2021). AI and jobs: evidence from online vacancies. (Working Paper No. 28257). NBER. http://www.nber.org/papers/w28257. [ Links ]
Alarco, G. (2019). El impacto de las fusiones y adquisiciones en la distribución del ingreso y el PIB: América Latina, 1990-2014. Investigación Económica, 78(307 ).http://www.scielo.org.mx/pdf/ineco/v78n307/0185-1667-ineco-78-307-54.pdf. [ Links ]
Alarco, G. y Castillo, C. (2018). Distribución factorial del ingreso y régimen de crecimiento en el Perú, 1942-2013. Revista CEPAL, 125. https://www.cepal.org/es/publicaciones/43998-distribucion-factorial-ingreso-regimen-crecimiento-peru-1942-2013. [ Links ]
Alarco, G., Castillo, C. y Leiva, F. (2019). Riqueza y desigualdad en el Perú, visión panorámica. Oxfam. [ Links ]
Aroche, F. (2019). Estructura productiva y crecimiento económico en México: una perspectiva multisectorial. Investigación Económica, 78(309 ).http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0185-16672019000300003. [ Links ]
Aroche, F. y Márquez, M. (2013). The demand-drivern and the supply-sided input-output. Notes for the debate. MPRA Paper No. 61132. https://mpra.ub.uni-muenchen.de/61132/. [ Links ]
Banco Central de Reserva del Perú (BCRP) (1970). Cuentas Nacionales del Perú 1960-1969. BCRP. [ Links ]
Chernoff, A. y Warman, C. (2020). Covid-19 and implications for automation (Working Paper No. 27249). NBER. http://www.nber.org/papers/w27249. [ Links ]
Federación Internacional de Robótica (2021). US robot density in car industry ranks 7th worldwide. https://ifr.org/ifr-press-releases/news/us-robotdensity-in-car-industry-ranks-7th-worldwide. [ Links ]
Ffrench-Davis, R. (2019). Oswaldo Sunkel y el desarrollo o crecimiento incluyente. En A. Bárcena y M. Torres (eds.). Del estructuralismo al neo-estructuralismo, la travesía intelectual de Oswaldo Sunkel (pp. 59-75). Naciones Unidas. https://repositorio.cepal.org/bitstream/handle/11362/44710/1/S1701115_es.pdf. [ Links ]
Gonzáles de Olarte, E. (2015). Una economía incompleta 1950-2007: análisis estructural. Fondo Editorial de la PUCP. [ Links ]
Infante, R. (2007). Una política de distribución de ingresos desde la perspectiva de la heterogeneidad estructural. En M. Jélvez (ed.). Perspectiva Económicas para el Chile del Bicentenario: Desafíos y Oportunidades (pp. 81-111). PNUD. [ Links ]
Infante, R. y Sunkel, O. (2009). Hacia un desarrollo inclusivo, el caso Chile. Revista CEPAL, 97. https://www.cepal.org/es/publicaciones/1384-un-desarrollo-inclusivo-caso-chile. [ Links ]
Instituto Nacional de Estadística e Informática (INEI) (1990). Cuentas Nacionales del Perú 1981-1990. INEI. [ Links ]
______(1991). Cuentas Nacionales tablas insumo-producto 1990. INEI. [ Links ]
______(1992). Cuentas Nacionales tablas insumo-producto 1991. INEI. [ Links ]
______(2000). Tabla insumo producto de la economía peruana 1994. INEI. [ Links ]
______(2019). Cuentas Nacionales del Perú 1950-2017. INEI. [ Links ]
Jaumotte, F. y Osorio, C. (2014). Inequality and labor market institutions (IMF Staff Discussion Note, SDN/15/14). FMI. [ Links ]
Kalecki, M. (1956). Teoría de la dinámica económica: ensayo sobre los movimientos cíclicos y a largo plazo de la economía capitalista. Fondo de Cultura Económica. [ Links ]
Kozikowski, Z. (1988). Técnicas de planificación macroeconómica. Editorial Trillas. [ Links ]
Lindenboim, J., Kennedy, D. y Graña, J. (2011). Distribución funcional y demanda agregada en Argentina. Sesenta años en perspectiva internacional. Instituto de Investigaciones Económicas de la Facultad de Ciencias Económicas, Universidad de Buenos Aires y CEPED. [ Links ]
Ostry, J., Loungani, P. y Berg, A. (2019). Confronting inequality, how societies can choose inclusive growth. Columbia University Press. [ Links ]
Pinto, A. (1970). Naturaleza e implicaciones de la heterogeneidad estructural de América Latina. El Trimestre Económico, 37(1).https://repositorio.cepal.org/handle/11362/2055. [ Links ]
Quaresma de Araujo, P. (2013). Estructura productiva y distribución funcional del ingreso: una aplicación del modelo insumo-producto. Revista CEPAL, 129. https://www.cepal.org/es/hojasinformativas/estructura-productiva-distribucion-funcional-ingreso-aplicacion-modelo-insumo. [ Links ]
Távara, J., Gonzáles de Olarte, E. y Del Pozo, J. (2014). Heterogeneidad estructural y articulación productiva en el Perú. En R. Infante y J. Chacaltana (eds.). Hacia un desarrollo inclusivo. El caso del Perú (pp. 39-79). CEPAL-OIT. [ Links ]
Torres, M. (2019). Globalización, capitalismo transnacional y dependencia: el itinerario de una visión. En A. Bárcena y M. Torres (eds.). Del estructuralismo al neoestructuralismo, la travesía intelectual de Oswaldo Sunkel (pp. 137-195). Naciones Unidas. https://repositorio.cepal.org/bitstream/handle/11362/44710/1/S1701115_es.pdf. [ Links ]
1These authors argue that social policy carries risks and is not itself sufficient to reduce inequalities, given that it depends on the fiscal situation; second, the standard of living of poor families would depend less on labor income.
2The matrices prepared by the BCRP are compact and omitted wages and salaries for government activity in 1950, 1955, 1956, and 1961. In light of this, the present article assumes that 95% of the value added is allocated to wages and salaries, as observed in the closest input-output table for 1973. Regarding “miscellaneous” activity, which did not have this data for 1950, the 1955 percentage structure was used even though it was biased in favor of gross operating surplus.
3Between 2010 and 2011, the observed wage share of GDP decreased due to the increased gross operating surplus resulting from higher international commodity prices that increased the mining sector’s contribution to output. A more extensive explanation can be found in Alarco and Castillo (2018).
4Unfortunately, it is not possible to use information prior to 2007, as the classification criteria for sectoral data are different for both GVP and employment.
5This trend can be observed in each of the 14 economic activities. Declines in real wages are also recorded in fisheries and aquaculture, financial services, insurance and pensions, and, more recently, construction.
6In the case of a function of the type Z = xy the total differential in discrete terms is equivalent to ΔΖ = Δxγ + Δγx + ΔxΔγ . When the function has three components the total differential in discrete terms is equivalent to ΔΑ = γzΔx + xzΔγ + xγΔz + zΔxΔγ + γΔxΔz + xΔγΔz + ΔxΔγΔz.
7It should be noted that when the share of total wages and salaries is reduced, and the explanatory factor assumes a negative value, the explanation is that it contributes positively to the reduction in the share of wages and salaries.
8An updated but brief explanation of the model’s operation and main assumptions can be found in Aroche (2019), while a more extensive one can be found in Aroche and Márquez (2013), which includes a discussion of the questioned operation of the IO on the supply side.
9In all cases of the final demand components except for the trend of exports 1990-2017, the polynomial of degree three Y=a+bt+ct2+dt3 was selected as the best equation. In the case of 1990-2017 exports, a regression of type Y=a+bt2+ct3 was chosen, given that the traditional cubic form generated decreasing projections from the mid-2020s onwards.
10In all cases the regression for sectoral wage shares was of the Ln V=a+b t type. Likewise, for the 2018-2030 projections only the average annual growth rate b*100 was considered.
ANNEX.INPUT-OUTPUT MATRIX OF THE PERUVIAN ECONOMY, 2017
Final demand matrix (D)
| Final household consumption | Final government consumption | GFCF | Export. | EV |
| 0.0595 | 0.0000 | 0.0156 | 0.0642 | 2.1316 |
| 0.0071 | 0.0000 | 0.0000 | 0.0001 | 0.0000 |
| 0.0000 | 0.0000 | 0.0112 | 0.5287 | 1.9494 |
| 0.3700 | 0.0023 | 0.3213 | 0.3510 | -3.3949 |
| 0.0241 | 0.0000 | 0.0000 | 0.0002 | 0.0000 |
| 0.0008 | 0.0000 | 0.6366 | 0.0000 | 0.3076 |
| 0.0067 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0986 | 0.0000 | 0.0000 | 0.0401 | 0.0000 |
| 0.1232 | 0.0000 | 0.0000 | 0.0346 | 0.0000 |
| 0.0509 | 0.0005 | 0.0064 | 0.0043 | 0.0063 |
| 0.0483 | 0.0028 | 0.0000 | 0.0014 | 0.0000 |
| 0.0073 | 0.0000 | 0.0062 | 0.0151 | 0.0000 |
| 0.0027 | 0.6023 | 0.0000 | 0.0000 | 0.0000 |
| 0.2009 | 0.3921 | 0.0027 | 0.0084 | 0.0000 |
Matrix of technical coefficients of national inputs (A)
| 1 | Agriculture, livestock, hunting, and forestry | 0.1245 | 0.0009 | 0.0000 | 0.1340 | 0.0000 | 0.0001 | 0.0002 | 0.0000 | 0.0647 | 0.0000 | 0.0000 | 0.0000 | 0.0019 | 0.0009 |
| 2 | Fishing and aquaculture products | 0.0000 | 0.0106 | 0.0000 | 0.0133 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0065 | 0.0000 | 0.0000 | 0.0000 | 0.0005 | 0.0000 |
| 3 | Oil, gas, minerals, and related services | 0.0012 | 0.0000 | 0.0486 | 0.0902 | 0.0441 | 0.0375 | 0.0000 | 0.0001 | 0.0002 | 0.0000 | 0.0000 | 0.0000 | 0.0043 | 0.0004 |
| 4 | Manufactured products | 0.1102 | 0.2478 | 0.1384 | 0.3286 | 0.0766 | 0.3655 | 0.0659 | 0.2248 | 0.3295 | 0.1107 | 0.0323 | 0.0852 | 0.1599 | 0.0906 |
| 5 | Electricity, gas, and water services | 0.0019 | 0.0126 | 0.0294 | 0.0210 | 0.1394 | 0.0006 | 0.0137 | 0.0115 | 0.0076 | 0.0101 | 0.0069 | 0.0056 | 0.0173 | 0.0104 |
| 6 | Construction | 0.0000 | 0.0000 | 0.0044 | 0.0006 | 0.0079 | 0.0174 | 0.0005 | 0.0000 | 0.0001 | 0.0059 | 0.0035 | 0.0000 | 0.0324 | 0.0043 |
| 7 | Trade and vehicle maintenance and repair services. | 0.0001 | 0.0000 | 0.0036 | 0.0011 | 0.0034 | 0.0000 | 0.0025 | 0.0609 | 0.0002 | 0.0009 | 0.0004 | 0.0060 | 0.0143 | 0.0016 |
| 8 | Transportation, warehousing, storage, and mail and courier services | 0.0149 | 0.0134 | 0.0790 | 0.0212 | 0.0424 | 0.0086 | 0.1183 | 0.1393 | 0.0074 | 0.0180 | 0.0182 | 0.0187 | 0.0318 | 0.0110 |
| 9 | Accommodation and restaurants | 0.0000 | 0.0000 | 0.0020 | 0.0009 | 0.0038 | 0.0004 | 0.0106 | 0.0081 | 0.0008 | 0.0063 | 0.0016 | 0.0113 | 0.0206 | 0.0060 |
| 10 | Telecommunications and other information. | 0.0000 | 0.0022 | 0.0015 | 0.0018 | 0.0022 | 0.0010 | 0.0125 | 0.0034 | 0.0086 | 0.1557 | 0.0404 | 0.0799 | 0.0129 | 0.0111 |
| 11 | Financial services, insurance, and pensions | 0.0074 | 0.0422 | 0.0324 | 0.0180 | 0.0370 | 0.0114 | 0.0558 | 0.0205 | 0.0135 | 0.0352 | 0.1052 | 0.0244 | 0.0476 | 0.0154 |
| 12 | Business services | 0.0147 | 0.0078 | 0.0364 | 0.0301 | 0.0271 | 0.0425 | 0.0573 | 0.0544 | 0.0149 | 0.2190 | 0.0931 | 0.1606 | 0.0619 | 0.0564 |
| 13 | Public administration and defense services | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 14 | Other services | 0.0004 | 0.0026 | 0.0021 | 0.0025 | 0.0024 | 0.0008 | 0.0214 | 0.0061 | 0.0135 | 0.0377 | 0.0313 | 0.0290 | 0.0039 | 0.0462 |
Primary input matrix (B)
| 1 | Worker remunerations | 0.1136 | 0.1397 | 0.1364 | 0.0959 | 0.1061 | 0.2062 | 0.1956 | 0.0884 | 0.1338 | 0.1220 | 0.2122 | 0.2233 | 0.4954 | 0.3616 |
| 2 | Other taxes | 0.0003 | 0.0046 | 0.0039 | 0.0040 | 0.0230 | 0.0014 | 0.0030 | 0.0090 | 0.0015 | 0.0133 | 0.0039 | 0.0034 | 0.0002 | 0.0028 |
| 3 | Gross operating surplus | 0.0383 | 0.3255 | 0.4648 | 0.1823 | 0.4753 | 0.2097 | 0.1867 | 0.1284 | 0.1051 | 0.2344 | 0.4484 | 0.2035 | 0.0951 | 0.2786 |
| 4 | Mixed income | 0.5726 | 0.1900 | 0.0170 | 0.0546 | 0.0095 | 0.0970 | 0.2560 | 0.2452 | 0.2921 | 0.0307 | 0.0025 | 0.1491 | 0.0000 | 0.1026 |
Matrix (Z)
| Final household consumption | 440 144 |
| Final government consumption | 93 242 |
| GFCF | 141 239 |
| Exports | 168 816 |
| EV | 790 |
Source: Compiled by the authors using data from INEI (2019).
Received: April 21, 2021; Accepted: October 28, 2021











 texto en
texto en 


