Study area

The study area was Forest Management Unit 1205 (UMAFOR-1205), which is located within the Sierra Madre del Sur mountain system in the central region of the state of Guerrero (Figure 1).

Figure 1 Location of the study area. 

Climate types in coniferous forest areas vary from temperate to semi-warm with different humidity graduations. However, the predominant type of climate is (A) C _(w) (^{García, 2004}).

Soils are classified as Leptosols, Luvisols, Regosols and Cambisols, of which Leptosols have the highest distribution within the study area (^{Inegi, 2016}).

Sampling

The selective sampling method was applied in the low, medium and high season qualities of UMAFOR-1205 to collect 27 dominant trees and 28 codominant trees, without physical damage, with ages from 20 to 100 years. Slices were obtained from the stem of each tree at 0.30 m, 0.60 m and 1.30 m high and subsequently at every 2.60 m until reaching the tip to reconstruct 102 and 152 profiles of Pinus pseudostrobus and Pinus oocarpa trees, respectively, starting from the collected trees and applying the methodology to perform the trunk analysis described by ^{Klepac (1983)}.

Variables

The initial measurements that were taken per tree of each species were normal diameter with bark obtained at 1.30 m height with a 283D Lufking^TM 5M diametric tape; barkless diameter of each slice measured with a Lufking^TM rule and estimated as the average of two measurements taken in the cross. The rings from each slice were divided into groups of ten to measure radial growth at different heights. The age of each of the reconstructed trees was determined on the largest diameter of the slice obtained at 30 cm high of the stem. To measure the normal diameter and estimate the basimetric area of each reconstructed tree, growth rings were grouped in ages of 10 years from the center to the periphery (^{Klepac, 1983}). The estimation of the true height was carried out using the ^{Carmean (1972)} formula modified by ^{Newberry (1991)}, whose expression is:

Where:

Hij = Estimated total height in the i- ^th slice, corresponding to j growth rings

hi  = Cumulative height to top cut of each i -^th slice

hi+1= Cumulative height to top cut of each next i -^th slice

ri = Number of growth rings of the i -^th slice

ri+1 = Number of growth rings of the next i -^th slice

j = Number of growth rings from the core of each slice

The basimetric area was determined by the following equation:

Where:

AB = Basimetric area

π =3.14159

dn = Normal diameter measured at 1.30 high from the surface of the ground

The volumes of each log were estimated with the Smalian equation and that of the cone, respectively.

Where:

DM= Largest diameter of each log

Dm = Smallest diameter of each log

Db= Diameter at the base of the tip (m)

l = Log’s length (m)

The sum of the volumes of the logs of each tree was equal to the total volume without bark of the stem.

Table 1 shows the basic descriptive statistics of the variables analyzed by species.

Analysis

To the growth data in normal diameter, basal area, height and volume, the growth models of Chapman-Richards (M1), Hossfeld I (M2), Weibull (M3) and Schumacher I (M4) mentioned by ^{Kiviste et al., (2002)} using nonlinear regression (Table 2). In addition, their respective expressions were generated to determine the annual current increase (ICA, for its acronym in Spanish) and the average annual increase (IMA, for its acronym in Spanish). The adjustments were made by applying the PROC MODEL procedure of the SAS statistical program (^{SAS, 2002}). The analytical criterion to select the goodness of fit of the models considered the root mean square error (REMC), the adjusted coefficient of determination (R ² _adj ) and the statistical properties of the estimated parameters.

Where:

yi, y^i, y-i = Valor observado y valor predicho i de cada variable, así como el promedio estimado de la variable observadan = Number of observations

p = Number of the parameters of the mode

Finally, as a determining factor to select the best model, the graphical analysis of the growth curves was considered.

Since the growth measurements over time of each assessed variable within each tree are correlated, the significance of the autocorrelation of the selected models was evaluated as the best using the Durbin-Watson (DW) test (^{Sharma et al., 2011}; ^{Quiñonez et al., 2018}).

Where:

et = t residual of each observation

et-1 = residual of each observation before the et residual

When this test was significant, the CAR (X) autoregressive model (^{Zimmerman et al., 2001}) was applied to correct the autocorrelation problem and generate parameters and standard errors consistent with the models. The structure of the autoregressive model is:

Where:

eij = j-th ordinary residual in observation i

Ik = 1 for j >k and 0 for j=k (k=1, 2, 3,…, x)

ρk = Autoregressive parameter of the k order

 hij-hij-k, = Separation distances of the j^th to the j-k ésim observation

εij = Independent error that follows a normal distribution with zero mean and constant variance

Once the best model was selected, the maximum ICA (ICA _máx ) and maximum IMA (IMA _máx ) were estimated for each of the variables and species. Both increases correspond to the highest values estimated with the ICA and IMA equations.

Goodness of fit of models

The R ² _adj and RCME statistics indicated that in Pinus pseudostrobus, the Weibull model was the one that best adjusted to estimate growth in diameter and volume and those of Chapman-Richard and Weibull in height; in turn, all models were adjusted in a similar way in estimating the basal area. In Pinus oocarpa, the Hossfeld I model was the one that registered the best fit in diameter, those of Chapman-Richard and Weibull in basimetric area, those of Schumacher and Weibull in height, as well as those of Chapman-Richard, Weibull and Schumacher in volume (Table 3).

However, when considering the level of significance of the parameter estimators (α <0.05), the Weibull model was rejected to predict growth in diameter, basimetric area, height and volume in Pinus pseudostrobus, and growth in basimetric area. and volume for Pinus oocarpa. In a similar way, the Chapman-Richards and Hossfeld I volume growth models showed non-significant parameters in Pinus pseudostrobus. For this species, only the Schumacher model recorded estimators of the significant parameters in the four growth variables studied. In relation to Pinus oocarpa, all the estimators of the Chapman-Richard, Hossfeld I and Schumacher models were significant (Pr <0.0001) in the four variables studied. Based on the previous context, the graphical assessment in the estimation of the growth of each variable by species carried out with the models whose parameters were all significant, allowed to define the best model.

Growth curve trends

Figure 2 shows that both the Chapman-Richards and Schumacher models predict very similar normal diameter growths for both species up to 50 and 65 years. From these ages, the growth rate predicted with the Chapman-Richards model tends to zero, while, with the Schumacher model, growth continues upward until reaching the asymptote. The maximum growth in diameter estimated with the Chapman-Richards model in Pinus pseudostrobus and Pinus oocarpa were lower than those predicted with the Schumacher model; the latter presented more plausible growth rates at ages over 60 years and was selected to make the predictions of the growth in diameter of both species.

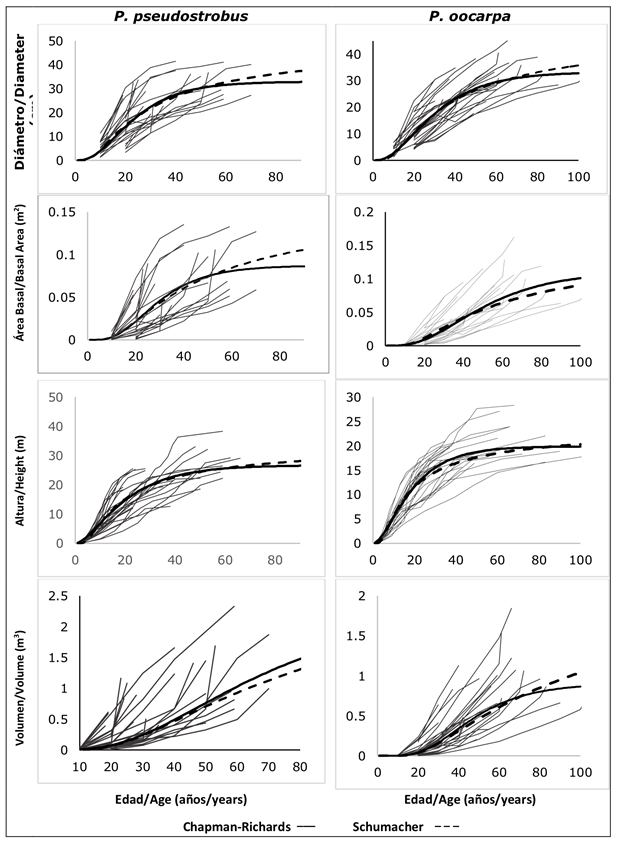
Figure 2 Comparison of the trends of the growth curves generated by the Schumacher and Chapman-Richards models with respect to the growth series observed for the variables analyzed. 

In reference to the basimetric area, the Schumacher model was the one that best showed the trend in Pinus pseudostrobus, while the Chapman-Richards model did so in Pinus oocarpa during the evaluated period. In the first species, the Schumacher model predicted minor growths in the basimetric area up to an approximate age of 70 years, while in Pinus oocarpa, the same happens over the entire growth period evaluated.

In the graphical analysis of the growth in total height, the Schumacher model is the one that best predicts this growth. The Hossfeld I model exhibits a higher growth rate after 40 years in Pinus pseudostrobus and after 60 years in Pinus oocarpa, while the Chapman-Richards and Weibull models decrease it drastically after 50 years, and showed the asymptotes at an early age.

On the other hand, the predictions of volume growth with the Schumacher model in Pinus pseudostrobus and Pinus oocarpa are lower than those calculated with the Chapman-Richards model throughout the evaluation period, in which the intermediate fellings are programmed, Therefore, if it is desired to avoid overestimating the usable volume, the Schumacher model is considered the most appropriate for such predictions. In turn, the Chapman-Richards model presents the asymptote after 60 years of age, and reflects the lower estimates after that age.

Maximum Annual and Shift Current Increases

The estimates made with the equation derived from the Schumacher normal diameter growth model indicated that the ICA _máx in diameter in Pinus pseudostrobus and Pinus oocarpa were recorded at 12 (1.09 cm) and 15 years (0.86 cm), while those in the area baseline predicted with the equation derived from the Chapman-Richards model were obtained at 30 and 37 years (0.0017 cm), respectively. The ICA _máx in total height determined with the equation derived from the Schumacher model occurred at 8 (1.15 m) and 7 years (0.90 m). In turn, the ICA _máx in stem volume predicted with the equations derived from the Chapman-Richards and Schumacher models were apparent at 38 (0.024 m³) and 41 years old (0.018 m³) in Pinus oocarpa and Pinus pseudostrobus, respectively. The age of the physical shift of the volume estimated with the Schumacher equation was determined at 82 years in Pinus pseudostrobus and 62 years in Pinus oocarpa (Figure 3).

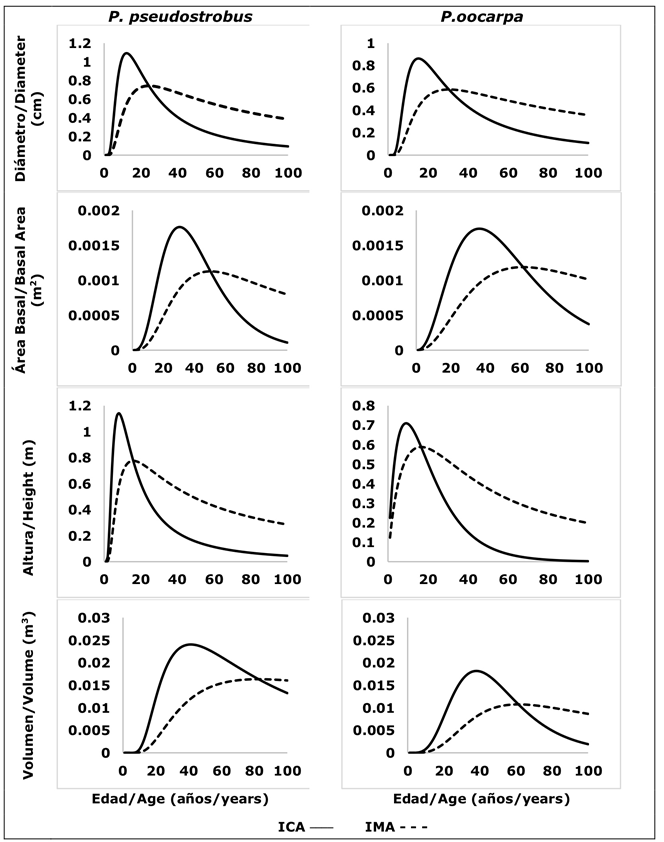
Figure 3 Trends of the ICA-IMA curves generated by the evaluated models in relation to the growth series. 

If both species are associated in the same type of forest, the difference in growth patterns, the time in which the maximum increases are recorded and the turn, it is possible to assume that these species respond differently to the same environmental conditions and levels. productivity prevailing in this ecosystem. The growth predictions made with the selected models suggest that the Pinus pseudostrobus individuals reached greater dimensions in diameter, height and volume than those of Pinus oocarpa during the studied period.