1 . Introduction
Mass is a physical quantity -like length, charge, or volume- associated with a class of determinate mass magnitudes (which we denote in various ways: ‘2kg’, ‘4.7g’, ‘the mass of this pumpkin’, etc.). Mass also has “quantitative structure”, which is to say that mass magnitudes stand in certain structuring relations which we commonly represent with bits of mathematics. The relations relevant here are illustrated thusly: 2kg is “less than” 4kg (mass ordering). 12g is the “sum of” 5g and 7g (mass summation). 14.6kg is 2.5-times greater than 5.84kg (mass ratio).1
The goal of a theory of mass is to be able to explain physical phenomena involving that quantity, and properly characterize the role of mass in bringing about those phenomena. There are two such phenomena central to mass’s role in most physical theories. The first, mass’s additivity, concerns how the masses of some bodies determine the masses of others, specifically of objects those bodies compose. This is contrasted with the second, mass dynamics -the dynamics of massive bodies- which concerns how (given the dynamical laws) the mass of an object determines the values of other quantities, like the distance between two bodies after a given amount of time, or the degree to which a particle accelerates after being impressed by some force. In this paper, I’ll present a powerful objection to any view according to which the first of these phenomena is metaphysically independent of the second.2
The objection extends, I argue, to views which take mass summation (the aspect of mass’s quantitative structure) to be metaphysically independent of its dynamics. Mass summation is distinct from mass additivity. Mass additivity concerns what mass properties certain mereological sums will instantiate, given the masses of their parts. It is silent on which determinate mass magnitudes are the “sums” of which other mass magnitudes. In contrast, mass summation structure is silent on which mass properties are to be instantiated in the world, but it does determine which of those mass properties are the “sums” of which other ones. While mass additivity has not been the subject of very much attention in philosophy, mass summation plays an extremely important role in many theories of quantity -including both those views in the tradition of Hölder (1901) , two influential contemporary examples being those defended by Brent Mundy (1987) and Maya Eddon (2013b), as well as the magnitude realism of Peacocke (2019).
1 . 1 . Two Physical Phenomena Involving Mass
Before I go on, let’s get a clearer picture of the two phenomena3 I’m interested in, and the role mass plays in bringing them about:
Mass Additivity. The masses of physical objects “add up” when taken together to form a whole. So, if Pumpkin weighs 98kg and Wheelbarrow 21kg, then the whole, Pumpkin-in-Wheelbarrow, will have a mass of 119kg (where 98 + 21 = 119 or, more importantly, 119kg is the “sum” of the mass magnitudes 98kg and 21kg). More generally, massive bodies, and the objects they compose, obey the following bridge law.
(ADD-BRIDGE) If x and y are massive, don’t overlap, and compose z, then (i) z is massive, and (ii) z’s mass is the sum of x’s mass and y’s mass.
Mass Dynamics. The second phenomenon concerns mass’s role in determining how massive bodies move around, and how systems of those bodies evolve through time, in accordance with the dynamical laws. In classical mechanics, mass is closely associated with an object’s inertia (the degree to which it resists change in its state of motion due to outside forces) and the gravitational pull an object has on other massive bodies (and that other bodies have on it). Here the quantitative structure of mass will be tied, via the laws, to certain behaviors -e.g., acceleration of massive bodies after a collision, the gravitational attraction of the earth on the apple in my hand, the amount of force required to push my laptop off of my desk, etc.
1 . 2 . Sketch of the Paper
I will make my argument first by considering the question: Is there anything more to additivity than dynamics? Do we need, that is, to posit a bridge law like (ADD-BRIDGE), as some kind of fundamental principle, in order to adequately capture and explain the way massive objects move around in accordance with the laws? Conversely, is explaining dynamics sufficient to explain mass additivity (and everything that comes with it) or do we need to posit something more -viz. something along the lines of (ADD-BRIDGE)- for our view to adequately account for it?
In what follows, I make the case against mass additivity being metaphysically independent of mass dynamics (i.e., I make the case that mass additivity is either dependent on dynamics or there is, at least strictly speaking, no such thing). Here’s how I do that: In section 2, I argue that, on certain physical pictures (specifically Newtonian Particle Mechanics), mass additivity is not necessary to properly capture the dynamics of simple massive particles (or, more importantly, mass’s role in that dynamics). In contrast, the dynamics of massive particles, together with the mass ratio relations, is sufficient to derive an approximation that adequately captures what I call “the physical significance” of mass additivity.
In section 3, I argue that the results of section 2 imply that any theory which accepts fundamental mass additivity is committed to a pervasive explanatory failure. Specifically, theories committed to fundamental additivity cannot explain the close correspondence (out-lined in section 2) between the dynamic behavior of massive simples and the assignment of mass properties to the objects those simples compose (as determined by (ADD-BRIDGE) or a similar fundamental principle). I refer to these kinds of widespread systematic coincidences or correlations between distinct phenomena as ‘unexplained choreography’, since it involves distinct elements of the theory “marching in lockstep” with no apparent mechanism for their collusion.
The second half of the paper extends this explanatory worry, arguing that the very same considerations apply to certain aspects of mass’s quantitative structure, namely its summation structure -facts about which mass magnitudes are the “sums” of which others. This is significant, since, while most accounts of mass are silent on the metaphysical status of additivity, a great many of them rely heavily on taking as fundamental some of mass’s sub-metrical structure, like mass summation. Most notably: The views defended by Mundy (1987) and Eddon (2013a) (as well as other views following the approach to quantity pioneered by Hölder (1901)) take mass magnitudes to be universal properties and posit fundamental second-order relations distributed over these properties, including a relation of mass ordering and of mass summation, and then ground mass ratios via a representation and uniqueness theorem. Likewise, the magnitude realism of Peacocke (2019 and 2015) also treats the summation structure of extensive magnitudes as fundamental (or at least as fundamental as anything about a given quantity), using it to characterize other quantitative structure (like ratios).
However, there is an asymmetry between this and the previous explanatory worry, since those same views use fundamental mass summation structure to ground mass ratios which (by the arguments in section 2) do play a role in explaining the dynamics. In section 4, I show that even though, on such views, mass summation (via the mass ratios) partially explains the dynamics, these views still cannot explain the systematic correspondence between features of the fundamental summation facts and the dynamic behavior of massive bodies. This is because mass ratios explain dynamics in a way that’s insensitive to their grounds (and, so, do not make any different an explanatory contribution to dynamics when they’re grounded by fundamental summation structure versus any other candidate grounds of mass ratios).
In the final section, I consider the broader implications of these worries and gesture at a way their morals could inform a positive account of mass’s quantitative structure. I also examine the metaphysics of other additive quantities (like length, charge, or volume) would be susceptible to this same line of argument.
2 . Additivity from Dynamics
In this section, I argue that (at least in the case of Newtonian Particle Mechanics) mass additivity, via a bridge law like (ADD-BRIDGE), is not necessary to adequately account for or explain the dynamics of massive bodies -even dynamics closely associated with mass additivity, like the motions of composite objects. In contrast, I will argue, the dynamics of massive simples, without appeal to additivity (and, so, without any assignment of masses to composite objects), is sufficient to define a close approximation of additivity. Specifically, I argue that the dynamics of massive simples is able to fully capture what I call the “physical significance” of mass additivity.
(For this section and remainder of this article, I restrict my discussion and examples to Newtonian Particle Mechanics: A 4D Euclidean spacetime occupied by massive point particles whose trajectories are governed by F = ma -with or without gravitation, described by force law:
2 . 1 . Additivity is Not Necessary for Dynamics
In Newtonian Particle Mechanics, the motion of simple particles is determined by their masses, together with the mass ratios between them (and the non-mass facts, like relative velocities, etc.). Since the positions and motions of composite objects is nothing over and above the position and motion of their parts, those same mass ratios determine their motions as well. More accurately, the masses of, and ratio relations between, simple particles determine the absolute change in motion (acceleration) of those particles. For a given pair of particles, the difference in their rates of acceleration under the same conditions is determined by their respective masses and mass ratio.5
I won’t give a rigorous argument for this, I’ll just point to two relevant examples, and show that metrical mass facts are sufficient to ground mass’s contribution to this behavior, according to the laws. The first example is elastic collision between two massive bodies: Suppose two particles, with respective masses of m
1 and m
2, collide head on. By Newton’s third law, they are subject to forces of equal strength but in opposing directions. Since F = ma and each particle is under a force of equal strength, the differences in their accelerations will be determined by their masses. Specifically:
The second example is gravitational attraction between two massive bodies as determined by the force law
where r is the distance between the two massive bodies and G is the gravitational constant. Here the strength of the gravitational attraction is proportional to each particle’s mass. When determining the acceleration of the first particle using
Similarly for the second particle’s acceleration. This means that, if we took the ratio between the two particles’ accelerations,
There’s an important property of these cases which will be relevant to the next argument: Without (ADD-BRIDGE), objects composed out of two or more massive particles do not have mass properties of their own and, so, do not stand in mass ratio relations. However, in a theory like Newtonian Particle Dynamics,6 the mass ratios between composite bodies are not necessary to account for their dynamic behavior. Once the dynamics of simple bodies (particles) is determined, the dynamics of composite bodies “falls out”, so to speak (indeed, it would have to be this way. What possibly could be left undetermined about the location of the whole once we’ve specified the location of its parts?).7
2 . 2 . Dynamics is Sufficient to Approximate Additivity
The previous argument establishes that the dynamics of massive bodies in Newtonian Particle Mechanics need not depend on mass additivity. I’ll now argue that the dynamical laws, plus the masses of and mass ratios between simples, are sufficient to determine approximate additivity. Recall that additivity concerns how the masses of some bodies determine the masses of others -viz. the ones they compose. This is what I called, earlier, the “physical significance” of additivity. What the dynamics gives us falls short of this, since mass’s dynamics will not (on most accounts) entail that composite objects literally instantiate magnitudes of mass just because their parts do. However, if we consider, instead, the physical upshot of ascribing a mass to a body -what such an ascription encodes about its law-governed behavior and its relationship to other parts of our physical theory- we’ll see that a composite object does exhibit (approximately) the sort of physical behavior and dispositions characteristic of a body possessing that particular mass. The dynamic behavior of simples, then, gives us a handle on the physical significance of ascribing mass to a composite which, thereby, captures the physical significance of additivity in the first place.
There’s just one hiccup. Standard textbook presentations of the dynamics for a composite body usually start by treating it as if it were a simple body whose mass is the “sum” of the masses of its simple parts, and which is typically located at their center of mass. And, while there are some presentations that do not treat additivity as a given, and try to show how it can be derived from dynamics, they won’t do for our purposes. Kibble and Berkshire’s Classical Mechanics(2004) offers a kind of reduction of additivity to dynamics for the specific cases where the bodies are bound together into a rigid body, which is similar to the illustration I offer in section 2.4. Both are limited only to a certain class of composites (those which are bound together into a single, more-or-less rigid, body). Feather (1966) attempts to give a more general kind of derivation, but his account is built around the standard procedure for determining the center of mass, which relies on appeal to the “sum” of their masses (as well as requiring that we assign coordinates to each particle’s position in space).8
First, I’ll show that we do not need (ADD-BRIDGE) (nor even direct appeal to summation structure) applied to the masses of each particle in a system, to determine their center of mass. Then, I’ll outline a way we can use just the masses of simple particles and their mass ratios to determine a composite body’s dynamics directly, without appeal to its center of mass, by assuming it is a rigid body.
2 . 3 . Center of Mass
Attempts to explain mass’s additivity in terms of its dynamics often proceed via the definition of the center of mass. Feather’s (1966) attempt to define additivity in a general way, without relying on any features unique to particles that compose a rigid body, is the most notable example.
The standard procedure for determining center of mass, for a system of n particles, depends explicitly on “summing up” those particles’ masses. It also depends on a choice of Cartesian coordinates, and determines the x, y, and z coordinates of the center of mass independently, via an instance of the equation9 (where ‘X CoM’ is the X coordinate of the center of mass, and ‘m i ’ and ‘x i ’ the mass and x coordinate of the i’th particle in the system, respectively),
McQueen (2015) has objected that Feather’s account, and others that rely on appeal to the center of mass, suffer from several weaknesses. The more significant of them, according to McQueen, is that any account making use of standard definitions of the center of mass of a system commit themselves to a vicious circularity. They must appeal to the sum of the masses of those particles (the value m 1 + · · · + m n , above) in order to determine the correct position of the center of mass. If we did not already know this value, then there would not be a way to find the position of the center, and so we could not use the dynamical behavior of that center to determine what mass to assign it. While this isn’t quite the same thing as making use of (ADD-BRIDGE), it comes dangerously close, and (more importantly) my arguments are supposed to extend to mass summation structure in general, so we should do without it if we can.
McQueen’s solution is to consider a range of slight variations on Feather’s picture, each which assigns a slightly different mass value to the mereological sum of a system of massive particles, and then argue that, among these candidates, only the one which assigns the “correct” value is the most “natural” (in a Lewisian sense) candidate law. While I agree with some of McQueen’s criticisms of Feather, I cannot accept his proposed solution. Luckily we don’t need anything so metaphysically weighty as relative naturalness to solve these problems. In fact, neither equation (4) nor any other appeal to the “sum” of these particles’ masses is necessary to determine the position of their center of mass. All we need are the mass ratios and the ratio structure of length (as well as a little geometry). Let’s get started:
Center of Mass without Mass Summation
It should be obvious that, when two bodies, α and β, are equal in mass, their center of mass, ‘x’, must be the point equidistant between them, i.e., must sit on the midpoint of the line αβ. If you make α a bit more massive, x moves a bit closer to α along αβ (see Figure 1). Indeed, it’s not hard to see that the length ratio between the lines αx and xβ must be the inverse of the mass ratio between α and β. If β is 3/2 times as massive as α, the shortest path from β to x should be 2/3-times as long as the shortest path from x to α.
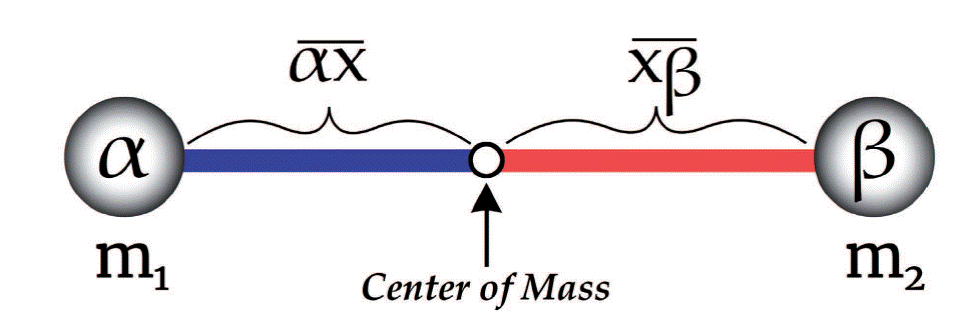
Figure 1: Center of Mass for two particles. The length ratio between αx and xβ is the same as the mass ratio between β and α (i.e., the inverse of the ratio between α and β).
Does this procedure generalize? The method for two particles extends very naturally to three: Consider again the equal-mass special case. The center of mass of a trio of (non-collinear) equal-massed particles, α, β, and γ is the point at the “middle” of the triangle that they form, which is also known as the “centroid”. A centroid is the point of intersection of the three medians of the triangle -the three lines that connect each vertex to the midpoint of the opposite side. So a straight line through α and the center of mass will intersect βγ at its midpoint. Of course, in the equal-mass case, the midpoint of βγ is also their (β and γ’s) center of mass. As it turns out, this fact holds for the non-equal case as well. The center of mass of three (non-collinear) points is their “Centr(of-mass)oid”, i.e., the point, c, within the triangle they form such that a straight line through each vertex/particle (e.g., α) and c will intersect the opposite edge of the triangle (βγ) at the center of mass of the two other vertices/particles (β and γ, as illustrated in Figure 2).
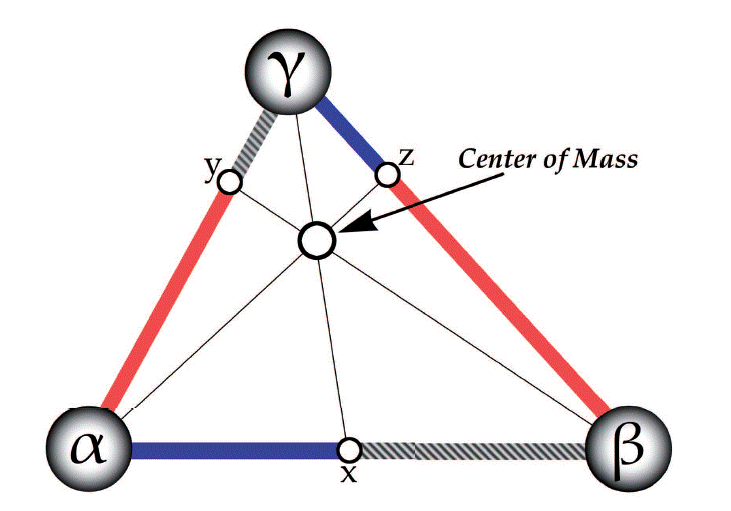
Figure 2: Center of Mass for three particles. x, y, and z are the centers of mass of the particles at the endpoints of the line they sit on.
Can this generalize to deal with four or more particles? What about the case of a collinear trio? It’s easy to extend this procedure to accommodate the non-coplanar four particle case. Namely, the center of mass of four (non-coplanar) particles, α, β, γ, and δ, is the point, c, inside the tetrahedron they form such that a straight line through each vertex/particle (e.g., α) and c will intersect the tetrahedron’s opposing face (△βγδ) at the center of mass of the remaining three vertices/particles (β, γ, and δ). When it comes to the cases of three or more collinear, four or more coplanar particles (etc.), things get a bit trickier. The simplest move we could make would be to chain these procedures together, e.g., finding the center of mass of the first two particles, call it ‘c 1’, and then taking the “center of mass” of the third particle and c 1. The problem with this move is that it means we need to talk about c 1 standing in mass ratios, which means we must assign it a mass.
This looks to require an application of (ADD-BRIDGE), or something in that vicinity. So that method is off limits, for now. In a moment, I’ll describe a view that allows us to assign “approximate effective mass” to composite objects and to centers of mass based on their dynamic behavior,10 as determined using only the masses of simple particles and the ratio relations between them. For example, by looking at the successive locations of the center of mass of a system over a period of time we can determine their “motion”, which we can compare to predictions behavior for massive simples. It’s not hard to make this comparison either. Suppose α and β are a 2g and 3g particle, respectively, 5mm apart and at relative rest. If β accelerates to
But what if we wanted to keep our procedure as unadulterated by additivity as possible? There are a few options. Returning to the 3 particle collinear example, one thing we could do is treat this as a limiting case of the non-collinear case, and use a sequence of non-collinear centers of mass to narrow down its position.12 So we can determine centers of mass by appealing to the ratio structure of mass along with the ratio structure of length. As far as I can tell, this account avoids all of the problems McQueen had with Feather’s account, with one exception: I (like Feather) do not deduce that the position of the composite is the same as the position of its center of mass. I am not even remotely sympathetic to McQueen’s worry here. The position of the composite isn’t at any single point in space. However, we sometimes use the change in position of the center of mass of an object as a way to quantify certain kinds of motion (especially for objects which are spatially spread out). That’s all that’s necessary for my purposes here.
2 . 4 . Rigid Composite Bodies
One might take issue with our progress thus far. Centers of mass are not literal bodies. They’re idealized constructs, useful for simplifying the calculations involved with making predictions about a system, but not what really explains that system’s dynamical behavior. Even if (ADD-BRIDGE) isn’t necessary to determine centers of mass, it may well be that mass additivity play a crucial role in the actual physics behind how composite bodies behave.
Let’s put this worry to rest.13 Consider a body, call it “MOLECULE”, composed of the 2g particle, α, and the 3g particle, β. Suppose α and β are “bound together”, either via some electromagnetic forces or by small, powerful, massless string, in such a way that MOLECULE counts as a rigid body (so the distance between α and β does not change, even when they are impressed by forces).
Given the masses of α and β, the dynamical laws, will predict that, under ordinary conditions, MOLECULE will behave roughly like a 5g simple.
Neither mass additivity nor appeal to center of mass is necessary to determine MOLECULE’s motion. In Newtonian Mechanics, rigid bodies (like MOLECULE) obey what’s called the “Transmissibility Principle”, which says that “[t]he effect of an external force on a rigid body remains unchanged if that force is moved along its line of action”.14 That is, if we apply a force of 2N (two Newtons) to α, in the direction of β, this will have the same effect on the molecule’s motion as if a force of the same magnitude in the same direction were applied to β, as illustrated in Figure 3.
This is true both of total net force, and for component forces. So the same physical effect on MOLECULE’s motion could be achieved by applying a force of 1N both to α and to β, in the same direction (also illustrated in Figure 3). Likewise for .5N and 1.5N, or 1.99N and .01N, or, indeed, any pair of force strengths, F α and F β (such that F α + F β = 2N), applied to α and β in this way.15
Suppose we apply a force of 2N to α as depicted at the top of Figure 3. What will MOLECULE’s acceleration be? Since MOLECULE is a perfectly rigid body, the distance between α and β must remain the same at all times. This means that the force applied to MOLECULE in the direction depicted must induce, in α and β, the same rate of acceleration in that direction (since, if it induced different accelerations in α and β, the distance between them would change).
This constraint, together with F = ma provide us with three equations and three unknowns:
(5) tells us that the component forces on α and β must sum to 2N, while (6) and (7) tell us that the acceleration induced by those forces must be the same (viz.
The result16 is that, both particles accelerate at a rate of
What about if MOLECULE isn’t a perfectly rigid body? Then we would need a specification of the precise forces (or what have you) holding α and β together to determine (1) if application of a 2N force on one of the two particles is strong enough to break MOLECULE apart,19 (2) if it doesn’t break apart, how it deforms, and (3) given how it deforms, how long it takes to return to equilibrium. This adds complexity for sure, but no part of the story will require any mass facts over and above α and β’s respective masses and the mass ratio between them.
This same kind of reasoning can be followed in other cases (e.g., gravitational attraction) to show that the dynamics of the molecule composed of α and β and the predicted dynamics for a 5g point particle will (in most cases) closely mirror one another. Insofar as ascribing a mass to an object amounts to describing how the laws predict it will move around (and influence others’ motions) then we can see how the physical significance of ascribing a mass of 5g to MOLECULE can be captured in the dynamics of Newtonian Particle Mechanics by the masses of, and mass ratios between, simples alone.
2 . 5 . Summary
We’ve seen that the body composed of α and β bound together will, typically, behave like a 5g massive simple. I’ve argued that no part of this dynamic story -and, more generally, no part of mass’s role in the dynamical laws of Newtonian Particle Mechanics -appeals to mass additivity, or a principle like (ADD-BRIDGE).
On its own, this result is fairly innocuous. Few accounts of mass depend on mass additivity, or the intrinsic mass properties of composites, playing an ineliminable role in explaining mass dynamics. One could use this result to support a view that eschews a fundamental principle of additivity like (ADD-BRIDGE) in favor of a derivative principle of “approximate additivity”. This would be a principle that ascribes only “effective masses” to composites based on their dispositions to behave. Such a view definitely has its advantages.20 However, it’s more than a little awkward to have to posit a deep metaphysical distinction between how simple particles have mass (viz. fundamentally and intrinsically) and how all other intuitively “massive” objects do (viz. only approximately, in virtue of the dynamical law-governed behavior of its simple parts).
While the arguments in this section certainly open things up for such an account, the mere viability of such a view is not, in and of itself, an argument that we need to accept a non-fundamental account of mass additivity. In the next section, however, I’ll argue that there are strong explanatory considerations against views that posit mass additivity not grounded in/dependent on its dynamics. In the section after that, we will extend the worry to fundamental summation structure.
3 . An Explanatory Worry about Additivity
In this section, I argue that not only do we not need to posit mass additivity in addition to the dynamics of massive simples, but we shouldn’t do so, if our theory is to be explanatorily adequate. The idea is this: To accept (ADD-BRIDGE) as a fundamental principle (or, at least, as fundamental as the quantity itself) is to adopt a metaphysics of the physical world containing both (1) the instances of the (ADD-BRIDGE) law (composites being assigned mass properties), and (2) the approximation of additivity we get from the Newtonian dynamical laws and the masses of simples. These two patterns exhibit striking correlations21 (as we’ve seen in section 2) even though they are metaphysically independent and wholly distinct phenomena.
Here’s why that’s a problem: MOLECULE is composed of the 2g particle, α, and the 3g particle, β, so (ADD-BRIDGE) entails that (and explains why) this body instantiates the mass property we call “5g”. But (from section 2), the masses of and mass ratios between simple particles entail that (and explain why) MOLECULE behaves roughly like how the laws predict a 5g simple particle would. But (and this is the kicker) these two explanations have almost no overlap, which means the obvious correlation between them -that they both associate MOLECULE with the same mass magnitude, viz. 5g- cannot be explained. Let me put this more precisely:
3 . 1 . The Explanatory Argument against Independent Additivity
In Newtonian Particle Mechanics, the following correlation holds between a composite object’s mass property and its dynamic behavior:
(E1) ∀x(x is a composite body with massive parts→ (x behaves roughly like a fundamental particle of mass M ↔ x instantiates M))
From section 2, additivity is not necessary to capture dynamics. So the dynamical explanation for the behavior of massive composites would be the same regardless of whether or not we posit (ADD-BRIDGE):
(ADD-BRIDGE) If x and y are massive, don’t overlap, and compose z, then (i) z is massive, and (ii) z’s mass is the sum of x’s mass and y’s mass.
If (ADD-BRIDGE) is accepted as a primitive posit (or as otherwise independent of mass’s dynamics) then (by construction) the explanation for why a composite object instantiates a particular mass property won’t depend on its dynamics. The explanation for why a composite has the mass it does would be the same even if the dynamical laws were completely different (or if there were no dynamical laws at all).
So the explanations for a composite object instantiating a mass property and for that object’s dynamic behavior, are independent. These explanations, that is, have no overlap that could explain (E1). Recall MOLECULE.
(F1) The mereological sum of α and β behaves similarly to a 5g simple.
(F2) The mereological sum of α and β has a mass of 5g.
If additivity is independent of dynamics, than the explanation of (F1) is wholly independent of the explanation of (F2). (F2) is just shy of a brute fact, as it’s grounded directly in (ADD-BRIDGE), a fundamental metaphysical posit. (F1), on the other hand, depends on mass’s ratio structure, its role in the dynamics, the nature of forces, and how the laws treat massive simples that are bound together.
Mass additivity, via (ADD-BRIDGE), plays no role in the explanation of the behavior of MOLECULE. This means that it’s a coincidence that massive composites behave, under these dynamics, so similarly to same-massed simples. That is, while it’s not a coincidence that MOLECULE has the mass that it does, nor is it a coincidence that it behaves the way it does, it is a coincidence that these two descriptions always pick out the very same mass property. So a view with independent additivity cannot explain why the striking correlation, (E1), obtains. Taking mass additivity to be fundamental, or otherwise independent of mass dynamics, commits us to widespread unexplained choreography.22
3 . 2 . The Completeness of Dynamical Explanations
I’ve argued that we shouldn’t posit a notion of mass additivity that’s independent of mass dynamics. One might try to get around it by suggesting that (ADD-BRIDGE), when it holds, offers some additional explanation of the behavior of composite bodies. That is, it makes some explanatory contribution over and above the explanation due to the dynamical laws.
This is implausible. There’s nothing about the behavior of composite objects that seems unexplained on a view that captures the dynamics but rejects (ADD-BRIDGE). Indeed, it’s plausible that the dynamic explanation for the motion of an object composed of massive particles is complete in a very strong sense. That is, the explanatory contribution made by the determinate masses of,23 and ratio relations between, simple particles “exhausts” the explanatory contribution of mass, or anything about mass, to the dynamics of material bodies in Newtonian Particle Mechanics. If the dynamic explanation is a complete explanation in this way, then there is no room for (ADD-BRIDGE) to explain anything else about the dynamic behavior of composite bodies. This point will be important in the next section, where I extend the explanatory worry to show that similar problems arise even for certain views without a primitive additivity bridge law.
4 . Dynamics and Quantitative Structure
I’ve already noted an obvious way a theory of mass can avoid the argument in section 3: Do away with fundamental mass additivity principles like (ADD-BRIDGE). We know from section 2 that nothing in our theory of dynamics changes if we drop it. All that we lose is the ascription of fundamental mass properties to composites.24
In this section I argue that the same considerations which tell against independent additivity also apply to views which take summation structure as fundamental (or otherwise independent of dynamics).
Such views include many popular accounts of mass, or of quantity in general. These include accounts in the Hölderian tradition, including those defended by Mundy (1987) as well as Eddon (2013b). Mundy and Eddon both posit determinate mass magnitudes as distinct universal properties, and introduce second-order universals that relate those first-order mass properties, including a fundamental mass ordering relation and a fundamental three-place relation, ‘[∗]’ or ‘Mass-Sum’, between determinate mass properties -we say “5g is the ‘Mass-Sum’ of 2g and 3g”- distributed according to primitive axioms. This objection will also apply to predecessors of these views, going back at least to Hölder (1901), whose “Die Axiome der Quantität und die Lehre vom Mass”25 presents an account of the formal structure of quantities themselves, based on a series of axioms that introduce an ordering and summation relation over determinate magnitudes (which behaved in largely the same way as the first-order universals of the view’s modern descendants). Peacocke (2015 and 2019) is another proponent of fundamental summation structure (and, perhaps, even fundamental additivity) in his account of extensive quantities. “the [ . . . ] notion of addition of magnitudes has application” it’s not clear if by “addition of the magnitudes” he means mass summation structure alone, or mass summation across the mass magnitudes together with the mereological phenomenon that we would capture with something like (ADD-BRIDGE).
There are other accounts that might also face this objection. Something like fundamental summation structure is assumed in the “mass space” account proposed in Arntzenius and Dorr 2012, Chapter 8, “Calculus as Geometry”, on at least one interpretation. Summation structure (understood in terms of concatenation) is foundational in any view one gets out of a “metaphysical” reading of Krantz et al. (1971). Ted Sider treats summation structure as part of a natural and explanatory theory of mass, in his 2012 and 2016. Likewise, Wolff (2020) has recently developed an account called “substantival structuralism”, which combines a commitment to something like a Hölderian metaphysically fundamental quantitative structuring relations (including summation, which Wolff calls “concatenation”), with a sophisticated substantivalism about the relata of those relations.26
So why think my objections against additivity extend to mass summation structure in general? There’s a queer sort of tension, if not quite an inconsistency, in admitting that there’s an explanatory failure inherent in fundamental additivity laws, while claiming no such failure is faced by fundamental mass summation -i.e., facts about which mass properties are “sums” of others, like when we say “5g is the sum of 2g and 3g”. (ADD-BRIDGE) directly appeals to mass’s summation structure. To reject a fundamental/independent additivity principle is to deny that mass’s summation structure has any direct mereological consequences. However, even without (ADD-BRIDGE), the mass summation relation alone is enough to pick out a unique mass-value as the “sum” of the mass-values of a composite’s massive parts. My earlier objection against fundamental additivity is that there’s a striking, unexplained correlation between a composite’s dynamical behavior and the mass magnitude that composite instantiates.
To maintain that this argument is sound, but that primitive summation facts are unproblematic, is to claim that, in the case of MOLECULE, the correlation between (F1) and (F2), above, demands explanation only because MOLECULE itself instantiates the mass 5g. But that a composite instantiates the sum of the masses of its parts is just the surface symptom of a much deeper explanatory failing. To reject (ADD-BRIDGE) but keep fundamental summation structure means that you accept a principle like (F3),
(F3) The Mass-Sum of α’s mass and β’s mass is the mass magnitude 5g
but deny that (F3) implies (F2), since there’s nothing to bridge that gap. However, the correspondence between (F1) and (F3) doesn’t seem to be any less striking, or any less in need of explanation. Removing the symptom merely made the underlying problem a bit more cumbersome to describe. We could, then, bring the problem right back by replacing “x instantiates mass M” in (E1) with something like “x is composed of massive parts, y and z, whose mass properties bear Mass-Sum to M”. Or, more perspicuously:27
(E2) ∀x∀y∀z(x is composed of non-overlapping massive parts, y and z) → (x behaves roughly like a simple particle of mass M ↔ M is the Mass-Sum of y and z’s masses))
4 . 1 . The Big Difference
However, there is a very important asymmetry between the previous argument against fundamental mass additivity and this argument against fundamental mass summation structure. Recall the argument from 2.1, which established that mass additivity is not necessary (at least in Newtonian Particle Mechanics) for our dynamic explanations to go through. Once we have the dynamical laws, all we need regarding mass are the masses of simple particles and the mass ratios between them. We cannot run such an argument in the case of mass’s summation structure. Indeed, mass summation, on many views, does play a key role in explaining mass dynamics.
For example, according to Mundy (1987) , mass summation and mass ordering relations, Mass-Sum and ≤ Mass , are second-order relations distributed over the universal mass properties according to fundamental primitive axioms. Mass ratio relations -the relations we denote with predicates of the form “n-times as massive as” (n ∈ R)- are grounded in facts about the distribution of the summation and ordering relations between mass properties (via representation and uniqueness theorems). Something analogous will hold for any other view in the Hölderian tradition. Likewise, Peacocke (2019) takes mass summation to be fundamental -or at least as fundamental as the quantity itself- and, in his seven principles of the meta-physics of magnitudes, he makes use of summation structure (specifically adding a magnitude with itself) to generate the ratio structure over the magnitudes in a broadly Eudoxan28 manner (Principle IV), and then uses that ratio structure in explaining how magnitudes can feature in causal-explanatory laws (Principle VII). Mass summation, therefore, partially explains mass ratio and, in turn, mass dynamics!
You might wonder, then, how we could get an explanatory worry off the ground in light of this asymmetry. How could it be, that is, that the dynamic behavior is not explained by mass’s summation structure when it’s grounded in that structure (at least partially)? Certainly unexplained choreography is bad, but when the choreography is between something derivative and its grounds, then it isn’t unexplained!
This objection misses the key point of the argument. The problem with mass’s summation structure is not that it doesn’t in any way explain the dynamics, in the sense of metaphysically explain. If this was my argument, I would already be sunk, since it clearly does; summation grounds mass ratios, which in turn ground mass’s role in the dynamics. But that’s not my argument, this is:
4 . 2 . The Explanatory Worry Revived
Fundamental summation structure is unable to explain the correspondence, illustrated by (E2), between the distribution of the Mass-Sum relation -determined by a primitive axiom- and the dynamic behavior exhibited by composites of massive particles. Even though mass’s summation structure can explain the dynamics, it does nothing to explain (E2). The reason for this is because the only way that summation structure explains the dynamics is via its role in grounding mass’s ratio structure. The mass ratios, in turn, determine mass’s role in the dynamics, and the way mass ratio structure determines the dynamics is insensitive to whether and how those mass ratios are grounded. In particular, it’s insensitive to whether they’re grounded in something with the formal character of the Mass-Sum relation! This is why mass’s summation structure fails to explain the systematic correspondence between the “sum” of the mass properties of the parts of an object and the dynamic behavior of that object, despite the fact that the former happens to play some role in grounding the latter.
Put another way, my claim is this: Recall that the explanatory contribution made by the mass ratios between simple particles (together with their intrinsic masses) exhausts the explanatory contribution of mass, or anything about mass, to the dynamics of material bodies in Newtonian Particle Mechanics. While it’s true that facts about the mass summation relation do explain some aspects of dynamics, they do so only insofar as they ground mass ratios. Nothing distinctive about mass summation can be explanatory. There is nothing that Mass-Sum contributes to the explanation of the dynamics that would distinguish it from some alternate basis that might instead ground mass ratios.
And there are a variety of such alternatives. Some have been defended elsewhere in the literature, like the comparativist (i.e., where, fundamentally, there are no mass properties, only comparative mass relations) account, due to Bigelow et al. (1988) , which only admits of mass ratio relations (and ratio relations between those ratio relations).29 Other alternatives would include views which resemble Mundy or Eddon’s except, instead of a second-order Mass-Sum relation, posit some other primitive relation between mass properties to ground mass ratios. Some of these primitives might be less likely to be treated as a serious competitors -like one where a three place “Mass-Avg” relation maps pairs of mass magnitudes to the magnitude that’s their average-, but the mere possibility and intelligibility of such alternative bases is enough to show that nothing about what Mass-Sum contributes to explaining mass dynamics could be distinctive of the Mass-Sum relation (since the alternative relations would also explain via the mass ratios).30
Why does “distinctiveness” matter? Because the mere fact that the dynamics of composites of massive particles is partially dependent on mass’s summation structure does not automatically explain their correspondence. For this dependence to explain (E2), it must be able to “see”/distinguish the specific features of the Mass-Sum relation which exhibit the correspondence with the dynamics. But, as I argued in the last paragraph, that’s simply not the case. If the way that mass ratios explain dynamics is insensitive to, for instance, whether they’re grounded by facts about a fundamental Mass-Sum relation rather than a fundamental Mass-Avg (or something else entirely), then the explanatory connection (entirely mediated by the mass ratios) between the dynamics and Mass-Sum is not able to explain their choreography.
4 . 2 . 1 . An Analogy: Absolute Space and Explanation
It might be helpful to consider an analogy from debates about the metaphysics of space and time. The “Dynamic Leibniz Shift” is an influential objection to Newton’s substantivalist account of absolute space and time. For Newton, all motion of material bodies was motion relative to the background of absolute space (a persisting, concrete physical thing which can, but needn’t be, occupied by matter at any given time). On this view, there could be many distinct, physically possible worlds which agree about what physical bodies there are, the relative velocities between those bodies at every point in time, but which disagree about their absolute velocities. For instance, in one world, the center of mass of the universe is at absolute rest while, in the other world, all the relative motions are the same but the center of mass of the universe is in absolute motion 200km/h in the direction from here to Philadelphia.
Newtonian mechanics with absolute space takes these worlds to be genuinely physically distinct (one’s moving, the other isn’t!). However, it’s a theorem of Newtonian mechanics that we can only ever detect the relative velocities between objects, and the absolute accelerations (changes in velocity over time) of objects. So the Newtonian substantivalist, in accepting absolute velocities, is committed to in-principle undetectable physical structure. This, in the eyes of Leibniz and his ilk, is a cardinal sin.
It’s sometimes claimed31 that this argument doesn’t just show that absolute velocity is in-principle unobservable, it also shows that it’s physically unexplanatory. That is, on a Newtonian physical theory, only the relative velocities between objects, and the absolute accelerations (changes in velocity over time) of objects make a difference to the dynamic behavior of the world. No explanation of dynamic behavior, it’s claimed, will turn on what the absolute velocities (unless you include facts about absolute velocities under ‘dynamic behavior’).
However, this is not quite true. After all, relative velocities and absolute accelerations are physically explanatory, and, on Newton’s view, objects’ absolute velocities through absolute space ground their relative velocities. But this doesn’t mean that there’s no explanatory defect in absolute velocities. Rather, what’s indicated is that the explanatory contribution of relative velocities and absolute accelerations saturate or exhaust the explanatory contribution of Newtonian absolute space to the dynamics. Their explanations are insensitive to whether they are grounded in x being at absolute rest and y moving at absolute velocity v, or y at rest and x moving at −v. So, while the Newtonian substantivalist can say that absolute velocity does explain the physics on their view, they still must concede that nothing about those dynamical explanations depends on anything distinctive about the underlying absolute velocities. And so, the Newtonian must admit that the very same explanatory contribution (of relative velocities and accelerations to the dynamics) can be had in, e.g., a Galilean or “Neo-Newtonian” spacetime32 in which there are no absolute velocities, but there are, still, relative velocities and accelerations (though they have different grounds).
The problem with positing fundamental sub-metrical quantitative structure, like ordering and summation, for mass is due to a similar kind of insensitivity of the physically explanatory thing (in this case, mass ratios) to the nuances of its grounds. Just as nothing about how the relative velocities explain depends on anything distinctive about the actual absolute velocities, nothing about how the mass ratios explain the dynamics depend on anything distinctive about the fundamental Mass-Sum relation, or about which particular trios of mass magnitudes it relates.
4 . 3 . Would My Argument Work without Point Particles?
The arguments presented in the last few sections rely on a very particular physical setup. We restricted our attention to worlds governed by Newtonian laws of nature and populated with massive point particles. This is not an unusual setup by any measure. If anything it’s a strikingly normal case, one you might expect a metaphysician of physics to use as her toy physics to motivate an argument which she claims will apply anywhere. “Weirdness” is not the problem. The problem, rather, is that some of these steps of the argument don’t seem possible at all if we abandon the restriction to worlds populated by massive point particles.
Consider an alternate setup. The laws are those of Newtonian Mechanics with gravitation, but the massive bodies are no longer mere point particles. Rather, they are spatially extended composites that can always be divided into smaller and smaller massive bodies.33 At this world, a critic might say, there is no privileged set of fundamental particles over which to distribute the mass magnitudes. In order for us to assign a mass magnitude to each of these massive bodies in a consistent way, we need to appeal to mass’s summation structure. Without it, there would be nothing to stop a whole from being less massive than its parts! So additivity and summation structure are needed to capture the dynamics after all!
There are two responses we can make to this worry. The first is that we should be suspicious of any theory which has significant theoretical problems when applied to a non-aberrant real world physical theory. Newtonian mechanics with point particles is anything but aberrant, so a theory of mass which is forced to posit widespread unexplained choreography at such worlds is, ceteris paribus, a bad theory. Indeed, one of the key motivations that led Mundy to second-order absolutism in the first place was that first-order comparativist accounts of quantity34 could only get off the ground given certain worryingly contingent assumptions about the physical world. These views could only adequately determine mass’s ratio structure at sufficiently well populated and variegated worlds.35 As such, for second-order absolutist fans of additivity and/or independent summation structure to brush the arguments in this paper aside because they’re restricted to certain specific physical pictures amounts to giving up one of the key advantages of a second-order theory of quantity: Its necessity.
The second response is that it’s at all not obvious that summation structure really is needed to capture the dynamics of infinitely divisible massive solids. The argument that we need summation structure to explain the dynamics is based on the observation that, at continuously divisible worlds, the mereological relations between the various massive bodies constrain which distributions of mass magnitudes over those bodies are physically possible. The idea is that we could produce the needed constraints by demanding that our distribution of mass magnitudes be in keeping with (ADD-BRIDGE). And it’s certainly true that we could do it that way. However, this is not the only way to generate such constraints. We can obtain the same result by appealing to mass’s ratio structure and the dynamical laws, requiring that the distribution of mass magnitudes give rise to a consistent dynamics. This will prevent a massive object’s parts from being more massive than the whole; a force applied to a massive body must produce the same change in motion regardless of whether we consider it to be a single massive body, or a composite of numerous smaller massive bodies, etc.36 I won’t argue for this in any detail here, but there’s good reason to expect that, at least for Newtonian dynamics, a constraint of this sort will be enough to fix the distribution of mass magnitudes to the required extent.
5 . Conclusion
One could try to turn the results of the previous section into an argument against the views of Hölder, Mundy, Eddon, Peacocke, and the others, in favor of some other choice of fundamental quantitative structure, like a ratio-based mass comparativism in the style of Bigelow and Pargetter, or the Mass-Avg view I described, above. At some point, however, we need to ask what we’re doing here. The fact that we can “swap out” substantively different fundamental bases and leave the view’s physical explanatory structure -i.e., explanations the view offers at the level of physics- completely un-changed is evidence that something has gone very wrong with our theorizing about the metaphysics of mass. Given what we know about the distinctive explanatory contribution of these different candidate grounds for mass ratios (or, more accurately, the lack thereof), what worthy justification could we possibly appeal to in championing one over another?
Here’s a reasonable norm: If nothing about the role of mass in our physical theory turns on P, then (ceteris paribus) P shouldn’t be something that’s central to our fundamental metaphysics of mass. If we take this principle seriously, then Hölderian views, Peacocke-style magnitude realism, even Bigelow and Pargetter’s ratio-based comparativism, as well as any more Hölderian-like comparativism,37 and many others all proceed from the exact wrong starting point.
This, moreso than any particular unexplained correlation, I take to be the strongest consideration against such accounts.38
The fan of independent summation structure might try to defend their view a different way, by appealing to some notion of “naturalness” or “familiarity” in their choice of primitives. But this would be a truly bizarre position to take up, given the what I argue here. Summation structure -i.e., facts about which masses are “sums” of which others- is only a natural-seeming posit because it looks like behavior we observe in the physical world! Specifically, this structure resembles the concatenation behavior that massive objects exhibit. Indeed, we don’t often use the “sum” locution when describing the mass summation relation between objects; rather, if x instantiates a mass property which is the “sum” of the mass properties of y and z, we say “x is as massive as y and z put together”. Facts about the behavior of composite objects is at the core of our thinking regarding this structure. But my arguments single out precisely this feature of mass summation structure as giving rise to widespread unexplained coincidences!
5 . 1 . Towards a Positive Theory of Mass
In section 2.5, I mentioned a possible view that could avoid these worries by making (approximate) mass additivity dependent on dynamics. The result of the previous section’s argument against independent mass summation structure suggests the similar sort of fix. The moral, on such a view, is that we should take mass additivity and (some or all of) mass’s quantitative structure to be grounded in the dynamics of massive bodies. We should take these results to indicate that the structure of mass, ultimately, encodes something dynamical. Trying to add structure independent of/over-and-above mass dynamics only ends up producing unexplanatory “echoes” of that dynamics at the fundamental level.
While they are not common, relative to other accounts in the metaphysics of quantity, there are some authors who have defended a dynamic theory of mass -i.e., a theory on which facts about mass’s dynamic connection to other quantities grounds both mass additivity and mass’s quantitative structure. This is not a new view, Ernst Mach (1893) proposes a definition of mass which purports to reduce mass to its dynamical role. He describes the view as the claim that ‘inertial mass’ is a “theoretical term” which we define as an object’s capacity to determine the acceleration of other objects, but this is somewhat misleading. Mach does not, in fact, give an account of mass properties, which would be capacities to determine accelerations in other bodies. Rather, he defines mass relations, like “same mass as” or “n-times as massive as”, as theoretical terms concerning the relative capacity of a pair of massive entities to induce accelerations in each other. Other contemporary dynamic theories of mass have been proposed, following Mach. John Burgess (1984) and (1991) develops an account which grounds mass ratios in spatiotemporal ones by equating them with certain distance ratios via what amounts to a primitive “same ratio as” relation massive objects and space-time points,39 and Marco Dees (2018) sketches another kind of nomic reduction of mass according to which “the only physically significant comparisons among physical magnitudes concern the role those magnitudes play in the laws” (p. 821).
An account which grounds mass ratios in mass dynamics turns the common explanatory order on its head. It takes the close correlation between mass ratios and the acceleration ratios of bodies in similar physical conditions as indicative of just what it is to stand in a particular mass ratio. Such a view would elegantly explain the correspondence between quantitative structure and dynamics, as well as adequately capture the physical upshot of mass additivity. The idea is that, if mass properties or mass ratios are defined in terms of dynamics, then having similar dynamic behavior to a massive thing will be a way of (nearly) literally having the same mass. Or, to put it in terms of ratios, if the mass ratios: “n times as massive as” are defined dynamically, then, since the dynamic relation α bears to a 5g simple (based on the differences in, e.g., how they accelerate under the same force) is very similar to the dynamic relation α bears to MOLECULE, then α thereby bears something very similar to the “2/5 th ’s the mass of” relation to MOLECULE. A dynamic theory of mass’s quantitative structure can easily and quite straightforwardly justify the ascription of mass to composite objects, without the need for an additional principle. It integrates the account of mass with the physical significance of mass ratios and mass additivity in an intuitive way.40
Aside: Do All Additive Quantities Depend on Dynamics?
Could we run these same sorts of arguments for additivity quantities other than mass? Though my argument was restricted to mass, many of the accounts I criticize are meant to apply to all scalar quantities (or, in the case of Peacocke, all extensive/additive quantities). One might wonder whether and how far we could generalize these considerations, and worry that they might generalize too far.
I think it would be too quick to conclude from this paper that any quantity which we think has summation structure is such that if that summation structure were part of the ground for its metrical structure then there would be unexplained choreography. Specifically, the precise role that mass plays in the dynamics is an integral part of the arguments in this paper, and they may not extend to quantities who traffic with the physical world a different way. For instance, Perry (2015) has argued that quantities like length and volume have a closer relationship to the mereology of their instances than quantities like mass and charge do. This relationship, which she calls “Proper Extensiveness”, includes both additivity and “subtractivity” (though she doesn’t describe it that way) -where an object necessarily has proper parts of lesser lengths (say) if there are any lesser length properties to be had- is necessary to explain the success of paradigmatic length measurements (e.g., via a ruler), and that this explanation cannot be mediated by length’s dynamics.41 If this argument is correct, then that’s some evidence that length and volume might not be as susceptible to the arguments in this paper.42











 nueva página del texto (beta)
nueva página del texto (beta)




