Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de ciencias pecuarias
versión On-line ISSN 2448-6698versión impresa ISSN 2007-1124
Rev. mex. de cienc. pecuarias vol.15 no.1 Mérida ene./mar. 2024 Epub 12-Abr-2024
https://doi.org/10.22319/rmcp.v15i1.6457
Articles
Generation of new equations to estimate aerial biomass based on morphological variables obtained from grasses in rangelands of Nuevo León, Mexico
aUniversidad Autónoma de Nuevo León. Facultad de Ciencias Forestales. Kilómetro 145, Carretera nacional 85, Linares, N.L. México.
bUniversidad Autónoma de Nuevo León. Facultad de Agronomía. México.
The estimation of aerial biomass of grasses contributes to carrying out efficient and sustainable management of rangelands. This study aimed to generate new equations to estimate the aerial biomass of grasses present in rangelands in Nuevo León, Mexico, based on data collected from the total number (n= 745) of individuals of the five species of grasses: Cenchrus ciliaris Linnaeus, Pappophorum bicolor Fourn, Aristida purpurea Nutt, Tridens texanus Watson and Paspalum pubiflorum Fourn present in the sampling plots. Using the maximum height and the height of the vegetative stems, the aerial, basal, and compressed diameters, and volumes measured in each of the collected individuals, linear (stepwise) and nonlinear equations were generated to estimate the aerial biomass (dry matter basis) of the grasses cut at ground level. Six general equations with the best statistical fit for the total species collected were selected. General equation III had the best values of R2 =0.88 and AIC =3079, using the five variables evaluated. General equation IV had an R2 =0.86 and AIC =3530, using only the variable compressed diameter. The selected specific equations estimated the aerial biomass of the grasses Cenchrus ciliaris (R2=0.88, r=0.94), Pappophorum bicolor (R2 =0.86, r =0.92), Aristida purpurea (R2=0.92, r=0.96), Tridens texanus (R2 =0.91, r =0.96), and Paspalum pubiflorum (R2 =0.93, r = 0.97). The new equations are a reliable alternative to indirectly estimate the aerial biomass of the grasses of the rangelands of northeastern Mexico in a faster and less expensive manner than the traditional method.
Keywords Allometric equations; Cenchrus ciliaris; Native grasses; Compressed diameter
La estimación de biomasa aérea de pastos contribuye a realizar un manejo eficiente y sostenible de los agostaderos. El objetivo del presente estudio fue generar nuevas ecuaciones para estimar la biomasa aérea de pastos presentes en agostaderos, en Nuevo León, México, basado en datos colectados del total (n=745) de los individuos de las cinco especies de pastos: Cenchrus ciliaris Linnaeus, Pappophorum bicolor Fourn, Aristida purpurea Nutt, Tridens texanus Watson y Paspalum pubiflorum Fourn presentes en las parcelas de muestreo. Utilizando la altura máxima y la de los tallos vegetativos, los diámetros aéreo, basal y comprimido, y volúmenes medidos en cada uno de los individuos colectados, se generaron ecuaciones lineales (stepwise) y no lineales, para estimar la biomasa aérea (base materia seca) de los pastos cortados a ras de suelo. Se seleccionaron seis ecuaciones generales con el mejor ajuste estadístico para el total de las especies colectadas. La ecuación general III tuvo los mejores valores de R2=0.88 y AIC=3079, utilizando las cinco variables evaluadas. La ecuación general IV estimó con R2=0.86 y AIC= 3530, utilizando solo la variable de diámetro comprimido. Las ecuaciones específicas seleccionadas estimaron la biomasa aérea de los pastos Cenchrus ciliaris (R2=0.88, r=0.94), Pappophorum bicolor (R2=0.86, r=0.92), Aristida purpurea (R2=0.92, r=0.96), Tridens texanus (R2=0.91, r=0.96), y Paspalum pubiflorum (R2=0.93, r=0.97). Las nuevas ecuaciones son una alternativa confiable para estimar indirectamente la biomasa aérea de los pastos de los agostaderos del noreste de México, de forma más rápida y menos costosa que el método tradicional.
Palabras clave Ecuaciones alométricas; Cenchrus ciliaris; Pastos nativos; Diámetro comprimido
Introduction
The rangelands distributed around the world cover more than 50 % of the earth’s surface and provide biomass that supplies a fundamental ecosystem service on which wildlife, population, and livestock farming, the main economic activity in this ecosystem, depend1,2. In the last century, rangelands have suffered degradation due to episodes of drought and overgrazing due to an excessive stocking rate3,4, due to failures in efficient and sustainable use of the rangeland to cover the forage biomass requirements of the cattle herd5. Therefore, it is essential to have reliable estimates of the amount of forage available for cattle that allow the proper use of forage, avoidance of overgrazing, and the satisfaction of the needs of animals6,7.
The traditional method for estimating aerial biomass production is that of cutting and weighing grass; although this destructive method is accurate, it is usually expensive and time-consuming8,9. In addition, the random distribution of vegetation makes it necessary to increase the recommended number of samples per site (15-20 samples10), ideally collected at each forage growing season8.
Indirect methods (non-destructive, since they do not require cutting the grass present) arise as an alternative to the traditional one (destructive, which involves cutting and weighing the grass present) to determine the aerial biomass of forage in the rangeland since they have the advantage of achieving estimates of the biomass of large areas in a faster way11,12. Subjective empirical methods of visual estimation have the disadvantage of a high variation in results among people who perform them in different periods of time13. Graduated plates or sticks have been used in recent decades to estimate forage biomass in meadows with homogeneous vegetation14,15. New methodologies for biomass estimation have been developed through the use of satellite images16, radar images17, and unmanned vehicles18; however, these are mainly carried out in cultivated areas.
The rangelands have different types of vegetation with heterogeneous distribution. For example, in the Tamaulipan thornscrub (TTS), shrub and semi-shrub species predominate, sometimes constituting more than 80 % of the botanical composition, while grass species and other weeds hardly exceed 10 and 6 %, respectively19,20. Under these conditions, allometric models developed by relating the biomass production data obtained from the traditional method with the measurements made in morphological characteristics of the individual are a good option to estimate the biomass of grasses objectively. Once the model is generated, biomass estimation can only be done by measuring the necessary vegetative variables, without the need to cut the plants5,9.
Studies prior to this work have been conducted in meadows under irrigated and monoculture conditions15,21,22. For rangeland conditions, results obtained under arid conditions in Arizona23 and multispecies conditions in Argentina9 have been published. There are reports of equations generated specifically for estimating the biomass of certain grass species, such as those reported based on 40 plants from C. ciliaris grass meadows in southern Arizona, relating biomass with basal diameter and plant height24, as well as equations generated for A. purpurea in a previous study25, using the diameter of the plant at different heights as variables.
In Europe, an indirect estimation methodology was developed for grass species21, which used a measure called minimum volume, obtained by joining all the stems of the plant by applying a subjective, non-standardized force to form a minimum volume.
The present study aimed to generate new equations to estimate the aerial biomass of five species of grasses present in the rangelands of Nuevo León, Mexico, based on the measurement of their morphological variables, which could serve as an alternative to replace the need to cut grass as in the traditional method.
Material and methods
The study was conducted in an area of 132 ha of rangelands in the municipality of Marín, Nuevo León (25°52'28"N; 100°03'24"W), in which precipitation varies between 400 and 600 mm per year, and the average temperature ranges from 20 to 22 °C26. The primary vegetation type is Tamaulipan thornscrub (TTS), in addition to having areas of induced grassland and agriculture.
In January 2021, 31 sampling plots of 100 square meters (10 m x 10 m) were randomly established within the study area with vegetation typical of the Tamaulipan thornscrub, and five 1 m2 subplots were delimited within each plot, in which was collected and weighed (dry matter basis) all the individuals of grasses present in each of the 155 subplots evaluated, in a design similar to that previously used in areas of rangeland27. A perimeter fence was placed around each plot to prevent disturbances. All plots were cut at 3 to 5 cm height at the beginning of the study and in each sampling. The first sampling was conducted from June 15 to July 15, 2021, and the second was conducted in the autumn from October 18 to November 8, 2021. In both cases, the sampling was carried out 30 to 40 d after a rainfall greater than 150 mm (in the first sampling) and 231 mm (in the case of the second sampling) since, according to previous studies28, the flowering of the Cenchrus ciliaris grass occurs between 25 and 35 d after regrowth as a result of precipitation of 150 mm, which is considered as the threshold for the productivity of the species Cenchrus ciliaris29 during the summer and autumn.
In each subplot, all plants of the grass species present were sampled and identified individually at the genus and species level. A Truper® pro-Lock FX-5M tape measure was used to measure the variables described below and shown in Figure 1A:
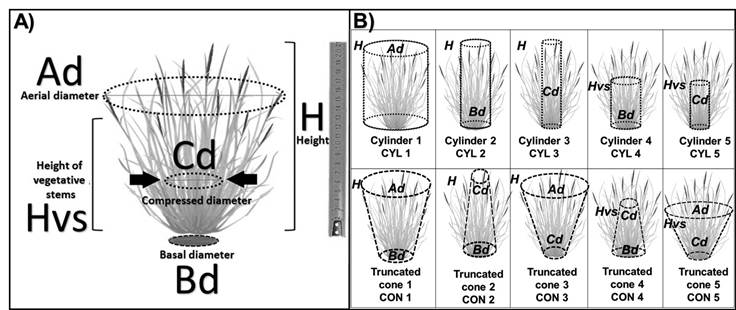
H= height ; Hvs= height of vegetative stems ; Bd= basal diameter; Cd= compressed diameter; Ad= aerial diameter.
Figure 1 Variables measured in grass plants (A) and shapes of estimated volumes (B)
Maximum height (H): distance between the ground and the highest part of the stems and leaves.
Height of the vegetative stem (Hvs): distance between the ground and most vegetative leaves, usually those without a spike.
3Basal diameter (Bd): of the circumference of the base of the plant.
4Aerial diameter (Ad): at the height of the vegetative stems.
5Using Traceable® model 6˝ digital calipers, the compressed diameter (Cd, Figure 1) was measured at half the height of the grass using an experimental prototype that, through a retractable band, applies a graduated uniform pressure of 2 kg on the vegetative stems.
Using the morphological variables of Figure 1A, circular aerial cover (CACOV), ellipsoidal aerial cover (EACOV), circular basal cover (CBCOV), and ellipsoidal basal cover (EBCOV) were calculated. The volumes of the cylinder (in its CYL1 to CYL5 modalities) and cone (in CON1 to CON5 modalities), indicated in Figure 1B, were based on previous proposals30.
Each of the 745 plants sampled was identified, measured, and cut with hand scissors at ground level to record its fresh weight (g) in the field and stored in a Kraft paper bag. Subsequently, the samples were taken to the laboratory and dried in a forced air oven at 60 °C until reaching a constant weight in order to obtain their dry weight (g) by using a scale with a capacity of 500 g with a minimum division of 0.1 g (Torrey brand, model Lab-500).
The 745 individuals found in the sampling subplots were identified, measured, and cut. The plants of the five grass species present in the study area: Cenchrus ciliaris (n= 424 individuals), Pappophorum bicolor (n= 125 individuals), Aristida purpurea (n= 107 individuals), Tridens texanus (n= 59 individuals) and Paspalum pubiflorum (n= 30 individuals) were collected for the generation of equations.
A total of 19 independent variables (aerial diameter, basal diameter, compressed diameter, height, vegetative stem height, circular basal cover, elliptical basal cover, circular aerial cover, elliptical aerial cover, volume of cylinder 1, volume of cylinder 2, volume of cylinder 3, volume of cylinder 4, volume of cylinder 5, volume of cone 1, volume of cone 2, volume of cone 3, volume of cone 4, volume of cone 5) and a dependent variable (measured biomass [g DM] per individual of the grass species) were subjected to linear regression, stepwise regression9 and nonlinear regression (logarithmic, inverse, quadratic, cubic, power, exponential) analysis in the IBM SPSS software to generate biomass prediction equations both generally and specifically (for each of the five grass species found in the samplings).
To assess the quality of the biomass estimate achieved with the new general and specific equations, each of the values recorded in the destructive sampling was compared with the predicted values of each of the equations. The coefficient of determination of the regression (R2)27, the standard error (SE)30, Pearson’s correlation (r)18, the normalized root mean squared error (NRMSE)21, and the Akaike information criterion (AIC)27 were calculated.
The six general equations developed with the best statistical fits of AIC, NRMSE, R2, SE, and r were selected to estimate the total species collected, and a specific equation was selected for each of the five recorded grass species.
Results
The grasses Cenchrus ciliaris and Paspalum pubiflorum presented values of aerial and basal cover, aerial and basal diameter, and fresh and dry weight (P<0.05) higher than the rest of the species (Table 1). Cenchrus ciliaris recorded an average value of dry weight per individual higher than that of Aristida purpurea and Tridens texanus (P<0.05), while Paspalum pubiflorum and Pappophorum bicolor obtained intermediate values.
Table 1 Average values of aerial cover, basal cover, aerial diameter, basal diameter, compressed diameter, maximum height, height of vegetative stems, fresh weight, and dry weight per individual of each species in 1 m2 experimental subplots
| Species. | Cover | Diameter | Height | Weight | |||||
|---|---|---|---|---|---|---|---|---|---|
| AER (cm2) |
Basal (cm2) |
AER (cm) |
Basal (cm) |
Compressed (mm) |
MAX (cm) |
Vegetative stems (cm) |
Fresh (g) |
Dry (g) |
|
| Cenchrus ciliaris | 729ab | 190a | 28a | 14a | 19a | 52a | 27a | 53a | 22a |
| Pappophorum bicolor | 355bc | 52bc | 20bc | 8bc | 13abc | 52a | 23ab | 15bcd | 10ab |
| Aristida purpurea | 277bc | 29c | 17cd | 6c | 9bcd | 45ab | 20bc | 7cd | 5b |
| Tridens texanus | 208c | 37bc | 16cd | 6c | 6d | 34cd | 16c | 5d | 3b |
| Paspalum pubiflorum | 799a | 104abc | 30a | 11ab | 13ab | 40bc | 23ab | 48ab | 13ab |
AER= aerial; MAX= maximum.
abcd Different letters within the same column indicate a significant difference (P<0.05).
The estimates of aerial biomass calculated with the six new general equations generated in the present study had coefficients of determination (R2) that varied between 0.77 and 0.90, while Pearson’s correlation coefficient (r) ranged from 0.88 to 0.94. The normalized root mean squared error (NRMSE) ranged from 0.68 to 0.48, and the Akaike information criterion (AIC) took values from 3553 to 3079 (Table 2).
Table 2 General and specific allometric equations generated based on morphological variables to indirectly estimate the aerial biomass of grasses (g DM-1)
| Id | Equation | R2 | SE | r | NRM SE |
AIC |
|---|---|---|---|---|---|---|
| General equations | ||||||
| I | Y= 0.9648 + 0.0026CON5 | 0.77 | 10.1 | 0.88 | 0.64 | 3469 |
| II | Y= 2.5343 + 0.0027CON5 + 0.0139CYL3 - 0.0295CACOV +0.8253Cd - 0.2595Hvs + 0.0002CYL1 | 0.87 | 7.8 | 0.93 | 0.49 | 3108 |
| III | Y= 1.2159 + 0.0032CON5 + 0.0447CYL3 - 0.0421CACOV + 0.8939Cd - 0.3478Hvs + 0.0003CYL1 - 0.0253CON2 + 0.5790Bd + 0.0084CYL2 | 0.88 | 7.5 | 0.94 | 0.48 | 3079 |
| IV | Y= 0.1213 * Cd 1.6818 | 0.86 | 0.4 | 0.88 | 0.67 | 3530 |
| V | Y= 0.4473 * CYL3 0.7288 | 0.89 | 0.4 | 0.88 | 0.68 | 3553 |
| VI | Y= 0.8084 * CYL5 0.7078 | 0.90 | 0.4 | 0.88 | 0.67 | 3530 |
| Specific equations | ||||||
| C.c. | Y= 0.2862 + 0.0032CON5 - 0.0753CACOV + 1.4623Cd - 0.0767CON4 + 0.0279CYL4+ 0.0902CBCOV - 0.3257Hvs + 0.0022CYL1- 0.0032CON1 + 0.0931CYL5 | 0.88 | 9.0 | 0.94 | 0.40 | 1603 |
| P.b. | Y= 2.1060 + 0.0490CYL3 + 0.0050CON4 + 0.0002CON3 - 0.0050EBCOV | 0.86 | 3.0 | 0.92 | 0.29 | 287 |
| A.p. | Y= -0.6641 + 0.1138CYL5 + 0.1257Ad + 0.0046CON2 - 0.0816CBCOV + 0.1951Cd | 0.92 | 1.5 | 0.96 | 0.27 | 87 |
| T.t. | Y= 0.5474 + (0.1672 * CYL3) + (-0.0012 * CYL3) + (1.18 × 10 -5 * CYL3) | 0.91 | 0.9 | 0.96 | 0.30 | -18 |
| P.p. | Y= -0.0371 +(0.2744 * CYL3) + (-0.0020 * CYL3) + (6 × 10-6 * CYL3) | 0.93 | 2.3 | 0.97 | 0.24 | 57 |
Linear model equations= I, II, III, C.c., P.b., and A.p.; Power model equations= IV, V and VI; Cubic model equations= T.t. and P.p.; Y= Aerial biomass (g DM-1); R2= Coefficient of determination; SE=Standard error; r= Pearson’s correlation coefficient; NRMSE= Normalized root mean squared error; AIC= Akaike Information Criteria; C.c.= Cenchrus ciliaris; P.b.= Pappophorum bicolor; A.p.= Aristida purpurea; T.t.= Tridens texanus; P.p.= Paspalum pubiflorum. See Figure 1 for Bd, Ad, Cd, H, Hvs, EBCOV, CBCOV, CACOV, CYL1, CYL2, CYL3, CYL4, CYL5, CON1, CON2, CON3, CON4, CON5. All regression coefficients were significant (P<0.05).
The variable cylinder 3, calculated from the height of the plant and the compressed diameter, was the basis for generating the specific equations for Tridens texanus and Paspalum pubiflorum in the cubic model, whose estimates had a fit of R2 of 0.91, r=0.96, NRMSE=0.30, AIC=-18 for Tridens texanus (Figure 2F) and R2=0.93, r=0.97, NRMSE=0.24, AIC=57 for P. pubiflorum.
Equation I is a linear model that incorporates the measurement of cone 5 (Figure 1B), which is calculated based on three direct variables (aerial diameter, compressed diameter, and height of the vegetative stems), and whose estimates have an R2 of 0.77, r=0.88, NRMSE=0.64, AIC=3469. The estimates calculated with equation II (linear) from the data generated by the variables aerial diameter, compressed diameter, height, and height of the vegetative stems have an R2 of 0.87, r= 0.93, NRMSE= 0.49, and AIC= 3108. Equation III (linear) incorporates the data of the five measured variables to calculate estimates that have an R2 of 0.88, r= 0.94, NRMSE= 0.48, AIC= 3079 (Figure 2A).
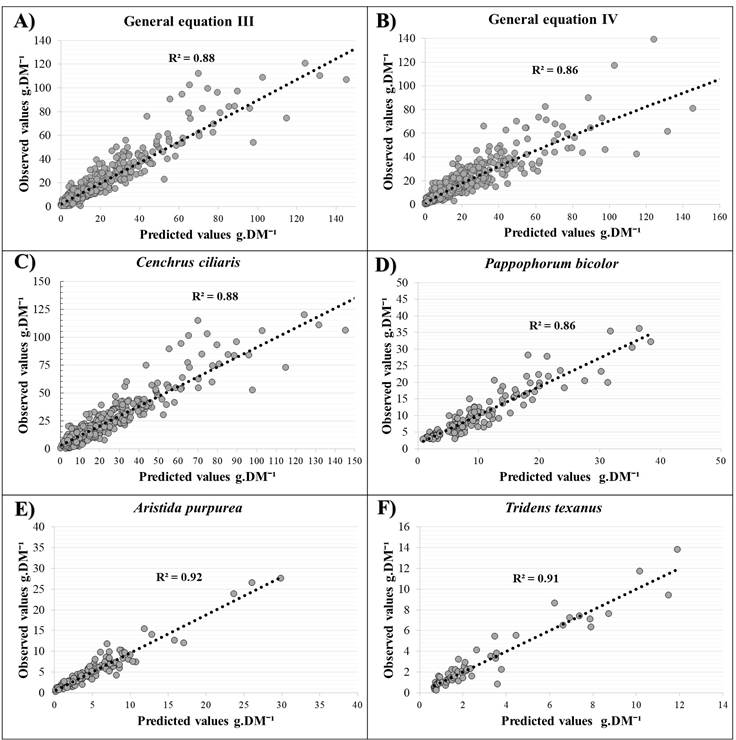
A) General equation III (Table 2). B) General equation IV (compressed diameter). C) Specific equation for Cenchrus ciliaris. D) Specific equation for Pappophorum bicolor (Table 2). E) Specific equation of Aristida purpurea. F) Specific equation of Tridens texanus (Table 2). All graphs were set to zero.
Figure 2 Regression of predicted values and observed values
Nonlinear equations IV (R2= 0.86, r= 0.88, NRMSE= 0.67, AIC= 3530; Figure 2B), V (R2= 0.89, r= 0.88, NRMSE= 0.68, AIC= 3553) and VI (0.90, r= 0.88, NRMSE= 0.67, AIC= 3530) are from the power model and use fewer variables. The estimates calculated using equation IV, which uses the compressed diameter as the only variable, have an R2=0.86 (Figure 2B). Equation V uses cylinder 3, calculated from the compressed diameter and height of the plant, to estimate aerial grass biomass with R2=0.89. Equation VI uses cylinder 5 (Figure 1B), calculated from the compressed diameter and height of the vegetative stems, to estimate aerial biomass with R2= 0.90 (Table 2).
In the case of equations generated specifically for each of the grass species, comparisons between the estimated values and the results recorded directly from aerial biomass yielded R2 values from 0.86 to 0.93. The values of r (Pearson) ranged from 0.92 to 0.97. For NRMSE, values from 0.40 to 0.24 were recorded, and AIC took values from 1603 to -18 (Table 2). In the specific case of the equation generated for Cenchrus ciliaris, a good fit of the estimated values of aerial biomass was achieved, with R2 of 0.88, r= 0.94, NRMSE= 0.40, AIC= 1603, using the five variables measured (Figure 2C).
The results estimated using the five variables with the specific equation for the species Pappophorum bicolor (Table 2) had a fit of (R2= 0.86, r =0.92, NRMSE= 0.29, AIC= 287) (Figure 2D).
The information collected from 107 individuals of Aristida purpurea allowed the generation of a specific equation for this grass species (Table 2), whose estimates, based on the five variables measured, had a fit with a coefficient of determination of 0.92, r=0.96, NRMSE= 0.27, AIC= 87. (Figure 2E).
Discussion
The linear and polynomial equations generated in the present study based on the sampling of vegetative measurements and biomass weight records of grasses present in the rangeland allowed the estimation of the aerial biomass of grasses present in the rangeland with a high degree of precision.
The new general allometric equations established in the present study had values of R2 (0.77 to 0.93) higher than those previously reported (R2 from 0.25 to 0.85) for estimates of general equations for two grasses and two pseudo-grasses in the Peruvian Andes27. Allometric equations generated in Chubut, Argentina23, by evaluating 50 individuals from three species of grasses, had R2 values (between 0.72 and 0.86) similar to those obtained in the present study.
The number of plots established in the present study was similar to that previously used27; however, in the present study, there were plots of 100 m2, while in the previous study27, they had plots of 4 m2. In addition, in each of the 31 plots of the present study, the values of botanical composition, vegetative measurements, and biomass of the grasses present in five subplots were recorded. With this, there was greater reliability of the recorded measurements and the calculated averages for the generation of the equations.
The species C. ciliaris had a significant presence in the grass vegetation observed in the rangeland evaluated since it represented 57 % of the total number (n= 745) of individuals collected and its biomass, calculated considering the number of individuals and the average weight of the individuals of the species shown in Table 1, represented 80 % of the biomass recorded in the rangeland evaluated. In the areas assessed in the present study, the C. ciliaris grass present was established by natural dispersion, evidencing its high potential to establish itself in the rangelands in Mexico31. The native species with the highest presence in the present study was Pappophorum bicolor, which had a record of 125 individuals, that is, 17 % of the total, whose biomass represented only 11 % of the total biomass (Table 1).
The compressed diameter was the variable included in 100 % of the general allometric equations and in 97 % of the specific equations, both for the linear and nonlinear model, generated in the present study for each grass species. The height of the vegetative stems was included in 87 % of the general equations. The variables vegetative stem height and plant height were included in 71 % of the specific equations. These variables have been directly related to forage density32. Some authors30 reported that, in meadows with optimal conditions for their development, the variable vegetation cover is the one that can best indirectly estimate the biomass. Mahood et al22 determined that vegetation cover is a good predictor for biomass estimation, with an R2 of up to 0.89 in Bromus tectorum plant communities.
An indirect estimation methodology implemented for grass species in Western Europe21 used a measure called minimum volume as a variable, consisting of manually joining all the stems of the plant until forming a minimum volume; nevertheless, the applied force was subjective, varying according to the person performing the measurement and it could even vary when the same person exerts different pressure due to fatigue when repeatedly making the sampling. By applying the same compression force, the compaction device used in the present work generated greater certainty of the results obtained.
The NRMSE values calculated in each of the new equations generated in the present study determine the dispersion of the estimated data with respect to the observed data, with 0 being the ideal fit33. In contrast, the Akaike criterion compares and selects from a group of prediction models that use the same experimental data the most appropriate to forecast the expected values compared to the observed values, which in this case should be the model with the lowest AIC value34,35. The values of NRMSE and AIC are very useful in the selection of the best models.
The specific equation generated in the present study for Cenchrus ciliaris had a value of R2=0.87, and with it, an R2 similar to that reported in a study (R2 of 0.8224) to generate allometric equations relating biomass with the measurement of basal diameter and height of 40 plants of C. ciliaris grass meadows in southern Arizona. The equation generated in the present study for A. purpurea resulted in an R2= 0.89, similar to those reported (R2 from 0.82 to 0.90) in a previous study25, for the species A. purpurea, using the diameter of the plant at different heights. Some authors30 generated equations to estimate aerial biomass from the analysis of 93 plants of Agropyron desertorum and reported coefficients of variation (R2 from 0.76 to 0.88) slightly lower than those of the present study. The new equations generated in this study are potential candidates to replace the cutting, drying, and weighing phases performed in the traditional method36.
The development of allometric equations with application in rangelands is of utmost importance to achieve sustainable ecosystem management27. These non-destructive vegetation samplings have advantages in terms of time and budget compared to traditional sampling and also allow growth monitoring at the individual level21,37.
Conclusions and implications
The importance of 19 variables related to the morphological characteristics of grasses present in the rangeland was evaluated to estimate the production of aerial biomass per plant. This information was used to generate 6 new general equations for five grass species present in the study area and 5 new specific equations (one for each grass species Cenchrus ciliaris, Pappophorum bicolor, Aristida purpurea, Tridens texanus, and Paspalum pubiflorum), which reliably and practically estimate the production of biomass without destroying (cutting) the plant. The new equations generated in this study are a viable option to replace the cutting phase of the samples in the traditional method of estimating the production of aerial biomass of grasses in the rangeland. The development of general (multispecies) and specific (for a particular grass species) allometric equations is a reliable alternative to indirectly estimate the aerial biomass of the grasses of the rangelands of northeastern Mexico more quickly and less expensively than the traditional method.
Acknowledgments
CONAHCYT is thanked for the scholarship granted to the first author during the development of this research.
REFERENCES
1. ILRI. (International Livestock Research Institute), IUCN. (International Union for Conservation of Nature), FAO. (Food and Agriculture Organization of the United Nations), WWF. (World Wide Fund for Nature), UNEP. (United Nations Environment Programme) & ILC. (International Land Coalition). Rangelands Atlas. Nairobi Kenya: ILRI. 2021 2021 https://hdl.handle.net/10568/114064 . Accessed Apr 1, 2023. [ Links ]
2. Jones MO, Robinson NP, Naugle DE, Maestas JD, Reeves MC, et al. Annual and 16-day rangeland production estimates for the western United States. Rangeland Ecol Management 2021;(77):112-117. [ Links ]
3. Mganga KZ, Musimba NKR, Nyariki DM, Nyangito MM, Mwang'ombe AW. The choice of grass species to combat desertification in semi‐arid Kenyan rangelands is greatly influenced by their forage value for livestock. Grass Forage Sci 2015;70(1):161-167. [ Links ]
4. Williams DG, Baruc Z. African grass invasion in the Americas: ecosystem consequences and the role of ecophysiology. Biolog Invasions 2000;(2):123-140. [ Links ]
5. Murphy DJ, Shine P, Brien BO, Donovan MO, Murphy MD. Utilising grassland management and climate data for more accurate prediction of herbage mass using the rising plate meter. Precision Agric 2021;(22):1189-1216. [ Links ]
6. Mundava C, Helmholz P, Schut T, Corner R, McAtee B, Lamb D. Evaluation of vegetation indices for rangeland biomass estimation in the Kimberley area of Western Australia. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences. 2014;(II-7):47-53. [ Links ]
7. Grüner E, Astor T, Wachendorf M. Biomass prediction of heterogeneous temperate grasslands using an SfM approach based on UAV imaging. Agronomy 2019;9(2):54. [ Links ]
8. Murphy DJ, Murphy MD, O’Brien B, O’Donovan MA. Review of precision technologies for optimising pasture measurement on irish grassland. Agriculture 2021;(11):600. https://doi.org/10.3390/agriculture11070600. [ Links ]
9. Nafus AM, McClaran MP, Archer SR, Throop HL. Multispecies allometric models predict grass biomass in semidesert rangeland. Rangeland Ecol Management 2009;62(1):68-72. [ Links ]
10. Fernández HH. Estimación de la disponibilidad de pasto. Cuadernillo clásico de forrajeras INTA, SAGPYA, Argentina. 2004;(98):9-12. [ Links ]
11. Tackenberg O. A new method for non-destructive measurement of biomass, growth rates, vertical biomass distribution and dry matter content based on digital image analysis. Ann Botany 2007;99(4):777-783. [ Links ]
12. Butterfield HS, Malmström CM. The effects of phenology on indirect measures of aboveground biomass in annual grasses. Int J Remote Sensing 2009;30(12):3133-3146. [ Links ]
13. Andariese SW, Covington WW. Biomass estimation for four common grass species in northern Arizona ponderosa pine. Rangeland Ecology Management/J Range Management Archives 1986;39(5):472-473. [ Links ]
14. Harmoney KR, Moore KJ, George JR, Brummer EC, Russell JR. Determination of pasture biomass using four indirect methods. Agronomy J 1997;89(4):665-672. [ Links ]
15. Damiran D, DelCurto T, Darambazar E, Clark AA, Kennedy PL, Taylor R. Visual obstruction: weight technique for estimating production on northwestern bunchgrass prairie rangelands. In: Proc Western Sec, Am Soc Anim Sci 2007;(58):225-228. [ Links ]
16. Chen Y, Guerschman J, Shendryk Y, Henry D, Harrison MT. Estimating pasture biomass using sentinel-2 imagery and machine learning. Remote Sens 2021;(13):603. [ Links ]
17. Xu K, Su Y, Liu J, Hu T, Jin S, et al. Estimation of degraded grassland aboveground biomass using machine learning methods from terrestrial laser scanning data. Ecological Indicators 2020;(108):105747. [ Links ]
18. Viljanen N, Honkavaara E, Näsi R, Hakala T, Niemeläinen O, Kaivosoja J. A novel machine learning method for estimating biomass of grass swards using a photogrammetric canopy height model, images and vegetation indices captured by a drone. Agriculture 2018;(8):70. [ Links ]
19. Marroquín-Castillo JJ, Alanís-Rodríguez E, Jiménez-Peréz J, Aguirre-Calderón O, Mata-Balderas JM, Chavez-Costa AC. Composición florística y diversidad de un área restaurada post-minería en el matorral espinoso tamaulipeco. Polibotánica 2016;42(1):1-17. [ Links ]
20. Valdez C, Guzmán MA, Valdés A, Forougbakhch R, Alvarado MA, Rocha A. Estructura y diversidad de la vegetación en un matorral espinoso prístino de Tamaulipas, México. Rev Biología Trop 2018;66(4):1674-1682. [ Links ]
21. Pottier J, Jabot F. Non-destructive biomass estimation of herbaceous plant individuals: a transferable method between contrasted environments. Ecological Indicators 2017;(72):769-776. [ Links ]
22. Mahood AL, Fleishman E, Balch JK, Fogarty F, Horning N, Leu M, et al. Cover-based allometric estimate of aboveground biomass of a non-native, invasive annual grass (Bromus tectorum L.) in the Great Basin, USA. J Arid Environ 2021;(193):104582. [ Links ]
23. Flombaum P, Sala OE. A non-destructive and rapid method to estimate biomass and aboveground net primary production in arid environments. J Arid Environ 2007;69(2):352-358. [ Links ]
24. McDonald CJ, McPherson GR. Creating hotter fires in the Sonoran Desert: Buffelgrass produces copious fuels and high fire temperatures. Fire Ecology 2013;39(4):26-39. [ Links ]
25. Sorensen GE, Wester DB, Rideout-Hanzak S. A nondestructive method to estimate standing crop of purple threeawn and blue grama. Rangeland Ecol Management 2012;65(5):538-542. [ Links ]
26. INEGI. Instituto Nacional de Estadística y Geografía. Prontuario de información geográfica municipal de los Estados Unidos Mexicanos Marín, Nuevo León. Clave geoestadística 19034. México, 2009. [ Links ]
27. Oliveras I, Eynden M, Malhi Y, Cahuana N, Menor C, Zamora F, et al. Grass allometry and estimation of above‐ground biomass in tropical alpine tussock grasslands. Austral Ecol 2014;39(4):408-415. [ Links ]
28. González Y, Mendoza F. Determinación del momento óptimo de cosecha de las semillas de Cenchrus ciliaris híbrido CIH-2. Pastos Forrajes 1996;19(1):59-64. [ Links ]
29. Martin MH, Cox JR, Ibarra FF. Climatic effects on buffelgrass productivity in the Sonoran Desert. Rangeland Ecol Management/J Range Management Archives 1995;48(1): 60-63. [ Links ]
30. Johnson PS, Johnson CL, West NE. Estimation of phytomass for ungrazed crested wheatgrass plants using allometric equations. Rangeland Ecol Management/J Range Management Archives 1988;41(5):421-425. [ Links ]
31. Siller-Clavel P, Badano EI, Villarreal-Guerrero F, Prieto-Amparán JA, Pinedo-Álvarez A, et al. Distribution patterns of invasive buffelgrass (Cenchrus ciliaris) in Mexico estimated with climate niche models under the current and future climate. Plants 2022;11(9):1160. [ Links ]
32. Barnetson J, Phinn S, Scarth P. Estimating plant pasture biomass and quality from UAV imaging across Queensland’s Rangelands. Agri Engineering 2020;2(4):523-543. [ Links ]
33. Soto-Bravo F, González-Lutz MI. Análisis de métodos estadísticos para evaluar el desempeño de modelos de simulación en cultivos hortícolas. Agronomía Mesoamericana 2019;30(2):517-534. [ Links ]
34. Martınez DR, Albín JL, Cabaleiro JC, Pena TF, Rivera FF, Blanco V. El criterio de información n de Akaike en la obtención n de Modelos Estadísticos de Rendimiento. Conference: XX Jornadas de Paralelismo. Coruña, España. 2009;439-444. [ Links ]
35. Cavanaugh JE, Neath AA. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Wiley Interdisciplinary Reviews: Computational Statistics 2019;11(3):e1460. [ Links ]
36. INIFAP (Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias). Ajuste de carga animal en tierras de pastoreo, Manual de capacitación. Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias Cuajimalpa. México. 2011. [ Links ]
37. Mills A, Smith M, Moot D. Relationships between dry matter yield and height of rotationally grazed dryland lucerne. N Z Grasslands 2016;(78):185-196. [ Links ]
Received: May 04, 2023; Accepted: September 25, 2023











 texto en
texto en 


