Introduction
Groundwater plays a substantial role in resource supply, in ecosystem functioning and human well-being. Worldwide, 2.5 billion people depend solely on groundwater resources to satisfy their basic daily water needs, and hundreds of millions of farmers rely on groundwater to sustain their livelihoods and contribute to the food security of so many others (UNESCO, 2012). Groundwater is an important source of water supply due to its relatively low susceptibility to pollution in comparison with surface water and its large storage capacity (US EPA, 1985. Therefore it has to be protected from the increasing threat of subsurface contamination due to the rising of environmental problems. Identification of highly susceptible areas is a first and necessary step toward preventing groundwater pollution. This will allow a given region to be classified into sub-regions in terms of their vulnerability intensity and relevant measures to be designed that will prevent pollution from reaching vulnerable areas (Mohammadi, Niknam, & Majd, 2009; Umar, Ahmed, & Alam, 2009).
The term aquifer pollution vulnerability is used to represent the intrinsic characteristics which determine the sensitivity of an aquifer to being adversely affected by an imposed contaminant load. Aquifer vulnerability is primarily and logically a function of the inaccessibility of the saturated zone, in a hydraulic sense to the penetration of pollutants and of the attenuation capacity of the strata overlying the saturated zone as a result of physical retention, and chemical reaction with contaminants (Foster, 1987). There are several approaches for developing aquifer vulnerability assessment maps such as DRASTIC (Aller, Bennett, Lehr, & Petty, 1987), GOD (Foster, 1987), AVI (Van Stempvoort, Ewert, & Wassenaar, 1993), and SINTACS (Civita, 1994). A comprehensive detail of these methods is given in Vrba and Zaporozec (1994) and in Gogu and Dassargues (2000).
The result of these methods is a map which shows different categories of aquifer vulnerability, with qualitative classes typically ranging from very low to very high vulnerability. Frequently, these methods presents limitations or difficulties, for example the use of a qualitative definition of groundwater vulnerability, as opposed to a definition based on a quantitative way (Gogu, Hallet, & Dassargues, 2003;Frind, Molson, & Rudolph,2006; Popescu, Gardin, Brouyere, & Dassargues, 2008); or homogeneity in the results, which does not allow to discriminate and delimit areas of different vulnerability to pollution. This is of central importance in the development of aquifer protection strategies, but many areas around the world frequently show strong homogeneity in the results of aquifer vulnerability assessment, which represents, to decision makers, a problem that has not been addressed yet (Massone, Quiroz Londoño, & Martínez, 2010).
The fuzzy set theory may be used to assess groundwater vulnerability due to the existence of fuzzy nature of the groundwater vulnerability. This can be explained by the transition from the easiest to be polluted to the most difficult to be polluted. Basic concepts of approximate reasoning with fuzzy logic were first presented by Zadeh (1965). Approximate or fuzzy reasoning (Zadeh, 1975; Zadeh 1976; Zadeh, 1992) significantly extends the ability to reason with imprecise information, which is typically found in natural resource science (Reynolds, Jensen, Andreasen, & Goodman, 2000). Application of fuzzy logic to natural resource science and management is still relatively new, but growing rapidly. General areas of application include watershed management and planning (Reynolds, Jensen, Andreasen, & Goodman, 2000; Guertin, Fiedler, Miller, & Goodrich, 2000; Barreto-Neto & De Souza, 2008; Aher, Adinarayana, & Gorantiwar, 2013), groundwater pollution risk evaluation(Dixon, Scott, Dixon, & Steele, 2002; Dixon, 2005; Uricchio, Giordano, & Lopez, 2004; Chowdary, Rao, & Sarma, 2005; Nobre, Rotunno-Filho, Mansur, Nobre, & Cosenza, 2007), water quality assessment (Scannapieco, Naddeo, Zarra, & Belgiorno, 2012; Gharibi, Mahvi, Nabizadeh, Arabalibeik, Yunesian, & Sowlat, (2012)) 2012, environmental impact assessment (Liu, & Yu, 2009) and evaluating ecosystem sustainability (Prato, 2005).
Compared to classical rule-based systems (Waterman, 1986), knowledge representation for problem specification using fuzzy logic is more precise, compact, and efficient. Research has shown that fuzzy rule-based models are capable of producing comparable results using about 40% fewer variables (Bardossy & Disse, 1993). Generally, groundwater vulnerability assessments routinely deal with incomplete data. One solution to the problem of missing data is to tailor an assessment to existing data. The aim of this study is to develop a tool to assess the groundwater vulnerability through fuzzy predicates in an area at the Pampas Plain (Argentina) using fewer variables than other ordinary methods.
Study area
The study area is located to the southeast of Buenos Aires Province within the subregion Wet Pampa, covering a total area of 1000 km2. Climatic conditions are highly variables, Wet Pampa is characterized by a humid climate, very good soils and a resulting high agricultural productivity (soya beans, wheat, sunflowers, corn, potatoes) which is the main sustenance of the country’s economy.
Dulce Stream is originated in the Tandilia Range System and flows into the Mar Chiquita lagoon (Figure 1). The area of the lagoon was incorporated as a MAB Reserve (Man and Biosphere Program, UNESCO) in 1996 due to the high conservational value of its biodiversity related to different ecological regions (plains, flood plains, marshes, deltas, barrier of dunes) (Iribarne, 2001).
The area reveals extreme flatness, with an elevation ranging from 2 to 357 meters above sea level with ranges of the Tandilia System in the upper basin. The Tandilia Range System in the area consists of two big geological units: a Precambrian crystalline bedrock called Complejo Buenos Aires (Marchese & Di Paola, 1975), and a set of sedimentary rocks of Precambrian-Lower Paleozoic origin, grouped under the name of Balcarce Formation (Dalla-Salda & Iñiguez, 1979). They are both considered as the hydrogeological bedrock. The aquifer is formed by silts and silty-to-sandy sediments with variable amounts of calcium carbonate which can reach a thickness of up to 100 m (Sala, 1975; Massone, Tomas, & Farenga, 2005; Quiroz Londoño, Martínez, Massone, Bocanegra, & Ferrante, 2006). Recharge to the aquifer system mainly predominates in the hilly area and it is due to infiltration of precipitation excess, and discharge occurs towards surface streams and water bodies.
The study area was chosen according to criteria that included the high level of agricultural activities and the available data regarding aquifer geology. From a hydrological point of view this area involves significant local extraction of groundwater resources for drinking water and irrigation.
Methodology
Ordinary method for groundwater pollution vulnerability assessment
DRASTIC method considers the following seven parameters: depth to water (D), net recharge (R), aquifer media (A), soil media (S), topography (T), impact of the vadose zone (I), and hydraulic conductivity (C). Each parameter has been evaluated in reference to the others in order to determine the relative importance of each, and have been assigned a relative weight, ranging from 1 to 5. The most significant parameters are given a weight of 5, whilst the least significant receive a weight of 1.
Each DRASTIC parameter is subsequently classified into ranges (for continuous variables) or into significant media types (for thematic data) which have an impact on pollution potential. The DRASTIC model has a rating range for each parameter. The typical rating range is from 1 to 10. Here, a value of 10 would indicate an area with the highest groundwater vulnerability, whilst a value of 1 would indicate the lowest groundwater vulnerability. The final vulnerability index (Di) is a weighted sum of the seven parameters and can be computed using the formula:
Where Di is the DRASTIC index for a mapping unit, w is the weight factor for each parameter and r is the rating for each parameter. The higher the Di, the greater the groundwater pollution vulnerability. There are two types of DRASTIC systems. One is a general DRASTIC system and the other is a pesticide DRASTIC system. The pesticide DRASTIC system, called DRASTIC-P, is designed to be used where the main concern is the application of pesticides to an area. It differs from the assignment of weights (Table 1). In this study, DRASTIC-P was selected according to the agricultural expansion in the zone. Ranges and ratings for the DRASTIC-P parameters, averaged for the study area on a regional scale, were obtained from previous studies (Massone, Tomas, & Farenga, 2005; Auge, 2004; Lima, Zelaya, & Massone, 2011).Plain and Perirange Fringe were defined with different data values. The hydraulic conductivity parameter on a regional scale was assumed a constant.
Table 1 Weight factors for DRASTIC and DRASTIC-P (Aller, Bennett, Lehr, & Petty, 1987).
| Thematic map | Weight | |
|---|---|---|
| Drastic | Drastic-P | |
| Depth to water table (D) | 5 | 5 |
| Net recharge (R) | 4 | 4 |
| Aquifer media (A) | 3 | 3 |
| Soil media (S) | 2 | 5 |
| Topography(T) | 1 | 3 |
| Impact of vadose zone (I) | 5 | 4 |
| Hydraulic conductivity (C) | 3 | 2 |
The work was carried out with the preparation of base thematic maps (as a polygonal entity) for each parameter using GIS software packages. Subsequently, each map was transformed to raster format (using spatial analysis module). Then, the application of map algebra to obtain the groundwater vulnerability map, called “DRASTIC-P model”, was applied.
Fuzzy logic method for groundwater pollution vulnerability assessment
The use of fuzzy logic predicates is proposed to assess the groundwater pollution vulnerability, as a natural extension of Boolean logic predicates. Knowledge is represented as a main fuzzy predicate whose degree of truth is computed through numerical variables to determine a degree of groundwater pollution vulnerability.
Fuzzy logic predicates definitions
#1. A fuzzy predicate p is a linguistic expression with an associated degree of truth µ(p) into [0, 1] interval. It applies the “principle of gradualism” which states that a predicate may be both true and false, having some degree of truth (or falsehood) assigned.
#2. A simple fuzzy predicate p is a fuzzy predicate whose degree of truth µ(sp) can be obtained by some of the next alternatives: 1)The application of a membership function associated with a fuzzy term, to a quantitative variable; e.g. sp = "intensity is high" is associated with the variable "intensity" which is measured in meters and the concept "high" is defined by a membership function over the magnitude of the intensity. 2) The association of discrete values into the interval (0, 1) to language labels (generally adjectives) of a variable; for example: variable "intensity", and its labels "high": μ(sp) = 0.9; "medium": μ(sp) = 0.5; "low": μ(sp) = 0.1. 3) Determination of a real value into the (0, 1) interval directly by an expert. It is normally required in situations of some subjectivity where there is a variable that cannot be quantified by using one of the two previous cases, e.g. "Infrastructure is adequate".
#3. A compound predicate cp is a fuzzy predicate obtained by combination of simple fuzzy predicate or other compound fuzzy predicates, joined by logical connectives and operators (and, or, not, implication, double-implication). For example: cp = cp1 and (cp2 or sp1) and sp2.
#4. Compound predicates can be represented as a tree structure, having its nodes associated by logical connectives (and, or, not, implication, double-implication) and the successive branches related to lower hierarchical level predicates (simple or compound). The root of the tree corresponds to the main compound predicate and leaves are simple predicates.
Fuzzy logic predicate model
TFS (Thematic Fuzzy System) software has been developed using MATLAB® to design and optimize a Fuzzy logic predicate model to assess the pollution vulnerability of groundwater in a study area. It tackles Fuzzy Logic concepts by means of a friendly graphical user interface.
TFS consists of three main stages:
Stage 1. Selection of variables and source of data
Variable selection was performed based on two aspects: previous hydrogeological knowledge of the study area and available information of soil. There are two variables most directly related to the vulnerability to pollution:
Water table depth (m).
Ease of the unsaturated zone in order to favors the infiltration of contaminants. This is composed of the percentage of organic matter in soil, the percentage of clay in the soil and topographic slope of the terrain.
Data of water table depth were obtained from previous studies (Lima, Zelaya, & Massone, 2011); topographic slope from Digital terrain model and cartography (National Institute of Geography of Argentina (IGN) and Shuttle Radar Terrain Mission (SRTM)). Finally, organic matter in soil and soil texture from National Institute of Agricultural Technology-INTA, map of soils.
Stage 2. Determination of the fuzzy predicate tree and membership functions
For the tree design, a predicate tree structure must be provided. The root is the main predicate to evaluate, and leaves are the simple predicates. Simple predicates are intended to be evaluated by data. Composed predicates are characterized by a logical operator (and, or, not, implication, double implication) and associated to simple predicates that act as arguments for that operator. The degree of truth of the simple predicates can be obtained by membership functions (Triangular, Trapezoidal, Gaussian, Sigmoid).
The next linguistic predicates were evaluated in the proposed model:
“The groundwater x is vulnerable when the aquifer is shallow and the unsaturated zone allows the infiltration of pollutants”.
“The unsaturated zone allows the infiltration of pollutants when it is found that the slope is low, the unsaturated zone does not contain clay neither organic matter”.
Formally:
V(x) = “The groundwater x is vulnerable when the aquifer is shallow or the unsaturated zone allows the infiltration of pollutants.”
where:
S(x) = “The aquifer is shallow.” P(x) = “The unsaturated zone allows the infiltration of pollutants.”
The P(x) predicate can be disaggregated using three simple predicates, as:
where:
L(x) = “The slope is low.” C(x) = “The unsaturated zone does not contain clay.” M(x) = “The unsaturated zone does not contain organic matter.”
The following predicates were considered:
“The aquifer is shallow” S(x). It was considered that if the water table depth is between 0 to 2 meters then the worst condition is presented, because any pollutant discharge into surface rapidly reaches groundwater. Between 2 and 5 meters the negative potentiality decreases rapidly, while between 5 and 15 meters it gradually loses significance since the greater depth allows time for the existence of chemical or biological degradation of the pollutant. Depths greater than 18 meters were considered the less harmful (Aller, Bennett, Lehr, & Petty, 1987).
“The slope is low" L(x). The worst situation occurs when the slope is less than 2% slope. Since this value is gradually increasing, the runoff exceeds the infiltration. Slope values greater than 18% are considered less dangerous situation (Aller, Bennett, Lehr, & Petty, 1987).
“The unsaturated zone does not contain clay" C(x). Values between 0 and 10% are considered as the worst situation; from 10% presence of clay is likely to appear delay phenomena, each of them acting increasingly important to a value of 30% of clay. The presence of more than 30% is considered the less dangerous situation (Gao, Maguhn, Spitzauer, & Kettrup, 1998).
“The unsaturated zone does not contain organic matter” M(x). The worst situation was considered for values less than 2%. From that value to 7% the delay processes manifested being gradually more significant. Values of organic matter of more than 7% are considered the less hazardous (Gao, Maguhn, Spitzauer, & Kettrup, 1998).
Based on the previous stage, a fuzzy predicate tree was developed (Figure 2) and membership functions were defined (Figure 3). Shape selection and parameterization of membership functions is a heuristic and iterative process guided mainly by expert knowledge. The function type chosen were Double Gaussian for the “The aquifer is shallow”, Sigmoid for “The unsaturated zone does not contain clay”, and Trapezoidal for “The unsaturated zone does not contain organic matter” and for “The slope is low”. It allowed a wide range of values to take the maximum value and then to descend gradually. Depending on the function type, a different number of parameters is required and their interpretation changes. Function parameters indicate the decay speed and positions of breaking points for Double Gaussian functions (for the right and left side, Figure 3, a). They determine the slope and the value for 0.5 degree of truth for Sigmoid function (Figure 3, b) and they indicate the four breaking points for Trapezoidal functions (Figure 3, c,d).
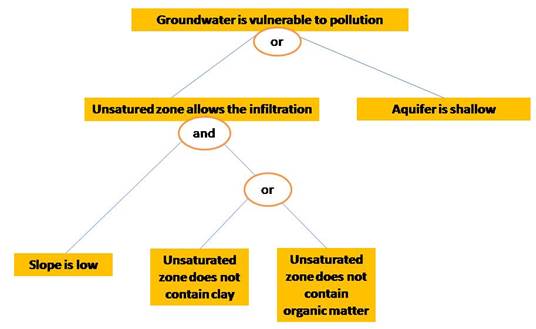
Figure 2 Fuzzy predicate tree for groundwater pollution vulnerability assessment. Leaves of the tree are evaluated by membership functions and upper branches are obtained by operating with the degrees of truth.
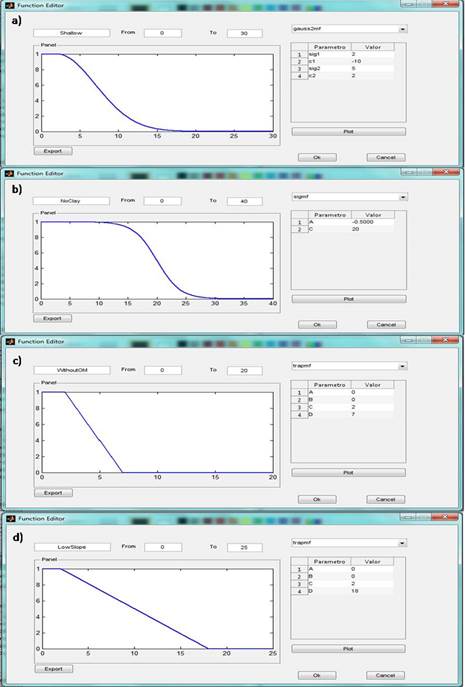
Figure 3 Membership functions for groundwater pollution vulnerability assessment. a) Double Gaussian for the “The aquifer is shallow”, b) Sigmoid for “The unsaturated zone does not contain clay”, c) Trapezoidal for “The unsaturated zone does not contain organic matter” and d)Trapezoidal for “The slope is low”.
Stage 3. Processing and exportation to Geographic Information System
TFS allows specification and numerical evaluation of a fuzzy predicate tree. Input variables are equidimensional matrixes coming from maps in raster format. Output (answer) is a matrix with the same dimensions. The final map (output matrix) shows the degree of truth for the main predicate, for each pixel. This degree of truth (indicating the relative groundwater pollution vulnerability) is represented using a color scale in the map. The software allows exporting as a map file to a Geographic Information System which converts ASCII to raster format. A spatial cell resolution of 100 m ×100 m was used. All GIS information was projected in Argentine Gauss Krüger system, zone 6 (Campo Inchauspe Datum). Table 2 shows the main differences between the methods proposed.
Table 2 Main differences between DRASTIC model and Thematic Fuzzy System.
| DRASTIC model | Thematic Fuzzy System | |
|---|---|---|
| Method | Boolean logic | Fuzzy logic predicate model |
| Parameters | Seven parameters | Four parameters |
| Presentation of results | Discrete, classification in categories. | Continuous data |
| Semantic implication of tags | High: "higher restriction" Moderate: uncertainty Low: "higher level of permission" | Results through tags degree of truth, with less semantic implication. |
| Greater difficulty of the method | Territorialization of the variables | Define predicates and membership function |
| Greater advantage of the method | Methodology widely used and tested internationally | Greater discrimination of the territory in degree of truth of the main predicate |
Results
Groundwater pollution vulnerability assessment by DRASTIC model
The groundwater vulnerability map using the DRASTIC-P model shows a high homogeneity of results: for instance, more than 70 % of the area is classified as having moderate vulnerability (Figure 4 and Table 3). DRASTIC-P map indicate that approximately, all of the highest and lower parts of the Dulce Stream Basin, except a narrow strip in the highest, fall under the high vulnerability classification.
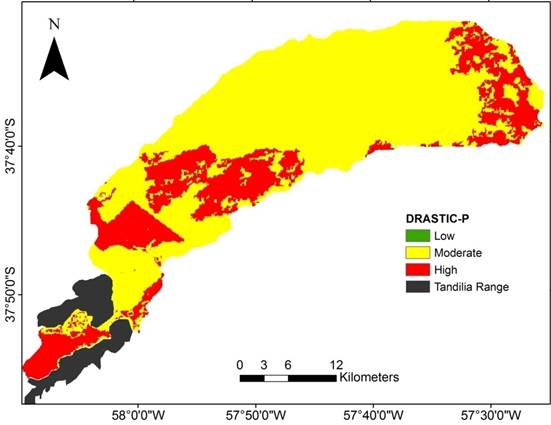
Figure 4 Groundwater vulnerability map according to original DRASTIC-P model in the Dulce Stream Basin.
Table 3 Vulnerability categories and their areas.
| Dulce Stream Basin | ||||
|---|---|---|---|---|
| Methodology | Rank | Category | Area (Sq.km) | % Area |
| DRASTIC-P | < 120 | Low | 6.09 | 0.62 |
| 120-160 | Moderate | 733.9 | 74.52 | |
| 160-180 | High | 244.64 | 24.85 | |
Groundwater pollution vulnerability assessment by TFS model
The fuzzy membership functions provide an explicit mathematical expression for testing an observation's degree of affinity for the concept represented by fuzzy terms. Fuzzy truth values in TFS range from 0 (totally false, or no evidence) to 1 (totally true, or full evidence). Results in terms of truth values for the overarching predicate “groundwater is vulnerable” are described below. Figure 5 shows the partial products of the entire evaluation process; from viewing this composite, it is possible to see the various contributions to overall groundwater pollution vulnerability. A summarize of the results of the partial products are mentioned immediately below:
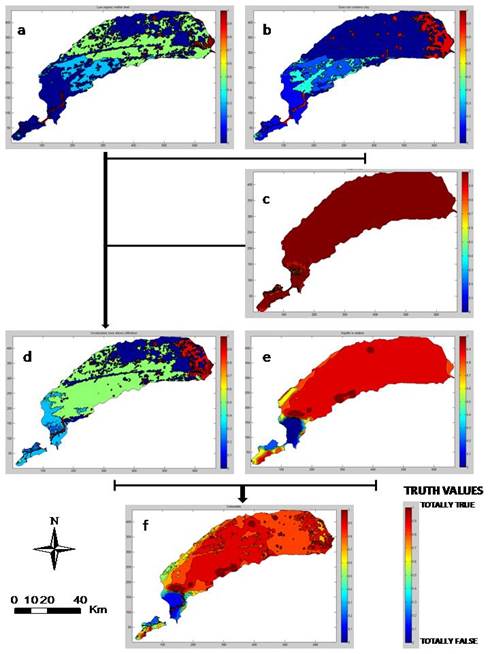
Figure 5 Composite of all partial product evaluations leading to the full assessment of groundwater pollution vulnerability for the Dulce Stream Basin: a) M(x): “The unsaturated zone does not contain organic matter”; b) C(x): “The unsaturated zone does not contain clay”; c) L(x): “The slope is low”; d) P(x): “The unsaturated zone allows the infiltration of pollutants”; e) S(x): “The aquifer is shallow”, and f) V(x): “The groundwater is vulnerable”.
Throughout the middle and lower basin, evaluation of water table depth showed high to very high truth values for predicate S(x), conducting to high groundwater pollution vulnerability. In contrast, results in the upper portion of the study area were low truth values showing a low to very low contribution to groundwater pollution vulnerability from groundwater condition. This is consistent with the geomorphology of the study area, gently sloping plain in the middle and lower basin and hills in the upper basin. Evaluation of water table depth in the upper portion had low to very low contribution to groundwater pollution vulnerability due to a high thickness of the vadose zone (> 20 m).
The unsaturated zone condition is composed of the evaluations of slope, clay and organic matter content. The upper basin showed small truth values for the predicate P(x). On the other hand, the middle basin displayed moderate values of truth in large part of the area, while the lower portion was mixed in truth values showing low and high evidence (Figure 5, d). Considering the secondary topics, the slope in the most part of the area presented low values (< 1º), therefore it displayed conditions that conduct to a low surface run off and favor water infiltration, being the worst condition for groundwater pollution vulnerability. Related to clay, the upper and middle basin presented small truth values for the predicate C(x), while the lower basin showed high truth values. It is due to that appropriate soil media characteristics in the upper basin, mainly clay loam texture, contribute to low groundwater pollution vulnerability. While the lower portion had especially high evidence for contributing to groundwater pollution vulnerability since the sandy loam soil texture dominate this sector. Regarding organic matter content in the unsaturated zone, the upper basin displayed very low truth values for the predicate M(x). However, the middle and lower basin presented low and moderate truth values. The presence of loam to clay loam soil textures in the upper basin and sandy soil texture in the low basin explain these obtained results for the predicates C(x) and M(x).
The final map of the groundwater pollution vulnerability for Dulce Stream Basin (Figure 6) evidenced pronounced differences in groundwater pollution vulnerability between the different portions of the study area. Generally, low truth values for the predicate V(x) was detected in the upper basin. On the contrary, the middle and lower basin presents high to very high truth values for the groundwater vulnerability. This map is the result of the partial products of the entire evaluation process previously described.
Discussion
One of the limitations of the traditional methods for the groundwater vulnerability assessment in plain areas is that it shows a high homogeneity of results. Many plain areas with unconfined aquifers present homogeneity in most of the parameters involving vulnerability assessment (especially in the case of the traditional GODS or DRASTIC methods), mainly at local and regional scales. Therefore traditional assessment methods of groundwater vulnerability present results whose homogeneity makes decision-making altogether difficult. These decisions may be about land use restrictions, monitoring plans, environmental impact assessment, or other aquifer protection strategies. Consequently, the homogeneity of results in the lower categories of vulnerability (even though it makes decision-making easier) may lead to excessive confidence, leading to a rejection of protection measures or decisions taken with scarce attention to prevention (Massone, Quiroz Londoño, & Martínez, 2010). With reference to the vulnerability assessment through DRASTIC method in the Dulce Stream Basin, Figure 4 showed that the category of “moderate vulnerability” implies more than 70% of the area. This label has a high degree of uncertainty, since the meaning of this category is not accurately defined. On the other hand, the final fuzzy map proposed for the Dulce Stream Basin identified the middle and lower basin as areas with high and very high truth values for the main predicate “Groundwater is vulnerable”, thus, these sectors are defined as the main areas of greatest vulnerability of groundwater in the basin. The model obtained from fuzzy logic is more restrictive than the DRASTIC method, since the portions of the area where DRASTIC evidence “moderate vulnerability”, the logic model shows high and very high vulnerability.
The TFS developed to assess the groundwater pollution vulnerability allowed improve the problem of homogeneity of the used hydrogeological variables in plain areas. The fuzzy logic model provides a framework for processing linguistic knowledge and its corresponding data through membership functions for groundwater pollution vulnerability assessment.
Conclusion
Results in the fuzzy logic model showed a continuous transition from low to high truth values for the main predicate “Groundwater is vulnerable”, which is in fact fuzzy nature of groundwater vulnerability to contamination. In this regard, the TFS generates a continuous vulnerability function unlike of the ordinary methods of groundwater pollution vulnerability assessment, in fact it could be a pronounced advantage over the traditional methods. With a comparison between fuzzy model and ordinary DRASTIC models, it was found that generally, in the ordinary DRASTIC model, the areas covered by classes have a more uniform distribution between the categories compared with fuzzy model and in terms of mapping, ordinary DRASTIC has a high homogeneity in the vulnerability map compared with fuzzy model which all of these issues are as a result of the nature of Boolean logic applied in structure of DRASTIC method.
In the implementation of planning and water resource management these spatial models can help describe the aquifer system, provide knowledge-based formulation of possible actions, simulate consequences or actions of decision possibilities, and assist in the formulation of implementation strategies. Spatial decision situations are often complex, multidisciplinary, and usually involve many stakeholders. It is important relevant information concerning the issue must be acquired and organized to support problem analysis. This study showed that fuzzy rule-based models, such as the TFS, are more efficient computer-base tools for decision-makers in the water resources management due to high discrimination of the territory, producing successful results using fewer variables than other classic approaches.











 nueva página del texto (beta)
nueva página del texto (beta)





