Introduction

A lactation curve is the result of an explanation of a biological process with a mathematical function¹, and is useful in predicting total production from partial samples. Milk production is represented by the lactation curve trajectory, and is influenced by genetic and environmental factors². Lactation curves help to understand milk production physiological behavior and can be used to research the genetic potential of a dairy cattle herd or breed³. By applying lactation curves, total milk production can be predicted with one or a number of measurements taken on control days in early lactations⁴. Milk production genetic potential and the shape and height of lactation curves are affected by factors such as the number of consecutive lactations, age at parturition, season of calving⁵, gestation stage⁶, and length of previous dry period². The handling and feed systems used in different geographic zones, regions and countries can also have a significant effect on dairy cow milk production^7,8,9.

Many mathematical models have been used to describe lactation and estimate expected milk production². Some of these models focus on attaining the best fit for the mathematical equations and give less weight to lactation biology¹⁰, while others aim at improving understanding of biological processes¹¹.

When control day production data are fitted using empirical regression equations, different lactation curve shapes can be identified. Some are slight modifications of the standard (typical) curve, for instance, due to the presence or absence of inflection points in the descending portion of a lactation curve. Others can differ notably from the standard curve, such as curves that decline continually and have no lactation peak¹².

Most studies using lactation curves are focused on identifying the curve with the best fit among average curves. That with the best fit is then used to fit all the lactations in a data set. Applying these criteria to identify the best model often ignores statistical or biological problems that may occur when the fit is extended to individual lactations. This can result in inaccurate parameter estimation¹³.

In milk production genetic models, the primary concept is that animals can differ genetically, both in terms of total milk production and their lactation curve shape¹⁴. Variation in milk production curve shape occurs in different species^5,15. Given this variation, it is vital to find the most appropriate mathematical function that best describes each production situation¹⁶.

The present study objective was to apply four mathematical models to analyze and model individual lactation curves in the Siboney genotype of Cuba.

Material and methods

Data analyzed in this study were from Siboney cattle (5/8 Holstein, 3/8 Cuban Zebu) from Pinar del Río province, Cuba. This region has two clearly defined seasons: a rainy season from May to October with 70 to 80 % (960 mm) of yearly rainfall; and a dry season from November to April (240 mm). Average annual temperature is 23.1 °C, relative daytime humidity is 60 to 70 % and relative nighttime humidity is 80 to 90 %¹⁷.

A total of 31,631 test day milk yield (TDMY) records were analyzed from 3,697 monthly controlled lactations (first to fifth) in 2,632 cows born between 1987 and 1999. Feed system was daily grazing for approximately 12 h daily. Star grass and Guinea grass were the principal feed, although the cows also grazed naturally occurring grasses in the rainy season. The cows were milked twice daily, and provided a 0.45 kg concentrate supplement beginning at the fourth liter of milk produced. The cows were corralled at night and fed king grass (Penisetum purpureum) and sugar cane (Saccharum officinarum).

Lactation curves were modeled using four functions applied previously in this population to model average curves:

Wood¹⁰: Y_t = a.t^b.e^ct

Wilmink¹⁸: Y_t = a+be^-kt +ct

Ali and Schaeffer¹⁹: Y_t = a+b(t/330)+c(t/330)²+dlog(330/t)+k[log(330/t)]²

Fourth order, normalized Legendre orthogonal polynomials²⁰: Y_t ∝=₀ xP ₀+∝₁ xP ₁+∝₂ xP ₂+ ∝₃ xP ₃ + ∝₄ xP ₄

In all four models, Y_t is TDMY in time t, corresponding to lactation days at the time of milk weighing. Parameters a, b, and c are associated with production level, and parameter k is linked to time at peak lactation and is usually assumed to be fixed^18,21. In the Wilmink model, k= 0.10 was assumed²². Time functions (Pj) included in the models using Legendre polynomials were calculated with values published by Schaeffer²³.

Results

Average TDMY varied from 5.9 ± 3.3 to 3.7 ± 2.0 kg, with an overall mean of 4.9 ± 2.7 kg. Values for R² _A were >0.75 in 23 % of lactations using the Wood function, 24 % using the Wilmink function, 28 % with the Ali-Schaeffer function, and 36 % when using the Legendre polynomials function (Table 1). When R² _A curves >0.75 were selected, the three-parameter models identified four types of curves (Table 2). The Wood model identified more (61 %) standard curves than the Wilmink model (47 %).

Table 1 Absolute frequencies and relative percentages (in parentheses) of fits in different classes of fitted coefficients of determination (R2A). 

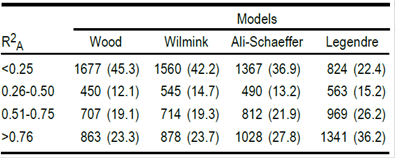
Table 2 Means and standard deviations of individual curve parameters classified according to the four shapes identified by the Wood and Wilmink models. 

§ Lactation curve shapes: 1= typical; 2= continuously descending (atypical); 3= reverse standard; 4= continuously increasing.

¶ sample size.

In curves modeled with the Wood function for increasing b values, estimates during the first lactation increased (Figure 1a), whereas in atypical curves increases in b did not persist (Figure 1b). With the Wilmink function, in contrast, the typical curves had a convex shape that was accentuated by negative b values (Figure 1c), whereas in atypical curves positive b values accentuated the curve’s concave shape (Figure 1d). This highlights the difference in meaning of the b parameter between the two curve groups within the same model, and confirms the link between b values and the variation rate in the first portion of the curve.

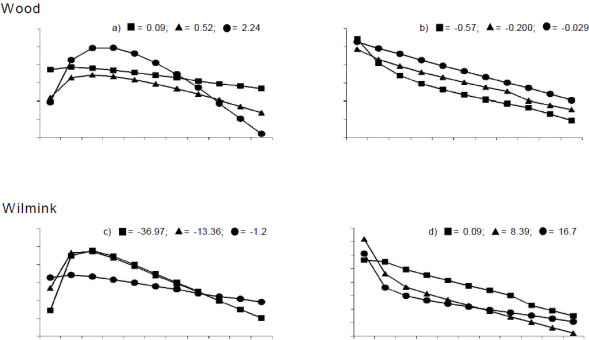
Figure 1 Typical (a and c) and atypical (b and d) lactation curve shapes identified by the Wood and Wilmink models; chosen for increasing b parameter values. DIM= days in milk; TDYM= test day yield milk. 

Of the 32 theoretically possible groups, the Ali-Schaeffer model identified 17 curve types and the Legendre polynomials model 20 types. Nonetheless, each group was essentially the result of a specific deformation of the two basic shapes (typical and atypical). Variability occurred in the form of inflexion points within the two curve groups. The four curve groups with the highest frequencies were included in the analysis (Table 3).

Table 3 Parameter distribution (mean ± standard deviation) of individual curves classified based on the four groups most frequently identified by the Ali-Schaeffer model. 

Estimates for individual curves were generated for each of the four main Ali-Schaeffer model curve groups (Figure 2). In group 1, the increase in parameter b represented a rise in milk production at the beginning of lactation (Figure 2a), whereas in group 2 an increase in b marked the decline rate of the curve’s initial portion. Inflexion points occurred in both groups at 60 d, a clear consequence of the high flexibility of five-parameter models, which can identify different rates of decreased or increased milk production throughout lactation. However, the opposite sign in the parameters means that the sequence of changes in curvature is the opposite in the two groups. The patterns in groups 3 (Figure 2c) and 4 (Figure 2d) are examples of different consequences in response to an increase in the b parameter. In group 3, the curvature in the second portion increased while in group 4 it tended to decline linearly.

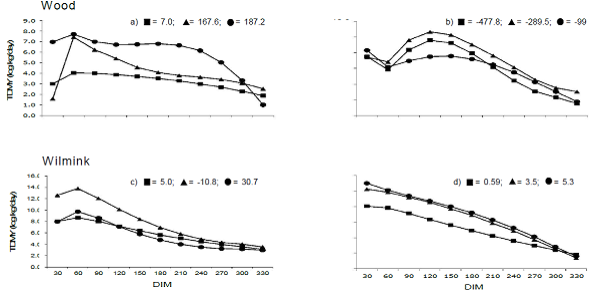
Figure 2 Examples of curve groups 1(a), 2 (b), 3 (c) and 4 (d) identified using the Ali-Schaeffer model, and selected for increasing b parameter values. DIM= days in milk; TDYM= Test day yield milk. 

Among the four groups identified using Legendre polynomials (Table 4), a contrast in signs was present between groups 1 and 2, except for parameter α0, which was positive in both. Individual curves were generated for the four main groups for increasing values beginning from the term α1 (Figure 3). In group 1, increase in the α1 parameter caused a decrease in curve level and an increase in its curvature, while in group 2 an increase in α1 resulted in a lower slope and a more stable curve. The same behavior in response to increasing α1 values was also observed in groups 3 and 4.

Table 4 Parameter distribution (mean ± standard deviation) of individual curves classified based on the four main groups identified by Legendre orthogonal polynomials 

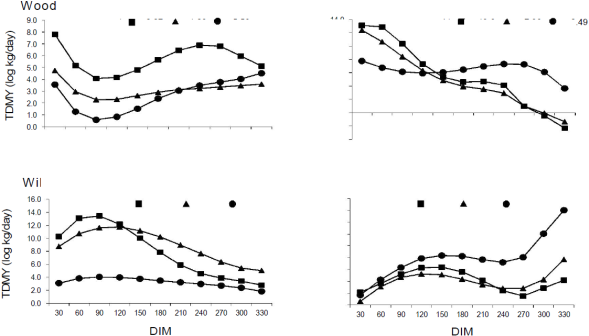
Figure 3 Examples of curve groups 1(a), 2 (b), 3 (c) and 4 (d) identified using Legendre orthogonal polynomials, and selected for increasing α₁ parameter values. DIM= Days in milk; TDYM= Test day yield milk 

Of the correlations calculated between estimated parameters for the first two groups classified as typical and atypical curves with the Wood and Wilmink models, most were significant (P <0.05). Of the correlations for the first two groups classified using the Ali-Schaeffer and Legendre polynomials models, significant (P<0.05) correlations were found in all but group 2 of the Legendre curves (Table 5).

Table 5 Correlations estimated between the parameters of the analyzed models 

* Not significant values (P>0.05).

Discussion

The TDMY values used in the present study were higher than those reported elsewhere for Siboney Cuba cattle^27,28. In a study of 1,041 lactations in this genotype, R² _A values >0.75 were found in 21 % of the lactations modeled with the Wood function and 39 % of those modeled with the Ali-Schaeffer function²⁷.

Goodness of fit increased with the number of parameters included in the function since this is related to model flexibility^21,29. However, the parameters used in polynomial functions do not necessarily have a clear relationship to the basic characteristics of lactation curve shape; this is particularly the case for high order polynomial functions³⁰. This makes biological interpretation difficult and leads to negative values at curve ends¹³.

The a parameter value estimated here with the Wood function for the typical lactation curve was lower than that reported for Holstein cattle³¹. This parameter’s scale is directly related to milk production level. The lower value in the present study was expected since, in terms of production traits, the selection program for the Siboney of Cuba genotype was designed to result in low input cattle for a tropical climate.

Compared to the Wood function, the outstanding element of the Wilmink function is the independence of the first and second portions of the curve. This is confirmed by the lower correlation value between b and c in both the typical and atypical curves. Macciotta et al²²⁾ suggested that interparameter dependence may be the reason the Wood model identifies more standard curves than the Wilmink function.

These two models are known to differ in their ability to describe lactation curve shapes³². According to the second derivative of the Wood function, the absolute value of b controls lactation pattern curvature magnitude, which is the deviation of a straight line²⁴. In other words, when b is positive the curve is concave and when it is negative the curve is convex.

Parameters generated with the Wood and Wilmink functions need to be analyzed with caution. A number of authors claim that the occurrence of peak less lactation curves is mainly due to results produced from records with no data for the first days of lactation. For example, the notable presence of negative b parameter values refers to lactations with initial TDMY weighings at 30 d or more after parturition²⁴. However, atypical curves are apparently not strictly linked to the day the first TDMY record is made³³.

Peakless lactation curves have been described in dairy cattle³¹, sheep³⁴, lambs²⁵, and buffaloes⁵. This may be a pattern characteristic of certain livestock breeds, including Siboney of Cuba, which has reported average lactation curves exhibiting a slightly flattened shape^28,35.

High correlation between parameters in the Ali-Schaeffer model means a change in curvature with increases in b, and is a known limitation of this model since it can obscure the estimation process, particularly in genetic analyses. Among other reasons, this has led to abandonment of the Ali-Schaeffer model in favor of Legendre polynomials²³.

Apparently, an end effect is common in the main groups containing negative estimated TDMY values at the ends of the lactation trajectory³⁷. As seen in group 2, this edge effect is characteristic of curves modeled with the Ali-Schaeffer and Legendre polynomials functions.

Using the Legendre polynomials model, the correlations between estimated parameters were lower than with the Ali-Schaeffer model. Schaeffer²³ mentioned this behavior, and considered it difficult to identify the biological reasons explaining why the Ali-Schaeffer and Legendre polynomials functions can detect different types of curves. However, this behavior is particularly useful in random regression analyses searching for individual deviations in an average fixed curve.

Conclusions and implications

Using control day production data for Siboney dairy cows of Cuba, the four main mathematical functions used to predict milk production throughout lactation generated different lactation curve shapes, particularly in the five-parameter models. This shape diversity reflects curve diversity within the herd. Treating them as derivatives of the two classic typical and atypical curve groups could compromise variability among curves, since analyses based on average curves do not reflect the individuality of lactation behavior in a population. Use of three-parameter models as submodels in variance component estimations using control day production data should therefore be done with caution.