1 . Introduction

Analog representation and computation play an important role in recent discussions in the philosophy of computation (^{Isaac 2018}; ^{Papayannopoulos 2020}; ^{Maley 2023}) and in the philosophy of cognitive science, particularly discussions of perception and core cognition (^{Carey 2009}; ^{Beck 2019}; ^{Clarke 2022}). Nevertheless, basic questions about the nature of analog representation have not yet been answered, including what, if anything, unifies the various types of paradigmatic analog representations. Consider two examples: a photograph of waves in the Atlantic Ocean, and a mercury thermometer reading 20 ^◦C. While both are analog, they have been classified differently by different theorists. The photograph counts as an iconic representation, often understood as a particular subtype of analog representation. The thermometer does not count as iconic, but an example of what are sometimes called analog magnitude representations (AMRs). What exactly is the difference between iconic and non-iconic analog representations, and what makes both a species of the type analog?

Understanding the answer to these questions -or at least how we might go about trying to answer them- may help shed light on recent discussions about analog representations, iconic represen-tations, and the so-called “Parts Principle”. According to the Parts Principle, iconic representations have parts that are themselves representations of what is represented by the whole (e.g., parts of a map -a representation of some terrain- are themselves representations of parts of that terrain). ^{Carey (2009)} , for example, argues that the AMR underlying elements of human core cognition has parts. On the other hand, ^{Peacocke (2019)} and ^{Clarke (2022)} note that some AMRs do not have parts at all, or only in an (at best) obscure way that does not support the Parts Principle. And on the third hand, ^{Kulvicki (2015)} argues that the Parts Principle is true of all analog representations, once we amend what counts as a “part” in terms of abstraction, rather than mereology. What then is the difference between analog representations that have parts and those that do not? Does having parts (or not) have any bearing on the type of representation in question, or what can be represented?

Progress toward clarifying these issues can be made by doing two things. The first task is to determine what the different types of analog representation have to do with one another; I will do this by extending and generalizing the account found in ^{Maley 2011} and ²⁰²³. The second task is to articulate the conditions under which any analog representation can be said to have parts; this requires a discussion of extensive and intensive magnitudes. Showing how the amended account then handles different types of analog representation -iconic and non-iconic, with and without parts- illuminates the dimensions along which they differ, while still having the right kind of variation to be analog in the first place.

A few notes are in order before we begin in earnest. First, much of the recent literature on analog representation has to do with its place in contemporary cognitive science, but my aim is to elucidate the nature of analog representation more generally. Whatever I say here had better be compatible with how cognitive scientists understand analog representation; if it is not, then so much the worse for what I say. Thus, my concerns (here, anyway) are not primarily with the extent to which various human cognitive and neural systems use analog representations, but with analog representation simpliciter.

Second, while it is still true that different accounts of what “analog” means -particularly relative to “digital”- can be found in the literature, the issues addressed here are only interesting for mirroring accounts of analog representation. The alternative account of the analog -the continuous conception- is, if not fatally flawed,¹ simply irrelevant to this discussion. I will focus on a particular mirroring account of analog representation (and, to some extent, computation) developed in ^{Maley 2011} and ²⁰²³, based on previous work by ^{Lewis (1971)} .

Third, although it is common use the term “content” for what is represented by a representation, I would like to avoid this term. This is simply because it comes with a decent amount of baggage from its use in the philosophy of mind. At the same time, discussing “the thing represented” is cumbersome. I will use the term “representatum” for whatever it is that is represented by a representation.

Finally, I simply assume that some things are representations, and that they represent other things. Nothing here is meant as a theory of representation per se, but simply a characterization of already-given representations. Thus, I will set aside the problem of representatum determination (i.e., the analog² of content determination) in what follows.

2 . Morphisms, Mapping, and Mirroring

The first thing we need to do is get clear on how to understand “mirroring”. In this section, I will expand on a particular mirroring account of analog representation, the Lewis-Maley account ^{(Lewis 1971}; ^{Maley 2011}, ²⁰²³⁾, and the one most consistent with the authors I will be engaging with later. Once we understand better what the mirroring relationship is in simple cases of analog representation, we can see how the idea generalizes to more complicated cases.

As a first step toward making “mirroring” more precise, one might take the relationship between a representation (R) and what it represents (S) to be an isomorphism: changes in S are reflected by corresponding changes in R. ^{Lee, Myers, and Rabin (2022)} , for example, take isomorphism to be the right relationship to characterize analog representation, modulo some degree of deviation (e.g., if a mapping is isomorphic except for one place, it is almost analog; a bit less for two places, etc., in a way that can be quantified). Similarly, ^{Burge (2018)} articulates an isomorphic view of specifically iconic representations. However, ^{Shagrir (2022, p. 232)} has noted that isomorphism is too strong, for two supposed reasons. First, isomorphism is a symmetric relationship, but representation is asymmetric. The height of the liquid in an analog thermometer represents the temperature, but the temperature does not represent the height of the liquid. Second, isomorphism is transitive, but representation is not. Thus, if the domain of R is isomorphic to S, and S is isomorphic to other domains (which is virtually guaranteed), then R is isomorphic to these other domains. This means that R not only represents S, but all of the other things to which S is isomorphic.

Shagrir is right to reject isomorphism as the way to characterize analog representation (contra ^{Lee, Myers, and Rabin (2022)} ), but for the wrong reasons. Let us see why Shagrir’s concerns are unfounded, which will then help clarify why we should reject isomorphisms in favor of homomorphisms.

What we want is a characterization of the relationship between representations and what they represent. This relationship is only important in one direction, as it were: from representata to representations. Thus, what we want is a function, or mapping, and not a relation.³ Let us call this function from representata to representations m; thus m: S → R. Suppose for a moment that m is an isomorphism: thus, every element of S maps onto an element of R, and every element of R has some element of S that maps onto it. Furthermore, m is structure-preserving, meaning that the structure of S is reflected in the structure of R. In other words, one or more relations among the elements of S are preserved when those same elements are mapped to R. This will be specified in more detail later; for now, a simple example suffices. If we have two temperatures t ₁ and t ₂, where (t ₁ < t ₂), and two heights of liquid a and b in a mercury thermometer, where a represents t ₁ and b represents t ₂, then (a < b). The “less than” relation among temperatures is preserved when the temperatures are mapped to heights by the corresponding “less than” relation among those heights.

Our mapping m is meant to capture the fact that temperatures (elements of S) are represented by heights of liquid (elements of R), and relationships among the magnitudes of the temperatures are reflected in relationships among the magnitudes of heights. However, the fact that m is isomorphic does not mean that the mapping goes in the other direction, such that temperatures represent heights of liquids; that is simply not the way that this mapping is defined. The function m is from representata (i.e., temperatures) to representations (i.e., heights). Now, there exists an inverse mapping that goes the other way, mapping heights to temperatures. However, that is simply a different mapping, and not one we are concerned with.

Similarly, there are isomorphic mappings from many other things to temperatures, such as the unread books on the shelves of a university’s library, or from the ounces of coffee I drink every day. Let us call the function from unread books in some particular library to temperatures n; let us suppose it, too, is isomorphic. Thus, the function n maps book-counts to temperatures, and m maps temperatures to liquid heights. Does that mean that liquid-heights then represent book-counts? No. We could compose the functions m and n to create yet another function mapping liquid-heights to book-counts. But the mere fact that the function m is isomorphic with n does not imply any transitivity of representation.

In short, there has been some confusion about what follows from the fact that a function is isomorphic. Given an isomorphic mapping like m, we know that there must be an inverse mapping. But that does not mean that m itself is symmetric; in fact, that is a category mistake. Relations, such as less-than or equal-to, are candidates for symmetry (as well as transitivity, reflexivity, and the like). The fact that some symmetric relation holds between h and j necessarily means that it also holds between j and h. Functions, however, are not relations.

We can now see that these concerns about characterizing representation in terms of isomorphic functions are unfounded. However, there are two other, separate problems with isomorphisms. First, there is a point made by ^{Krantz et al. (1971)} :⁴ an isomorphism strictly implies that if y and z represent the same thing, then y and z must be numerically identical. For example, suppose y is a representation of the number five by some length, say in a slide rule; z is also a representation of five by a length in a slide rule. We do not want it to follow that y and z must be the very same lengths of the very same slide rule. Rather, we want it to be the case -or at least, possible- that y and z are parts of different slide rules that happen to have the same length. But this is simply not allowable under a one-to-one mapping.

The other problem is that isomorphism does not adequately capture many clear examples of analog representation. Recall again our function m: S → R. It is a one-to-one mapping, meaning that every element of R maps onto an element of S, and every element of S has some element of R that maps onto it. Now, consider the second hand of an analog watch that ticks in discrete steps, once per second. Here, R is a set of points in time, and S is the set of 60 positions of the watch face.

If we insist that the mapping must be an isomorphism, as in ^{Lee, Myers, and Rabin 2022}, then the cardinalities of R and S will have to be the same. The cardinality of R is fixed: there must be 60 elements, one for each position of the discrete, ticking second hand. Thus, S will have to have 60 elements as well. But this is a bit strange: we know that time itself is not broken into discrete, one-second units; that is simply a convenient way we measure and represent time for many everyday purposes. So what are the units of time? This is an empirical question (or so I suppose), and one whose answer is not yet settled. From what I understand, one candidate is the Planck time constant, roughly 5.34×10⁻⁴⁴s. Or, perhaps time is really continuous, not divisible into units in the way it would be if it were discrete. In either case, there are going to be many more elements in S than in R, and from that it follows that there simply can be no one-to-one functions, and thus no isomorphic functions from R to S.

There are two solutions, each of which involves grouping together sets of times. First, rather than mapping individual units of time (elements in S) to individual representations (elements in R), sets of times (sets of elements in S) could be mapped to individual representations. For simplicity, suppose we consider all of time between two ticks as being represented by the “lower” or “first” tick. All times between the 15th and 16th tick of the dial will be mapped from the 15th tick. So the actual time (as it were) of 15.23. . . seconds is represented by the hand being at the 15th tick mark (however it happens to be labeled, or even not labeled, as on a blank watch face). If that is unsatisfactory, instead of rounding up, we could round to the nearest whole number. Thus, we could map all times between 14.5 seconds and 15.5 seconds to the 15th tick mark. In any case, we must map sets of times to individual representations.

Rather than an isomorphism, this function would be a homomorphism: it is not one-to-one, but many-to-one. The difference between the two is visualized in Figure 1. Every element in R represents some set of times, shown by the sets in S mapped to individual elements of R. This may seem to introduce some ambiguity because it suggests that each position of the second hand simultaneously represents a huge number of individual times, which is counterintuitive. However, the solution is straightforward: take the sets of elements mapped onto a single representation as an equivalence class. After all, for the everyday purposes for which we use the second hands of clocks, it is usually fine to treat all of these times as more-or-less equivalent. When they cannot be so treated, we simply use a clock with a higher resolution: perhaps a stopwatch that measures times in milliseconds. In this case, R has 60,000 elements instead of 60, and the equivalence class will consist of times that are much closer to one another, but otherwise the idea is exactly the same.

Figure 1 Generic mappings of an isomorphism (left) and homomorphisms (center and right). 

The second solution is to consider the sets of times in S as the thing to which elements of R are mapped. Thus, the elements of S are themselves sets of individual times, which each of which is mapped to an element of R. This may have the benefit of preserving the idea that a given representation has only one representatum. After all, we typically take the second hand pointing to the numeral “3” (or “III”, or at a 90-degree angle from vertical in the clockwise direction, or whatever) on a clock to represent 15 seconds full stop;⁵ not simultaneously 15 seconds, 15.2 seconds, 14.9 seconds, 15.06 seconds, and so on. Thus, it might be better to stipulate that S is an isomorphism after all: S would have exactly as many elements as R, so that the second hand in the example represents the set of times that includes 15 seconds.

The difference between these two solutions is subtle, and it is not clear which is to be preferred -perhaps different ones are better in different contexts. In any case, with discrete analog representations such as these, it is important to make clear that representations with different resolutions can represent the same thing. A stopwatch with single-second resolution represents the very same thing as one with a thousandth-second resolution. Moreover, that resolution is not a property of what is being represented, but of the type of representation we are using. Time is whatever is, whether continuous or discrete; but we represent it (at least sometimes) with the discrete ticks of a clock’s second hand.

These considerations should make it clear that isomorphism is not enough to capture many analog representations; we need some way of capturing many-to-one mappings in these two different ways. Using homomorphisms, rather than isomorphisms, works perfectly. However, more than mere mapping is required for a morphism: there must be a preservation of structure. To illustrate, if we take literally the vertical arrangement of the elements in Figure 1, there is an “above” relation among those elements. So, for example, r ₁ is above r ₂, which is above r ₃, and so on. Same for s ₁, s ₂, . . . As it happens, this relation is asymmetric, transitive, irreflexive, and -most importantly- preserved in the mapping from S to R. In other words, let the element r ∈ R that a given element s ∈ S maps onto be denoted by m (s) = r. Let us use ↑ to denote the relation “is above” (e.g., s ₁ ↑ s ₂, r ₁ ↑ r ₂, etc.). The function m is a homomorphism in virtue of the fact that, if s _j ↑ s _k , then m s _j ↑ m (s _k ), i.e., r ₁ ↑ r ₂. In real examples, the relation of interest between elements of S will be a relation among a physical property of the elements of S. More about this will be said below.

3 . Dimensions of Representations

In a recent paper on analog computation and representation, ^{Maley (2023)} characterizes analog representation as follows:

A representation R of a quantity Q is analog (with resolution r) iff:

In plain English, the idea is that the property of a representation that is doing the representing increases/decreases as the representatum increases/decreases. Of all the properties of a liquid thermometer, it is the height of the liquid that does the representing. Moreover, the literal increase/decrease in that height represents an increase/decrease in temperature (i.e., monotonic covariance between representation and representatum). A liquid height of 34 mm that represents 34 ^◦C is literally taller (i.e., larger in magnitude) than a height of 33 mm that represents 33 ^◦C (and, of course, 34 ^◦C is larger in magnitude than 33 ^◦C). This is in contrast to, for example, digital representation, where the physical properties of the digits involved need not monotonically covary at all. In a digital thermometer, a LED display of the two digits “33” is no bigger, smaller, taller, or anything else than the two digits “34”: they are simply different. Of course, they could be larger, taller, or whatever, in some particular scheme; but that is not a necessary part of digital representation. All that’s needed is that the symbols differ in ways we can interpret according to the conventions of digital representation (this is discussed in more detail in ^{Maley 2011}).

This is all fine as far as it goes, but, like mirroring, it can be made clearer. How can we best understand “covariation” between analog representations and their representata? In other words: with respect to what is it that they vary? With an answer in hand, we can see one way in which different kinds of analog representation are, in fact, unified; later, this will help us to understand how the “Parts Principle” does and does not apply to different analog representations.

Let us focus again on the liquid thermometer, even more closely. As just mentioned, these thermometers represent temperature by the height of a liquid in a narrow glass tube. More specifically, they represent the temperature at the tip of the thermometer, a particular point (or very small volume, anyway) in space. When we say that the height (the representation) varies monotonically with the temperature (the representatum), we mean the temperature at that point. Moreover, when we say that the temperature varies, we mean that it varies, at that point, with respect to time. We could move the thermometer around; we could keep it in one place. In either case, as time passes, any increase in temperature at that point will result in an increase in liquid height. If we were to plot these increases on the same graph, we would get something like Figure 2.

Figure 2 Temperature increases and height increases with respect to time. 

A graph like the one in Figure 2 would typically be most useful if the temperature being displayed were the temperature at a fixed location; showing, for example, the effects of a heat lamp turning on and off in a laboratory setting. If the displayed temperature is from a thermometer that is being moved around as time passes, this graph would need more information to be useful. In any case, it is a certain point on the thermometer that varies in height, according to the temperature, as a function of time.

Although I am hesitant to introduce more terminology, it does help to make clear how precisely analog representation works. There are three components worth tracking. First, we have the representatum, which we can also think of as a dependent variable -it is the thing that varies, and the thing that is to be represented in the first place. In this example, it is temperature. Second, we have the representation, which is the thing that represents the representatum; in this example, the height of the liquid. Finally, we have an independent variable: whatever it is such that, with respect to it, the representatum, and thus the representation, vary. In this case, the independent variable is time. The plot of the variation in the representation and representatum in Figure 2 are precisely variations with respect to time.

In the case of this analog thermometer, this is all quite obvious once we go to the trouble of laying it all out; it is not yet clear what all that trouble is worth. More will come in the next section, but for now, showing how different types of analog representation fit this tripartite scheme makes clear how these different types are actually unified in a non-obvious way. Let us look at another example.

Consider an hourglass, an analog timer. Here the representatum is time, and the representation is the amount of sand. We could plot this as well, but it would be rather boring: both the representation and representatum would be straight, parallel lines (with some positive slope). Why? Because in this case, the representatum varies constantly, and the representation correlates linearly with the representatum. But what exactly is the independent variable in this case? That is, with respect to what does the representatum, and hence the representation, vary? Odd as it initially sounds, in this case, the independent and the dependent variable -the representatum- are the same: time. After all, as the amount of time elapsed increases, so does the amount of sand in the bottom of the hourglass. In this case, however, we are treating the independent variable as the thing to be represented, and thus it is also the dependent variable. It does not seem correct to say that we are representing time with respect to time; so let’s not say that.⁶ We will simply say that our independent and dependent variable are the same.

Both of these are examples of what we might call one-dimensional representations. We have one independent dimension, and one dimension of what is represented (the representatum). Variation in the representatum is a function of the independent variable (which is what allows plots like Figure 2 to make sense at all). Let us look at two more examples before moving on to two-dimensional representations.

Electronic analog computers typically represent the values of variables by the voltage across some circuit element. So, seven is represented by seven volts. This is in contrast to electronic digital computers, where one of two voltages (typically zero and five volts) represent one of two binary digits (0 and 1), and the sequence of these digits represents the value of a variable (^{Maley 2011}, ²⁰²³). In one sense, an analog element is much like the thermometer from above: as the representatum increases (or decreases), the representation increases (or decreases), and that variation happens across time. There are two important differences, however. First, unlike the thermometer, the value of the representatum is not determined by sensing some property of the environment: it is an element of a computational system, set by either the user of the system, or some other element of that same system.⁷ Second, the representatum need not have any units: it may be that a value of seven volts represents the number seven (and not seven meters, seven kilograms, etc.). In fact, even if there are units involved in a particular problem (e.g., a computation is being performed to determine the average mass of a set of objects), it is clearer to maintain that the elements in the computer represent numbers, and those numbers represent (for example) the number of kilograms in the problem. That is a subtle issue that we need not resolve here.⁸

Finally, consider a vinyl record (to keep things simple, we will only consider a monophonic record; stereo records are essentially just two monophonic records played simultaneously, one in each channel). Records represent sound by the physical variation in the peaks and valleys (the heights and “frequencies”) of the groove.⁹ The needle vibrates as it contacts these peaks and valleys, and that vibration is amplified to produce sound. The peaks and valleys are nearly-linearly correlated with the peaks and valleys of the sound that has been recorded, so much so that one can “play” a record with only a pin taped to a cone of rolled-up paper: no fancy decoding equipment is necessary, as in the case of a digital recording. Now, this representation is a bit complicated, because although the representation and representatum vary with time, they are also only defined over a duration. In other words, a note such as middle C has a frequency of 261 Hz, but there is no note without at least a small duration of time. However, we can set this complication aside, and refer to an instantaneous frequency if need be, the same way we can refer to instantaneous speeds.

So much for one-dimensional representations: let us look at two dimensions. A canonical example of a two-dimensional analog representation is a photograph; for simplicity, let us start with black-and-white ones (more properly, greyscale). In this type of representation, there are two independent dimensions of variation (the two spatial dimensions of the photograph), and one dimension of what is represented.¹⁰ So, to be clear, the representatum is an image, the representation is the photo, and there are two independent dimensions. Like the one-dimensional cases, this seems like a clear case of a mirroring relation. But how can we extend the one-dimensional case so that it works for this kind of analog representation?

Like the one-dimensional case, we have to think about variation along the independent variable -except now there are two of them. At any point in the photo, the grey level at that point represents the grey level at the corresponding point in the representatum. If we move in either the up-down or left-right direction (i.e., the two dimensions of variation), an increase/decrease in the gray-level of the representatum will be represented by an increase/decrease in the grey level at the corresponding point in the representation (i.e., the photograph). In fact, we could move in any combination of the two dimensions of variation: we need not move only up-down or left-right. Moreover, we can plot the grey levels of the representatum and the representation as we move in some direction just as we did for the thermometer; this is depicted in Figure 3.

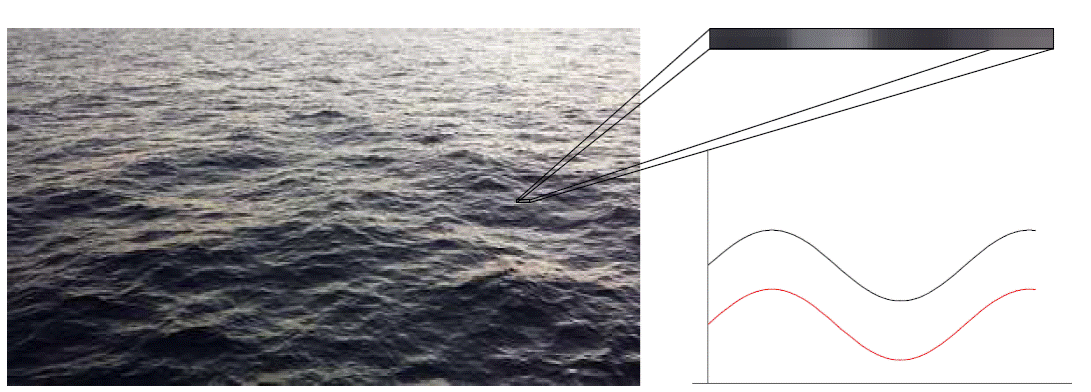
Figure 3 Photograph of waves, depicting actual waves. Zooming in on a small line segment shows how we can move along the independent variable(s), and get covariation between what is represented (the gray levels of the waves) and the representation (the photograph). 

When we make explicit the dependent variable (the representatum) and the representation, we see that the representatum and representation are of the same type. What we are representing is the gray levels of the waves as seen from some particular point of view. How we are representing these grey levels is via the grey levels of points on a photograph. Now, these may or may not be the very same gray levels; in fact, they are probably not. But we are representing color by color (or brightness by brightness in the greyscale case). A different kind of two-dimensional analog representation could instead represent brightness by the heights of a surface, so that lighter colors are higher than darker colors.

Also, notice that in the graph on the right side of Figure 3, the independent variable is not time, but the change in location for the left-right spatial dimension. Additionally, the line graph of the variation in the gray levels of the image and in the photograph are depicted as smooth curves just for convenience; because there are individual pixels, the actual graph would be a discrete step function.

Other examples of two-dimensional analog representations include maps and plots of functions of two variables. Of course, maps often include non-analog information, such as arbitrary color-coding to convey differences in types of roads, but they are still fundamentally analog. Additionally, there are still higher-dimension analog representations. A movie of waves, for example, would have three dimensions of variation (two spatial dimensions and one time dimension), and thus be three-dimensional. A scale model would have three spatial dimensions of variation, and thus also be three-dimensional, but in a different way. A 3D-animation of a storm over time would be a four-dimensional representation (three spatial and one time dimension). We need not walk through each of these examples; the point is simply that the basic structure of analog representation applies to each of these, and what counts as variation in the different types of representation is made clear when we carefully track the dimensions of variation in each.

What about the structure-preserving aspect of multidimensional analog representation? This aspect generalizes from the one-dimensional case, too -we simply need to think of the relevant homomorphisms across multiple dimensions. Like other elements of this analysis, the fact that this happens so readily in everyday examples makes the precise characterization seem tedious. However, the tedium will be useful.

Consider the photograph, which we just noted has two independent dimensions and a single dependent one. We have already discussed the covariance between the points on the photograph and the points of the image: the lighter-darker relation that holds among the greyscale levels of the image is preserved in the lighter-darker relation among the greyscale levels of the photograph. However, the spatial structure of the points in the image is also preserved in the spatial structure of the points in the photograph. Suppose we have two points, p ₁ and p ₂ in the image, represented by points q ₁ and q ₂ in the photograph. If p ₁ is above p ₂, then q ₁ will be above q ₂. The structure is two-dimensional, however, so the same will be true if we replace “above” with “left of”. The idea is intuitive enough, but perhaps worth illustrating a bit more.

As in the case of the thermometer, we have a homomorphism between the representatum and representation, mapping grey levels to grey levels, and which preserves the darker-lighter structure. In addition, we have a homomorphism between points on the representatum and points on the representation. It is most natural to think of these in terms of two two-dimensional grids, where points are mapped to each other in just the way one would expect.¹¹ In this case, there are two separate relations that are preserved: the above-below relation and the left-right relation, exactly as mentioned above. Thus, we have the preservation of three separate relations: the light-dark relation of the points of the image, and the spatial structure of those points. This is illustrated in Figure 4.

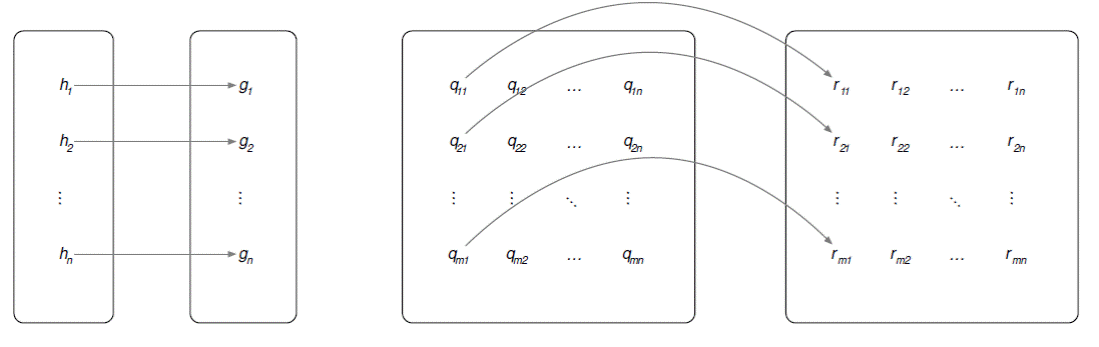
Figure 4 Homomorphism between image points and photograph points (left) and between spatial location of those points (right). Only a few arrows are shown on the right for clarity. 

One might wonder why we had only one relation to preserve in the one-dimensional example of temperature, but three in the two-dimensional case. Why did we add two additional relations, but only one dimension? In fact, in the one-dimensional case, there really are two separate homomorphisms preserving two separate relations, but we did not make it explicit. The independent variable in that case is temporal structure instead of spatial structure; we assumed that the time at which a thermometer indicates a particular temperature corresponds to the very time at which it is that temperature. For most purposes, this is a fine assumption, not worth making explicit. However, for other purposes, it may be good to make this explicit. For example, thermometers do not instantaneously change when temperatures change: it takes some amount of time for the liquid (or whatever) to physically move to the right place. If the temperature suddenly increases sharply, it may take a few seconds for the thermometer to reflect that change. Thus, it would not be correct to say that the point in time at which a thermometer indicates a temperature correspond to the very same point in time at which it is that temperature: some delay will be needed, which could be reflected in the appropriate homomorphism. Nevertheless, the structure of points in time (i.e., the “earlier than” relation) will be preserved.

Once again, the idea here can be generalized to more dimensions: three spatial dimensions are preserved in scale models; two spatial and a temporal dimension are preserved in animations. In fact, there is a strong case to be made that, understood in this way, the class of representations commonly known as “structural representations” are nothing more than analog representations. However, fleshing out this idea will have to be a task for another time.

One final point should be made about static analog representations, such as bar graphs, which do not vary at all.¹² In a bar graph, some value is represented by the height of a bar; however, these are typically static images, so there is no variation. It might seem that the analysis provided here cannot be applied to such a case. A full treatment would take us too far afield, but the basic idea is that the variation is counterfactual: if the value would have been higher, then the bar representing the value would have been taller. In fact, we cannot understand any single representation as analog without considering what it would do if the representatum were to vary. If we have stipulated that a particular bar graph is an analog representation, then it cannot be the case that, were the representatum to steadily increase, the height of the bar would change in arbitrary ways. If it is analog, then the height of the bar would increase as the representatum increases.

The last two sections have spelled out, in some detail, what makes a given representation analog, and what higher-dimensional analog representations -which may be what other call structural representations- have in common with simple one-dimensional representations. Besides adding some precision to our understanding of analog representation, this account allows us to get clearer on the different notions of “parts” of analog representations, the subject of the next section.

4 . Parts of Analog Representations

Some analog representations have the interesting feature that their parts are themselves representations: those parts represent parts of what was originally represented by the whole. One can take a photograph of a cat, cut out a part that contains just the ears, and then have a photograph of the ears of that cat. This is not true of representations in general: the “w” in “Antwerp” does not represent some part of the city, and none of the three lines that are part of “π” represent anything at all. Moreover, this feature is not true of all analog representations either: the height of the liquid in an analog thermometer represents temperature, but a part of that liquid doesnot represent part of the temperature. But for iconic analog representations, this feature is taken to be necessary (^{Clarke 2022}). We can codify this feature, often called the Parts Principle, as follows:

The parts of an analog representation of S are representations of parts of S.

In this section, I will make clear, in a principled way, why certain analog representations admit of the Parts Principle and others do not. By illustrating a difference in the types of magnitudes involved in analog representations, we will see that the Parts Principle may not be that important after all. As Clarke argues, what matters more is that we are clear about analog representation more generally, whether iconic or not (^{Clarke 2022, p. 16}). First we will see that the types of magnitudes involved determine whether the notion of “part” is applicable at all. Then, using the discussion of dimensions of variation from above, we will see how considering different types of magnitudes applies to the different ways a given representation can be partitioned.

The core of analog representation is the “representation of magnitudes, by magnitudes” (^{Peacocke 2019, p. 52}). While true, it turns out that not all magnitudes are created equal. The extensive magnitudes roughly correspond to physical quantities: length and mass are examples. The intensive magnitudes roughly correspond to physical qualities: temperature and color are examples. Kant was perhaps the first to make this distinction explicit, and in fact formulated extensive magnitudes as those “in which the representation of the parts makes possible the representation of the whole,” (^{Kant 1988, p. A162/B203}). This is nearly the Parts Principle, except Kant was speaking of the mental representation of extensive magnitudes, rather than representations using extensive magnitudes. However, the combining of parts is essential in both cases.

Extensive magnitudes are thought to have two closely-related features. First, there is way of physically “adding” magnitudes. What this means is that, given two magnitudes with values v and w, there is a physical operation that corresponds to mathematical addition, which means that the result of the operation is a magnitude of (v + w). For instance, a length of 33 mm can be added to a length of 34 mm in the obvious way: concatenating the lengths, resulting in a length of 67 mm. Second, extensive magnitudes can be partitioned in ways that correspond to an intuitive notion of parts. A length of 67 mm has, as parts, 33 mm and 34 mm lengths (as well as infinitely many other partitions of lengths). Mass can be treated similarly: masses can be added and divided in obvious ways. It seems that the ability to be partitioned goes hand-in-hand with the ability of parts to be physically added; we will return to this point below.

Non-extensive, or intensive, magnitudes are those for which there is no physical addition operation, and which do not have parts. Temperature is one example. Take two objects (or substances, or whatever) with temperatures e and f ; in general, no way of combining them will result in something with temperature (e + f ).¹³ Furthermore, a temperature of, say, 20 ^◦C does not have temperatures 15 ^◦C and 5 ^◦C as parts. Other examples of intensive magnitudes include density and hardness, which also do not admit of either partitioning or physical addition.

Noting this difference between extensive and intensive magnitudes makes clear why certain examples in the literature on analog and iconic representation do or do not admit of the Parts Principle. ^{Carey (2009)} uses the example of line length as an analog magnitude representation. Length is extensive (thus having parts, as just mentioned), and Carey concludes that representation by magnitudes is, in general, enough for Parts Principle to hold. ^{Clarke (2022)} notes that other magnitudes, such as speed, do not have parts, and thus it is too hasty to generalize from length. Speed is, of course, intensive: a speed of 45 m/s does not have 20 m/s (or any other speed) as parts. ^{Peacocke (2019)} makes a similar point, noting that representation by the firing rate of a neuron would also falsify Carey’s general claim. A neuron firing at 70 Hz does not have 10 Hz as a part -not even as a temporal part, as Peacocke notes. This is because frequency is an intensive magnitude.

Thus, the points made by Clarke and Peacocke can be generalized. Rather than examining individual cases, such as speed and frequency, we can state that, in general, Parts Principle holds for analog representations that use extensive magnitudes, and it does not hold for analog representations that use intensive magnitudes. Suppose I want to represent the number of days elapsed since my last birthday. Representing that quantity by a length of string in inches will result in an analog representation that has parts: each inch represents one day. Representing the same quantity by the temperature of water in a coffee mug will result in an analog representation that does not have parts: the temperature increases as the number of days increases, but there is no such thing as a part of a temperature.

We can further generalize this point to represented magnitudes. Suppose we represent an intensive magnitude with an extensive magnitude: a liquid thermometer is a common example. We have then an interesting case: our representation has parts, but our representatum does not. A column of mercury has a height, and height is an extensive magnitude -we can partition the height however we’d like. However, because temperature is intensive, it does not have parts. So what do the parts of the representation represent, given that the representatum does not have parts at all?

The simplest answer is that the parts of the representation do not represent anything. To be sure, a part is what the representatum would be if that particular part were considered as a whole. Similarly, they have the value that determines what the resulting representatum would be if that part were added (or subtracted) from the whole representation. This is somewhat subtle, so an example is helpful.

Suppose a thermometer with a liquid height of 70 mm represents 70 ^◦C. The representation -the height of liquid- can be partitioned in any number of ways, but let us consider a part with height 10 mm. It may be tempting to say that this part represents part of the temperature: 10 ^◦C, in particular. But because temperature is intensive, it has no parts, and thus this cannot be right. However, the 10 mm part is a representation of what the liquid height would be if the temperature were 10 ^◦C. Further, the 10 mm part is what would need to be added to the 70 mm representation to represent an increase in temperature by 10 ^◦C.

In short, while intensive magnitudes do not have parts, they can be represented by extensive magnitudes that do have parts. Although those parts cannot be said to represent the parts of the representatum (because there are no such things), those parts can be understood as the kind of thing that can be added and subtracted in order to represent other values of the representatum.

The reverse situation -using an intensive magnitude to represent an extensive one- is not only possible, but common. Real-world examples are found in neuroscience, where an extensive magnitude, such as weight exerted on a muscle, or the angle of a joint, is represented by a neural firing rate. In these cases, as the relevant part of the stimulus increases, the firing rate of the relevant neuron (or group of neurons) increases. As Peacocke states explicitly, neural firing rates are intensive: “A firing of fifty times per second does not have a firing of seventeen times per second as a part (not even as a temporal part)” (^{Peacocke 2019, p. 58}). Nevertheless, a firing of fifty times per second may well represent a mass of 50 g, or an angle of 50 ^◦. We then find ourselves in a similar situation as above, but reversed: the representation has no parts, but what is represented does. What can thus be said about the firing rate of seventeen times per second, given that it is not a part of fifty times per second?

Again, while it is true that no sense can be made of the idea that frequencies have parts, we can make sense of the relationship between a frequency of one magnitude (e.g., 17 Hz) and another (50 Hz). This is just the frequency that the neuron would fire if the represented quantity were 17 g (or 17 ^◦). It is also the decrease in the magnitude of the representation were the represented magnitude to decrease by 17 units. Or, equivalently, it is the amount by which the representation would decrease if a 17-unit part were taken away from the representatum.

We can now see exactly where Parts Principle applies and where it does not. When magnitudes are extensive, the magnitudes have parts, so when we have an extensive magnitude representing another extensive magnitude, then Parts Principle applies, and we have a clear case of iconic representation. When one or more of the magnitudes involved are intensive, then those magnitudes do not have parts, and the Parts Principle does not apply, and the representation in question is not iconic. However, as we see from the cases above, it is not clear why this matters. For those cases in which one of the magnitudes involved does not have parts, we can nevertheless make sense of what smaller (or larger) magnitudes are in the context of analog representation.

Things get more complicated in one sense, yet simpler in another, when we note that the distinction between intensive and extensive magnitudes is neither exhaustive nor basic. One could easily use magnitudes that are neither intensive nor extensive, such as the square root of mass. Square roots of masses can be combined, but the result does not map to addition, but neither does the combination amount to no change at all (as it would for say, color or temperature). More interestingly for our purposes, some magnitudes do not have parts in any intuitive sense, and thus may seem intensive, yet do admit of physical addition. Voltage is such a magnitude: 5 V does not have 2 V and 3 V as parts, but one can easily add 2 V and 3 V in a series to obtain 5 V. Moreover, whether the addition of voltage acts in an intensive or extensive way is context-dependent. As just mentioned, voltages added in a series combine in an extensive way; yet when added in parallel, they do not (as illustrated in Figure 5). Electrical current, however, is exactly the opposite: it is intensive in a series, but extensive in parallel (^{Redlich 1970}).

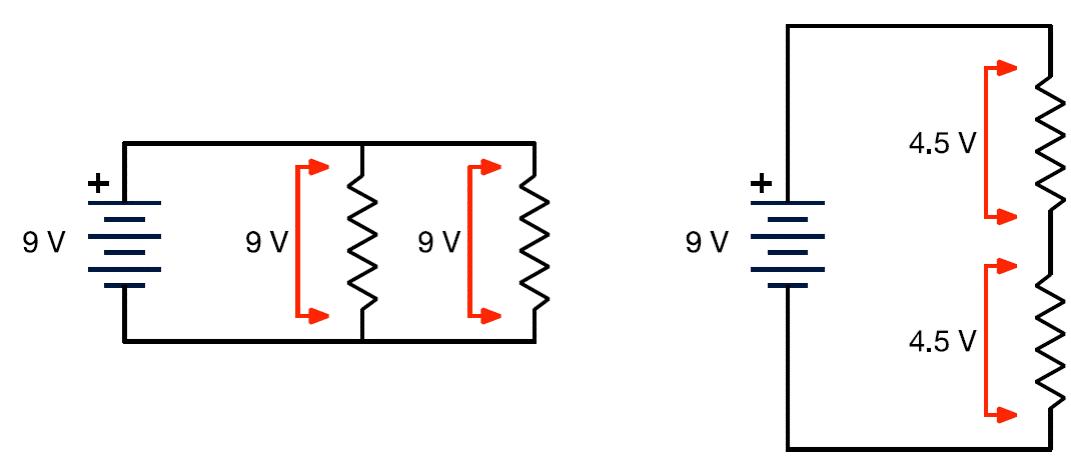
Figure 5 Physically adding voltages in parallel (left) and in series (right). With a 9 V battery, the voltage across parallel elements (here, resistors) is the same as the voltage across the battery: voltages do not add. Voltages across elements in a series, however, sum to the voltage of the battery: voltages do add in this case. 

The moral here is that we can make sense of which analog representations have parts (and why) by tracking which magnitudes are extensive, but that it may not matter whether smaller magnitudes are really “parts” in a strict sense, given that we can make sense of what smaller magnitudes are relative to other magnitudes. The point just mentioned about the complications regarding the intensive/extensive distinction pushes the point further still: what matters most is not whether magnitudes have parts, nor whether they are intensive or extensive, but whether there is an interpretation of smaller magnitudes that work as if they were parts.

Finally, considering the types of magnitudes involved in analog representations in the context of the dimensions of variation discussion from section 4 helps us get a grip on what parts of particular representations could be in multidimensional cases. For example, consider a photograph, this time in color. A part of a photograph is simply a subset of the whole photograph -a restriction of its height and width- illustrated in the top of Figure 6. Height and length are themselves extensive magnitudes, so it is perfectly clear what a part of a photograph would be along these dimensions. On the other hand, the colors that constitute the dependent variation are not extensive-they do not have parts, and we cannot take restrictions of this variation as parts of the original photograph.

Figure 6 Top: Original photograph on left, and a part of it on the right, obtained by taking subsets of the independent dimensions of variation. Bottom: Subsets of the dependent variable result in the red, green, and blue elements of individual pixels. 

However, we can understand what it would be to take certain restrictions on the dependent dimension of variation -the colors of the points. For instance, from an original photograph, we could create three new representations: one for each of the red, green, and blue values of the individual points; examples are illustrated in the bottom of Figure 6. Because color is not extensive, these would not be parts in a strict sense. Now, one might be tempted to say that they are parts: they are the parts of the colors of the individual points. Perhaps, but in whatever sense these might be parts, they are not representations of the colors of the points in the represented image. In other words, they are not parts in any sense that makes Parts Principle true. However, we know exactly what it would mean to combine these to get back the original photograph, because we understand what it is to “add” color values and superimpose images.

In fact, this is a way of making more precise how the point made by ^{Kulvicki (2015)} applies in certain examples. On his view, what is interesting and explanatorily unique about analog representations requires a generalization of what should count as a “part.” Kulvicki argues we should understand the “parts” of the Parts Principle to be abstractions of representations, rather than parts properly understood. Whereas it may be true that, in a strict sense, the parts of the height of the liquid in a mercury thermometer do not represent parts of the temperature, an abstraction of the liquid height represents an abstraction of the temperature. If we consider the height of the liquid in a thermometer to be at some particular level, it represents some particular temperature. But we can also take the height to be something like “between 70 and 80 mm”, which then represents a temperature between 70 ^◦C and 80 ^◦C. Similarly for photos: a lower-resolution version of a photo is a representation of the same image as the original, just at a lower resolution. Thus, in this case, Kulvicki would agree that the restrictions of color values of the photograph do not count as parts, but as a kind of abstraction.

Making clear the distinction between independent and dependent dimensions of variation, plus the intensive/extensive distinction in magnitudes, makes clear why certain analog representations admit of the Parts Principle while others do not. However, it is also clear that, in many cases, we can restrict different dimensions of variation in ways that do not amount to true mereological partitioning, but to partitioning in ways that are part-like. Thus, although it is interesting to understand why some analog representations have parts and others do not, it is not as important as understanding how different dimensions of variation can be restricted, and what smaller magnitudes within the context of a particular representational scheme amount to, whether or not they are true mereological parts.

5 . Conclusion

This paper was an attempt to make progress toward a broad, unified understanding of analog representation in all its forms. I sought to do two things. The first was to articulate a more precise account of analog representation, which required getting clearer about the kind of mapping needed between representations and representata, and distinguishing three elements of analog representational schemes: what does the representing, what is represented, and the dimension(s) along which the representation can vary. The second was to make clear why the Parts Principle applies to certain representations but not others, which required a discussion of intensive and extensive magnitudes. Along the way I suggested that whether analog representations have true mereological parts of the kind that make Parts Principle true is not as important as many have assumed, complementing the point made by ^{Clarke (2022)} .

The account offered here should be useful for those wishing to understand representation in general, as well as how representations are -or ought to be- understood in neuroscience and cognitive science. An increase in precision and clarity about any matter is probably an end in itself, but it seems particular pressing as we try to make sense of what exactly it means for some part of a natural system, such as the mind/brain, to have genuine representations. However, setting that aside, my hope is that this account adds to our understanding of both what is unique about analog representations, and the ways in which different types of analog representation are alike.¹⁴