1. Introduction
One of the most common problems of reservoir geological-petrophysical modeling workflow (Cosentino, 2001) consists in predicting petrophysical properties considering the dependency relationships with the seismic attributes. For this purpose, different methods and approaches have been used, ranging from empirical relationships (Diaz-Viera et al., 2006), regression methods, neural networks (Parra et al., 2014), (Iturraran-Viveros & Parra, 2014) to spatial stochastic models. The latter being more flexible since they better reproduce the statistical and spatial behavior of petrophysical properties(Pyrcz & Deutsch, 2014).
In the last decade, various spatial stochastic simulation methods, also known as geostatistical simulation methods, have been developed. Among the most used are: Monte Carlo simulation (Bosch et al., 2007), (Oh & Kwon, 2001) and (Grana, 2014), sequential indicator simulation (Caers et al., 2000), direct simulation (Azevedo & Soares, 2017) or sequential Gaussian simulation whose methods are widely developed in the works of (Chilès & Delfiner, 1999), (Dubrule et al., 2003), (Bortoli et al., 1993) and (Pyrcz & Deutsch, 2014).
The disadvantage of most of these methods is that they assume that the data follow Gaussian distributions and that the dependency relationships between them are linear, which makes their application to real problems very limited. In the best case, it is forced to be applied by data transformation, which produces biased results when they are back transformed.
The copula-based spatial stochastic co-simulation method was proposed by (Diaz-Viera et al., 2017) as an alternative to the aforementioned simulation methods. This method can be basically divided into two steps. Firstly, a dependence model between the primary and secondary variables is established by estimating and modeling the joint cumulative probability distribution function (CPDF) using a copula. The CPDF model is used in conjunction with a variogram (spatial correlation) model to simulate the primary variable using the second one as a conditioning variable. This last step can be done in a global optimization framework using one method, such as simulated annealing, but other methods, such as genetic algorithms, can also be applied.
Recently, the copula-based simulation method was successfully applied for the prediction of petrophysical properties using seismic attributes as a secondary variable in (Le, 2021), (Le et al., 2020), (M. Díaz-Viera et al., 2018), (Vázquez, 2018). But in these works, the method was implemented using a non-parametric approach with Bernstein copulas. The non-parametric approach has the disadvantage that it requires a high computational cost, especially when calculating the joint probability distribution function estimated with the Bernstein copula.
In this work it is proposed to use a parametric copula model, through the implementation of Archimedean copula family. This approach is expected to reduce the computational cost. The paper aim is to compare the parametric, semi-parametric and non-parametric approaches in terms of precision and performance. The comparative study is carried out through the application to two case studies in a marine reservoir in the Gulf of Mexico, where the total porosity and the density are simulated by means of the acoustic impedance and the P-wave velocity as secondary variables, respectively.
The paper has the following structure. First, the copula-based spatial stochastic co-simulation method is briefly described, distinguishing between non-parametric, semi-para- metric and parametric approaches. In particular, the members of Archimedean copula family are defined. An outline of the method application workflow is provided. Subsequently, the validation of the method is carried out by applying it to a previously published case study and the three approaches are compared. Finally, the parametric approach is applied to a new case study and the conclusions are given. In appendices, the definition of copula and its basic properties, as well as the Bernstein copula simulation method description are shown.
2. Copula-based spatial stochastic co-simulation method
Copula-based spatial stochastic co-simulation had its origins in the works of (Diaz-Viera & Casar-González, 2005), (Erdely et al., 2012) and (Hernandez-Maldonado et al., 2014). The method has the advantages of not requiring linear dependence or a specific type of distribution and has been successfully applied to simulate petrophysical properties using seismic attributes as a secondary variable. The method has been implemented mainly by a non-parametric approach using Bernstein copulas, where the copula is estimated using the empirical copula and the variables are interpolated using Bernstein polynomial function (Appendix 10.2).
However, there are two more approaches that have not been sufficiently explored and used in the dependency model estimation: semi-parametric and parametric approaches. The semi-parametric approach estimates margins non-parametrically using empirical distribution functions and parametric copula is estimated (Jaworski et al., 2010) or the margins are estimated using parametric functions and the copula is estimated non-parametrically. The parametric approach uses different parametric distribution functions that are selected and best fit the petrophysical property or seismic attribute and then couple them within the parametric copula.
The difference between the non-parametric, parametric and semi-parametric approaches lies in the estimation procedure. In the non-parametric approach, the behavior of the joint sampling distribution function is adapted by means of a polynomial approximation, reducing the estimation variance.
In the parametric approach, the data samples are fitted to copula models and parametric probability distribution functions. While the semi-parametric approach is a combination of the two previous approaches, and therefore, there are two options: parametric copulas with non-parametric marginals, or non-parametric copulas with parametric marginals. Therefore, if the joint distribution function that allows relating two or more petrophysical properties and seismic attributes in terms of their dependence is generated, it is possible to obtain more consistent simulations with their data sample statistics without having to assume a specific distribution or dependency. In the following subsections the parametric joint distribution functions are analyzed, especially the Archimedean copula family.
2.1 Parametric copula approach
The parametric copulas are a classification of copula whose advantage is to use the parameters of the joint function to control the dependence. There are three great parametric copula families: elliptical, Archimedean and extreme values (Joe, 2014).
The elliptical copulas are recommended when the dependence model is derivated from elliptical distributions and the symmetry should be elliptical respect to the diagonal (Shemyakin & Kniazev, 2017). Gaussian and t-copula are examples of elliptical copulas.
The extreme value copulas are based on random vectors distributed according to multivariate extreme value distributions. Galambos, Hüstle-Reis and Tawn are examples of extreme values copulas (Hofert et al., 2019).
Archimedean copulas are the most used copulas because they are easier for implementation, they just need one parameter θ to control the dependence and the differentiation and integration to obtain the generator and inverse is simple (Shemyakin & Kniazev, 2017). Frank, Gumbel and Clayton are examples of Archimedean copulas.
2.1.1 Archimedean copulas
After describing the basic properties of copulas (Appendix 10.1), it is necessary to study a class of copulas that will be useful for the development of Copula-based spatial stochastic co-simulation: Archimedean copulas. These copulas are very useful alternatives because they are easy to build and there is a wide variety of families of copulas with interesting properties (Nelsen, 2006).
The (Eq. 1) is the Archimedean copula. The φ function is called copula generator. Consider that if φ(0)=∞ then φ is strictly generator, in that case φ[-1] =φ-1 and C(u,v)=φ[-1] (φ(u)+φ(v)) and is said to be strictly an Archimedean copula. Another important property is the Archimedean density copula (Eq. 2), this can be expressed through the generator and its derivatives as (Shemyakin & Kniazev, 2017):
2.1.1.1 Clayton copula
This family of copulas has been used when the dependence of the tails is strong on the left and weak on the right. Generally, Clayton copula does not accept negative dependencies, the copula parameter θ is restricted into the region (0,∞), if the value of θ is zero, then the marginals become independent (Trivedi & Zimmer, 2007). Some members of Clayton copula can be implemented in models with negative dependencies; however, its use is not suggested under those conditions because the copula is not strict and it can violate the region restriction; reflecting the shape of the countermonotocity copula as the value of θ approaches -1, which itself is not an Archimedean copula. It cannot properly capture the negative dependency nor estimate the value of the parameter θ special conditions are needed to guarantee that the copula is strict (Cooray, 2018). The Clayton copula that can be evaluated in negative dependencies is defined as:
Whose generator is:
2.1.1.2 Frank copula
This family of copulas is well known because it can be used in models with positive and negative dependencies between their marginals, it is a symmetric copula on both tails and includes both Frechet limits throughout the region (-∞,∞). The disadvantage of Frank's copula is that the dependency tends to be weak in the tails and strong in the central part of the marginals; therefore, it is recommended to use this type of copula if the dependency model exhibits tails with low dependency (Trivedi & Zimmer, 2007). The Frank copula is defined as:
Whose generator is:
2.1.1.3 Gumbel-Hougaard copula
This family of copulas, like Clayton's copula, does not allow negative dependencies. The parameter θ is restricted to the interval [1,∞), if the value is 1 the copula is considered independent, if the value of θ is ∞ it is a countermonotocity copula or upper Frechet limit. Gumbel copula exhibits strong dependence on the tails located on the right and weak on left tails, therefore, it is recommended when the highest values of the sample have strong dependence, while the low values have less dependency (Trivedi & Zimmer, 2007). The Gumbel-Hougaard copula is defined as:
Whose generator is:
Joe copula
This copula family is based on Sibuya distribution LT (Joe, 2014). It only works with positive dependence and the goodness of fit is reasonably well when it is applied to small samples with moderate dependence (Hofert et al., 2019). The Joe copula is:
And the generator is:
3. Method application workflow
The workflow follows the next steps:
1. Exploratory data analysis: this step studies the variable using statistical properties, histograms and scatter plot.
2. Variographic analysis: this step consists in estimating and modeling a spatial correlation function, as the variogram, from a random function sample (M. A. Díaz-Viera, 2002).
3. Marginal estimation and model fitting: for this step the variable is fitting using parametric probability functions, the best option is selected considering the result of log-likelihood, Akaike information criteria (AIC) and Bayesian information criteria (BIC). In case of (AIC) and (BIC) criteria, the parametric function with the lowest value will be the best fit, while the log-likelihood with the highest criterion value is the best fit. However, it is advisable to use graphical tools to assess whether the fit is adequate, therefore, the fit criteria must be confirmed using the histogram, the cumulative histogram and the cumulative distribution function.
4. Parametric copula estimation and model fitting: This step uses the results obtained in step 3 and the bivariate samples to estimate and select the best Archimedean copula model. The estimation is developed using maximum likelihood (MLE), Kendall inversion τ (ITau) and Spearman inversion ρ (IRho) (Hofert et al., 2019).
5. Well-log simulation uses the joint probability distribution function using simulated annealing.
6. Compare the statistics and the spatial distribution between the variables (step 1) and the simulated variables obtained in step 5.
This algorithm is implemented using the RGEOSTAD tools (M. A. Díaz-Viera et al., 2021) and GSLIB (Deutsch & Journel, 1998).
4. Method validation
To implement the stochastic simulation using parametric, semi-parametric and non-parametric copulas, the Lakach-1 geophysical well logs are taken. This well crosses the Miocene turbiditic system. This system is important due to unassociated fields discovered in this unit; the unit is divided into three sections: Lower Miocene, Middle Miocene and Upper Miocene. The age of interest of this implementation is the Lower Miocene, in this zone the flow goes from southwest to northeast with some dominant channel systems. The rocks are medium-grained sandstones; evidence of volcanic material, feldspars, quartz and some metamorphic fragments were also found. The rock is poorly consolidated and mineralogically immature; the porosity ranges from 12 to 28% (Arreguin-Lopez et al., 2011). The interval to be evaluated is from 3035 to 3404.5 meters with a sampling interval of 0.1 meters.
4.1 Exploratory data analysis
Analyzing the geophysical well logs, the best option is the bivariate case (Ip, ϕ t ). The Figure 1 shows the well log plots.
The statistics are in Table 1, both well-logs have 3696 samples. The total porosity well-log (ϕ t ) has difference between the mean and the median is -0.0075, which is very low. Regarding the box plot (Figure 2, green histogram), most of the outliers are to the left of the graph. Meanwhile the impedance acoustic well log (Ip), the difference between the mean and the median is 158.7265, it indicates that it has positive skewness, which is possibly caused by the large number of outliers located to the right of the graph (Figure 2, blue histogram).
Table 1 Basic statistics of total porosity (ϕ t ) and acoustic impedance (Ip).
| Statistics | ϕ t | Ip |
|---|---|---|
| Samples | 3696 | 3696 |
| Minimum | 0.0620 | 5086.0072 |
| 1st quartile | 0.2147 | 6157.0051 |
| Median | 0.2295 | 6809.5573 |
| Mean | 0.2219 | 6968.2838 |
| 3rd quartile | 0.2414 | 7321.6169 |
| Maximum | 0.2939 | 11661.4642 |
| Range | 0.2319 | 6575.4569 |
| Interquartile range | 0.0267 | 1164.6118 |
| Variance | 0.0011 | 1310302.94 |
| Standard deviation | 0.0337 | 1144.6846 |
| Skewness | -1.8109 | 1.5616 |
| Kurtosis | 6.9969 | 5.7657 |
The dependency measures and the scatter plot of (Ip, ϕ t ) is in Figure 2, this shows good dependence. The Spearman measure is -0.7107, Kendall -0.5335 and Pearson -0.8563
4.2 Variographic analysis
In this step the variogram of ϕt is estimated using three models: exponential, Gaussian, and spherical. The best model selected is spherical with sill 0.0011, range 16 meters and nugget 0 (Figure 3). This model will be used to obtain the simulations using the simulated annealing method.
4.2 Parametric modeling of the marginal CDF
The (lp, ϕ t ) samples are fitted in parametric probability distribution function that allows to represent it. The Akaike information criteria (AIC), Bayesian information criteria (BIC) and log-likelihood are used to select the best option.
4.2.1 Total porosity CDF modeling
For this variable, the gamma, beta, normal, logistic, lognormal and Weibull functions were tested. The goodness of fit results for ϕ t is in Table 2 which shows the best option is Weibull function, followed by the normal function. As can see in the Figure 4, the functions cannot cover the entire histogram, only a large part of the central area, the lower values located to the left of the histogram are omitted Figure 4(A). This is confirmed in the cumulative histogram Figure 4(B), so it is possible that the results obtained in the simulation give greater importance to the largest values and not so much to the minimum values reported during the univariate analysis.
Table 2 Goodness of fit results for ϕ t
| Function | Parameter | Error | Parameter | Error | Likelihood | AIC | BIC |
|---|---|---|---|---|---|---|---|
| Weibull | α = 5.164 | 0.129 | λ = 0.220 | 0.0010 | 1791.958 | -3579.91 | -3569.90 |
| Normal | μ = 0.205 | 0.001 | σ = 0.040 | 0.0010 | 1747.720 | -3491.45 | -3481.43 |
| Logistics | μ = 0.210 | 0.001 | β = 0.028 | 0.0002 | 1735.720 | -3467.45 | -3457.44 |
| Beta | α = 11.662 | 0.489 | β = 45.080 | 1.9240 | 1685.870 | -3367.75 | -3357.74 |
| Gamma | k = 13.994 | 0.588 | β = 67.980 | 2.9130 | 1660.400 | -3316.80 | -3306.79 |
| Lognormal | Logμ=-1.610 | 0.008 | Logσ=0.280 | 0.0060 | 1598.540 | -3193.09 | -3183.08 |
4.3.2 Acoustic impedance CDF modeling
This estimation uses the following functions: gamma, normal, logistic, lognormal and Weibull, the goodness of fit results for Ip is in Table 3, the best function for Ip is lognormal, gamma function is very close to lognormal and maybe that function could be a good option, however, the lognormal function is taken.
Table 3 Goodness of fit results for Ip
| Function | Parameter | Error | Parameter | Error | Likelihood | AIC | BIC |
|---|---|---|---|---|---|---|---|
| Lognormal | Logμ=8.905 | 0.005 | Logσ=0.190 | 0.004 | -9562.235 | 19128.47 | 19138.48 |
| Gamma | k=26.558 | 0.411 | β=0.003 | 5.03e-5 | -9586.137 | 19176.27 | 19186.28 |
| Normal | μ=7513.696 | 45.850 | σ=1521.670 | 32.406 | -9647.394 | 19298.79 | 19308.80 |
| Logistics | μ=7317.655 | 45.170 | β=858.563 | 21.770 | -9653.742 | 19311.48 | 19321.50 |
| Weibull | α=4.963 | 0.108 | λ=8153.500 | 52.592 | -9710.083 | 19424.17 | 19434.18 |
As ϕ t variable, all functions fail to cover the entire histogram Figure 5(A) . Notice that the highest values are not covered. If the cumulative histogram in Figure 5(B) is examined, the interval 6000 to 7000 has good approximation to empirical function.
4.4 Copula parametric modeling
After selecting the best-fit marginal probability functions, the best-fit parametric copula is sought. Considering the dependence model has negative dependencies, it is necessary to omit the Gumbel-Hougaard copula because it is not valid on negative dependencies, Clayton copula can be calculated in negative dependencies only if the parameter estimation method is semi-parametric, for this reason the Kendall in- version τ (ITau) and Spearman inversion ρ (IRho) is used. To select the best joint distribution function, the error or standard deviation and the graphs in the Figure 6 are used. Examining the information in Table 4, the best option is Clayton copula (Figure 6(A) ). However, using this function could omit the values that are outside its coverage area, therefore the Frank's copula with the parameter estimated by maximum likelihood method (MLE) is used (Figure 6(B)).
Table 4 Fitted values for parameter θ
| Copula | Method | Parameter θ | Error |
|---|---|---|---|
| Clayton | ITau | -0.86 | 0.006 |
| Clayton | IRho | -0.92 | 0.006 |
| Frank | ITau | -15.22 | 0.030 |
| Frank | MLE | -15.04 | 0.443 |
| Frank | IRho | -14.03 | 0.664 |
4.5 Conditional joint simulation of total porosity with acoustic impedance.
After selecting the best parameters for the joint probability distribution function, a considerable number of pairs (Ip,ϕ t ) are simulated, it is proposed to simulate 40,000 observations based on the best estimate selected. The simulation samples under the parametric approach are very fast, less than a second. Considering the information in comparative Table 5, the case of ϕ t simulated and ϕ t variable has difference in the minimum values of 0.01 and maximum 0.007; in the case of mean and median, their differences are even lower. Therefore, it can be considered that the probability distribution function is representative. With the case of Ip, the difference in the minimum and maximum values have considerable differences, however, the mean and median values are very close to each other.
Table 5 Comparative between (Ip, ϕ t ) data sample and simulated using parametric copula approach.
| Statistics | ϕ t | ϕ t simulated | Ip | Ip simulated |
|---|---|---|---|---|
| Samples | 3696 | 40000 | 3696 | 40000 |
| Minimum | 0.0620 | 0.0316 | 5086.0072 | 3018.2752 |
| 1st quartile | 0.2147 | 0.1767 | 6157.0051 | 6492.1272 |
| Median | 0.2295 | 0.2089 | 6809.5573 | 7376.3306 |
| Mean | 0.2219 | 0.2065 | 6968.2838 | 7511.1841 |
| 3rd quartile | 0.2414 | 0.2388 | 7321.6169 | 8377.4856 |
| Maximum | 0.2939 | 0.3548 | 11661.4642 | 15836.6388 |
| Range | 0.2319 | 0.3233 | 6575.4569 | 12818.3636 |
| Interquartile range | 0.0267 | 0.0620 | 1164.6118 | 1885.3584 |
| Variance | 0.0011 | 0.0020 | 1310302.9400 | 2099141.1700 |
| STD | 0.0337 | 0.0455 | 1144.6846 | 1448.8413 |
| Skewness | -1.8109 | -0.2597 | 1.5616 | 0.6097 |
| Kurtosis | 6.9969 | 2.9036 | 5.7657 | 3.7259 |
In comparison, the dependency measures obtained from the simulated samples appear to be quasi linear, however this may be due to the large number of samples. Regarding the comparison in the scatter plots (Figure 7), it is noted that the joint probability distribution function fails to adequately sample the area located in the interval Ip (10000,12000) ϕ t (0.05,0.15). Sampling is abundant in the central part of the data sample (red dots), which is to be expected given the properties of Frank's copula (black dots).
4.6 Total porosity spatial simulation
The total porosity ϕ t is simulated using simulated annealing method, the GSLIB package (Deutsch & Journel, 1998) was used for the implementation. The variogram estimated for ϕ t (Figure 3) is used as objective function and considered 100 realizations. The results are shown in the comparative Table 6. The minimum, maximum, mean and median values have low differences, not greater than 0.01.
Table 6 Statistics obtained from ϕ t data sample, 100 realizations, best realization and their differences using parametric approach.
| Statistics | ϕ t data sample | ϕ t 100 realizations | Difference 100 realizations | ϕ t best realization | Difference best realization |
|---|---|---|---|---|---|
| Samples | 3696 | 369600 | 3696 | ||
| Minimum | 0.0620 | 0.0541 | 0.0079 | 0.0707 | -0.0087 |
| 1st quartile | 0.2147 | 0.2071 | 0.0076 | 0.2071 | 0.0075 |
| Median | 0.2295 | 0.2284 | 0.0011 | 0.2284 | 0.0010 |
| Mean | 0.2220 | 0.2244 | -0.0020 | 0.2244 | -0.0024 |
| 3rd quartile | 0.2414 | 0.2489 | -0.0070 | 0.2487 | -0.0072 |
| Maximum | 0.2939 | 0.3338 | -0.0400 | 0.3102 | -0.0162 |
| Range | 0.2319 | 0.2798 | -0.0480 | 0.2394 | -0.0075 |
| Interquartile range | 0.0267 | 0.0418 | -0.0150 | 0.0416 | -0.0148 |
| Variance | 0.0011 | 0.0014 | -0.0003 | 0.0014 | -0.0002 |
| STD | 0.0338 | 0.0375 | -0.0040 | 0.0375 | -0.0037 |
| Skewness | -1.8110 | -0.8640 | -0.9470 | -0.8750 | -0.9364 |
| Kurtosis | 6.9970 | 4.2437 | 2.7533 | 4.2437 | 2.7532 |
Superimposing all realizations (Figure 8(A)) dispersion in the interval 3200 to 3330 meters is noted.
5. Comparison between parametric, non-parametric and semi-parametric based copula simulations.
5.1 Non-parametric copula simulation.
The comparison with the non-parametric approach is made using a Bernstein copula for the estimation of the joint probability distribution function. The same data set (Ip, ϕ t ) is used for its implementation. As in the parametric case, 40,000 samples using the Bernstein joint distribution function are simulated (Figure 11).
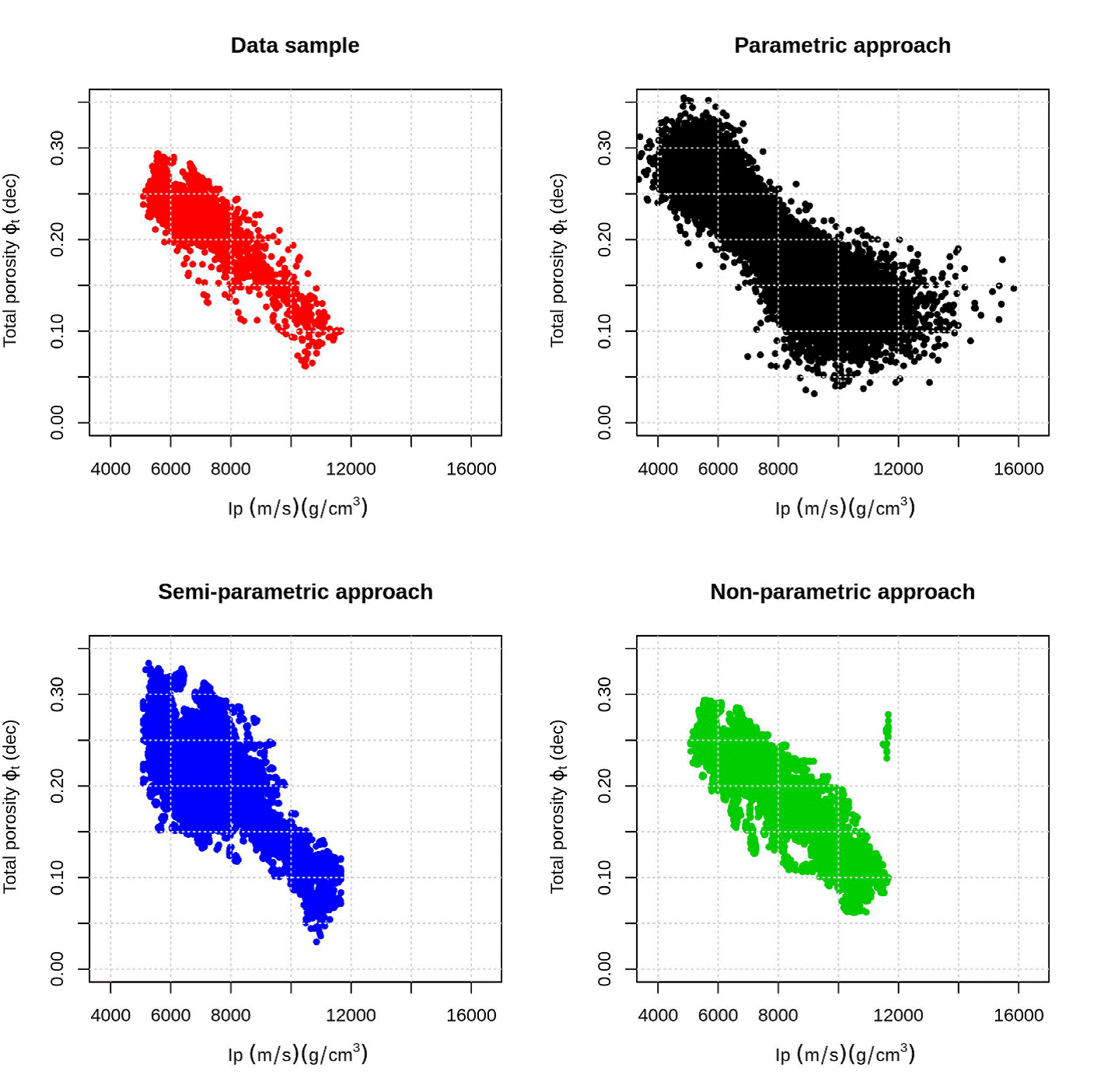
Figure 11 (Ip, ϕ t ) data samples (red dots), (Ip, ϕ t ) simulated using parametric copula (black dots), (Ip, ϕ t ) simulated using Semiparametric copula (blue dots) and (Ip, ϕ t ) simulated using non-parametric copula (green dots).
Each step takes around 10 hours, which compared to the time of parametric copula estimate, is too much. However, the statistics obtained from this estimate are very close to data samples (Table 7), this is confirmed in the Figure 11, the samples simulated using Bernstein copula (green dots) are close to data sample.
Table 7 Comparative between (Ip, ϕ t ) data samples and data simulated using non-parametric approach.
| Statistics | ϕ t | ϕ t simulated | Ip | Ip simulated |
|---|---|---|---|---|
| Samples | 3696 | 40000 | 3696 | 40000 |
| Minimum | 0.0620 | 0.0620 | 5086.0072 | 5086.0072 |
| 1st quartile | 0.2147 | 0.2147 | 6157.0051 | 6157.0052 |
| Median | 0.2295 | 0.2295 | 6809.5573 | 6809.5574 |
| Mean | 0.2219 | 0.2220 | 6968.2838 | 6968.2839 |
| 3rd quartile | 0.2414 | 0.2415 | 7321.6169 | 7321.6170 |
| Maximum | 0.2939 | 0.2938 | 11661.4642 | 11661.4642 |
| Range | 0.2319 | 0.2318 | 6575.4569 | 6575.4570 |
| Interquartile range | 0.0267 | 0.0268 | 1164.6118 | 1164.6118 |
| Variance | 0.0011 | 0.0011 | 1310302.9400 | 1309980.6378 |
| Standard deviation | 0.0337 | 0.0338 | 1144.6846 | 1144.5439 |
| Skewness | -1.8109 | -1.8212 | 1.5616 | 1.5617 |
| Kurtosis | 6.9969 | 7.0257 | 5.7657 | 5.7657 |
100 simulations using the samples obtained from Bernstein copula are made. As shown, the spatial distributions (Figure 9) obtained using the Bernstein copula are even closer to the data sample distribution. However, the computational cost is high, the simulation of 40,000 samples can take hours.
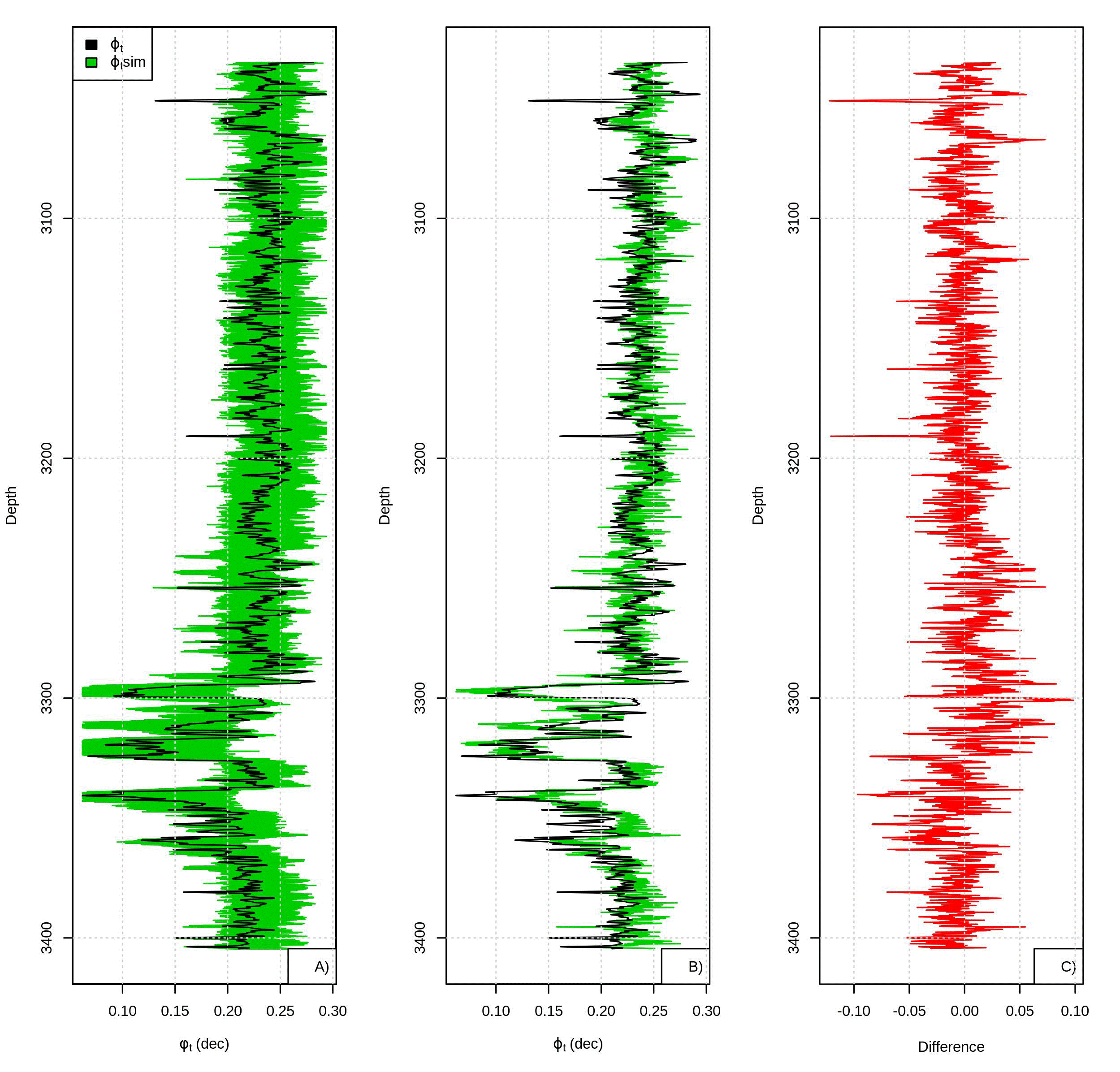
Figure 9 Realizations (green) superimposing over ϕ t (black), B) Best realization obtained and C) difference between well-log ϕ t and best simulated ϕ t .
Table 8 Statistics obtained from ϕ t data sample, 100 realizations, best realization and their differences using non-parametric approach.
| Statistics | ϕ t data sample | ϕ t 100 realizations | Difference 100 realizations | ϕ t best realization | Difference best realization |
|---|---|---|---|---|---|
| Samples | 3696 | 369600 | 3696 | ||
| Minimum | 0.0620 | 0.0620 | 0 | 0.0622 | -0.0002 |
| 1st quartile | 0.2147 | 0.2154 | -0.0006 | 0.2154 | -0.0006 |
| Median | 0.2295 | 0.2295 | 0 | 0.2294 | 0.0001 |
| Mean | 0.2220 | 0.2220 | 0 | 0.2220 | 0 |
| 3rd quartile | 0.2414 | 0.2413 | 0.0001 | 0.2412 | 0.0002 |
| Maximum | 0.2939 | 0.2938 | 0.0001 | 0.2868 | 0.0071 |
| Range | 0.2319 | 0.2318 | 0.0001 | 0.2246 | 0.0072 |
| Interquartile range | 0.0267 | 0.0259 | 0.0008 | 0.0258 | 0.0009 |
| Variance | 0.0011 | 0.0011 | 0 | 0.0011 | 0 |
| STD | 0.0338 | 0.0330 | 0.0008 | 0.033 | 0.0008 |
| Skewness | -1.8111 | -1.9460 | 0.1349 | -1.97 | 0.1590 |
| Kurtosis | 6.9970 | 7.4361 | -0.4391 | 7.5698 | -0.5728 |
5.2 Semi-parametric copula simulation.
This is formed using Bernstein copula and parametric marginals, the marginals are Lognormal (Ip) and Weibull (ϕ t ). The statistics obtained are close for Ip; ϕ t has differences, especially in minimum and maximum (Table 9). Comparing the scatter plot (Figure 11) the samples obtained with semi-parametric joint distribution function are between Frank copula and Bernstein copula. The computational cost is 10% less than the Bernstein copula, but the statistics are not the same.
Table 9 Comparative between (Ip, ϕ t ) data sample and data simulated using semi-parametric approach.
| Statistics | ϕ t | ϕ t simulated | Ip | Ip simulated |
|---|---|---|---|---|
| Samples | 3696 | 40000 | 3696 | 40000 |
| Minimum | 0.0620 | 0.0298 | 5086.0072 | 5086.0072 |
| 1st quartile | 0.2147 | 0.1967 | 6157.0051 | 6157.0052 |
| Median | 0.2295 | 0.2217 | 6809.5573 | 6809.5574 |
| Mean | 0.2219 | 0.2183 | 6968.2838 | 6968.2839 |
| 3rd quartile | 0.2414 | 0.2459 | 7321.6169 | 7321.6170 |
| Maximum | 0.2939 | 0.3340 | 11661.4642 | 11661.4642 |
| Range | 0.2319 | 0.3042 | 6575.4569 | 6575.4570 |
| Interquartile range | 0.0267 | 0.0492 | 1164.6118 | 1164.6118 |
| Variance | 0.0011 | 0.0017 | 1310302.9400 | 1309983.8600 |
| STD | 0.0337 | 0.0411 | 1144.6846 | 1144.5453 |
| Skewness | -1.8109 | -0.6140 | 1.5616 | 1.5617 |
| Kurtosis | 6.9969 | 3.8246 | 5.7657 | 5.7657 |
Comparing the 100 ϕ t simulations (Figure 10), the realizations are centered, this does not happen with the realizations obtained using Frank copula samples, but have more dispersion than the realizations obtained using the Bernstein copula samples, the statistics between data sample and data simulation are very close (Table 10).
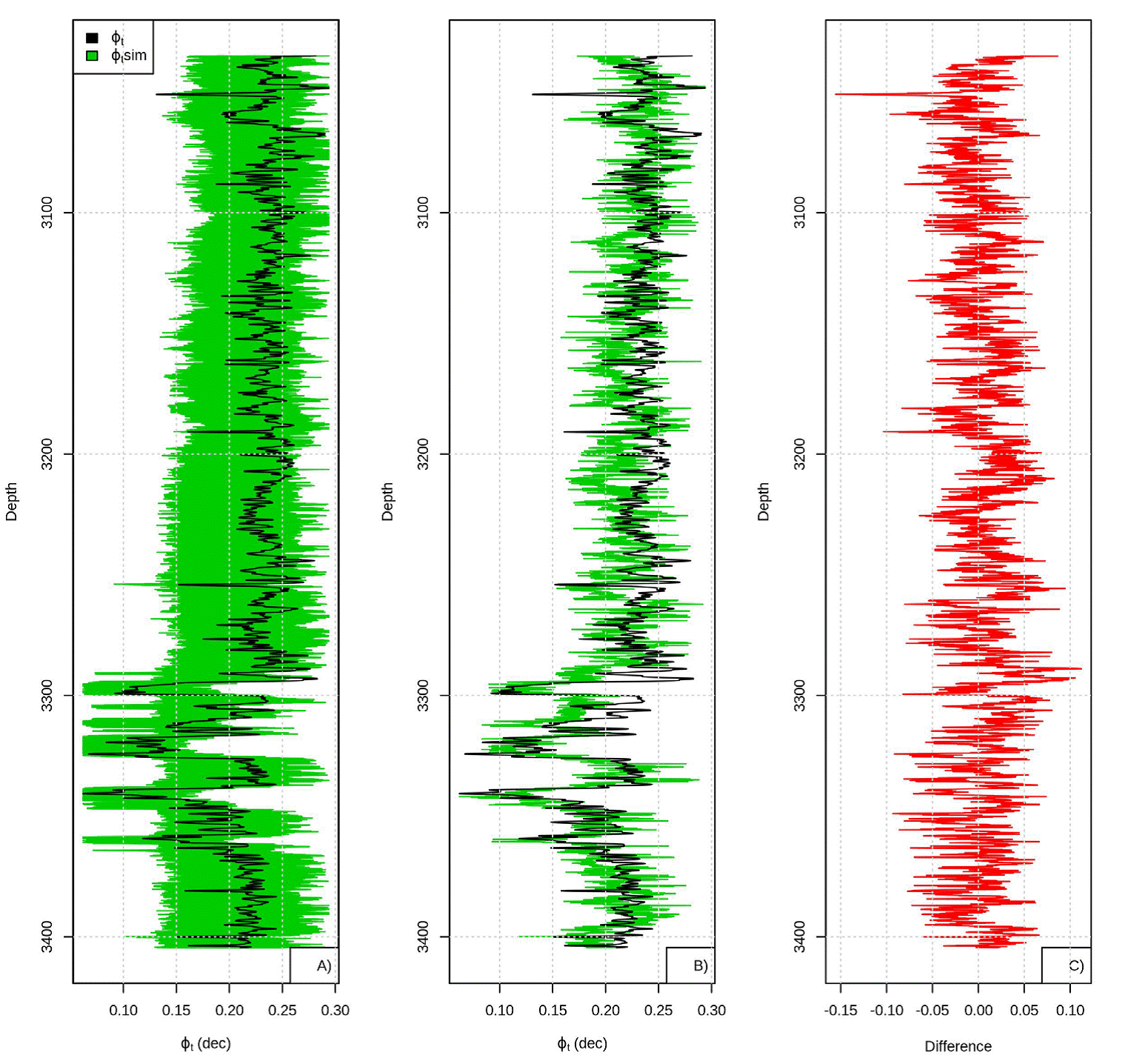
Figure 10 Realizations (green) superimposing over ϕ t (black), B) Best realization obtained and C) difference between well-log ϕ t and best simulated ϕ t .
Table 10 Statistics obtained from ϕ t data sample, 100 realizations, best realization and their differences using semi-parametric approach.
| Statistics | ϕ t data sample | ϕ t 100 realizations | Difference 100 realizations | ϕ t best realization | Difference best realization |
|---|---|---|---|---|---|
| Samples | 3696 | 369600 | 3696 | 3696 | |
| Minimum | 0.0620 | 0.0608 | 0.0012 | 0.0637 | -0.0017 |
| 1st quartile | 0.2147 | 0.1979 | 0.0168 | 0.1978 | 0.0169 |
| Median | 0.2295 | 0.2216 | 0.0079 | 0.2215 | 0.0080 |
| Mean | 0.222 | 0.2182 | 0.0038 | 0.2181 | 0.0039 |
| 3rd quartile | 0.2414 | 0.2453 | -0.0039 | 0.2456 | -0.0042 |
| Maximum | 0.2939 | 0.3226 | -0.0287 | 0.3054 | -0.0115 |
| Range | 0.2319 | 0.2617 | -0.0298 | 0.2418 | -0.0099 |
| Interquartile range | 0.0267 | 0.0474 | -0.0207 | 0.0479 | -0.0212 |
| Variance | 0.0011 | 0.0015 | -0.0004 | 0.0015 | -0.0004 |
| STD | 0.0338 | 0.0383 | -0.0045 | 0.0382 | -0.0044 |
| Skewness | -1.8110 | -0.7330 | -1.0780 | -0.751 | -1.0600 |
| Kurtosis | 6.9970 | 3.7493 | 3.2477 | 3.7789 | 3.2181 |
As shown in Table 11, the non-parametric approach almost perfectly reproduces the existing dependency relationship in the data sample, while the parametric and semi-parametric approaches either overestimate or underestimate it, respectively.
Table 11 Comparison of (Ip, ϕ t ) dependency measures among the parametric, semi-parametric and non-parametric approaches with respect to the data samples.
| Pearson | Spearman | Kendall | |
|---|---|---|---|
| Data sample | -0.8563 | -0.7107 | -0.5335 |
| Parametric approach | -0.8886 | -0.9306 | -0.7649 |
| Semiparametric approach | -0.6780 | -0.5074 | -0.3671 |
| Non-parametric approach | -0.8481 | -0.7073 | -0.5303 |
6. Application to case study: density vs. P- wave velocity
This example uses (Vp,ρ) well logs. The statistics (Table 15) and the histograms of Vp (Figure 12, blue histogram) and ρ (Figure 12, green histogram) show high asymmetry although the difference between median and median is low in both variables. This case has positive dependence (Figure 12), but the dependence is less compared with the (Ip,ϕ t ) case. So, the use of Frank, Gumbel, Clayton and Joe copula is allowed.
Table 15 Comparative between (Vp, ρ) data samples and simulated using Joe copula.
| Statistics | Vp | Vp simulated | ρ | ρ simulated |
|---|---|---|---|---|
| Samples | 3696 | 40000 | 3696 | 40000 |
| Minimum | 2448.0983 | 1619.7990 | 2.0085 | 1.8630 |
| 1st quartile | 2785.1214 | 2843.1401 | 2.1835 | 2.1873 |
| Median | 3011.4426 | 3112.6668 | 2.2395 | 2.2568 |
| Mean | 3088.0889 | 3129.2969 | 2.2494 | 2.2590 |
| 3rd quartile | 3273.1712 | 3398.5189 | 2.3062 | 2.3276 |
| Maximum | 4608.5457 | 5038.7143 | 2.6031 | 2.7328 |
| Range | 2160.4473 | 3418.9152 | 0.5946 | 0.8697 |
| Interquartile range | 488.0498 | 555.3788 | 0.1227 | 0.1402 |
| Variance | 165004.4920 | 168551.6370 | 0.0087 | 0.0110 |
| Standard deviation | 406.2074 | 410.5504 | 0.0934 | 0.1050 |
| Skewness | 1.2392 | 0.2460 | 0.6631 | 0.1302 |
| Kurtosis | 4.5799 | 3.0456 | 3.5973 | 3.0462 |
The variogram model estimated for ρ (Figure 13) is spherical with sill 0.0083, range 15 meters and nugget effect 0.
The parametric estimation for ρ (Table 12) suggests the lognormal function as best option, but the cumulative distribution functions in Figure 14(B) shows all functions, except Weibull function has good fit. Gamma and normal functions have likelihood, AIC and BIC very close to lognormal.
Table 12 Goodness of fit results for ρ
| Function | Parameter | Error | Parameter | Error | Likelihood | AIC | BIC |
|---|---|---|---|---|---|---|---|
| Lognormal | Logμ =0.8130 | 0.009 | Logσ =0.04 | 0.006 | 1845.260 | -3686.52 | -3675.11 |
| Gamma | k = 455.2500 | 13.650 | β=201.60 | 6.050 | 1838.346 | -3672.69 | -3661.28 |
| Normal | μ = 2.2581 | 0.002 | σ = 0.10 | 0.001 | 1822.310 | -3640.63 | -3629.22 |
| Logistics | μ = 2.2524 | 0.002 | β = 0.06 | 0.001 | 1804.600 | -3605.21 | -3593.80 |
| Weibull | α= 20.278 | 0.303 | λ = 2.31 | 0.002 | 1568.410 | -3132.83 | -3121.42 |
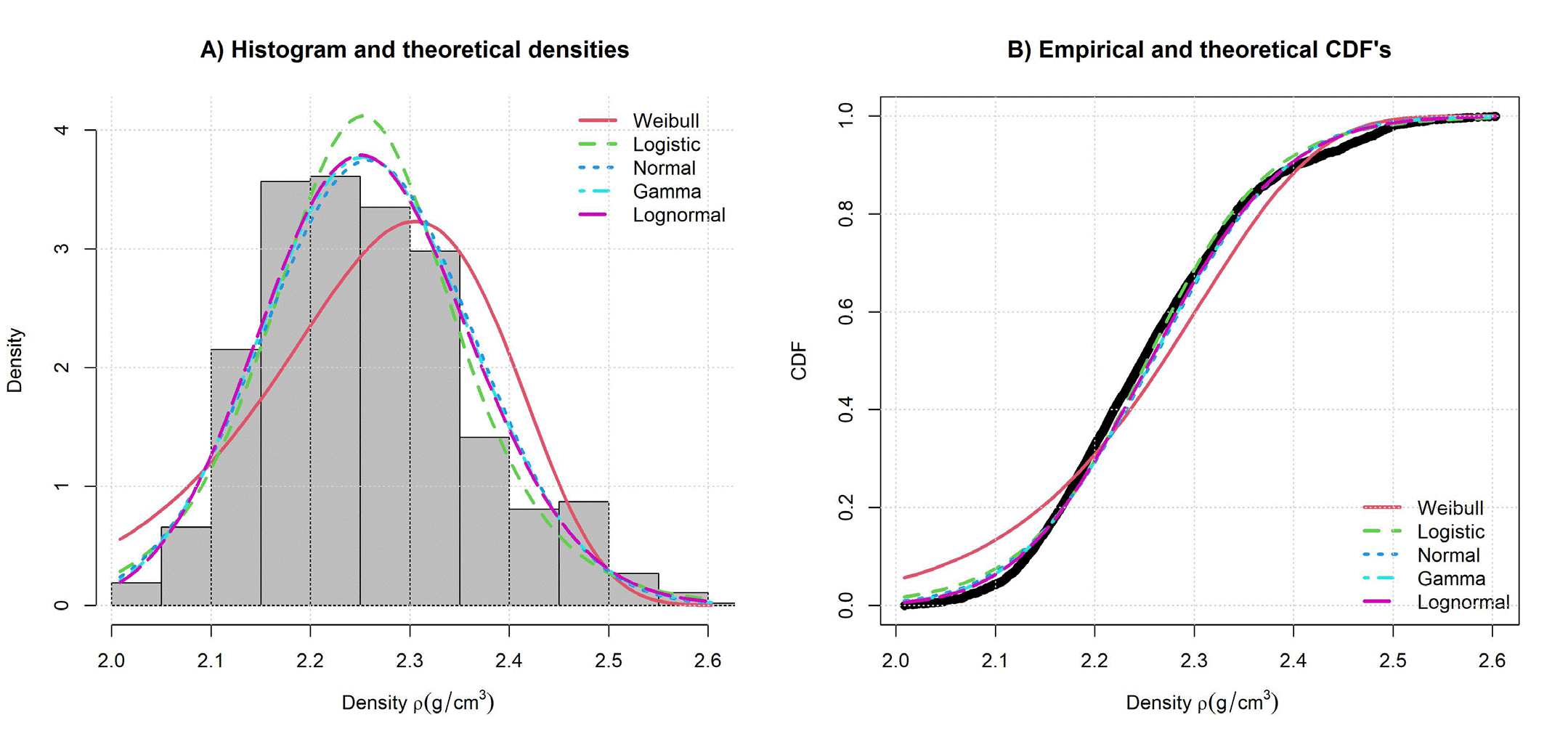
Figure 14 Histogram and theoretical densities (A) and empirical and theoretical CDF’s (B) of Goodness of fit results for ρ
Now, the Vp variable goodness of fit results in Table 13 shows gamma function as best option, Logistic and lognormal are close to gamma function results, and the graphs in Figure 15 demonstrate that gamma and lognormal functions have similar fitted.
Table 13 Goodness of fit results for Vp
| Function | Parameter | Error | Parameter | Error | Likelihood | AIC | BIC |
|---|---|---|---|---|---|---|---|
| Gamma | k = 58.244 | 1.440 | β = 0.018 | 0.0004 | -16500.00 | 33004.01 | 33015.42 |
| Logistic | μ =3069.300 | 8.140 | β = 224.63 | 4.0810 | -16523.25 | 33050.51 | 33061.92 |
| Lognormal | Logμ = 8.039 | 0.002 | Logσ =0.12 | 4.0800 | -16523.44 | 32902.89 | 32914.30 |
| Normal | μ =3128.730 | 9.117 | σ = 429.69 | 6.4470 | -16617.57 | 33239.13 | 33250.54 |
| Weibull | α= 6.628 | 0.096 | λ = 3325.87 | 11.3400 | -16903.62 | 33811.24 | 33822.65 |

Figure 15 Histogram and theoretical densities (A) and empirical and theoretical CDF’s (B) of Goodness of fit results for Vp
The fit copula results show Joe copula model as best option (Table 14). Gumbel copula could be a good option, but Joe copula can cover the pseudo-observations, especially the samples in the extremes (Figure 16).
Table 14 Fitted values for parameter θ
| Copula | Method | Parame- ter θ | Error | Loglikeli- hood |
|---|---|---|---|---|
| Joe | MLE | 2.038 | 0.044 | 550.6 |
| Gumbel | MLE | 1.643 | 0.028 | 522.6 |
| Frank | MLE | 3.671 | 0.141 | 342.4 |
| Clayton | MLE | 0.570 | 0.035 | 170.2 |
Simulating 40,000 samples from Joe copula, superimposing the results (Figure 17) the drop form of Joe copula samples is evident. The measures of dependences show Pearson values have difference of 0.02, but Spearman and Kendall measures are high. Other characteristic is the scatter of Joe copula samples, simulated samples are near to data samples. Comparing the variance and standard deviation in Table 15, the values are very close, this is not the same with the validation case, this could be an advantage of positive dependence.
The spatial distributions obtained to 100 simulations (Figure 18) show good covering except in the interval 3350- 3400, the variance in that range is high.
7. Conclusions
In the comparison between parametric, semi-parametric and non-parametric approaches of the spatial stochastic simulation method based on copulas, it is concluded that the parametric approach has a very low computational cost, since its execution lasts only a few seconds; while the semi-parametric and non-parametric approach can take up to hours. Given that the first approach involves analytic functions in the calculation, while the second approach requires the calculation of the joint probability distribution function through the numerical approximation of the copula and its marginals with Bernstein polynomials.
When comparing the numerical results, it can be verified that the parametric approach does not reproduce data statistics such as minimum, maximum, skewness and kurtosis with the same precision as the semi-parametric and non-parametric approach. The parametric approach presents a greater dispersion expressed by its variance, which means more uncertainty. This fact is due to it is practically impossible to be able to represent the underlying dependence complexity between data with a parametric model, since the data is forced to fitting an analytical model depending of a single parameter, whereas the objective is to represent the real dependence complexity existing in the data, the latter only could be done by the non-parametric approach.
This indicates that it is advisable to use the parametric approach in cases with large data samples and limited computing capabilities. This problem would be expected to occur when the method is applied in three spatial dimensions and when more than two variables are included in the multivariate joint estimation as well. However, the non-parametric approach could be applied if the appropriate computational capabilities are available and predictions with less uncertainty are required.











 nova página do texto(beta)
nova página do texto(beta)
















