1.Introduction
Nanotechnology is a promising field because of the novel properties that the materials could display at nanoscale, more specifically magnetism at nanometer scale attracts considerable attention due to fundamental and technological perspectives 1-5. For example, for high density magnetic recording one would likely be able to develop magnetic nanoparticles that combine both high saturation magnetization and large Magnetic Anisotropy Energy (MAE). The MAE determines the stability of the magnetization direction and the orientation of the magnetization with respect to the lattice structure. Also, magnetic nanoparticles offer great possibilities in biomedicene , for instance magnetic separation of labelled biological entities from its native environment using biocompatible nanoparticles, localized drug delivery reducing the side effects and the dosage, the posibility of treating cancer by induced hyperthermia dispersing magnetic nanoparticles throughout the target tissue and applying an external magnetic field, contrast enhancement agents for MRI and many more applications.
Theoretical research has been done in both infinite and finite linear chains of cobalt atoms. For freestanding infinite chains Guo and Tung 7,8 made a systematic ab initio study of the magnetic and electronic properties of all 3d, 4d and 5d transition metals for both linear and zigzag nanowires, Kim et al. 9 with the WIEN97 code investigated the change in the electronic structure and magnetic moment of transition metals of group 8-10 as their dimensionality is reduced, they predicted that all are magnetic in 1D, except Ir. For finite linear chains Weinberger et al. 10 studied the magnetic properties of cobalt chains on Pt(111) and Bruno et al. 11 studied the structure and magnetic properties of cobalt chains on a stepped Cu surface. For cobalt monoatomic chains on top of the Cu(001) and Pt(001) see 12.
Nanostructures are not only a theoretical subject, experimental research has been done in the past years, linear Aun chains with
Heisenberg model calculations with finite range exchange interaction show that in a one dimensional chain, ferromagnetism cannot be maintained at finite temperature 16. On the other hand, the inclusion of a strong magnetic anisotropy can modify this statement as was shown experimentally by Gambardella et al. 17, growing cobalt chains on a Pt(997) surface they showed evidence that in 1-D 3d metal chains can sustain both short and long range ferromagnetic order at a finite temperature. Cobalt has a strong tendency to magnetize due to their partially filled d-orbitals and exhibits magnetism in their bulk structures. For finite linear cobalt chains it is important to investigate the possibility of ferromagnetism at ground state. A lot of work has been done theoretically and experimentally but the understanding on the magnetic properties of freestanding finite linear cobalt chains and how magnetism affects their structural properties is still incomplete. At the best of our knowledge there is no such study.
In the present paper we study the magnetic properties of freestanding Con linear chains in the ground state with different length (
2.Theory and computational Method
The calculations are performed in the framework of Hohenberg-Kohn-Sham’s density functional theory21 as implemented in the Vienna ab initio simulation package (VASP)22. This computer software solves the spin-polarized Kohn-Sham (KS) equations with an augmented plane-wave basis set that use the projector augmented wave (PAW) method21,24, which is an approximate all-electron approach with frozen cores. The exchange and correlation effects are treated in the generalized-gradient approximation (GGA) by using the Perdew-Burke-Ernzerhof (PBE) functionals23. For 3d transition metals, the electronic and magnetic properties are reliably described by considering as valence electrons the 3d, 4s, and 4p states24.
The cobalt chains are placed inside a supercell which dimensions are such that the interactions between neighboring images are negligible. In practice, this criterion is satisfied when the images are separated from each other by at least 12 Å. The KS wave functions in the interstitial region are expanded in a plane wave basis set with a kinetic energy cut-off of 575 eV, this value guarantees that the total energy converges within less than 1 meV/per atom. For metallic-like systems, one often finds very rapid variations of states close to the Fermi level that may cause a poor convergence of relevant physical quantities such as the total energy, therefore, a smearing of the KS levels is introduced in order to improve numerical stability. We have used a Gaussian smearing method with a standard deviation σ between 0.001 eV and 0.0002 eV, the 𝜎 value is different for each chain to keep the entropy of the non-interacting KS gas below 10-6 eV/K-atom. For small chains,
Figure 1 represents a linear Con chain with n = 10,
3.Ab initio results
3.1.Bond lengths and Binding energy
With the optimized structure coordinates we compute the distances
TABLE I This table shows de distance between the l-atom and the (l + 1)-atom for the Con chains with 2 ≤ n ≤ 10. The distance between any nearest neighbors in a infinite linear chain is 2.15 °A .
| n= | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| d1,2 | 1.96 | 2.12 | 2.00 | 2.02 | 2.02 | 2.00 | 2.02 | 2.02 | 2.02 |
| d2.3 | 2.12 | 2.56 | 2.25 | 2.26 | 2.31 | 2.27 | 2.27 | 2.32 | |
| d3.4 | 2.00 | 2.25 | 2.10 | 2.10 | 2.14 | 2.13 | 2.09 | ||
| d4,5 | 2.02 | 2.26 | 2.10 | 2.16 | 2.20 | 2.18 | |||
| d5,6 | 2.02 | 2.31 | 2.14 | 2.20 | 2.16 | ||||
| d6,7 | 2.00 | 2.27 | 2.13 | 2.18 | |||||
| d7,8 | 2.02 | 2.27 | 2.09 | ||||||
| d8,9 | 2.02 | 2.32 | |||||||
| d9,10 | 2.02 |
We can see from Table I that for small chains a dimerization is generated, for long chains this effect almost disappears in the center but it is maintained at the ends of the chains. The dimerization effect is shown with more clarity for the chains of 4 and 10 atoms. For Co4 the distance between atom 1 and 2
where E(1) is the energy of one cobalt atom and E(n) is the Con chain energy, both energies are in ground state. Figure 2 shows Eb in function of the inverse number of atoms 1/n for the cobalt chains in the easy axis. Plotting Eb in function of 1/n allow us to represent the infinite cobalt chain binding energy at cero. We fit the data with the best straight line using the least squares method. The line equation is
3.2. Spin and orbital magnetic moments
The results of the spin moment S and orbital moment L in the easy axis for the central most symmetric atom in the cobalt chains are shown in Fig. 3. The upper graph shows the spin moment S in function of the length chain n, the dashed line at 2.23 is the spin moment S for an infinite linear chain. The single cobalt atom has the highest spin moment (2.4
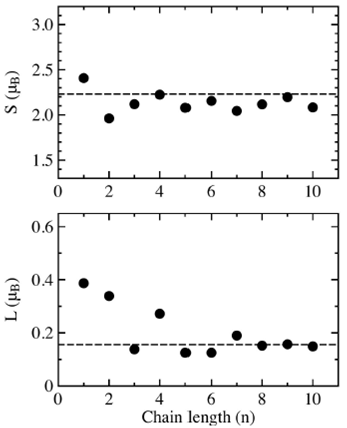
FIGURE 3 Calculated spin S and orbital moment L of the central (most symmetric) atom in Con (n=1,. . . ,10) chains for the easy axis. The dashed lines at 2.23 and 0.156 represent the S and L values for the infinite chain.
The lower graph of Fig. 3 shows the orbital moment L of the central atom in the cobalt chain in function of the length chain n, the dashed line al 0.156 is the orbital moment L for an infinite linear chain. First we notice that the single atom orbital moment L= 0.39
The spin moment S of each atom forming the chain is shown in Fig. 4. We notice that the spin moments at the end of the chains for (n=1, 2,…,10) are higher that those in the middle of the chains.. Also the distribution of the spins becomes flat as the chain grows, except for Co9 that has a small peak in the middle. The single cobalt atom has the highest spin moment S = 2.4
4. Magnetic Anisotropy
We investigated the magnetic anisotropy energy, this is a very important characteristic in magnetic materials because it gives the magnetic moments orientation in the system and determines the stability of the magnetization direction with respect to external fields. We computed the magnetic anisotropy energy of cobalt chains between X axis and Z axis and we define the MAE as the energy difference between X and Z axis, thus positive and negative values are posible. Figure 6 shows the MAE per atom in function of 1/n, in this case there is not a linear scaling, actually it is very irregular but apparently it decreases for long chains. For the Con chains with (
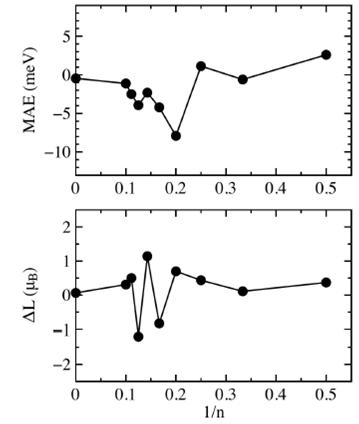
FIGURE 6 Upper graph shows the magnetic anisotropy energy per atom in function of 1=n. Lower graph shows the difference of the orbital moment ¢L between the X and Z axis.
The lower graph in Fig. 6 shows the difference of the orbital moment
5.Conclusions
We studied the ground state magnetic properties of Con linear atomic chains with











 nova página do texto(beta)
nova página do texto(beta)






