3.1.Molecular Structure

In 1985, the crystal structure of NAM has been reported by Ponnuswamy and Trotter ²⁵ and five years later, redetermined it and its calcium adduct viz., Ca(𝑁-acetyl-DL-methionine)₂. H₂O by Kim and Eriks ²⁶. Moovendaran and Natarajan reported structure and some other properties by recording X-ray, IR, UV-Vis-NIR, TGA/DTA, and photoluminescence spectra ²⁷. According to the best of our knowledge, in the literature, there are no available spectroscopic and quantum chemical calculation results for this compound and, therefore, we calculated for the molecular structure for the first time. For the compound, we have employed a 6-311++G(d,p) basis set at B3LYP and HSEH1PBE levels without symmetry constrain, to provide integrity and compared computed geometry parameters through experimental bond lengths and bond angles, which are taken from Refs. ^25,26. The atom numbering scheme for the molecule is shown in Fig. 1a) ²⁵.

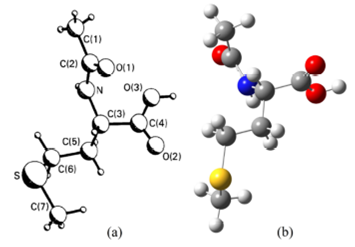
Figure 1 a) The experimental structure and b) the optimized molecular structure obtained by the B3LYP method for NAM. 

The optimized molecular geometry of the title molecule has been obtained in the gas phase at B3LYP/6-311++G(d,p) level using is shown in Fig. 1 (b). NAM contains a carboxyl group (-C4(O2)O3H), an N-acetyl group (-NHC2O1C1H₃), and a side chain (-C5H₂SC6H₃C7H₂) attached to a C3 atom (see Fig. 1). According to the available reported studies in the literature, the calculated lattice parameters are gathered in Table I, and for these analyses confirm that the crystal belongs to the monoclinic crystal system with space group P21/c with Z = 4 number of formula units in the unit cell.

Table II gives the unscaled theoretical geometry parameters and also experimental X-ray data of the title compound with the estimated standard deviations in parentheses. It is observed that calculated values of bond lengths and bond angles through both methods B3LYP and HSEH1PBE are closer to each other.

In consideration of the bond lengths, as shown in Table, most of the calculated values are higher than experimental ones but this can be explained by the differences in the solid-state and liquid or gas phases. The experimental values were performed for the solid phase, while the theoretical calculations were for the isolated molecule in the gas phase. The observed differences of bond parameters between the calculated and experimental values being most probably due to the subsistence of the crystal field along with the intermolecular interactions have connected the molecules, which occur in the crystal.

It can be observed that the C1-C2, C3-C4, C3-C5, and C5-C6 carbon-carbon bond lengths on the molecule are smaller than typical C-C single (1.54 Å) bond, and the C2-N bond lengths in the peptide group of the title compound are much shorter than the normal C-N single bond that is referred to 1.49 Å, which confirms this bond to have some characteristics of a double or conjugated bond ²⁸. The C3-N carbon-nitrogen bond length is intermediate between C-N typical single bond characteristics, as presented in related compounds previously studied ²⁹.

C-C bond lengths in the range of ∼1.509-1.546 Å are also close to the experimental bond lengths in the range of ∼1.483-1.531 Å, varying with a little difference. In the title compound, the carbon sulfur bond lengths C6-S and C7-S are 1.833 Å and 1.827 Å with B3LYP and 1.814 Å and 1.809 Å with HSEH1PBE while the reported values are in the range ∼1.764-1.796 Å^25,26. As discussed by Johnson et al., the various DFT methods predict bond lengths, which are systematically too long (30). The results of the calculated bond lengths of NAM molecule using DFT methods have provided proof of these findings. According to Table I, the computed C2-N bond length (1.379 and 1.372 Å) is a bit longer than from experimental bond lengths (1.333 and 1.330 Å).

The shortening of the bond length of C2-O1 (∼1.237 Å) and C4-O2 (∼1.206 Å) could be assigned a double bond character, whereas the corresponding values for the title compound are 1.219 Å 1.215 Å (B3LYP) and 1.204 Å, 1.201 Å (HSEH1PBE).

Computed C1-C2-N, C1-C2-O1, and N-C2-O1 bond lengths of the side chain have the same values (respectively, 117^o, 122^o, and 120 ^o) with the experimental results. About the X-ray data, the bond angle C2-N-C3 is ∼121.2^o, whereas it is computationally 128.0^o and 127.4^o with B3LYP and HSEH1PBE methods, respectively, which provide the possibility of the presence of hydrogen bond. According to literature ^25,26 only two hydrogen bonds are formed between neighboring molecules N-H⋯O2 and O3-H⋯O1.

On the other hand, the carbon-carbon-oxygen bond angles in the carboxyl group lie in the range 111.9-124.8^o, (DFT) and 113.3-122.5^o (XRD). The bond angles are C4-C3-C5=109.3^o, C4-C3-N=112.9^o, and C5-C3-N=111.1^o (DFT), and this asymmetry gives the interaction between the carboxyl group and the neighboring peptide group and side chain.

3.2.Vibrational wavenumbers

Vibrational frequency calculations for the ground spin state of the NAM were calculated with the same level of theory calculations based on the optimized geometries. The experimental IR spectra were compared with the calculated spectra (Fig. 2), and also theoretical and experimental absorption frequencies and assignments of the title compound are listed in Table III. The vibrational band assignments have been made using the GaussView molecular visualization program ³.

Figure 2 Experimental and calculated IR spectra for NAM. 

According to the literature ³¹, there are disagreements in the calculated harmonic vibrational frequencies when they are compared to the experimental fundamental vibrational frequencies, and these discrepancies can partially be attributed to two errors: the neglect of anharmonicity and the inaccurate description of the electron-electron interaction. A scaling factor is commonly used to correct the calculated value to match the experimental observable. Therefore, we used 0.96 ³² scale factors for the computed frequencies of the NAM. All the experimental results were confirmed by Moovendaran and Natarajan ²⁷.

The asymmetric stretching mode v(N-H) is located 3343 cm^-1 experimentally (3435 and 3469 cm^-1 at DFT), while the weak stretching mode v(C=O) were around 2461 cm^-1 experimentally (1740 and 1776 cm^-1 at DFT) after we applied the scale factor. The calculated results by frequency analysis indicate deviations from experimental values due to the intramolecular hydrogen bond between N and O. The bands corresponding to both out of the plane and in-plane C-H deformations are calculated in the region 1164-1287 cm^-1. The bending vibrations for γ(N-H) and β(C-N-H) groups in IR spectra are observed in the region 1618 and 1560 cm^-1, respectively, while the calculated vibration frequencies of them are ~1444 cm^-1 and 1421 cm^-1, respectively. On the other hand, the bands at 1115, 1042, and 1015 cm^-1 are assigned to the v(C-N) vibration, and the theoretically computed values are observed in the wave region 1099-961 cm^-1. The theoretically computed values of p(CH₃) vibration mode at ∼935 cm^-1 show a good agreement with the experimental value at 961 cm^-1. The IR band at 1693 cm^-1 in the experimental IR spectrum of the title compound were designated to v(C=O) symmetric stretching fundamentals of C4 and O2 atoms, and this band appeared at 1681 cm^-1 (B3LYP) and 1718 cm^-1 (HSEH1PBE) in the DFT calculations. The v(CH₂-S) stretching mode is another typical mode for NAM, and this vibration experimentally appeared at 2920 cm^-1. Theoretically, this band could be assignable to: at 2919 cm^-1 for the B3LYP method and 2936 cm^-1 for the HSEH1PBE method.

3.3.NMR studies

The structural parameters are obtained with the B3LYP and HSEH1PBE functional and 6-311++G(d,p) basis set, and they are used to predict ¹³C and ¹H NMR chemical shifts with the recommended GIAO, CSGT, and IGAIM approaches and Tetramethylsilane (TMS) is used for reference. The isotropic magnetic shielding values were used to calculate the isotropic chemical shifts (δ) with respect to TMS (δisoX=σisoTMS-σisoX). The appropriate value of the ¹H/¹³C isotropic chemical shifts for TMS (σisoTMS) was found to be 184.0807/31.9723 ppm for GIAO, 182.3844/30.7302 ppm for IGAIM, and 182.3611/30.7287 ppm for CSGT by B3LYP/6-311++G(d,p). Those obtained by HSEH1PBE level were also found to be 188.3372/31.8158ppm for GIAO, 186.7863/30.5605 ppm for IGAIM, and 186.7641/30.5590 ppm for CSGT.

The experimental and theoretical values for ¹³C and ¹H NMR chemical shifts of the title molecule are given in Table IV. The correlation values between the experimental and calculated chemical shifts in Table IV shows that all computations are in good agreement with the experimental data except the proton of the amino group in ¹H NMR. The chemical shifts of the hydrogen atoms of the CH3 groups are 2.040 ppm (C1), 1.850 ppm (C7), and the hydrogen atom of the CH₂ groups are 1.93 (C5), 1.82 ppm (C5), 2.48 ppm (C6) experimentally. In our present investigation, the chemical shifts of hydrogen atoms in the CH₃ groups are calculated in the range 1.036- 2.270 ppm, and in the CH₂ groups are in the range 1.324 - 2.713 ppm. The chemical shift value of the H atom bonded to C3 is calculated in the range 3.668 - 2.949 ppm and observed at 4.284 ppm.

There are seven carbon atoms in the title molecule, and the ¹³C NMR spectrum of the NAM exhibits seven signals. The signal at 173.36 ppm is assigned to the C4 carbon atom of the carboxyl group computed as in the range 178.167 - 173.800 ppm. As would be expected, ¹³C NMR chemical shifts for C4 and C2 atoms are calculated as higher than the other C atoms due to the electronegativity properties of O and N atoms. As can be seen from Table IV, the theoretical ¹³C chemical shift results for NAM are generally closer to the experimental ¹³C shift data.

3.4.Non-linear optical (NLO) analysis

The electric dipole (hyper) polarizabilities of a molecule are a measure of the ability to respond to an electric field (E) ³³ and determine the strength of molecular interactions (long-range intermolecular induction and dispersion forces), the cross sections of different scattering, collision processes ³⁴ and the nonlinear optical properties of the system ³⁵.

In the presence of the electric field, the expectation value of the electric dipole moment is the sum of a permanent dipole moment and the contribution induced by the field:

In this expression, α is the linear polarizability, and β is the first hyperpolarizability (else, sometimes, second-order or quadratic hyperpolarizability).

The relation between the three Cartesian components of the dipole moment vector (μ⃗) and the three Cartesian components of the electric field vector (E⃗) requires nine proportionality factors, therefore α is a second rank tensor that can be described by a 3 x 3 matrix with the 9 components. The second interaction involves evaluating the effect on the dipole moment of combinations of Cartesian components of the field; therefore, β is the third rank tensor that can be described by a 3 x 3 x 3matrix with the 27 components. According to Kleinman symmetry, α can be reduced into 6 components (αxy=αyx, αxz=αzx, αzy=αyz) and β can be reduced into 10 components (βxyy=βyxy=βyyx=βyyz=βyzy=βzyz...) ³⁶. In the lower tetrahedral point group, the Gaussian 09W output file printout of the ?? matrix is αxx, αxy, αyy, αxz, αyz, αzz, and β matrix is βxxx, βxxy, βxyy, βyyy, βxxz, βxyz, βyyz, βxzz, βyzz, βzzz.

For the title molecule, we use the following expressions to calculate. The dipole moment,

The isotropic polarizability,

The anisotropy polarizability,

And the magnitude of the first order hyperpolarizability tensor (⟨β⟩) is defined in terms of three axes as:

where, in general, components equation of β can be calculated using the following equation:

The complete equation for the β in terms of Cartesian components leads to:

In this study at DFT with 6-311++G(d,p) basis set, based on the finite field (FF) approach, parameters such as the total static dipole moment (μ), the component of the dipole moment (μi(i=x,y,z)), the isotropic polarizability (⟨α⟩), the anisotropy of the polarizability (Δα), the first order hyperpolarizability (⟨β⟩) are calculated by using B3LYP and HSEH1PBE functionals for NAM and collected in Table V. Also, Table V collects these parameters for two reference molecules, i.e., urea and para-nitroaniline (pNA). Urea and pNA are well-known prototypical donor-acceptor organic standards with large hyperpolarizability ^37-42. The first-order hyperpolarizability values for NAM are higher than urea and pNA molecules.

All the tensors values of the Gaussian 09W program output file are reported in the atomic system of the unit (a.u.) and therefore the calculated values are converted into electrostatic units (esu) (for ⟨α⟩ and Δα1 a.u.=0.1482×10-24 esu and for ⟨β⟩ 1a.u.=8.6393×10-33 esu).

3.5.HOMO-LUMO gap (HLG) analysis

The terms HOMO and LUMO are shorthand for the highest occupied and lowest unoccupied molecular orbitals, respectively. HOMO is the orbital of the highest energy for a molecule that contains electrons, and the empty molecular orbital that is closet in energy to the HOMO is called the LUMO. The HOMO and LUMO are the frontier orbitals: the frontier is the site of much of the reactive and spectroscopic activity of the species.

The DFT calculations that are the main working horse for ground-state properties such as atomic structures and binding energies significantly underestimate band gaps in particular the Kohn-Sham eigen energy. In prior studies, band structures predicted by the DFT method are reported to match experimental observations ⁴³.

Ionization energy is the energy required to remove an electron from a neutral atom. The first ionization energy can also be defined as the energy to remove one electron from a neutral atom, to make an ion with a positive charge. Electron affinity is to do with the energy required to add an electron to a neutral atom to become a negative ion. To evaluate the relative reducibility of the title compound, ionization potential and electron affinity were calculated from differences of total energies of the neutral (E_NEUTRAL)and ionic systems (E_CATION, E_ANION) obtained from optimized molecular configurations using the following equations.

The ionization potential,

The electron affinity,

The restricted calculation was used in computing the total energy for the neutral ground state, whereas the unrestricted model was used for cations and anions.

According to Koopmans’ theorem, the first ionization energy directly relates to removing an electron from the orbital is given by the negative value of the energy of the orbital (IP=-EHOMO) if the wave function relaxations are ignored, as calculated within the Hartree-Fock theorem ⁴⁴. In the literature, this theorem has become generally accepted.

Based on the HOMO and LUMO energy for the title molecule, we use the following expressions to calculate.

The electronegativity:

The chemical potential:

⁴⁵.

The hardness:

^46-48.

The softness:

The electrophilicity (in terms of chemical potential and hardness):

The single point energies and frontier molecular orbitals (FMOs) were determined according to quantum chemical calculations, and in these calculations, molecular orbital 51 (the HOMO) is described by as much as 363 molecular orbital coefficients, each of the thirteen hydrogen atoms contributing 7, the three oxygen, seven carbon, and nitrogen atoms contributing 22 and sulfur contributing 30 basis functions. The quantum chemical parameters of the molecule are summarized in Table VI.

The HOMO which is the outermost orbital containing electrons and its vicinal orbital, play an important role in electron donor, while the LUMO, which is the innermost orbital containing free places to accept electrons and its vicinal orbital, play an important role in electron acceptor. The energy value of HOMO was computed as -6.364 eV (B3LYP), -6.180 eV (HSEH1PBE) and LUMO as -0.899 eV (B3LYP), -1.006 eV (HSEH1PBE). The HOMO-LUMO energy gap, which reflects optical and electric properties and chemical activity of the molecule was calculated 5.464 eV (B3LYP) and 5.174 eV (HSEH1PBE); both the values were strongly supported the previous work (5.2 eV ²⁷). To understand the bonding scheme and facilitate discussion of the transitions of the title compound, contour plots of FMOs, HOMO-1 to LUMO+1, are presented in Fig. 3 for the molecule in the gas phase. Thered and green colors of the molecular orbital’s plot show the positive and negative phases, respectively. In the NAM, the HOMO represents the charge density localized over the side chain (-C₅H₂SC₆H₃C₇H₂) unit attached to a C3 atom; by contrast, the LUMO is located over the carboxyl group unit.

Figure 3 The FMOs, energies (in eV), and HOMO-LUMO energy gaps of NAM calculated at B3LYP 

In order to obtain the total density of the state (DOS) curve of NAM as shown in Fig. 4, the output which extracts data from Gaussian .log file was analyzed and plotted as a graph using the Gauss Sum 3.0 program ⁴⁹.

Figure 4 DOS spectrum of NAM using B3LYP/6-311++G(d,p) level in the range of -20 to 15 eV. 

3.7.Molecular electrostatic potential

The electrostatic potential V(r⃗) at any point r⃗ for a molecular system having an electronic density function ρ(r⃗) is given by:

in which Z_A is the charge on nucleus A, located at R⃗A. In this expression, the two terms represent the nuclear and electronic contributions to the potential, respectively.

The electrostatic potential is a physical observable, which can be determined experimentally by diffraction methods (50) and computationally. The Gaussian program calculates the potential at the points that located on the molecule’s size on the ρ(r⃗) isodensity surface and then according to potential assigns colors to these points. In this way, MEP surface maps are surveyed. As is well known, MEP surfaces are useful diagrams that illustrate the charge distributions of molecules three-dimensionally. These maps allow us to visualize the charge distributions, charge related properties, size, and shape of molecules. Moreover, MEP provides interpreting and predicting relative reactivities sites for the electrophilic and nucleophilic attack, studies of the biological recognition process, hydrogen bonding interactions, molecular cluster, and crystal behavior, and the correlation and prediction of a wide range of macroscopic properties ^51-55.

Figure 5 presents the MEP surface of the molecule under investigation is composed by using B3LYP/6-311++G(d,p) level of theory and a value of 0.0004 a.u. for the isodensity surface. On the map, the most negative (the lowest) and positive (the highest) electrostatic potentials are colored red and blue, respectively, and intermediate potentials are colored intermediate color spectrum.

Figure 5 MEP surface of NAM using B3LYP/6-311++G(d,p) level of theory. 

Furthermore, the MEP map provides a visual method to understand the relationship between the structure and activity of the molecule. It is used to identify electrophilic and nucleophilic sites of a molecule. It can be seen from Fig. 5, the obtained electrostatic potential is composed of the positive electrostatic potential around the O1 atom in the peptide group, which is the most reactive site for nucleophilic attack. The negative electrostatic potential is mainly localized around the N-H in the peptide group region and O3-H in the carboxyl group, which is the possible site for electrophilic attack. The remaining green areas of the molecule (C-C bonds) are surrounded by close to zero electrostatic potential.