3.1.Structural properties

The double perovskite Sr₂TiCoO₆crystallizes in an ideal cubic structure as shown in Fig. 1, with space group Fm3¯m (225) according to Hermann-Maguin convention, where Sr atoms occupy 8c (0.25, 0.25, 0.25), Ti at 4b (0.5, 0.5, 0.5) sites, Co on 4a (0, 0, 0) and O at 24e (0.25, 0, 0) of cubic unit cell ²⁶. The experimental lattice parameters have been optimized using Birch-Murnaghan’s ²⁷ equation of state by fitting energy versus cell volume in nonmagnetic (NM) and ferromagnetic (FM) cases. From Fig. 2 it is clearly shown that the lowest energy corresponds to the ferromagnetic phase with an optimized lattice parameter of 7.76 Å. The calculated ground state parameters which include bulk modulus (B₀), lattice constant (A), and pressure derivative of bulk modulus are displayed in Table I. It is clear that the calculated lattice constant of Sr₂TiCoO₆ mentioned in Table Iis close to the available experimental data ¹⁸. Also, the deviation of calculated oxygen parameter x from the ideal value of 0.25 is assumed in the simple perovskite structure. Since there is no available experimental or theoretical data to compare the bulk modulus and its derivative, our results are predictive and can help potential investigations.

Figure 1 Crystal structure of double perovskite Sr₂TiCoO₆. 

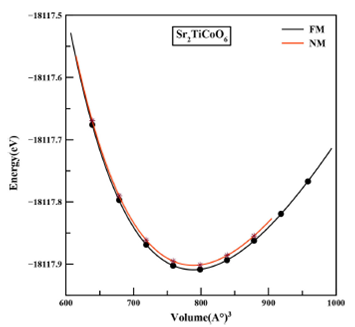
Figure 2 Structural optimization plots of Sr₂TiCoO₆ in ferromagnetic (FM) and non-magnetic (NM) phases. 

The stability of the material was also checked by calculating the tolerance factor (τ) as:

Where r_Sr is the ionic radius of the Strontium atom, r₀ is the ionic radius of the oxygen atom, r_Ti is the ionic radius of the Titane atom, and r_Co is the ionic radius of the Cobalt atom. Materials with τ in the range of 0.9 to 1.0 have a perfect cubic structure, and τ greater than 1.0 results in a hexagonal structure ²⁸. The value of the tolerance factor computed for Sr₂TiCoO₆is equal to 0.92.

3.2.Electronic and magnetic properties

The spin-polarized electronic band structures of Sr₂TiCoO₆along the high-symmetry Brillouin zone points have been studied using GGA and mBJ approximations, as presented in Fig. 3. In order to have the correct estimation of the band-gap in spin up channels which is usually underestimated by GGA, mBJ has been used. First, in the case of the spin-up channel, we can distinguish the Fermi level in the middle of the band-gap showing the semiconducting nature. While for spin-down states it is clear that the fermi level is completely occupied, presenting the metallic nature in both approximation methods. As seen from the band profiles using both approximated schemes, half-metallicity is achieved, and the studied material can find various applications in spin-based devices. The value of the gap using GGA is different from the one using mBJ, and it is equal to 1.18 eV, 2.14 eV, respectively, at symmetric points ‘X’ and ‘Γ’, generating an indirect band-gap. The gap increases as we go from GGA to mBJ.

Figure 3 The band structures of Sr₂TiCoO₆ for both spin channels with GGA and mBJ approaches. 

The mechanism of magnetism in the double perovskite (DP) compound has been extensively discussed ^29,30,31,32. In the crystal structure shown in Fig. 1, the magnetism in the material can be understood in terms of an ionic description where the Co5+ (3d³) and the Ti4+ (3d²) ions occupy alternating ionic positions along the three axes of the larger cube with consecutive anti-parallel spin alignment, suggesting a total magnetic moment of 1 μB per formula unit (f.u.) for the system. However, the half-metallic states and consequently the magnetic moments are critically dependent on the perfect ordering of the Co and Ti sites. In order to unravel the origin of the magnetism in the Sr2TiCoO6 series, we have first investigated the electronic density of states (DOS) of this compound. Figure 4 shows the DOS as obtained in spin-polarized DFT calculations within GGA-mBJ method. The peaks below -6.2 eV to about -4.5 eV are a mix between the Co-eg d and Co-t2g d states. While the peaks below -1.2 eV refer mostly to oxygen contributions. The peaks crossing the Fermi level and ranging from -1.2 eV to about 0.3 eV belong mainly to Co-t2g d states and some slightadmixture of oxygen p states. The presence of approximate cubic symmetry of the octahedral coordination of oxygen atoms around the transition metal sites results in a splitting of the d levels into d-t2g and d-eg orbitals. The Co-t2g peaks are partially filled in the minority spin channel, while the Co-eg, Ti-t2g, and Ti-eg bands remain empty.

The occupied part of the bands near the Fermi level in the majority spin channel [see Fig. 4] is mainly composed of Co d states, which hybridize with the oxygen p states. The narrow bands lying directly above the Fermi level covering an energy range of about 0.8 to 2.2 eV are mostly from Co-eg and Ti-t2g contributions, while the Ti-eg bands are high in energy.

Figure 4 Combined total and partial density of states for Sr₂TiCoO₆ using GGA-mBJ approaches. 

Furthermore, the calculated individual, interstitial, and total magnetic moments have also been calculated with GGA and mBJ. Our compound has a ferromagnetic nature with a total magnetic moment of nearly 1 μB which is the summation of the partial moments from various atoms and the interstitial sites. Sr, Ti, and O atoms show a very small contribution to the total magnetic moment, which is almost negligible as displayed in Table II. The main contributions to the total magnetic moment come from the Co atom, where its partial moment is of 0.718 μB (GGA) and 0.6662 μB (mBJ). The FM nature for Sr₂TiCoO₆is predominately due to cobalt atoms. The main source of magnetization in this compound is from unfilled Co-3d orbitals. The positive value of the magnetic spin moment is due to cobalt, whereas the low negative value is attributed to Titane. Comparing to other experimental reported results it is shown that antiferromagnetic-type coupling dominates over weak ferromagnetic coupling in the STC system ³³.

3.3.Elastic and mechanical properties

Elastic properties not only provide a decent and dynamic suggestion of the system but also give us better knowledge of the material strength for its technological applications. These constants give concrete and necessary comprehension of solid mechanical stability under different forces.

In this study, we investigated the mechanical and elastic properties of Sr₂TiCoO₆. The elastic constants were obtained by calculating energy about the tetragonal and rhombohedral strain ³⁴. Only three independent elastic constants (C₁₁, C₁₂, and C₄₄) are used for materials with cubic symmetry. The values of these elastic constants under ambient conditions were determined and shown in Table III. For cubic structures under ambient condition the stability criteria is: (C₁₁ - C₁₂ > 0, C₁₁ > 0, C₄₄ > 0, (C₁₁+2C12 > 0, C₁₂ < B < C₁₁, where C₁₁ stands the compressive resistance along the direction of 𝑋-axis. Also, the value of C₁₁ indicates a larger value as compared to other values, which suggests the incompressible essence of the material, C₁₂ indicates transverse strain, C₄₄ is shear modulus and B represents bulks modulus. The calculated values of elastic constants strictly follow the generalized mechanical stability criteria³⁵.

Additionally, these elastic parameters are related to other mechanical properties through empirical expressions displayed as ³⁶.

E=9BG3B+G,B=C11+2C123,ν=3B-2G2(2B+G)A=2C44C11-C12.

Where E and B are Young’s and Bulk’s moduli respectively. v is a Poisson’s ratio and 𝐴 is an anisotropy ratio which are listed in Table III. Bulk modulus describes the stiffness of a material, the higher the value of B, the higher its stiffness resistance is. The calculated value of bulk modulus of Sr₂TiCoO₆is largely showing strong resistance to volumetric change caused by applied stress. The shear modulus (G), which characterizes the calculated plastic twist of material, has been obtained from the Voigt-Reuss-Hill approximation ^37,38 using the arithmetic mean of Voigt, G_V, and Reuss G_R, presented in Table III and calculated as:

GV=C11-C12-3C445=137.08,GR=5C44(C11-C12)(4C44+3&#091;C11-C12&#093;)=135.85,G=12(GV+GR)=136.46.

The value of Young’s modulus (E) was obtained from the bulk modulus (B) and the shear modulus (G) ⁸. As (E) defines the strength of the material, the higher the value of (𝐸), the higher its strength is. The obtained value of (E) was calculated to be 334.05 GPa, which is large enough, and therefore Sr₂TiCoO₆acts as a hard material.

Poisson’s ratio ‘v’ is used to evaluate the ductility and brittleness of a compound. The material has a ductile nature if its value is greater than 0.26; otherwise, the material is considered to be brittle. Table IIshows that Poisson’s ratio for Sr₂TiCoO₆was found to be lower than 0.26, which confirms its brittle nature. Poisson’s ratio ‘𝜈’ also gives knowledge about the estimation of bonding nature ^39,40 in a material. According to this limit, the type of material bonding will be ionic if ≈0.25, covalent if ≈0.10, and metallic if ≈0.33. For our compound, 𝜈 is found close to 0.25 and thus major bonding in these materials is ionic.

The Pugh’s ratio ⁴¹ is another stability criterion to define whether the material is ductile or brittle. Its numerical or index value is 1.75.B/G>1.75 indicates the ductile nature while the value of B/G<1.75 is associated with the brittle character of the material. From the observed data, the computed value of B/G for Sr₂TiCoO₆compound is < 1.75. Consequently, it has a brittle nature.

The brittle nature was also verified from Cauchy’s pressure relation ⁴² defined as (C₁₂-C₄₄). A positive value indicates that the material is ductile otherwise the nature is identified as brittle. For Sr₂TiCoO₆it is clear that Cauchy’s pressure is negative which emphasizes its brittle nature.

Zener’s anisotropy factor (A) describes the degree of the elastic anisotropy of the solid. For an isotropic material, the anisotropy factor (A) is equal to one, while any different value shows anisotropy ⁴³. From Table III, it was found to be 0.82 (less than 1), signifying that the material has elastic anisotropic nature.

There are no theoretical or experimental data on the elastic properties of this compound for which we can compare our work. We believe that in the future, our work can encourage further research in this direction.

The melting temperature is also a further thermodynamic quantity which has been calculated using the following empiric expression ⁴⁴ as described below.

Tm(K)=[553  (K)+(5.911)C11]  GPa ±300  K

The corresponding observed value for the present alloy is 2929.81 ± 300 K and thus suggests that the material has a strong capability to maintain its crystal structure over a large range of temperatures.

3.4.Thermoelectric properties

Thermoelectric materials (TE) have the potential to convert waste heat into usable energy ⁴⁵. Because of their energy convergence management, these materials are currently being studied at faster levels rather than other technologically appropriate materials.

To explore the electronic transport properties of Sr₂TiCoO₆layered perovskite, we have made use of semi-classical Boltzmann theory as employed in BoltzTraP code ²⁵. In order to have potential thermoelectric properties in a material, it needs to have a large value of electrical conductivity ( σ/τ), a large value of Seebeck coefficient (𝑆), and very low electronic thermal conductivity ( κe/τ).

In this article, the thermoelectric parameters in the range of temperatures from 100 K to 1000 K have been reported, in Fig. 5(a). The electrical conductivity per relaxation time (σ/ τ) as a function of temperature for Sr₂TiCoO₆is represented, we can observe that electrical conductivity increases with increasing temperature until reaching a maximum value of 2.5488 X 10¹⁸ (Ωms)^-1 at 1000 K. Electrical conductivity is about 19.189 x 10³ at low temperatures (100 K). The variation of the Seebeck coefficient (S) as a function of temperature is shown in Fig. 5b). It is clearly apparent from the plot that the Seebeck coefficient (S) decreases to a minimum of 393.15 μV/K with an increase in temperature. The Seebeck coefficient is positive, meaning 𝑝−type conduction. At 100 K, a maximum value of 3068.24 μV/K was obtained. Figure 5c) depicts the response of electronic thermal conductivity (κe/τ) within 100 K and 1000 K for Sr₂TiCoO₆. The figure clearly shows that the nature of (κe/τ) is increasing with increasing temperature. The value of (κe/τ) increases from 18.09 W/mKs at 100 K to 5.58 x 10¹⁴ W/mKs at 1000 K. In order to estimate the thermoelectric efficiency of Sr₂TiCoO₆, we calculated the fluctuation of the power factor over a large temperature range as shown in Fig. 5d). We can observe that PF increases slightly with rising temperatures, from 1.806 x 10¹¹ (W.m^-1.K^-2s) at 100 K until reaching the value of 3.939 x 10¹¹ (W.m^-1.K^-2s) at 1000 k. The thermoelectric values found for Sr₂TiCoO₆are definitely higher to those reported experimentally for Ba_xSr_2-xTiCoO₆ with x = 0.0, x = 0.10, x = 0.15, and (d) x = 0.2 ⁴⁶. The obtained results from the first principles calculation reveal that Sr₂TiCoO₆is a promising thermoelectric material.

Figure 5 a) Variation of electrical conductivity (σ/ τ), b) Seebeck coefficient (S), c) electronic thermal conductivity (S), d) power factor (PF) as a function of temperature for the Sr₂TiCoO₆ compound.