1. Introduction
The studies of the relativistic generalization of the harmonic oscillator has drawn
much attention in recent years. The wellknown relativistic model of the harmonic
oscillator was revived by Moshinsky and Szczepaniak [1], who gave it the name of Dirac oscillator (DO) because, in the
non-relativistic limit, it becomes a harmonic oscillator with a very strong
spin-orbit coupling term. The Dirac relativistic oscillator is an important
potential both the theoretical and application implications. It was for the first
time studied by Ito et al. [2]. They considered a Dirac equation in which the momentum
The unification between the general theory of relativity and the quantum mechanics is
one of the most important problems in theoretical physics. This unification predicts
the existence of a minimal measurable length on the order of the Planck length. All
approaches of quantum gravity show the idea that near the Planck scale, the standard
Heisenberg uncertainty principle should be reformulated. The minimal length
uncertainty relation has appeared in the context of the string theory, where it is a
consequence of the fact that the string cannot probe distances smaller than the
string scale
This commutation relation leads to the standard Heisenberg uncertainty relation
which clearly implies the existence of a non-zero minimal
In this direction, some remarks can be made about Eqs. (1) and (2): (i) according to
the woks of [14-18], one important observation was that various observable
effects of the minimal length uncertainty relation are non-perturbative in the
deformation parameter β, (i.e., contain all orders
in β) even though β appears only to linear order
in Eqs. (1) and (2) [16-18] . (ii) In Ref. [15],
the authors study the effect of the minimal length on the thermal properties of a
Dirac oscillator when the position and momentum obey Eq. (1), and studied the
possible constraint that can be placed on β. By using the
properties of the Epstein zeta function, this study leads to a minimal length in the
interval of 10−16
< ∆x < 10−14 m with the following
physically acceptable condition β > β
0 = (1/m
2
c
2). (iii) Kempf [10,11,19]
has shown that Eq. (1) follows naturally when the canonical commutation relation
between position and momentum operators is modified according to the Eq. (1). So, we
may select the position
One should note that the construction of models in these spaces would not be an easy
task as the operators
According to the Kempf’s prescription [10-12, 19], the position and momentum operators satisfying Eq. (1) can be also represented by
where the operators x and p satisfy the canonical
commutation relation
The parameter γ appears in both Eqs. (4) and (5) is an arbitrary constant which does not affect the observable quantities; its choice determines only the weight function in the definition of the scalar product [22]. In this work, we have opted with the Kempf method, and so we chose γ = 0.
Nowadays, the reconsideration of the relativistic quantum mechanics in the presence of a minimal measurable length have been studied extensively. In this context, many papers were published where a different quantum system in space with Heisenberg algebra was studied. They are: the Abelian Higgs model [19], the thermostatics with minimal length [23], the one-dimensional Hydrogen atom [24], the Casimir effect in minimal length theories [25], the effect of minimal lengths on electron magnetism [26-28], the solutions of a two-dimensional Dirac equation in presence of an external magnetic field [29], the non-commutative phase space Schrödinger equation [30], and the Schrödinger equation with Harmonic potential in the presence of a magnetic field [31].
The study of NC spaces and their implications in physics is an extremely active area of research. It has been argued in various instances that non-commutativity should be considered as a fundamental feature of space-time at the Planck scale. On the other side, the study of quantum systems in an NC space has been the subject of much interest in past years, assuming that non-commutativity may be, in fact, a result of quantum gravity effects. In these studies, some attention has been paid to the models of NC quantum mechanics (NCQM). The interest in this approach lies on the fact that NCQM is a fruitful theoretical laboratory where we can get some insight on the consequences of non-commutativity in field theory by using standard calculation techniques of quantum mechanics. Various NC field theory models have been discussed as well as many extensions of quantum mechanics. Of particular interest is the so-called phase space noncommutativity, which has been investigated in the context of quantum cosmology, black holes physics, and the singularity problem. This specific formulation is necessary to implement the Bose-Einstein statistics in the context of NCQM (see [32-38]).
In addition, investigating the influence of the minimal length assumption on the energy spectrum of quantum systems has become an interesting issue primarily for two reasons. First, this may help to set some upper bounds on the value of the minimal length. In this context, we can cite some studies of the hydrogen atom and a two dimensional Dirac equation in an external magnetic field. Moreover, the classical limit has also provided some interesting insights into some cosmological problems. Second, it has been argued that quantum mechanics with a minimal length may also be useful to describe non-point-like particles, such as quasi- particles and various collective excitations in solids, or composite particles (see Ref [25] and references therein).
The purpose of this work is to investigate the formulation of a two-dimensional Klein Gordon oscillator (KGO) in the presence of a magnetic field by solving fundamental equations in the framework of relativistic quantum mechanics with minimal length in the NC space. To do this we first mapped the problem in question into a commutative space by using an appropriate transformations. Then, we solved it in the presence of a minimal length.
The paper is organized as follows. In Sec. 2, we solve the KGO in the presence of magnetic field in noncommutative phase space. Then, in Sec. 3, we study this problem in the framework of relativistic quantum mechanics with minimal length. Finally, Sec. 4 will be a conclusion.
2. The solutions within habitual quantum mechanics in NC space
To begin with, we note that the non-commutative phase space is characterized by the fact that their coordinate operators satisfy the equation [33-38]
where Θ
µν
is an antisymmetric tensor of space dimension. In order to obtain a theory
which includes the aspects of being unitary and causal, we choose Θ
0ν
= 0 , which implies that the time remains as a parameter and the
non-commutativity affects only the physical space. The noncommutative models
specified by Eq. (1) can be realized in terms of a
Since the system in which we study is two-dimensional, we limit our analysis to the xy plane, where the noncommutative algebra is written by
where ϵ ij is the two-dimensional Levi-civita tensor. Instead of solving the NC Klein-Gordon equation by using the star product procedure, we use Bopp’s shift method, that is, we replace the star product by the usual product by making a Bopp’s shift
Hence, in the two dimensional non-commutative phasespace, Eq. (9) becomes
In this case, the two-dimensional Klein-Gordon oscillator , in commutative space, which is written by
is modified and transformed into
with
Here we have used that
In the literature (see Ref [6] and references therein), the upper bound on the value of the coordinate commutator found is Θ ≤ 4×10−40 m2. So, as an approximation, all terms with the square of Θ have been neglected.
Now, by putting Eqs. (13) and (14) in (12), we obtain
In order to solve the last equation, and for the sake of simplicity, we bring the problem into the momentum space. Recalling that
and when passing onto polar coordinates [9]
Eqs. (17) and (18) become
Putting Eqs. (20) and (21) in Eq. (16), the last equation can be written explicitly in polar coordinates by
where
With the help of the following relation [39]
Eq. (22) is transformed into
with
Now, noting that [39]
then the differential equation
is transformed into the Kummer equation
which by using, instead of p, the variable xt = kp 2. The solution of this equation is the confluent series 1 F 1 (α;|l| + 1;t), with
The confluent series becomes a polynomial if and only if α = −n, (n = 0,1,2,).
Thus, following this, we have the solutions
with N = 2n + |l| is the principal
quantum number, and
We can see that the presence of the parameter Θ, in the spectrum of energy, breaks the degeneracy of the energy levels. Furthermore, by taking that Θ = 0 , we reach the exact result of the two-dimensional Klein-Gordon oscillator in Minkowski space-time
This form of energy is in a good agreement with that obtained in the literature (see Ref. [37]).
3. The solutions in the presence of a minimal length
In the minimal length formalism, the Heisenberg algebra is given by [11-22]
where 0 < β ≤ 1 is minimal length and p is magnitude of the momentum. When the energy is much smaller than the Planck mass, β goes to zero and we recover Heisenberg uncertainty principle.
A representation of
By using the Eqs. (36) and (37), Eq. (16) becomes
Now, when we put that
with j = 0,±1,±2,..., the Eq. (38) is transformed into
with
In order to solve Eq. (40), we adopt the following substitution as used by Jana et al., [38]
After these susbsitutions, Eq. (40) becomes
with
with ρ(p) = p −1/2 .
In order to simplify the function V (p), we use the change of variable
In this case, the form V (p) with the new variable q becomes
Consequently, the final form of our differential equation is
where
Thus, Eq. (48) is brought to
with
and where
Finally, we have
where U
0 = α
2 with
In this stage, we can see that Eq. (54) is the well-known Schrödinger equation in a Pöschl-Teller potential with the following potential [39]
and where we have the conditions that (ζ 1 ,ζ 2) > 1.
By comparing Eq. (48) with Eq. (54), we obtain
Now, in order to solve Eq. (48), we introduce the new variable
In this case, Eq. (48) can be rewritten as
With the new wave function φ, defined by
we arrive at
The general solution of this equation is
with
With the condition a' = −n, we obtain
In order to obtain the energy spectrum, it should be noted that in the limit β → 0, the energy spectrum should regenerate to the no-GUP result.
Thus, the exact form of ζ 1 and ζ 2 are
where j ≠ 0.
With the aid of Eqs. (56), (57) and (64), we obtain the final form of the spectrum of energy: it is expressed explicitly by
From Eq. (67), the presence of both β and Θ breaks the degeneracy of our spectrum of energy. In addition, the presence of the spectrum of energy with the parameter β, contrarily to the case of Θ, leads to the dependence of the energy levels on n 2: as mentioned by Nouicer [27], this dependence on n 2 is a feature of hard confinement. Finally, in the limit where β → 0, we reach the following equation
which has the same form as the Eq. (33). The corresponding wave function is
with Nnorm is the constant of normalization.
4. The solutions in the presence of a magnetic field
In a magnetic field, when we choose the potential vectors as
the two-dimensional Klein-Gordon oscillator in non-commutative space is
or in the explicit form as
By using Bopp’s shift method, Eq. (72) is transformed into
Putting Eqs. (36), (37) and (39) in (73), we obtain
with ς 2 = (E 2 - (m 0 c 2)2 /c 2). Following the same procedure as in the above section, we have
or with the new variable q,
In this case, the form of V is
or with the variable q
Where
Finally, our differential equation can be written as
where U
0 = α
2 and
As in the above case, Eq. (78) is the well-known Schrödinger equation in a
Pöschl-Teller potential [39]. with the
constraint that
So, the general solution of Eq. (78) is
with z = sin2 (αq) and where
With the condition a' = −n, and by using Eq. (64), we obtain.
Now, from Eq. (83) the final form of the spectrum of energy is
with
Also, we can see that the presence of both parameters β and Θ with a magnetic field breaks the degeneracy of the spectrum of energy. In addition, the presence of a term on n 2 shows the existence of hard confinement. This dependence is only clear when we introduce minimal length in the problem in question.
Finally, the corresponding wave function is
with Nnorm the constant of normalization.
Now, to achieve a deeper understanding of our spectrum of energy presented by Eq. (84), we have plotted the variation of the positive energy E with quantum number n and magnetic field B for different various situations. As the spectrum of energy is symmetric, any comments on the case of the positive energy can be extended to the case of the negative energy.
Figure 1 shows the behavior of the spectrum of energy versus n by changing the three parameters appearing in the expression for the energy spectrum, i.e, the magnetic field B, the NC parameter θ and the minimal length β. This figure has been depicted for two cases: j = 0 and j = 1. Here, three remarks can be made
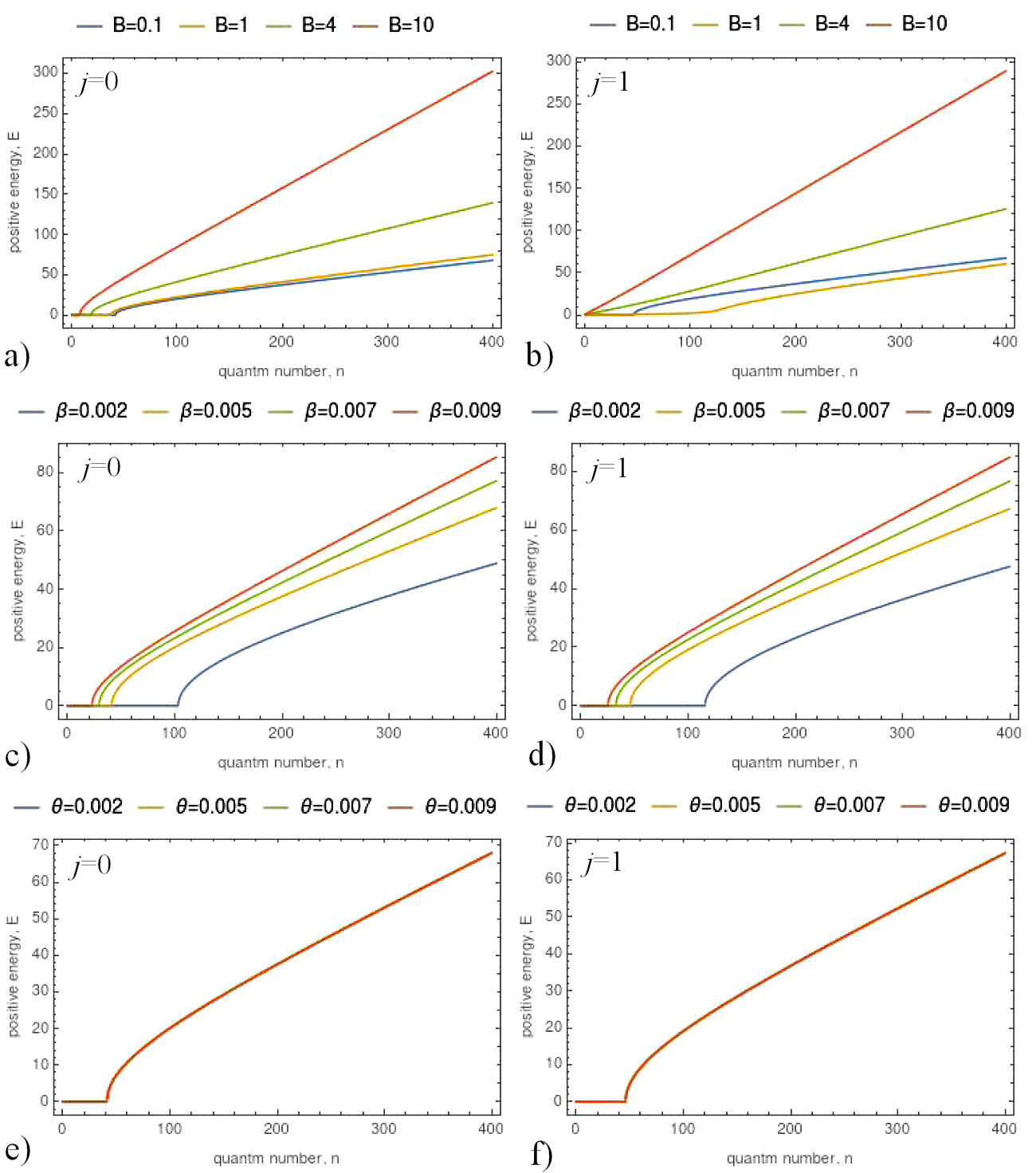
FIGURE 1 The positive energy eigenvalues as a function of the quantum number n. a, b) Variation with respect of B for fixed value of θ = 0.00 and β = 0.005; c, d) variation with respect of β for fixed values of B = and θ = 0.005; e, f) variation with respect of θ for fixed value of B = 0.1 and β = 0.005.
When varying only the magnetic field, one observes that the allure of the spectrum of energy tends to become linear in the high magnetic field regime.
From the variation of β only, we can see that for each value of β we have two regions: first region, the values of the energy are zero until a specific number where the spectrum begin grows. According to this figure, this specific number depends inversely with β.
Now, when varying θ, we see that all curves coincide.
In Fig. 2, we represent the variation of the positive energy levels with magnetic field for four levels n = 0,1,2,3. For each level of energy, we have chosen j = 0,1,2,3. With the exception of the case j = 0, every curve show approximately a linear form with a magnetic field B.
Finally, in order to show that the problem in question has relevance from a physical point of view, we make the following remarks. Firstly, we can mention some studies that showed the existence of a close relation between graphene and the Dirac oscillator model. [6,40-42].
Bastos et al., [33] consider a non-commutative description of graphene. This description consists of a Dirac equation for massless Dirac fermions plus non-commutative corrections, which are treated in the presence of an external magnetic field. They argue that, being a two-dimensional Dirac system, graphene is particularly interesting to test nonommutativity. They find that momentum non-commutativity affects the energy levels of graphene and they obtain a bound for the momentum non-commutative parameter. Their results show that momentum non-commutativity yields interesting results also at low-energies and that its implications are not restricted to quantum cosmology and black holes physics.
In the same context, Falomir et al. [43] employ a simple nonrelativistic model to describe the low-energy excitation of graphene. The model is based on a deformation of the Heisenberg algebra which makes the commutator of momenta proportional to the pseudo-spin. As a result, the resulting Hall conductivity is consistent with the anomalous integer quantum Hall effect found in graphene.
Jallel [44] describes the lattice deformation in graphene under strain effect by considering the spacial-moment coordinates do not commute. Within such framework, he (i) build a new model describing Dirac fermions interacting with an external source that is non commutative parameter dependent, and (ii) the eigenvalues are showing Landau levels in similar way to the case of a real magnetic field applied to graphene.
Iorio and Pais [45], in their paper “Generalized uncertainty principle in graphene” showed that, by going beyond the low-energy approximation for which the dispersion relations of graphene are linear, the corresponding emergent field theory is a specific generalization a Dirac field theory. The generalized Dirac Hamiltonians one obtains are those compatible with specific generalizations of the uncertainty principle. They also comment on the compatibility of the latter with non-commuting positions, and on their possible physical realization.
Thus, following these works and maybe others which are not cited here, we can expect that our study can be regarded as a contribution to the case of graphene by introducing the minimal length in the commutations rules of Heisenberg.
5. Conclusion
In this paper, we have exactly solved the KGO in two dimensions in the presence of an external magnetic field in the framework of relativistic quantum mechanics with minimal length and in the NC space. Firstly, by adopting the same procedure used by Menculini et al. [9], we have solved the problem only in the case of non-commutative space. The results found are in good agreement with those obtained in the literature. After that, we have introduced the minimal length in the problem in question. This introduction has been making as follows: (i) we write the coordinates of the noncommutative space with those in commutative space by using the Bopp shift approximation, and (ii) then we introduce the minimal length in our equation. By these, the problem in question is identified with a Pöschl-Teller potential.
The eigensolutions of the problem in question in a magnetic field are obtained in the presence of a minimal length in non-commutative space. The dependence on theses eigensolutions with the minimum length and the non-commutative parameters is very clear. Furthermore, by comparing the spectrum of energy obtained in our case with those of the same problem in the flat space-time, we can see that the presence of both parameters breaks the degeneracy of the spectrum of energy. In addition, the presence of a term on n 2 in the form of the spectrum of energy shows the existence of hard confinement. This dependence is only clear when we introduce minimal length in the problem in question. Finally, In the limit where β → 0 and Θ → 0 tend to zero, we recover well the results obtained in the literature.











 nova página do texto(beta)
nova página do texto(beta)



