1. Introducción
Los sistemas de telecontrol en tiempo real a través de Internet presentan un tiempo telecontrol TTc,k, constituido por los tiempos de ejecución ck y transporte τk el cual a su vez está conformado por los tiempos de transmisión τTx,k y recepción τRx,k. Sin embargo, estos sistemas son susceptibles a diversos factores (tal y como la infraestructura, horario, fecha, códigos informáticos maliciosos, interferencias electromagnéticas, normas de comunicación o protocolos) que afectan al tiempo de telecontrol [1] repercutiendo directamente a la dinámica del tiempo de respuesta total de los equipos involucrados, lo que conlleva a formular modelos matemáticos capaces de imitar el comportamiento de los tiempos involucrados a partir de la extracción de sus propiedades básicas expresadas en un conjunto de atributos matemáticos.
Se han encontrado trabajos en donde se proponen modelos que han servido para encontrar medidas de desempeño de interés como el retardo promedio, variaciones en el retardo, tiempo de arribo, tiempo de transmisión y recepción (Round trip time), ocupación en tiempo de la memoria en los circuitos de interconexión, tiempos de codificación, etcétera, los cuales conforman principalmente al tiempo existente en el tráfico de datos en el medio de comunicación por internet.
Para cuantificar los tiempos de codificación, compresión y de transmisión de una señal digital de video, en [2] se presenta un modelo que ha servido para tal fin mediante el uso de técnicas autoregresivas y procesos markovianos, justificando la necesidad de modelar el tráfico de datos en función de la naturaleza de la señal audio visual. En [3], se presentó el modelado del retardo del tiempo de transmisión en la tecnología inalámbrica de comunicación Bluetooth 2.0, en donde se utilizó una arquitectura cliente-servidor programada en lenguaje C utilizando el protocolo BlueZ, en donde el receptor calcula el tiempo transcurrido desde el inicio de la transmisión de los datos hasta el instante de recepción, tomando en consideración el número de bits de transmitidos, así como el tipo de modulación empleada.
En el trabajo de [4] se realiza el análisis de los modelos de tiempos de transmisión de datos en el tráfico para redes de banda ancha basado en diversos protocolos y para el caso específico del protocolo TCP se menciona que se han usado modelos poissonianos para los cuales, debido a su estructura, subestiman la variabilidad de los tiempos de la transmisión de paquetes, lo que permitió concluir que lo hace impropio para su modelado de tráfico con el protocolo mencionado. En tanto que en trabajo de [5] se realizó una revisión de los modelos de tráfico y control de redes de comunicaciones, observaron que los procedimientos actuales en control de redes se basan en modelos de tráfico acotados, definidos por la tasa pico y la tasa media, y son efectivos para el diseño basado en el sobredimensionamiento, con altas tasas de transmisión y poca memoria para los buffers de espera. Pero si es considerada la variabilidad de los tiempos involucrados, los autores sugieren la investigación basada en la aplicación de técnicas de procesamiento estadístico de señales para monitorear y predecir el desempeño de la red, de manera que se puedan tomar decisiones de control más oportunas y efectivas.
Es por eso que en este trabajo de investigación se midieron, caracterizaron estadísticamente, modelaron y reconstruyeron a los tiempos de transporte (transmisión y recepción) y los tiempos de ejecución o procesamiento remoto en un sistema de telecontrol en tiempo real por Internet; como objeto de estudio se planteó un esquema cliente - servidor en donde se coloca una planta controladora y una planta controlada respectivamente (ver figura 1), que sirvió de base para modelar y reconstruir los tiempos involucrados en la transmisión y recepción de datos a través de técnicas de filtrado digital estocástico.
Para lograr el objetivo del trabajo, se desarrolló un banco de pruebas para la medición y estudio de los tiempos involucrados en la simulación de un proceso de control, el cual fue basado en una arquitectura de software de un esquema multicliente-servidor multiplataforma (QNX-Windows) utilizando los protocolos de comunicación TCP e IP.
Posteriormente se procedió a caracterizar estadísticamente y reconstruir los tiempos de ejecución y los tiempos de transmisión y recepción (tiempos de transporte) existentes en el proceso de telecontrol simulado.
La reconstrucción de los tiempos de ejecución ck fue hecha a partir de técnicas basadas en el Método de la Variable Instrumental y con Filtrado Digital Difuso. Mientras que la reconstrucción de los tiempos de transporte fue hecha utilizando el Filtrado de Kalman.
La organización de este resumen de tesis queda conformada de la siguiente manera, En la primera sección se presentó la introducción. En la segunda sección se presenta la medición, caracterización y reconstrucción mediante técnicas de filtrado digital de los tiempos de ejecución; en tanto que en la tercera sección se presenta la medición, caracterización y reconstrucción del tiempo de transporte usando el filtro de Kalman. En la cuarta sección se presentan las conclusiones.
2. Medición, caracterización y reconstrucción de los tiempos de ejecución
El tiempo de respuesta del sistema de control en tiempo real depende en gran parte del comportamiento de los tiempos de ejecución ci,k de cada instancia ji,k de cada tarea en tiempo real Ji, por esa razón modelar las instancias y las tareas no es sencillo ya que cada una de ellas necesita una representación de acuerdo a su propia dinámica, pues esta variación hace que los Sistemas de control en Tiempo Real puedan no cumplir con sus plazos di,k , provocando que sean poco predecibles, mal dimensionados o poco tolerantes a fallos [6].
Para dar solución a este problema se plantea reconstruir el comportamiento de la dinámica de los tiempos de ejecución a partir de la medición y caracterización estadística de los tiempos de ejecución ci,k . Entonces, el desarrollo de este trabajo, el tiempo de ejecución ci,k se definió de la siguiente manera.
Definición 1 (Tiempo de ejecución en un sistema de telecontrol en tiempo real)
El tiempo de ejecución ck ∈ R+ en un sistema de telecontrol en tiempo real, es el tiempo en que se procesa la información en el intervalo k ∈ Z+ hasta completarse el procesamiento sin considerar los bloqueos por lectura o escritura en los canales de comunicación, desalojos del procesador u otro tipo de suspensiones.
2.1. Medición de los tiempos de ejecución
Para hacer posible la medición de los tiempos de ejecución de un proceso, se usó la arquitectura de hardware reportada en [7], desarrollando un banco de pruebas en el cual se programaron 3 procesos concurrentes en la simulación de la dinámica de un motor de corriente continua. En la Figura 2 se puede ver el diagrama electromecánico del motor en estudio.
El modelo matemático en espacio de estados de acuerdo a [7] es (1, 2):
Cuyas variables, valores y unidades se pueden observar en la Tabla 1 [7].
Tabla 1 Variables del modelo del motor de corriente continua
| Momento de Inercia | J | 1 kg*m2 |
| Coef. Fricción viscosa | b | 1 N*m*s/rad |
| Cte. Construcción | k a | 0.05 |
| Corriente de campo | i f | 20 A |
| Inductancia de armadura | L a | 0.001 H |
| Resistencia de armadura | R a | 3 Ω |
| Voltaje de referencia | V ref | 110 V |
| Par debido a la carga | T D | 0 - 25 N*m |
| Ganancia del controlador | K | 1.36 - 1.7 |
El modelo discreto que representa el comportamiento del motor fue obtenido mediante el método de diferencias finitas [7]. En (3) se muestra la aproximación numérica para la velocidad angular ωr (k) y en (4) se muestra la aproximación para la corriente de armadura ia (k):
donde T representa el tiempo de muestreo, que para este caso fue de una unidad temporal [ UT]. La respuesta de la velocidad angular ωr(k) y la corriente de armadura ia(k) del motor de corriente continua, se puede observar en la Figura 3.
Para el desarrollo del banco de pruebas, se programaron 3 tareas concurrentes para la simulación de la dinámica de un motor de corriente continua. En donde una tarea en tiempo real designada como J1 hizo el cálculo de la corriente de armadura ik . La tarea en tiempo real J2 realizó el cálculo de la velocidad angular wk . En forma adicional, se propuso aplicar una acción de control de tipo proporcional al modelo discreto del motor de corriente continua (Ver figura 4).
Debido a esto se agregó la tarea en tiempo real J3 que se encarga de calcular el Voltaje de corrección Vk generado por la acción de control proporcional. El valor de Kp mostrado en la figura 4 es la ganancia del controlador K al cual se le puede asignar el rango de valores denotados en la Tabla 1. De tal forma que el esquema de tareas en tiempo real concurrentes para este caso de estudio, se puede ver en la Figura 5.
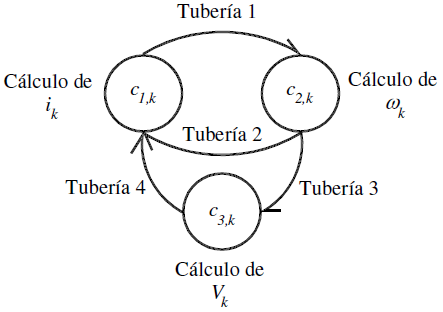
Fig. 5 Esquema de TTR concurrentes y su mecanismo de comunicación en el Sistema Operativo de Tiempo Real QNX 6. 5 Neutrino
Para la medición de los tiempos de ejecución, las consideraciones teóricas se muestran en [8], adicionalmente se usaron los métodos de medición mencionados en [9]. Lo que permitió obtener los tiempos de ejecución c1,k de la tarea en tiempo real J1, que pueden ser visualizados en la Figura 6.
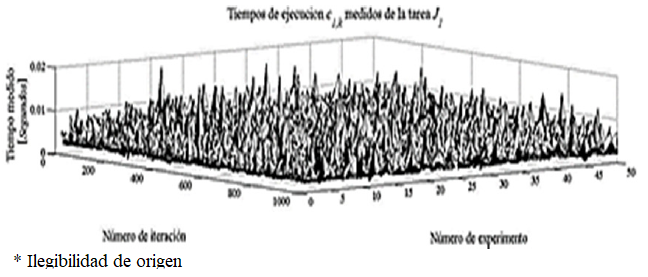
Fig. 6 Medición de los tiempos de ejecución c1,k , (1000 instancias y 50 repeticiones del experimento)
Las tareas J2 y J3 tienen un comportamiento semejante y fueron publicadas en [10].
2.2. Caracterización de los tiempos de ejecución
Para utilizar algún método de reconstrucción para los tiempos de ejecución ci,k de una tarea Ji , se requiere que la información emitida por el sistema sea un proceso estocástico, estacionario en sentido débil, lineal y con función de distribución de probabilidad gaussiana [11].
Un proceso estocástico puede ser estacionario en sentido débil si para todo
tiempo es estable en media
Para la condición de ser estable en autocovarianza
2.3. Reconstrucción de los tiempos de ejecución
Para el modelado del tiempo de ejecución ci,k de las instancias de una TTR Ji con base en [12], en [6] utilizaron un modelo autoregresivo de promedios móviles ARMA de orden (1,1) presentado en [13] para modelar y reconstruir a los tiempos de ejecución de tres tareas en tiempo real, el cual se muestra en (5, 6):
en donde ci,k es el tiempo de
ejecución de la k-ésima instancia de la
i-ésima tarea en tiempo real,
El proceso de estimación de acuerdo a [14], se basa en monitorear los estados que emite el
sistema (en este caso los tiempos de ejecución de una tarea de tiempo real
concurrente) para seleccionar el estimador adecuado y extraer la información
necesaria para describir el parámetro
a. Reconstrucción de los tiempos de ejecución a partir de la estimación del
parámetro
El Método de Variable Instrumental (MVI) es una herramienta que en [16], se comparó con otros estimadores de parámetros, tales como Mínimos Cuadrados Recursivo (MSM) y el Método del Gradiente Recursivo (MGR). En estos trabajos después de realizar un estudio de convergencia local y global, se concluyó que la mejor alternativa para la estimación de parámetros en los sistemas estocásticos con perturbaciones no correlacionadas entre sí es el Método de la Variable Instrumental.
Este estimador de parámetros se utilizó para esta sección para estimar los
parámetros del sistema necesarios para modelar los tiempos de ejecución
ci,k de una instancia
ji,k de una tarea en tiempo
real Ji a partir del modelo
autoregresivo de promedios móviles ARMA de orden (1,1) y fue mostrado en [10] con resultados
satisfactorios. Para la estimación de los parámetros del sistema

Fig. 7 Parámetros estimados
Esto significa que a partir de los estados observables del sistema (los tiempos de ejecución c1,k , c2,k y c3,k de las tareas en tiempo real concurrente J1, J2 y J3) ha sido extraída la información necesaria para estimar el parámetro a del sistema tipo caja negra que representa el comportamiento interno en el que se realiza la ejecución del sistema.
Se observa que la reconstrucción de los tiempos de ejecución c1,k , de la tarea en tiempo real J1 es satisfactoria (Ver Figura 8), pero visualmente no se puede agregar más información para asegurar una reconstrucción exitosa, lo que conlleva a usar criterios como el error cuadrático medio para validar este resultado.
Para el caso del error cuadrático medio entre los tiempos de ejecución reales
ci,k y tiempos de ejecución
reconstruidos
En la Figura 9 se observa que la
reconstrucción del tiempo de ejecución
Pues a medida que se obtengan valores cada vez más pequeños de
Hi,k durante el proceso de
reconstrucción, la diferencia descrita por la ecuación (7), converge a valores
cercanos a 0, lo que permite establecer que la dinámica de los tiempos de
ejecución
b. Reconstrucción de los tiempos de ejecución a partir de la estimación del
parámetro
El filtro difuso es de tipo adaptativo, con una estructura que clasifica sus
respuestas en diferentes niveles de operación. En este caso fue usado para la
selección del parámetro más adecuado
Esto con la finalidad de actualizar los pesos del filtro para describir por medio de un modelo ARMA a la dinámica de una tarea en tiempo real. Cabe aclarar que este desarrollo fue mostrado en [15] con buenos resultados.
Siendo el problema de este trabajo la estimación del parámetro
El error e i,k en la estimación del parámetro se muestra en (10) y la aproximación del parámetro para cada instancia se muestra en (11):
δ es el número total de instancias de un proceso. El objetivo en la selección de
los parámetros es obtener una disminución dinámica del error entre los tiempos
de ejecución reales ci,k y la
reconstrucción de los tiempos
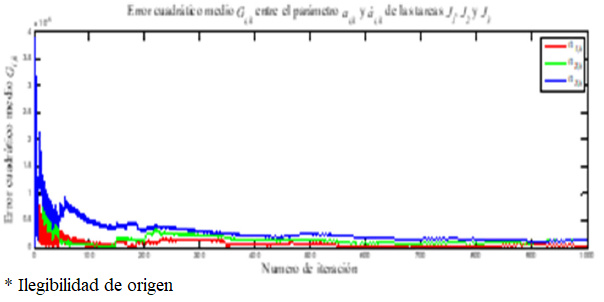
Fig. 10 Error cuadrático medio Gi,k calculado entre el parámetro del
sistema ai,k y el parámetro estimado del sistema reconstruido
En la Figura 10 se aprecia el comportamiento asintótico de las curvas Gi,k y su convergencia a un valor muy cercano a cero, demostrando que el filtro difuso funciona de manera adecuada. En los tres casos pertenecientes a las tres tareas en tiempo real, el error de estimación es de aproximadamente 1×10-3 Segundos; esto muestra que la reconstrucción a través del filtro difuso es satisfactoria y asegura una reconstrucción de los tiempos de ejecución exitosa.
En el filtro difuso se emplean tres niveles de operación representados por
funciones de tipo gaussiano, ya que de acuerdo con [18], por medio de ellas se tiene una mejor
aproximación a un proceso de referencia en comparación con otro tipo de
funciones como las triangulares. En la Figura
11 se presentan los niveles de operación (bajo, medio y alto) para
las TTR J1, J2 y
J3 que permiten obtener la estimación del
parámetro
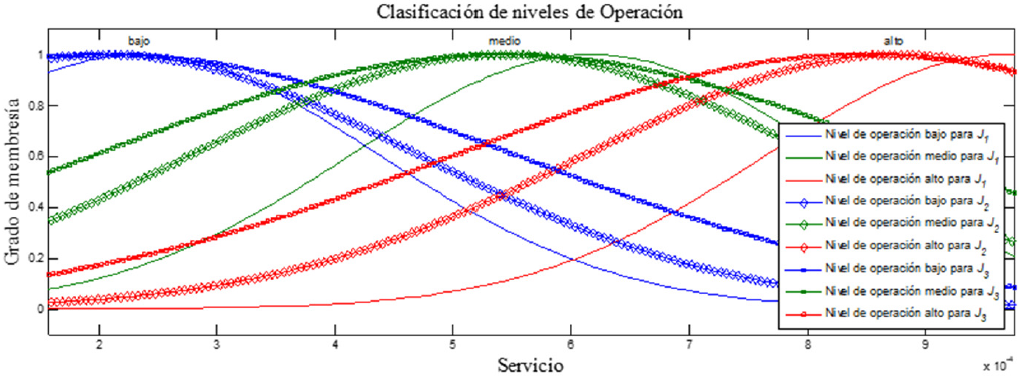
Fig.11. Error cuadrático medio
Gi,k calculado
entre el parámetro del sistema
ai,k y el
parámetro estimado del sistema reconstruido
Para el caso del error cuadrático medio entre los tiempos de ejecución reales
ci,k y tiempos de ejecución
reconstruidos
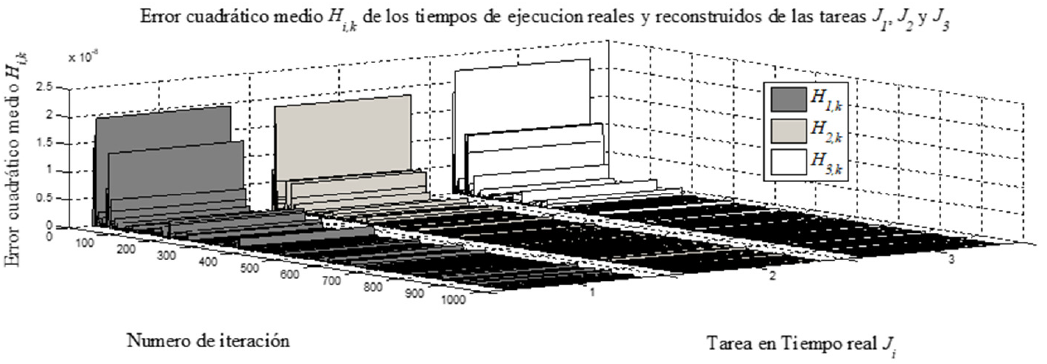
Fig. 12 Error cuadrático medio Hi,k calculado entre los tiempos de ejecución reales y tiempos de ejecución reconstruidos para las Tareas en Tiempo Real J1, J2 y J3 con 1000 instancias
En la Figura 12 y de acuerdo a (8), el filtro tiene una convergencia en casi todos los puntos; se observan las respuestas de los errores H1,k , H2,k y H3,k , destacándose que estos convergen a valores muy pequeños: 1,398×10-7 Segundos, 1,774×10-7 Segundos y 6,525×10-8 Segundos para c1,k , c2,k y c3,k respectivamente, lo que permite describir la calidad de la reconstrucción pues a medida que se obtengan valores cada vez más pequeños de Hi,k durante el proceso de filtrado difuso, la diferencia descrita por la ecuación (32), converge a valores cercanos a 0.
Esto permite establecer que la dinámica de los tiempos de ejecución reconstruidos es similar a la de los tiempos de ejecución medidos, con lo que se valida la reconstrucción lograda a través del algoritmo computacional utilizado.
3. Medición, caracterización y reconstrucción de los tiempos de transporte
La cuantificación de los tiempos de transporte de información en Internet ha sido objeto de estudio debido a que la dinámica de su comportamiento influye en el desempeño de las aplicaciones desarrolladas para trabajar en Internet, debido al incremento en la infraestructura tecnológica, pues provoca un aumento de tráfico soportado por la red global debido a la integración de Tecnologías de la Información y Comunicación (TIC's) en forma de servicios multimedia.
Por esa razón se ha tratado de modelar el tráfico de información en Internet con el fin de mejorar el diseño de redes de acceso y productos de Internet, así como de crear diseños eficientes de esquemas de control de tráfico y de esa manera reducir indirectamente el tiempo de transporte en Internet [20].
El tiempo de transporte xk en un sistema de telecontrol en tiempo real, se puede definir de la siguiente manera:
Definición 2 (Tiempo de transporte en un sistema de telecontrol en tiempo real). El tiempo de transporte τk ∈ R+ en un sistema de telecontrol en tiempo real es la suma algebraica del tiempo de transmisión τTx,k ∈ R+ y el tiempo de recepción τRx,k ∈ R+ en el intervalo k ∈ Z+. De tal manera que:
donde el tiempo de transmisión τTx,k y el tiempo de recepción τRx,k se definen a continuación.
Definición 3 (Tiempo de transmisión en un sistema de telecontrol en tiempo real). El tiempo de transmisión τTx,k ∈ R+ en un sistema de telecontrol en tiempo real es el tiempo en que transcurre en el envío de información desde el cliente de telecontrol hasta el servidor de telecontrol en el intervalo k ∈ Z+.
Definición 4 (Tiempo de recepción en un sistema de telecontrol en tiempo real). El tiempo de recepción τRx,k ∈ R+ en un sistema de telecontrol en tiempo real es el tiempo en que transcurre en el envío de información desde el servidor de telecontrol hasta el cliente de telecontrol en el intervalo k ∈ Z+.
En este sentido la presente sección se encuentra orientada a la reconstrucción de los tiempos de transmisión τTx,k , así como los tiempos de recepción τRx,k , para obtener la reconstrucción del tiempo de transporte τk . Para el caso de la reconstrucción de la dinámica de los tiempos transmisión τTx,k , así como los tiempos de recepción τRx,k, se usará el filtro de Kalman, donde la condición de operación de cualquier filtro es asegurar que el comportamiento de los ruidos asociados a la entrada y salida del sistema sean independientes entre sí, para ello se mide el nivel de dependencia [21, 22].
3.1. Medición de los tiempos de transporte
Para la obtención de los tiempos de transporte de información del protocolo TCP se consideró la arquitectura de software reportada en [7]. La particularidad de la arquitectura de software para el servidor planteada en este trabajo consiste en brindar módulos que pueden usarse para obtener la medición de los tiempos de transmisión τTx,k y los tiempos de recepción τRx,k presentados en el envío y recepción de información.
Aunado a ello, los tiempos de transporte de información medidos pueden ser redireccionadas a una base de datos para su análisis posterior o se pueden enviar, empleando sockets al circuito virtual de comunicación basado en el protocolo TCP, como una cadena de caracteres de 8 bytes. Esta información puede ser leída y/o graficada por clientes basados en otros sistemas operativos. Las mediciones fueron hechas desde las 0 horas del día 8 de Diciembre del 2014 hasta las 0 horas del día 9 de Diciembre del mismo año obteniéndose cerca de 85000 lecturas registradas, cuyos tiempos de transmisión y recepción se pueden apreciar en la Figura 13.
3.2. Caracterización de los tiempos de transporte
Para conocer el nivel de dependencia de variables aleatorias y determinar su dependencia se analizan los ruidos asociados mediante el concepto de momento de covarianza de dos variables aleatorias, de tal manera que si la medida de dependencia es igual a 0 se considera que las dos variables aleatorias son independientes, y en caso de que sea igual a una constante se considera que existe dependencia funcional entre las variables aleatorias [22].
Entonces para el caso de la covarianza del ruido de entrada QTx,k y la covarianza del ruido de salida RTx,k+1 suministrado al sistema, permite concluir que los tiempos involucrados tienen una independencia funcional, lo que hace que el filtro de Kalman sea una alternativa viable para reconstruir los tiempos de transporte.
3.3. Reconstrucción de los tiempos de transporte
El filtro de Kalman es un procedimiento matemático que opera por medio de un mecanismo de predicción y corrección (Ver Figura 14). El algoritmo predice el nuevo estado a partir de su estimación previa añadiendo un término de corrección proporcional al error de predicción, donde este es minimizado estadísticamente.
Entonces para la reconstrucción de los tiempos de transporte medidos se usará la versión escalar del filtro de Kalman, debido a que se tienen dos vectores de medición que corresponden a los tiempos de transporte de transmisión de información τTx,k y a los tiempos de transporte de recepción de información τTx,k , cuyo volumen de datos es muy extenso y afecta al desempeño de la reconstrucción elevando de manera exponencial su tiempo de cálculo. Entonces tomando en consideración a [22], las ecuaciones mostradas en (5, 6) se reescriben quedando de la siguiente manera en (14, 15) respectivamente:
donde xk es el estado interno del
sistema, a es el parámetro del sistema, b es
el coeficiente de la entrada del sistema, u es la entrada al
sistema, vk es el ruido asociado a
la entrada del sistema, yk es la
salida del sistema que corresponderá a los tiempos de transporte medidos,
c es el coeficiente del estado interno del sistema y
wk es el ruido asociado a la
salida del sistema. La predicción del estado interno del sistema
donde
Siendo Kk la ganancia K de Kalman y está definida en (18) por:
De tal manera que jk+1 es:
donde Qk es la covarianza del ruido asociado a la entrada del sistema, la cual es definida en (20):
Cabe aclarar que Pk+1 que se define como la varianza del error de identificación y está dada en (21):
donde Rk+1 es la covarianza del ruido asociado a la salida del sistema, el cual está dado por (22):
a. Reconstrucción de los tiempos de transmisión τTx,k y recepción τRx,k usando el filtro de Kalman
Al asegurar la independencia lineal de los ruidos asociados al sistema de entrada QTx,k y QRx,k así como de los ruidos asociados a la salida del sistema RTx,k+1 y RRx,k+1 es posible usar (18) para obtener la ganancia de Kalman que permitirá la reconstrucción de los tiempos de transmisión τTx,k . y de recepción τRx,k . El resultado de la ganancia de Kalman KTx,k y KRx,k a lo largo de la evolución del sistema se puede observar en la Figura 15 (línea negra y línea roja respectivamente).
De la reconstrucción de los tiempos de transmisión τTx,k y de los tiempos de recepción τRx,k través del uso del filtro de Kalman, se observó que los resultados obtenidos son muy próximos a los tiempos medidos en todos los valores de k, pero se considera que este argumento no es suficiente, lo que motiva el uso del error cuadrático medio para validarlo.
Para el caso del error cuadrático medio entre los tiempos de transmisión de información reales y reconstruidos se puede describir la convergencia del filtro mediante el empleo de (23, 24) hasta encontrar el mínimo error de HTx,k .
Entonces en la Figura 16 (línea azul) y de acuerdo a (24), el filtro de Kalman tiene una convergencia en casi todos los puntos, pues el error cuadrático medio HTx,k converge a valores muy pequeños: 0.0102 Segundos, para los tiempos de transmisión de información τTx,k , lo que permite describir la calidad de la reconstrucción pues a medida que se obtengan valores cada vez más pequeños de HTx,k durante el proceso de reconstrucción usando el filtrado de Kalman, la diferencia descrita por la ecuación (24) converge a valores cercanos a 0 (Ver Figura 16), lo que permite establecer que la dinámica de los tiempos de transmisión reconstruidos es similar a la de los tiempos de transmisión medidos, con lo que se valida la reconstrucción lograda a través del algoritmo.
Para el caso del error cuadrático medio entre los tiempos de recepción de información reales y reconstruidos se puede describiendo la convergencia del filtro mediante el empleo de (25, 26) hasta encontrar el mínimo error de HRx,k .
Por lo tanto en la Figura 16 (línea roja) y de acuerdo a la ecuación (26), el filtro de Kalman tiene una convergencia en casi todos los puntos, pues el error cuadrático medio HRx,k converge a valores muy pequeños: 0.011 Segundos, para los tiempos de recepción de información τRx,k , lo que permite describir la calidad de la reconstrucción pues a medida que se obtengan valores cada vez más pequeños de HRx,k durante el proceso de reconstrucción usando el filtrado de Kalman, la diferencia descrita por la ecuación (26), converge a valores cercanos a 0, lo que permite establecer que la dinámica de los tiempos de recepción reconstruidos es similar a la de los tiempos de recepción medidos, con lo que se valida la reconstrucción lograda a través del algoritmo.
b. Obtención del tiempo de transporte τk del sistema de telecontrol en tiempo real
Para el tiempo de transporte τk se usará la
definición 2 mostrada en este trabajo dada por (13). Entonces, para el tiempo de
transporte medido τk , se sumarán los tiempos de
transmisión τTx,k y recepción
τRx,k (reales y reconstruidos). En ambos
casos, se observó que los tiempos de transporte τk
obtenidos a partir de la medición, son muy próximos a los tiempos de transporte
reconstruidos
Para el primer momento de probabilidad de los tiempos de transporte medidos
El comportamiento del segundo momento de probabilidad de los tiempos medidos
Para validar los resultados mostrados, se usará el error cuadrático medio, definido a partir del error obtenido de (27, 28):
En la Figura 16 (línea negra) se puede
observar la gráfica que muestra el comportamiento de esta medida descriptiva. En
ella se ve que la reconstrucción del tiempo de transporte
Para los tiempos de transporte τk , lo que permite describir la calidad de la reconstrucción pues a medida que se obtengan valores cada vez más pequeños de Hτk durante el proceso de reconstrucción, la diferencia descrita por la ecuación (28), converge a valores cercanos a 0, lo que permite establecer que la dinámica de los tiempos de transmisión reconstruidos es similar a la de los tiempos de transmisión medidos, con lo que se valida la reconstrucción lograda a través del algoritmo computacional.
c. Tiempo de telecontrol TTc,k en tiempo real
Tomando en consideración la Figura 1, el tiempo de telecontrol TTc,k en un sistema de telecontrol en tiempo real, se considera como la suma algebraica del tiempo de ejecución ck y el tiempo de transporte τk , se propone la siguiente definición para el tiempo de telecontrol TTc,k .
Definición 5 (Tiempo de telecontrol en tiempo Real).
El tiempo de telecontrol en tiempo real TTc,k ∈ R+, es la suma algebraica del tiempo de ejecución ck ∈ R+ y el tiempo de transporte τk ∈ R+ en el intervalo k ∈ Z+. De tal manera que:
Entonces con el fin de cuantificar el tiempo de telecontrol que existe en los sistemas de control basados en esquemas de comunicación cliente - servidor se tomó en consideración a (29) y así determinar tiempo de telecontrol TTc,k que existe en los sistemas de tiempo real y que llegan a afectar el comportamiento del sistema controlado.
En el caso del tiempo de telecontrol medido se incluye la suma de los tiempos de transmisión τTxk , los tiempos de recepción τRx,k los cuales forman a los tiempos de transporte τk y los tiempos de ejecución ck .
Para el resultado de la suma algebraica de los tiempos obtenidos a partir de las
reconstrucciones presentadas en este trabajo. Cabe señalar que para los tiempos
de transmisión
En ambos casos, se observó que los tiempos de telecontrol
Para el primer momento de probabilidad de los tiempos de telecontrol medidos
Para el caso del comportamiento del segundo momento de probabilidad de los
tiempos de telecontrol medidos
Para asegurar esto, se usará el error cuadrático medio denotado por (30, 31):
En la Figura 16 (línea verde), se puede
observar que la reconstrucción del tiempo de telecontrol
4. Conclusiones
Un sistema de telecontrol en tiempo real es una forma de control de sistemas en donde se considera que los tiempos de comunicación existentes así como los tiempos de ejecución de las tareas o acciones de los sistemas participantes (sistema controlado y sistema controlador), influyen en la respuesta de ambos sistemas, provocando un efecto no deseado en el sistema controlado.
El hecho de medir los tiempos involucrados en el proceso de telecontrol permite conocer su dinámica de comportamiento mediante el empleo de medidas descriptivas, tal y como el primer y segundo momento de probabilidad, de lo cual se concluye que los tiempos de ejecución tienen una dinámica totalmente diferente a la de los tiempos de transporte. Por esa razón se utilizan para su reconstrucción métodos diferentes.
Para los tiempos de ejecución, se observó que al ser un proceso estocástico
estacionario en sentido débil, permitió el uso del método de la variable
instrumental y del filtrado digital difuso como estimadores del parámetro
Para el caso de los tiempos de transporte, el comportamiento de la dinámica de los tiempos de transmisión y recepción del sistema telecontrolado, se observó que son de tipo no estacionario, debido a que el primer momento de probabilidad no permanece constante conforme va evolucionando el sistema. Cabe mencionar que, para la reconstrucción de estos tiempos, se trató de usar tanto el Método de Variable Instrumental y el Filtro Digital Difuso como primeras opciones, pero no se obtuvieron resultados satisfactorios, debido a la naturaleza estocástica de los tiempos de comunicación. Por esa razón se propuso usar el filtrado de Kalman para la reconstrucción de los tiempos de transmisión y recepción involucrados en el proceso de telecontrol de sistemas en tiempo real por Internet.
De las reconstrucciones obtenidas para los tiempos de transmisión y recepción, se verificó que el error cuadrático medio obtenido a partir de su análisis, sea muy aproximado a las mediciones reales. Para la obtención del tiempo de telecontrol, se observó que esta forma de análisis en forma separada, determinará los límites de las restricciones temporales de los sistemas de telecontrol en tiempo real, tal y como el tiempo de ejecución ck , el plazo dk y los tiempos de respuesta tardíos rk existentes en el procesamiento, así como en la comunicación de sistemas de control.
En este sentido, la contribución principal del artículo fue proponer una metodología de reconstrucción de tiempos (ejecución, transmisión y recepción) en un sistema de telecontrol en tiempo real por internet, basándose en la medición, caracterización estadística por momentos de probabilidad.
Que en comparación con [2], el modelo reportado sirve para representar a los tiempos de codificación y compresión (identificado como el tiempo de ejecución en nuestro trabajo) así como el tiempo de transmisión, pero no toma en consideración el tiempo de recepción debido al alcance del modelo. Mientras que en comparación con [3], aunque el modelo reportado fue desarrollado bajo el esquema cliente - servidor sirve para modelar a los tiempos transmisión y recepción utilizando el protocolo de comunicación BlueZ (para la tecnología inalámbrica de comunicación Bluetooth 2.0) pero no fue desarrollado para el protocolo TCP.
En [4, 5] al realizar un análisis de modelos existentes concluyen que se han usado modelos en donde no se toma en consideración la variabilidad de los tiempos involucrados. Lo cual en este trabajo fue considerado y fue motivo para usar el Método de la Variable Instrumental, Filtrado digital difuso y el filtro de Kalman con buenos resultados.











 nova página do texto(beta)
nova página do texto(beta)














