1. Introduction

The energy conversion process in a typical crystalline solar cell occurs due to the absorption of photons that excites the valence and conduction bands of the semiconductor material, generating charge carriers to create electron-hole pairs, therefore a photocurrent is generated and collected by metallic contacts allocated in the top surface of the solar cell. A common geometric arrangement of the metallic contacts in rectangular solar cells is the H-pattern with finger-like contacts. The width of these contacts generates a small series resistance, for a wider electrode, the coverage of the solar cell is restricted, limiting the light transmission through to the semiconductor material junction (^{Reinders et al. 2017}). One of the major focus needed to understand the mechanism that increases the performance of solar cells is the reduction of the resistive power losses of the arrangement for the front metallic contacts. Moreover, different loss mechanisms are associated to the grid metallic contacts as grid resistance, shadowing due to grid reflection, emission of layer resistance and contact resistance between the metal contact and the semiconductor junction (^{Wen et al., 2010}). The process of collection between optically transparent and conductive materials, is limited since electrical carriers invariably scatter photons.

The H-pattern of metallic contacts in rectangular solar cells, inherently has a series of restrictions for the total collection, electrically inserting a series of contacts in parallel, connected with two busbars at right angles, implies the appearance of small losses that result in the efficiency, that is increased by assembling an array of cells of the collecting network to form a photovoltaic module (^{Reinders et al., 2017}). On the other hand, in a solar cell with circular geometry, generated by cutting thin layers of semiconductor material, the pattern of metallic contacts is composed of circular concentric (fingers) and radial contacts (busbars), where the main weakness was that not takes advantage of the total collection area (^{Patel, 2005}). In both geometries, a key factor is to maximize the electrical conductance and minimize the blockage of light. In this manner, the shape and structure are subjects of design the allocation of metallic material to reduce the shading losses and the associate resistive losses (^{Aiken & Barnett, 1999}). The influence of the metal grid pattern, linear and square, the resistive losses are less sensitive to illumination for the square grid than the linear arrangement, also, the resistive losses of the square grid are less influenced by the metal grid resistivity (^{Morvillo et al., 2009}).

In this manner, the geometric arrangement of the top metallic contact network in a solar cell can be designed for optimal coverage and collection of the photogenerated electrical current, for solar cells with increasing conversion efficiency capacity (^{Müller et al., 2020}). Conventional approaches of simple metallization patterns, such as the H-pattern, a cross-hatched pattern or a full metallization have been studied for square geometries (^{Burgers, 1999}; ^{Wen et al., 2010}). The grid design in a solar cell with circular geometry, generally used in concentration applications, considers a radial and concentric arrangement of metallic contacts (^{Bendib et al., 2012}; ^{Bissels et al., 2011}). Both approaches consider the loss mechanisms related to the grid as shadowing losses, top layer resistance towards the fingers, contact resistance at the fingers, and metal resistance in fingers and busbars. Recently, a conceptual design based on nature-inspired fractal structures has been proposed in flexible electrodes for solar cells (^{James & Contractor, 2018}), where the engineering design provides an optimal surface coverage and enhances the collection of electrical energy in optoelectronic devices (^{Han et al., 2014}).

On the other hand, constructal law allow us to design, predict and enhance the performance of physical systems, to generate evolutionary architectures in systems with imposed currents that flow through the physical system (^{Bejan & Lorente, 2008}). This methodology has proved to describe and predict vascular networks in functionalized vascular structures as the human liver or in cell matrix growth (^{Lorente et al., 2020}; ^{Sauer et al., 2021}), thermal energy storage systems (^{Malley-Ernewein & Lorente, 2020}), where the internal tree-shaped structures improve the transport of currents that flow through the system. The evolution of these structures in human and non-human made systems, depends to the degree of freedom to generate and adapt the flow architectures to persist in time with an improved performance (^{Lorente & Bejan, 2019}). In this sense, the constructal law design provides the methods to predict, design and develops evolutionary structures generating vascularized systems (^{Wang et al., 2007}). These structures are determined by the reduction of the resistance to flow subject to local restrictions to satisfy a main objective (^{Bejan, 2000}) and were developed mainly for reticular structures of high conductivity material inserts for cooling an adiabatic volume with an internal heat source (^{Bejan, 1997a}), flow structures in a porous volume (^{Bejan, 1997b}), defining aspect ratios of the inserts or tubes constructions, width ratios between inserts branches and surface covering in order to efficient the heat transfer or flow rate over a volume. he constructal law design has been considered also in solar cells and energy applications (^{Morega & Bejan, 2005}; ^{Ojeda et al., 2020}).

In parallel, a tree-shaped pipe network in a disc-shaped body was designed for the optimal fluid flow between a point and multiple points in the perimeter (^{Wechsatol et al., 2002}) and the geometric characteristics as the length of the branched pipes and angles of bifurcation were defined as a minimization of the flow resistance. The main feature of the optimized networks, which are defined by the constructal law design methodology, is the allometric relationships between characteristic lengths of the physical system as a function of physical and geometrical variables (^{Miguel, 2015}). An application of the tree-shaped networks for cooling a volume was reported by ^{Rocha et al. (2002)}, where the lengths and angles of ramification allow the compaction of the system. A common feature of the design process is to define and minimize the quantity of conductive material with coverage of the area. A generalized methodology for the optimal branching design of networks for fluid flow and heat transfer was developed by ^{Miguel (2018)}.

Also, the constructal law design methodology developed for the cooling of a volume with a heat generation source with a reticular pattern of high conductivity inserts (^{Bejan, 1997a}; ^{Ledezma et al., 1997}), has been applied for the design of the grid of metallic contacts in circuits and solar cells. The resulting geometric arrangement follows an H-pattern network of contacts with constant cross-section (^{Morega & Bejan, 2005}), a tree-like pattern (^{Ojeda et al., 2020}), and optimal variable cross-section (^{Chen et al., 2010}) in a rectangular solar cell. The main results are the optimal size of the constructal elements, number of branches, and length of the metallic contact. Such a process considers the minimization of the maximum voltage in order to get the minimum electrical resistance in every element of construction. This last characteristic is not necessarily desirable in the design process of a network projected to collect the electric current generated in a solar cell. On the other hand, in the collecting process of the generation of electric current in a solar cell due to solar radiation exposure, various mechanisms of optical and electrical losses are presented. The design of the network from the minimization of the resistive power losses from the overall voltage of the constructal element then defines the optimal length of the contact in every level of branching (^{Bhakta & Bandyopadhyay, 2005}).

As a common assumption in the constructal design process applied to electrical cases, it is convenient to consider that the electrical conductivity σ or resistivity ρ are constants. For this purpose, a vein power tree with optimal cross-sectional branches was designed based on constructal theory, in an elliptical circuit board for optimal distribution of direct current performance (^{Huang, Guo & Chu, 2011}). In this case, the optimal distribution of the electrical resistance is a key factor to determine a structure with minimal resistance. A similar case for a hierarchical concentric contact network is defined in a circular circuit board where the voltage is defined in a circular sector (^{Huang et al., 2011}). The optimal length, number of circular sectors, optimal resistance and voltage, were defined as a function of physical and geometrical parameters.

In this last work, a tree-shaped network for a disc with a heat generation source was defined by the constructal law method for cooling volumes with inserts of high thermal conductivity. The optimal number of sectors and angles of ramification is a consequence of minimizing the thermal resistance for two levels of branching, as was illustrated by ^{Rocha et al. (2002)}. Also, for the electrical case, a tree-shaped network on a disc-shaped circuit board is defined under the assumption of a fixed area. The metallic contact network connects the center to multiple points to the periphery, increasing the compaction for printed circuit boards for power distribution, geometry factors as the ratio of the widths is considered as a design parameter that defines the optimal length and aspect ratios for the circular sectors (^{Huang, Guo & Ye, 2011}).

In the present work, a theoretical study of the geometric design of the top metallic contact network is developed over a disc-shaped body solar cell, applying the constructal design methodology for the minimization of the resistive power losses. The optimal geometric characteristics of the contact network over the solar cell as the number of sectors, angles of branching, disc size, and lengths, are expressed in terms of the allocation of the metallic material, physical and geometrical parameters, which will be defined later in dimensionless variables.

2. Elemental circular sector

It is well known that the efficiency of a single solar cell is defined by the physical and chemical structure of the solar cell and metallic contact material, which defines the characteristics of the voltage of the equivalent electrical circuit. The electrical potential is assumed as not constant, due to the resistance of the solar cell material of the elemental circular sector, the electrical current flow causes a potential drop to occur, this causes a resistive power loss and consequently a decrease of the efficiency of the solar cell. Therefore, it is essential that in the interaction between the metallic contact network and the surface of the solar cell material, implicitly related to the different geometric characteristics in order to minimize the resistive power losses due to the current flow in the solar cell and metallic contact region.

As a first step in the optimization process is necessary to define an elementary system where the main physical and geometrical variables are considered. A solar cell with a disc-shaped body, is also composed of a circular sector of radius R and constant thickness w .

The elemental circular sector is operated with a uniform rate for the electric current density J in A/m² with increments of temperature that are not significant enough compared to the global temperature of the solar cell, therefore the solar cell is considered to operate isothermally (^{Raga & Fabregat-Santiago, 2013}), with no mechanical or thermal stresses. The properties of the solar cell and metallic contact material are considered constants. The boundaries of the constructal element are considered without electrical leaks.

As a first approximation of the application of the constructal design, the resistance losses due to the rear contact surface and optical shading are not considered. However, the coverage due to the allocation of the metallic material of the contact is analyzed by a dimensionless parameter ϕ , which will be defined later. The first optimization corresponds to a semi-circular sector with a metallic contact, that connects the periphery to the center in a radial pattern, with length and width L₀ and D₀, respectively. Once optimized this elemental system, the optimal length, the total number of sectors are defined. In this case, we assume that the length L₀ is equal to the radius R of the semi-circular sector, later the optimal length of the metal contact will be defined. We anticipate that successive constructions, with a branched contact arrangement, the disc radius is defined as a function of the length projections of the branched contacts.

The elemental circular sector is considered to have a slender geometry, H0≪R, with an angle α and known area A₀. The area can be approximated as an isosceles triangle A₀≈ H₀R/2 . We anticipate that this approximation will be helpful to define the total area of the branched elements based on the area A₀, disc-size, and number of sectors distributed over the disc-shaped body solar cell. The first element and coordinate system are shown in Figure 1.

Figure 1 First element of construction. 

In transverse direction y , a solar material cell is allocated and has a constant value the electrical resistivity ρ_s. At the center of the element, is placed a metallic insert of width D₀, thickness δ , and a constant value of the resistivity ρ_m, that collects photogenerated electrical current by the solar cell material. The electrical resistivity of the metallic material ρ_m is considered smaller with respect to electrical resistivity ρ_s of the solar cell material.

3. First construction level

A branched metallic contact is allocated in the solar cell with a disc-shaped body of radius R . The first construction level considers n -slender building blocks with a known area, A₁ ≈ H₁L₁/2. The geometric arrangement of the metallic contacts in a semi-circular sector of angle α for a single solar cell with a disc-shaped body over which appear two bifurcations delimited by the angle β . The geometric array of branched contacts is composed of a geometrical optimized central sector of radius L₀ and n -branched contacts of width D₁ in a peripheral circular sector of radius L₁. The n -branched contacts collect the photogenerated electrical current in the solar cell material and transport it to the central metallic contact to one point to confluence in a semi-circular sector.

The optimal lengths of the top metallic contacts and the aspect ratio of the semi-circular sector of radius R of the branched array helps to define the number of sectors of angle 𝛼 distributed along the circumference of a disc-shaped solar cell. A sketch of the branched array of top metallic contacts is shown in Figure 2.

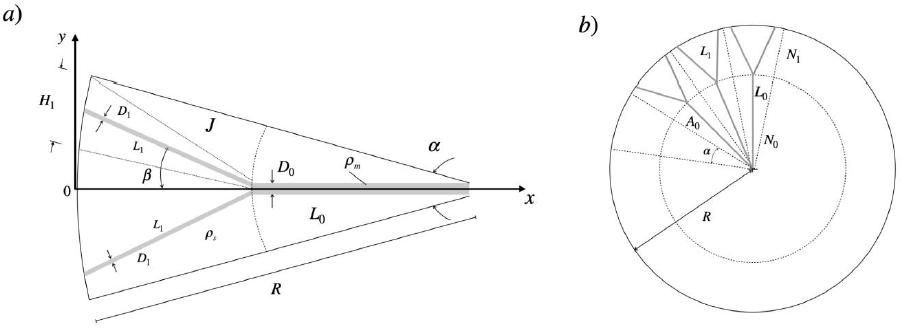
Figure 2 a) Semi-circular sector with a bifurcated top metallic contact. b) Sketch of the distribution of sector of angle α in a single solar cell with a disc-shaped body. 

As a part of the optimization process, an aspect ratio H-1 opt is defined applying the constructal methodology to peripheral sectors of area A₁, shown in the previous section. The result of the aspect ratio and power loss are similar to the central sector of length L₀, given by Eq.(15) as a function of physical and geometrical parameters. With the aid of these results, the optimal length L₁ and the power loss of the peripheral sector can be defined. The optimal aspect ratio and minimum power loss of the first construction is given by;

The geometric characteristics of the branched arrangement over the disc-shaped body solar cell, such as the angle α , are defined with the aid of the definition of the number of peripheral sectors N₁ That is α = 2πn/N1 determines the distribution of the branched metallic contacts and is given by the following relationship:

where R-=R/A112 is a dimensionless radius.

The aspect ratio of the central sector of length L₀ can be defined considering that the angle α is approximated as α≅H0/L0, with the aid of Eq.(21) and considering that L0≅R-L1, an expression of the area A₀ is defined as a function of the geometric characteristics of the branched arrangement. This result helps us later to define the area ratio A₀/A₁, the area A₀ is defined by the following expression;

To define the power loss of the central sector of radius L₀ where occurs the electric current confluence from the branched contacts is necessary to define the aspect ratio H-0. The electrical collection can be defined from a charge conservation at x=L₀, where the electric current collected by the metallic n -contacts converge to the contact of the central area of area A₀. Assuming that Kirchoff´s law is fulfilled and carrying out a current balance at the convergence point, the collected electric current can be defined as a boundary condition with the following expression.

Following the methodology described in section 2.1, the power loss of the central sector is defined and consequently, an aspect ratio H-0 considering the collection due to the n-contacts. Expressing the power loss in dimensionless terms of the area A₁ the aspect ratio can be defined by;

Where A₀/A₁, is defined by Eq.(22).

The total power loss of the geometrical arrangement can be easily expressed by adding Eq.(20) to the power loss of the central sector. The resulting expression defines the contribution of the inserts of length L₁ and the electrical current collection of the central sector with the n -contributions of electrical current. This is given by the following expression;

where the term (A₀/A₁)²(ϕ₀/ϕ₁)² can be defined with the aid of the Eq.22) as a function of ϕ₁ and the width ratio D,- defined below.

The occupied area of the metallic contacts in an n -branched arrangement over the circular sector, help us to define the total allocation of the 𝑛-branched arrangement of metallic contacts. The occupied area A_p1 is given by A_p1= ND₁L₁+ (N/n)D₀L₀, from this definition, and the lengths L₀ and L₁, area ratio Φ =A_p1/A₁ is defined as:

where D-=D0/D1 is a width ratio of the metallic contacts.

On the other hand, a single solar cell can be modeled as an equivalent circuit with a current generator as a photogeneration system, where the recombination current mechanism is represented by a diode and a series and shunt resistances. The series resistance represents the bulk resistance of the semiconductor, contacts and interconnection. The shunt resistance considers the leakage of electrical current around the edges of the solar cell. This series resistance is desirable to be minimal to improve the collection of electric current generated by the semiconductor material. Minimizing this series resistance improves the fill factor, this is a parameter that evaluates the quality of the current-voltage process, defined with the equivalent circuit of a solar cell (^{Lee, 2010}).

The electric resistance due to the geometric arrangement of the top metallic contacts over the disc-shaped solar cell can be considered as a bulk contact resistance between the semiconductor and metallic contacts that contributes to the resistive power losses over the solar cell, as a first approximation. The branched arrangement defined by the constructal design method can be considered as series resistance (radial contact) and parallel resistances (branched contacts) and expressed as an equivalent series resistance over the semi-circular sector.

From Eq.(7), we can define the equivalent dimensionless electric resistance of the geometrical arrangement of top metallic contacts, applying the constructal design method (^{Huang et al., 2011}; ^{Huang, Guo & Ye, 2011}; ^{Huang, Guo & Chu, 2011}; ^{Morega & Bejan, 2005}; ^{Ojeda et al., 2020}). This electrical resistance is defined by evaluating the voltage drop of the constructal element at the point where the voltage drop in vertical and horizontal directions is maximum. The expression of the dimensionless resistance, Δψ = (V_m+ V₀)δ/JAρ_m is defined with the aid of the areas definition A₀, A₁ and the optimal aspect ratios H-0, H-1, defined previously in section 2 and 3. The dimensionless resistance of the assembly in a semi-circular sector is given by the following expression;

where optimal aspect ratios H-0,H-1, are defined by Eqs.(20) and (24), respectively. These geometric features are defined by the minimization of the resistive power losses and substituted in Eq.(27) in order to analyze the influence of the allocation of the arrangement of metallic contacts.

4. Results

The total power losses for the geometric arrangement of metallic contacts with respect to geometrical characteristics, defined by Eq.(25) are shown in Figures 3 and 4 for the bifurcated case, n = 2 The value of the dimensionless parameters as resistivity´s ratio ρ- and thickness ratio w- are defined with the reported data from metallic contact and common solar cell characteristic materials (^{Benick et al., 2017}; ^{Deng et al., 2016}; ^{Richter et al., 2017}). In the following figures, we fixed the values Φ=0.001, w-=0.4,ρ-=5.3x10-5, and R-=2.

Figure 3 Total resistive power losses for the bifurcated arrangement of contacts. 

Figure 4 Total power loss and geometrical characteristics versus R- for n=2 

Figures 3a) and b) show the minimum values of P-tot with respect to the geometrical parameter ϕ₁ for different values of branching angle β . In Figure 3a), for an angle β = 10 degrees, the resistive power loss presents a minimum value of P-tot≅418 at ϕ1≅0.00059, approximately. As the angle β increases, the power loss is also increased, shifting the power distribution curves to the left of Figure 3a). In Figure 3b), for a value of β = 60 degrees, a minimum value of P-tot is presented at ϕ1≅0.00056. On other hand, for a right angle (β = 60 degrees), in Fig. 3b) the minimum value of the power loss P-tot occurs at a smaller value of ϕ1≅0.00054 with respect to the value that corresponds to a small branching angle. As the value of the β angle increases, the minimum value of the power loss occurs at a lower value of ϕ₁, that is, the amount of metallic material of the contact decreases.

In order to analyze the influence of the disc size, given by R-, on the main characteristics of the bifurcated metallic contacts arrangement, we take fixed the value of ϕ1 opt≅0.00059 for an angle β = 0 degrees, where a minimum value of P-tot is presented. With this value of ϕ_{1 opt} an optimal configuration of the metallic contacts network is defined, due to that ϕ₁ indicates how the metallic material of the contact is allocated over the circular constructal element. In Figure 4, keeping fixed the values of the dimensionless parameters used previously, the dimensionless power loss and geometric characteristics of the branched arrangement as the number of sectors, width ratio and dimensionless length with respect to R- are shown.

The resistive power loss presents a double minimum value for two geometric parameters, associated with the presence of the metallic material, ϕ₁ and the disc size R-. As shown above, the first is presented at the value of the geometrical parameter ϕ1≅0.00059, the second minimum value P-tot≈418 corresponds to a value of R-opt≈2. For values of R->2 the power losses tend to increase. On other hand, the optimal width ratio D-opt is defined with the aid of Eq.(26) as a function of the number of branches n and the geometric parameters ϕ₁ and Φ. As R- increases, the width ratio D-opt tends to a constant value approximately of D-opt≈1.6, this value indicates that D₁< D₀, the width of the branched contacts are reduced with respect to the central contact of the semicircular sector. The influence of the number of branched contacts 𝑛 on the width ratio D- is shown below.

The optimal length of the metallic contact of the central sector, in a branched arrangement, L-0 opt≈R--L1/A11/2 , is independent of the number of branched contacts n , and increases as R- increases. The length L-0 opt tends to a null value approximately at R-≈1.65 when the geometric parameter ϕ_{1 opt}= ϕ₀, this value corresponds to the case of a radial pattern when the value of ϕ₀ takes the value of ϕ₁. On the other hand, the number of sectors tends to a value N_{1 opt}≈ 50 as the disc size is increased. If the number of sectors increases in the disc-shaped body solar cell, the angle α , given by Eq.(21), tends to decrease.

In the following Figures 5 and 6, the influence of the number n of branched contacts is shown, for a fixed value of β = 10 degrees and maintaining the same values of the dimensionless parameters ρ-, w- used previously. The power losses for an n -branched arrangement present a minimum value with respect to the allocation of the metallic contact, given by ϕ₁. As the number n of branches increases, the minimum value of the power losses increases, due to the presence of branched metallic contacts and occurs at a lower value of the geometric parameter ϕ₁.

Figure 5 Total resistive power losses versus ϕ₁ for n branched contacts. 

Figure 6 a) Total resistive power losses and b) optimal width ratio for n branched values. 

Meanwhile, in Figure 6, we use the corresponding optimal value of the geometrical parameter ϕ_{1 opt} where the minimum power loss is presented, for every n -branched value given in Figure 5, to reveal the influence on the power losses of the 𝑛-branched contact arrangement and the width ratio D-opt with respect the disc size R.-

In Figure 6a) the total power losses present a minimum values for an n -branched arrangement of the metallic contacts, for the bifurcated case, n = 2 , the minimum is presented at R-≈2.0 in comparison to n = 8 where the minimum value of the power loss is presented at R-≈1.89. The minimum value of the power losses for the branched case is less than the geometric arrangement with eight branches i.e. P-tot n=2< P-tot n=8. For a value of n > 2 , the minimum value of the power losses occurs at a lower value of the disc size, given by R.-

In Figure 6b) we show the corresponding width ratio D-opt as a function of R-. The optimal width ratio increases and tend to a value as the dimensionless radius R- increases. For the case of n = 2 , the width ratio tends asymptotically to a value of D-opt≈1.6. For n = 8 , D-opt tends to D-opt≈6.8. As the number of branches of the metallic contact increases, the optimal width ratio D-opt tends asymptotically to higher values i.e. D1≪D0, as the dimensionless radius R- increases.

The minimum total power losses P-tot min of the geometrical arrangement with respect to the entire disc area is shown in Figure 7. The previous results were obtained with total power losses, given by Eq.(25). For this purpose, we rewrite Eq.(25) in terms of the area of the disc A = πR² in order to describe the behavior of the power loss with respect to the disc size, considering the optimal value of ϕ_{1 opt} for every 𝑛-value of branching and a fixed value ϕ₀=0.0001 for the radial pattern. As the disc size increases, the total power loss of the branched arrangement tends to decrease asymptotically to a value close to P-tot min≈2.5.

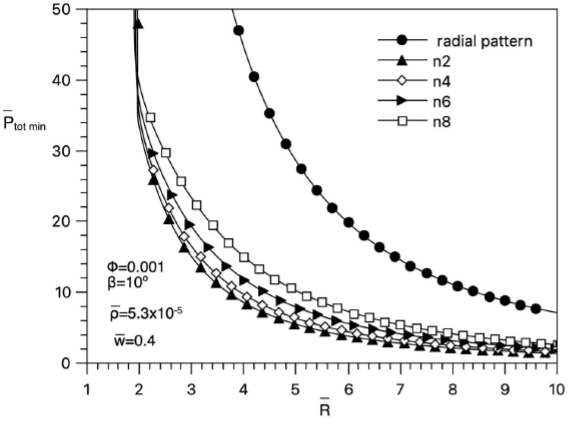
Figure 7 Total power losses of the geometric configuration of the metallic contacts for n branched values. 

For a value of R- approximately of 1.96, the power loss of the branched arrangement has a divergent behavior and for smaller values of this critical value of R-, there is no solution for the power loss. The power loss for a radial pattern of the metallic contacts, given by Eq.(16) presents higher values and asymptotic behavior, the power loss tends to P-tot min≈7.0. Otherwise, for values of R- larger than this critical value, the power loss presents always the smallest values. The bifurcated case given by n = 2 compared with higher values of branching, presents an asymptotic value close to P-tot min≈1.38. For a geometric arrangement of n = 8 the power loss reaches asymptotically a value close to 2.6 as the disc size increases. The minimum values of resistive losses are presented for the bifurcated case.

The number N₁ of peripheral sectors of area A₁, defined with the aid of the expression of the angle α , given by Eq.(21), tends to increase when the size of the disc is also increased. For the bifurcated case at R-=4, the number of peripheral sectors is N1≈21, for a higher value of R-=10 the corresponding value is N1≈52. As the number of peripheral sectors N₁ is proportional to R-, the number of sectors for every 𝑛 value of branches of the metallic contact is similar to each other as the disc size R- increases.

Finally, the equivalent dimensionless electric resistance of the metallic contacts arrangement, given by Eq.(27), is a function of the optimal aspect ratios of the constructal semi-circular sectors, defined by the minimization of the resistive losses are a function of the number n of branches, geometrical and physical parameters, mainly.

We have fixed the same values of the parameters used in the previous Figure 7, in order to show the equivalent resistance of an arrangement of series and n -parallel resistances. The dimensionless equivalent resistance is shown in Figure 8.

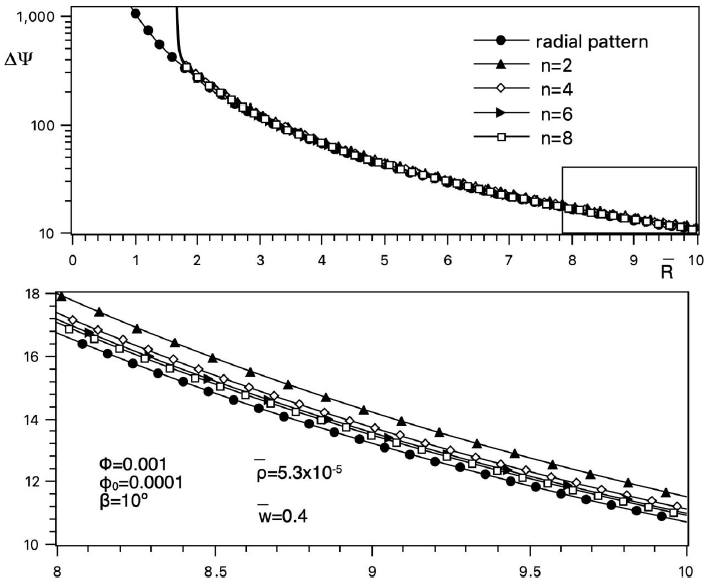
Figure 8 Dimensionless resistance of the constructal assembly of metallic contacts for n branched values. 

The dimensionless electric resistance Δψ presents a divergent value at R-≈1.6 due to the definition of the aspect ratio H-0 opt of the central sector of a branched configuration. For large values of R-, the dimensionless resistance presents an asymptotic behavior and tends to a value close to Δψ ≈11.0 . For values n > 2 , the dimensionless electric resistance presents the lowest values compared to the bifurcated case but increases the resistive losses. The equivalent resistance of the geometric arrangement of the contacts can be considered as a series resistance. This resistance is desirable to be minimal to improve the collection of electrical current generated.

The main objective of the present work is to define the geometric arrangement of metallic contacts over a disc-shaped solar cell by the reduction of the associated resistive losses. The bifurcated arrangement of contacts presents the reduced value of resistive losses and consequently an equivalent electrical resistance with which can help to calculate the parameters to evaluate the global efficiency of the arrangement, generally conceptualized as an equivalent electric circuit, presented by a current generator, diode, series resistances that represent the bulk resistance of the semiconductor and contacts materials, shunt resistances that represent the leakage of electrical current.

5. Conclusions

The constructal design method allows designing a tree-shaped metallic contact network by the minimization of the power loss. The main parameters that allow us to define this geometry are the allocation of the metallic contact in shape optimized constructal elements, electrical resistivity´s ratio ρ- and the area ratio between the branched metallic contacts and disc-shaped solar cell, given by Eq.(26). As a consequence, we can define the optimal lengths of the metallic contacts with the aid of the optimal aspect ratios of the central and branched constructal elements. Also, with the optimal lengths, we can define the minimum overall resistance of a branched arrangement considered as a series and shunt resistances arrangement applying the constructal methodology reported by ^{Ojeda et al. (2020)}. On the other hand, it is well-known that the main factors that influencing efficiency, are the structure of the semiconductor material of the solar cell, anti-reflection coatings, the series resistance of the metallic contacts, and the effect of shadowing due to the contacts, among others. The losses related to the metallic contact grid, influence directly the conversion efficiency of solar cells (^{Wen et al., 2010}). A common feature of the constructal design method is the ratio between the surface area of the network and the total area of the studied geometry and is used to determine the influence of the pipe diameter ratio, for the fluid transport network (^{Miguel, 2015}; ^{Wechsatol et al., 2002}), or the width ratio of metallic inserts, for thermal case (^{Bejan, 1997a}; ^{Rocha et al., 2002}). For the solar cell case, this geometrical characteristic is the same to define the shadowing effect as a ratio of the surface area of the fingers in the unit cell and the total solar cell area (^{Bissels et al., 2011}). Thus, this characteristic is considered in the total power loss of the n-branched arrangement, given by Eq. (25). To evaluate the efficiency is necessary to define the solar cell material, the series and shunt resistances of the constructal top metallic network and consider the specific maximum current density corresponding to the maximum power point of performance. For further work, is necessary to evaluate experimentally the performance of the tree-like metallic contact network in a solar cell with a disc-shaped body under laboratory conditions and field experiments, evaluate the geometrical characteristics, compare and redesign the shape and structure of the contact network.