1. Introduction
In many engineering and physical applications, the Duffing oscillator is one of the most important models. It used in electric circuit, oscillation of plasma, optical stability and the buckled beam as illustrated by Siewe et al. (2006) and Trueba et al. (2004). Huang (2018) used nonlinear time delayed feedback controller to restrain the vibrations of Van der Pol oscillator and investigated the efficacy of the feedback gain on bifurcation point. Numerically, Barron (2016) clarified the behavior of the stable and unstable response of the ring of coupled Van der Pol oscillators. Barron crystallized that, if the stability conditions are not satisfied, the amplitude of Van der Pol oscillator increased. Kumar et al. (2016, 2017, 2018), modulated and illustrated the bifurcation analysis of Van der Pol - Duffing - Rayleigh oscillator. Amer et al. (2020a), used two different time delays one for position and the other for velocity to restrain the vibrations of the Van der Pol - Duffing - Rayleigh oscillator. They found that the vibrations were reduced by about 94% from its value without control and the effectiveness of the time delay controller Ea is nearly about 17. Kamel (2009) researched and simulated coupled Van der Pol oscillators exited by multi forces. He investigated the stability of this system at two primary resonances using frequency response equations. Using negative acceleration feedback control, Sayed et al. (2018) controlled the vibrations of the Van der Pol oscillator caused by harmonic and parametric forces. Wang et al. (2018), offered a tuned damper (passive control) to rein the vibrations of Van der Pol oscillator. The positive position feedback (PPF) controllers with time delay were used for suppressing the vibrations of coupled Van der Pol oscillators by EL-Sayed (2020). He demonstrated the effectiveness of the PPF controllers with time delay and it was as follows, Ea equal 198.92 for y1 and equal 227.02 fory2. Amer et al. (2020b), studied the stability of the Van der Pol - Duffing - Rayleigh oscillator which is presented by one-degree-of- freedom containing the cubic nonlinear terms and an external force in the presence of the nonlinear integral positive position feedback controller. The averaging method was used to obtain the approximate solution of many nonlinear dynamical systems by Yang et al. (2010), Yuan et al. (2012) and Sinha (1997). Hamed et al. (2020), used the nonlinear proportional derivative controller (NPD) to suppress the vibrations of a vertical conveyor system. The amplitudes of two modes decreasing about 95.33% and 82.45% from its values before using the NPD control. Amer et al. (2020b) studied the numerical and stability of a Hybrid Rayleigh-Van der Pol-Duffing Oscillator controlled with NIPPF. He, C. H. et al studied the Stability analysis and controller. Sadeghi et al. (2021). studied Particle Swarm Optimization (PSO) By increasing the number of terms in the trial functions that have been selected, the error can be further reduced. In addition, among the known analytical approaches, IAGM is the most user- friendly and easy. Then, in order to find the unknown coefficients of the trial function, an optimization technique (in this case, PSO) is used to minimize the DE's residual, with the boundary/initial conditions being the second objective to be reduced. As a result, the problem was usually multi-objective in nature, and it was solved using the weighted-sum decomposition method.
In this work, we studied the behavior and stability of the Van der Pol - Duffing - Rayleigh oscillator equation which presented by Kumar et al. (2018). The averaging method was introduced to obtain the solvability conditions of vibrating system. We applied the PD controller to suppress the vibrations of the main system at the primary resonance case. MATLAB program was used to demonstrate the efficacy of various parameters and the PD gains.
2. Mathematical Modelling
Kumar et al. (2018) presented the equation of motion of a Hybrid Rayleigh-Van der Pol-Duffing oscillator by one- degree-of-freedom as:
If we applied an external force to the Hybrid Rayleigh-Van der Pol-Duffing oscillator as shown in figure 1 and applied the proportional derivative controller to suppress the vibration caused by this force. The equation (1) can be written as in this circumstance.
With the initial conditions u(0) = 0,
Table 1 List of symbols.
| u,u̇,ü | Displacement, velocity and acceleration of main system respectively. |
| µ | The damping coefficients of main system. |
| ω | The natural frequency of main system. |
| F | External excitation force amplitude frequency of external force. |
| Ƞ,β,δ,θ,k, and λ | Nonlinear coefficients of the main system. |
| α1 | The proportional gain of control signal. |
| α2 | The differential gain of control. |
| ε | Small perturbation parameter |
2.1. The averaging method
According to Nayfeh (1985), to use the averaging method firstly, we will use the variation of the parameters method to change the dependent variable u to the two dependent variables. The amplitude and phase of the free oscillation term. To do this, we observe that, the general solution of equation (2) is
where, a and φ are constants Differential equation (3) with respect to t then:
The solution of equation (2) still on the form shown in equation (3) subject to the constrain shown in equation (4) but a, φ be time varying. Once again, we will differentiate equation (3) with respect to t
By comparing equations (4) and (5) we have the following equation,
Again, we will differentiate equation (4) with respect to t
Now substituting from Eqns. (3), (4) into Eq. (2) to obtain the following equation:
From Eqns. (7) and (8), we can write the following equation:
2.2. Periodic Solution
In this part, we introduced the detuning parameter𝜎to examine the stability of the system at the primary resonance case as the following:
Inserting equation (10) into equation (9) then we obtain:
where, Φ = σt - φ. We will apply the standard averaging method in interval [0, 2π]. Multiplying equation (6) by cos(ωt + φ) and (11) by sin(ωt + φ) adding the results, and noting that cos2(ωt + φ) sin2(ωt + φ), we obtain
where,
After evaluating all integrals in equations (12) and (13), we got the following:
3. Fixed point solution
The steady-state solution happens when,
Squaring then adding equations (16) and (17) to get the following response equation
3.1. Non-linear solution
While in movement to evolve the steady state solution's stability, start with the following procedures:
where, a0 and Φ0 are the solutions of equations (16) and (17). The perturbations a1 and Φ1 are very small comparing with a0 and Φ0 so, after substituting from equation (19) into equations (14) and (15) we keep only the linear terms of a0 and Φ0. From this procedure, we get the following system:
For the above system's solution to be stable, the real part of its eigenvalues must be negative.
4. Numerical Consequence
To scrutinize the results of the system numerically, we used "Ode 45" package in MATLAB program. Also, we investigate the stability of the hybrid Rayleigh-Van der Pol-Duffing oscillator using the averaging method and the influence of different parameters on the behavior of controlled system was illustrated. We introduced a comparison between the approximate solution which obtained from the average method and the numerical one. We used the following parameters values
4.1. Time History
The behavior of the hybrid Rayleigh-Van der Pol-Duffing oscillator was studied at primary resonance case before and after using PD controller. Figs. 2a and 2b, exhibit the time histories of the main system for the open and closed loop cases. The sold red line shows the numerical integration solutions of the main system while the dotted blue one shows the averaging solutions. From the figures, the amplitude of controlled system was reduced about 95% from uncontrolled system. This means that the performance of the control Ea is about 21. The agreement of numerical solutions using RK-4 method to approximate solutions using averaging method was illustrated also in these figures. From Figs. 3a and 3b, we can determine the suitable values of the proportional gain α1 and the differential gain α2 which were selected as α1 = 4.4 and α2 = 5.
4.2. Response curves
In this subsection, we scrutinized the frequency response curves and the effect of the proportional gain α1, the differential gain α2 the excitation force f and the damping coefficient μ. Graphically, we presented the steady-state amplitude versus the detuning parameter σ using equation (18). From Figure 4a, the main system will be destroyed by increasing the external force. So, we used PD controller to suppress vibrations of the main system as shown in Figure 4b. From this figure, we write down that the frequency response curve presented by one peak drown by black line. The outcomes of applying RK-4 presented by red circles. There is a good agreement between two results. In figure 5a, we used three various values of the proportional gain α1. The response curves are shifted to right or to left established on the values of proportional gain α1 which means that the assignment of the PD controller is to modulate the system natural frequency ω. Figure 5b shows the frequency response curves of the main system at different values of the differential gain α2. PD-controller term appends more damping to the main system amplitude. So, the amplitude of controlled system decreases as the differential gain α2 increases. Moreover, the jump phenomenon and multi-valued solutions vanished. Despite of the effectiveness of the PD-controller in reducing the vibrations of the mine system, the maximum of the main system amplitude occurs at σ ≈ 0. We used the suitable values of the proportional gain α1 and the differential gain α2 from figure 3 (α1 = 4.4 and α2 = 5.0) to study the effectiveness of the external force and damping coefficient. Figs 5c and 5d show that the amplitude is monotonic increasing function to the external excitation force and monotonic decreasing function to the damping coefficient.
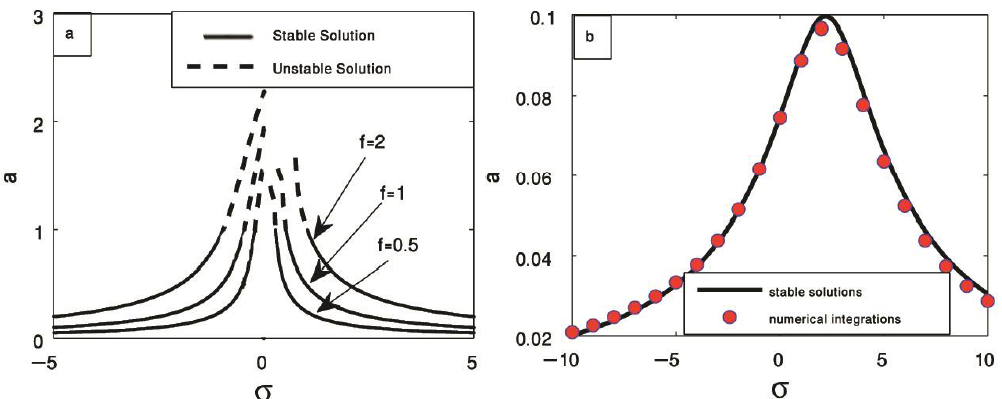
Figure 4 Influence of the external force without controller and (b) the response curve after controller.
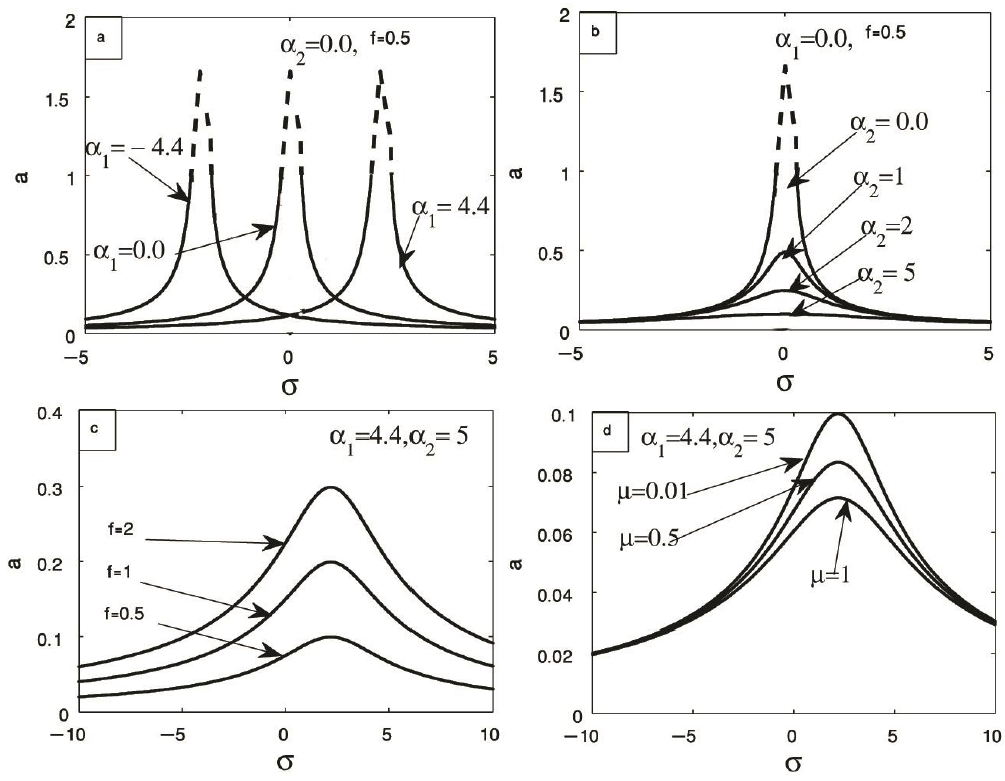
Figure 5 The response curves for (a) different values of the proportional gain α1, (b) different values of the differential gain α2, (c) different values of the excitation force and (d) different values of the damping coefficient.
In figures 6 and 7, we presented the gains-response curves for different levels of the excitation force. Figure 6 shows that, for positive and negative values of the proportional gain α1 (for negative and positive position feedback), decreasing the amplitude of the main system. By increasing the positive gain α2 (negative velocity feedback), decreasing the main system amplitude with high rates. For negative differential gain α2 (positive velocity feedback), the system exhibits unstable response as shown in Figure 7. Figures 8 and 9 show the time histories corresponding to points A and B on figures 6 and 7. From these two figures, we can see that, the high agreement between the response curves and the time histories.
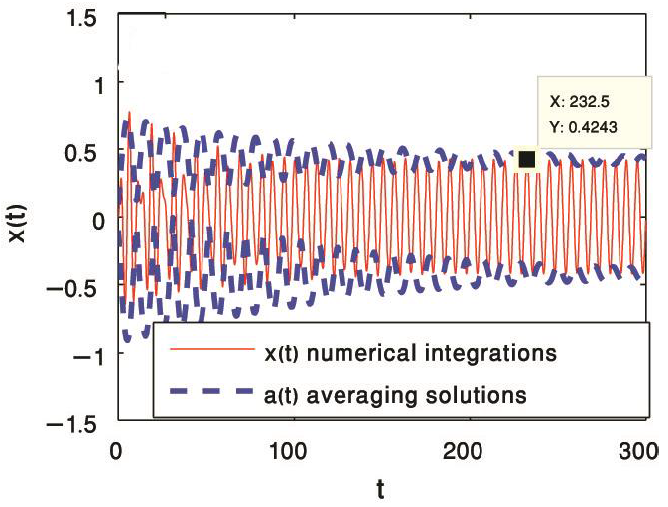
Figure 8 The time histories of the main system for f = 0.5 and σ = 0 corresponding to the point A on Fig. 6.
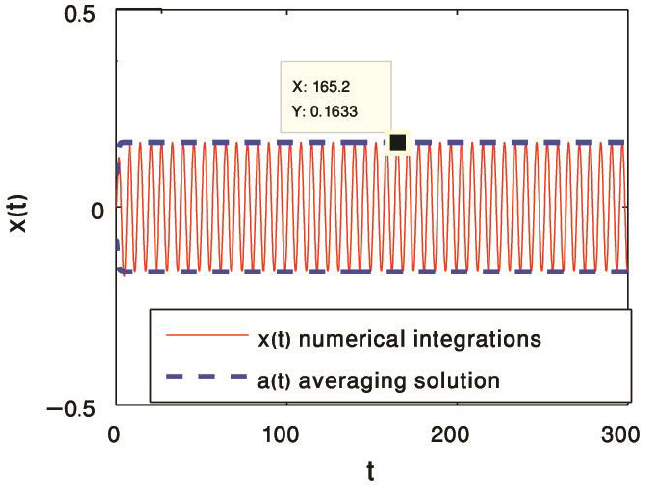
Figure 9 The time histories of the main system for f = 0.5 and σ = 0 corresponding to the point B on Fig. 7.
5. Conclusions
In many engineering and physical applications, the Duffing oscillator is one of the most important models. It used in electric circuit, oscillation of plasma, optical stability and the buckled beam. The vibrations analysis and dynamic responses of a Hybrid Rayleigh Van der Pol- Duffing oscillator subjected to external excitation force were investigated. For obtaining the approximate solution of the vibrating system, we applied the average method. We used PD controller to suppress the vibrations of a Hybrid Rayleigh-Van der Pol- Duffing oscillator, the amplitude of controlled system was reduced about 95% from uncontrolled system. This means that the performance of the control Ea is about 21. From this study, we can note some important results for the influence of the vibrating system's parameter such that.
The behavior of the controlled system increased with increasing the external excitation force f.
The behavior of the controlled system decreased with increasing the damping coefficient.
The response curves are shifted to right or to left established on the values of proportional gain.
P-controller is to modulate the system natural frequency.
The amplitude of controlled system decreases as the differential gain increases.
D-controller term appends more damping to the main system amplitude.
There is a conformity of FRC solutions with RK-4 solutions.











 nova página do texto(beta)
nova página do texto(beta)







