Introducción
La protección marginal contra la erosión en ríos es una componente esencial y costosa en los sistemas de protección contra inundaciones. Entre las más comunes se encuentran los recubrimientos, diques marginales y espigones; el objetivo de estas obras es redireccionar el flujo de tal manera que se evite el contacto entre el flujo con alta velocidad y el material que conforma las márgenes del cauce (Nguyen, Vo, & Gourbesville, 2018; Qin, Zhong, Wu, & Wu, 2017; Sukhodolov, 2014). En el caso particular de los espigones, son estructuras colocadas dentro del cauce, colocadas de manera perpendicular o bien con cierto ángulo de inclinación respecto a la margen. Su propósito es redirigir y alejar las líneas de corriente que inciden en la margen, evitando así problemas de erosión y arrastre de material. Existen estudios que reportan el funcionamiento hidráulico de los espigones, desde simulaciones numéricas (Mawandha, Wignyosukarto, & Jayadi, 2018; McCoy, Constantinescu, & Weber, 2007a; McCoy, Constantinescu, & Weber, 2008) hasta estudios de laboratorio (Kang, Yeo, Kim, & Ji, 2011; Weitbrecht, Socolofsky, & Jirka, 2008; Zhang et al., 2017). En su mayoría, estos trabajos se limitan a estudiar espigones que emergen de la superficie libre del agua y están colocados de forma perpendicular a la margen; siendo los espigones sumergidos y los orientados a un cierto ángulo con la orilla los menos estudiados (McCoy, McCoy, Constantinescu, & Weber, 2007b; Jiménez-León, Mendiola-Lizárraga, Rivera-Trejo, Nungaray-Núñez, & Díaz-Arcos, 2017). Hoy día, un sinnúmero de estas estructuras se han construido usando sólo el buen juicio y la experiencia del constructor en lugar de seguir alguna norma o criterio específico (Minor, Rennie, & Townsend, 2007). En México, como en muchos países de Latinoamérica, la principal referencia en la que se basan la mayoría de los diseños de protecciones marginales es el Manual de ingeniería de ríos, elaborado por el Instituto de Ingeniería de la Universidad Nacional Autónoma de México (UNAM) (Maza-Alvarez, García-Flores, & Olvera-Salgado, 1996); sin embargo, dado que cada corriente natural presenta condiciones hidráulicas que la hacen única, prevalece la necesidad de estudiar el dimensionamiento, espaciamiento y orientación óptima de espigones para cada caso en particular. En este trabajo se simuló numéricamente en HEC-RAS (Brunner, 2016) un arreglo de siete espigones orientados con cierto ángulo respecto a la margen, y que tienen una parte sumergida y otra que emerge del cauce. En su diseño se siguió la metodología propuesta por Maza-Alvarez, García-Flores y Olvera-Salgado (1996), y su funcionamiento hidráulico fue analizado por medio de un modelo físico reducido. El análisis en modelos físicos es costoso y, salvo algunas excepciones, lo más común es hacer simulación numérica. Sin embargo, la simulación numérica no es tarea sencilla e involucra experiencia no sólo en el análisis e interpretación de los resultados, sino también en la manera de introducir los datos y proponer las condiciones de frontera. Debido a que en la modelación numérica no existe una regla sobre la forma de modelar geométricamente los espigones, en este trabajo se probaron tres alternativas: 1) como una barrera; 2) como un conjunto de obstrucciones escalonadas, y 3) como terreno natural. Se encontró que los perfiles hidráulicos generados por las tres opciones de espigón presentaban un comportamiento similar al medido en el modelo físico reducido. Por lo tanto, se decidió modelar el espigón como una barrera debido a que su ingreso al modelo requiere menos tiempo y esfuerzo. Por último, a partir de simulaciones numéricas se analizaron alternativas que tuvieran el mismo funcionamiento hidráulico del arreglo propuesto de siete espigones, pero que redujeran de modo sustancial el número de los mismos. Los resultados obtenidos fueron una protección marginal con base en recubrimiento y cuatro espigones.
Por su parte, los modelos computacionales desarrollados para estudiar el comportamiento hidráulico de un cauce o un diseño en particular varían por la complejidad de su algoritmo computacional, su grado de sofisticación y confiabilidad. Los distintos modelos se definen como modelos de una (1D), dos (2D) o tres (3D) dimensiones. Los modelos 1D consideran que la componente principal del perfil de velocidades es a lo largo del eje de coordenadas x; por lo tanto, a diferencia de los modelos bidimensionales (2D) y tridimensionales (3D), se desprecian las componentes de velocidad en los ejes de coordenadas y y z. Estos modelos consideran la elevación promedio de la superficie de agua en la dirección y y z; son de gran popularidad, pues son menos exigentes computacionalmente (Rau-Lavado, 2007), y requieren menor cantidad de información para compilar que los modelos 2D y 3D. Estas características les han dado un uso extendido por encima de modelos más complejos. Ejemplos de modelos 1D son: HEC-RAS (Brunner, 2016), Mike11 (DHI, 2016) e Iber (Bladé et al., 2014), entre otros. En este trabajo se empleó el software HEC-RAS, el cual es un programa de acceso libre, desarrollado y actualizado de forma constante por el Centro de Ingeniería Hidrológica del Cuerpo de Ingenieros de EUA. Presenta un entorno intuitivo, por lo que los datos son fáciles de editar, modificar y visualizar en pantalla. Aunque HEC-RAS tiene la posibilidad de considerar transporte de sedimentos, no se usó debido a que el modelo físico no lo reproducía. HEC-RAS es un programa validado en Norteamérica, México, y muchos países de Latinoamérica y el mundo. En México es requerido por dependencias gubernamentales del ámbito federal, estatal y municipal para realizar la modelación hidráulica de cauces abiertos, ríos y canales artificiales.
Materiales y métodos
Caso de estudio
Con la intención de proteger a la ciudad de Villahermosa, Tabasco, contra inundaciones (Rivera-Trejo, Soto-Cortés, & Barajas-Fernández, 2009), en el año 2010 se propuso construir una serie de canales derivadores sobre los principales ríos que escurren hacia la ciudad. El objetivo fue disminuir el caudal de estos ríos y reducir el riesgo de desbordamiento e inundación en la ciudad ubicada aguas debajo de los mismos. Los canales derivadores son aberturas que se realizan en los ríos con el objetivo de desviar parte de su caudal hacia otro lugar. En el caso de Villahermosa, los canales derivadores dirigen el flujo hacia zonas de regulación natural. Para maximizar el caudal derivado, estas obras por lo general se ponen en curvas de ríos. Esto deja a las márgenes susceptibles a la erosión, por lo que deben protegerse.
El caso analizado considera una protección marginal ubicada aguas abajo del canal derivador Sabanillas, localizado en el municipio de Centro, Villahermosa, Tabasco, coordenadas 512627 E, 1979777 N. La protección consiste en un arreglo de siete espigones de roca tal y como se muestra en la Figura 1.
Modelo físico reducido
Con la finalidad de determinar el funcionamiento hidráulico de la estructura derivadora, se construyó un modelo físico reducido Esc 1:40 (Figura 2). En el modelo se midieron de forma experimental: a) los niveles de agua sobre la curva y el canal; b) el caudal derivado.

Figura 2 Prototipo y modelo físico de la estructura derivadora Sabanillas, municipio de Centro, Villahermosa, Tabasco.
El modelo físico se instrumentó con medidores dinámicos de nivel distribuidos a lo largo de la curva del río y el canal (Figura 3a). El caudal derivado (Figura 3b) fue medido por medio de vertedores triangulares; mientras que las velocidades en el canal se midieron con una micropropela de baja velocidad (Figura 3c). La topografía fue calibrada con el auxilio de un perfilador topográfico marca Wallingford, con una tolerancia de 0.001 m (Figura 3d). La instrumentación del modelo físico y la calidad de los datos permitieron lograr una buena calibración del modelo numérico.

Figura 3 Medición de niveles: a) detalle del medidor de nivel; b) detalle de canal derivador; c) microprolela de baja velocidad; d) perfilador topográfico.
En el modelo experimental se estudiaron: a) los efectos que tendría un solo espigón ubicado sobre la margen derecha del río donde termina el canal derivador; b) el arreglo de siete espigones distribuidos a lo largo de la margen derecha. Ambos experimentos fueron simulados numéricamente y los valores medidos se usaron con fines de calibración del modelo.
Modelación numérica
El primer paso en la simulación numérica fue determinar la forma de ingresar la geometría de los espigones al modelo. Esto debido a que es posible hacerlo de varias maneras y cada una de ellas difiere en el grado de complejidad. Los elementos físicos y las variables geométricas que se emplean para caracterizar a los espigones se muestran en la Figura 4.
Donde Xe es la separación entre espigones; B, el ancho del río; R, radio de curvatura; LT, longitud de trabajo; k, talud; ϕ, ángulo de orientación, y β es ángulo de expansión.
Se consideraron tres alternativas para el análisis. La primera consideró ingresar la geometría del espigón como una barrera (Figura 5a). La longitud fue la equivalente a la longitud de trabajo más la mitad de la longitud de la punta del espigón; la altura se definió como la elevación al final de la longitud de trabajo más la mitad de la altura de la longitud de trabajo. La segunda consideró al espigón como un conjunto de obstrucciones escalonadas (Figura 5b), con una obstrucción inicial en el fondo y obstrucciones escalonadas alrededor de la primera. El ancho de cresta propuesto originalmente en los espigones, fue el equivalente a la longitud de trabajo, y la altura se definió como la elevación al final de la longitud de trabajo más la mitad de la altura. El resto de las obstrucciones fueron distribuidas de tal manera que cubrieran la superficie del espigón original. La tercera opción fue modelar al espigón como parte del terreno natural (Figura 5c). Se modificó la configuración topográfica del terreno y se generó un modelo digital del terreno (MDT). La construcción del MDT se llevó a cabo a partir de datos topográficos recolectados en campo.
Calibración
El modelo numérico fue calibrado con los caudales de entrada y salida medidos en el modelo físico, el caudal derivado y los niveles de la superficie libre del agua medidos en seis puntos de sondeo h 0-h 6 (Figura 6). Se varió el coeficiente de rugosidad hasta que los resultados de la modelación numérica reprodujeran de forma aceptable los resultados medidos de manera experimental en el modelo físico.
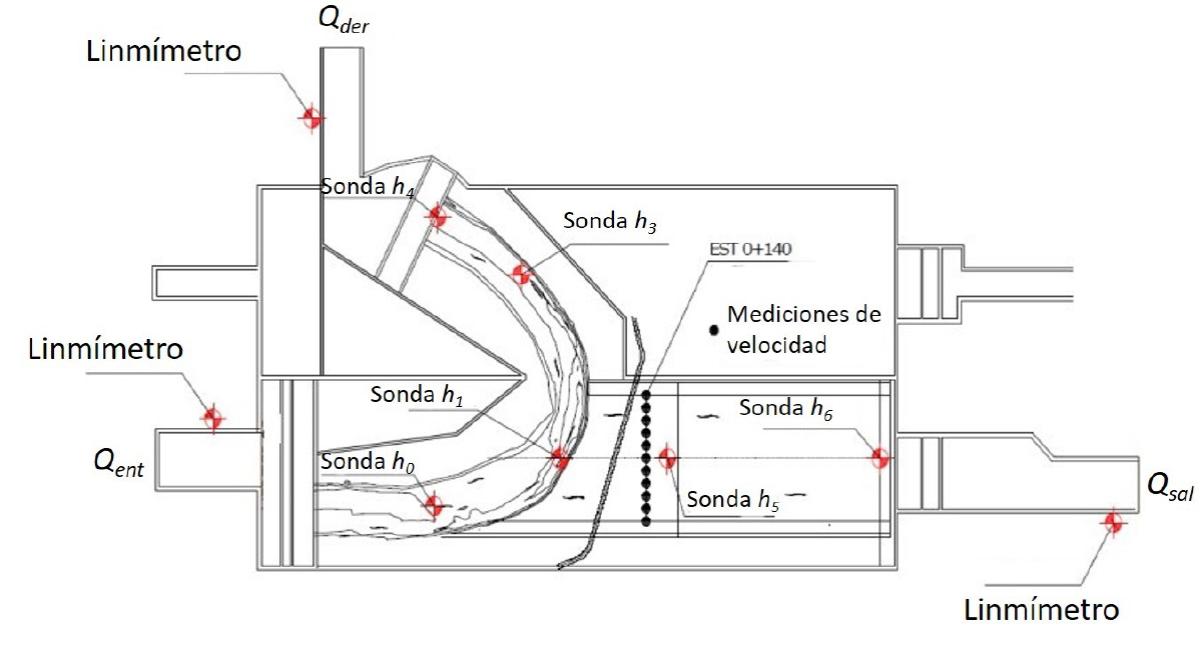
Figura 6. Variables monitoreadas en el modelo físico reducido: Q ent, caudal de entrada; Q sal, caudal de salida; Q der, caudal derivado; h 0-h 6, ubicación de medidores dinámicos de nivel.
Una vez calibrado el modelo, se analizaron las diferencias de los niveles de la superficie libre del agua medido experimentalmente contra los simulados con las opciones de geometría propuestas (barrera, escalones y terreno natural); así como el perfil hidráulico resultante.
Elegida la manera óptima de ingresar la geometría de los espigones, se procedió a ingresar el arreglo de los siete espigones (Figura 7), y se comparó su funcionamiento medido de modo experimental contra el simulado de forma numérica.
Propuesta alterna al arreglo de espigones
Además, a la comprobación de la simulación numérica del arreglo de espigones, se decidió aplicar el modelo numérico con fines de diseño. Por lo tanto, se revisaron los criterios de diseño de espigones considerados en el Manual de ingeniería de ríos (Maza-Alvarez et al., 1996), en cuanto a: el ángulo de expansión y de orientación, la separación entre espigones y la longitud de trabajo de los mismos, etcétera. El objetivo fue evaluar la posibilidad de algún otro tipo obra de protección, que tuviera el mismo efecto, pero pudiera reducir el volumen de obra. Las opciones propuestas fueron: a) la colocación de un recubrimiento marginal (Figura 8a), y b) combinación de recubrimiento marginal, con un arreglo menor de espigones (Figura 8b). Ambas alternativas se modelaron en HEC-RAS y se obtuvieron los perfiles hidráulicos, al igual que las curvas de funcionamiento del canal derivador.
Resultados
Modelación en condiciones naturales
En la Tabla 1 se muestran los valores de la n de Manning propuestos, los resultados numéricos obtenidos y el valor medido de forma experimental, y que reproduce las condiciones naturales.
Tabla 1 Calibraciónde coeficiente de rugosidad de Manning.
| Coeficiente de rugosidad n | Gasto m3/s | LA (msnm) |
|---|---|---|
| 0.025 | 1 305 | 6.63 |
| 0.024 | 1 357 | 6.61 |
| 0.023 | 1 417 | 6.61 |
| 0.023 y 0.0226 en la última estación aguas abajo | 1 438 | 6.59 |
| Medición en modelo físico | 1 450 | 6.60 |
Por lo tanto, en la curva se empleó el coeficiente de Manning (n) de 0.023 y en la sección aguas abajo 0.0226. Además, debido a que tanto la curva como el canal de derivación fueron construidos con el mismo material, en el canal también se empleó un coeficiente de Manning de 0.023.
Modelación numérica del tipo de geometría de los espigones
Se compararon los perfiles hidráulicos medidos en el modelo físico contra las simulaciones numéricas con las distintas maneras de ingresar la geometría de los espigones. En la Tabla 2 se muestran los niveles medidos experimentalmente y los generados a partir de la modelación numérica en los puntos de sondeo en la curva del río (h 0, h 3 y h 4) y el canal derivador (h 1, h 5 y h 6). En la simulación se consideraron las tres opciones de geometría del espigón: a) barrera, b) conjunto de obstrucciones escalonadas (escalones), y c) terreno natural (TN). El rango de los caudales analizados fue desde el momento en que el canal empieza a derivar (1 000 m3/s) hasta el caudal de desbordamiento (1 600 m3/s).
Tabla 2 Niveles medidos en el modelo físico reducido y simulaciones numéricas.
| Q ent = 1 600 m3/s | |||||||
|---|---|---|---|---|---|---|---|
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.84 | 6.92 | 0.08 | 6.91 | 0.07 | 6.91 | 0.07 |
| 7.13 | 6.93 | 0.20 | 6.93 | 0.20 | 6.92 | 0.21 | |
| 6.96 | 6.91 | 0.05 | 6.91 | 0.05 | 6.91 | 0.05 | |
| Canal | 6.73 | 6.83 | 0.10 | 6.81 | 0.08 | 6.81 | 0.08 |
| 5.94 | 6.10 | 0.16 | 6.27 | 0.33 | 6.27 | 0.33 | |
| 3.38 | 3.05 | 0.33 | 3.05 | 0.33 | 3.05 | 0.33 | |
| Δh promedio = | 0.15 | 0.18 | 0.18 | ||||
| Q ent = 1 503 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.76 | 6.77 | 0.01 | 6.75 | 0.01 | 6.75 | 0.01 |
| 6.86 | 6.71 | 0.15 | 6.71 | 0.15 | 6.71 | 0.15 | |
| 6.74 | 6.69 | 0.05 | 6.69 | 0.05 | 6.69 | 0.05 | |
| Canal | 6.73 | 6.68 | 0.05 | 6.65 | 0.08 | 6.66 | 0.07 |
| 5.81 | 5.97 | 0.16 | 6.11 | 0.30 | 6.11 | 0.30 | |
| 3.69 | 2.93 | 0.76 | 2.93 | 0.76 | 2.93 | 0.76 | |
| Δh promedio = | 0.20 | 0.23 | 0.22 | ||||
| Q ent = 1 450 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.64 | 6.70 | 0.06 | 6.68 | 0.04 | 6.68 | 0.04 |
| 6.79 | 6.62 | 0.17 | 6.62 | 0.17 | 6.62 | 0.17 | |
| 6.57 | 6.60 | 0.03 | 6.60 | 0.03 | 6.60 | 0.03 | |
| Canal | 6.50 | 6.61 | 0.1 | 6.59 | 0.09 | 6.59 | 0.09 |
| 5.62 | 5.92 | 0.30 | 6.05 | 0.43 | 6.05 | 0.43 | |
| 2.61 | 2.89 | 0.28 | 2.89 | 0.28 | 2.89 | 0.28 | |
| Δh promedio = | 0.16 | 0.17 | 0.17 | ||||
| Q ent = 1 397 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.66 | 6.59 | 0.07 | 6.56 | 0.10 | 6. 7 | 0.09 |
| 6.62 | 6.47 | 0.15 | 6.47 | 0.15 | 6.47 | 0.15 | |
| 6.50 | 6.45 | 0.05 | 6.45 | 0.05 | 6.45 | 0.05 | |
| Canal | 6.57 | 6.50 | 0.07 | 6.47 | 0.10 | 6.48 | 0.09 |
| 5.54 | 5.85 | 0.31 | 5.97 | 0.43 | 5.97 | 0.43 | |
| 3.42 | 2.82 | 0.60 | 2.82 | 0.60 | 2.82 | 0.60 | |
| Δh promedio = | 0.21 | 0.24 | 0.24 | ||||
| Q ent = 1 307 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.57 | 6.48 | 0.09 | 6.45 | 0.12 | 6.46 | 0.11 |
| 6.48 | 6.32 | 0.16 | 6.32 | 0.16 | 6.32 | 0.16 | |
| 6.33 | 6.30 | 0.03 | 6.30 | 0.03 | 6.30 | 0.03 | |
| Canal | 6.4 | 6.4 | 0.00 | 6.37 | 0.03 | 6.37 | 0.03 |
| 5.53 | 5.75 | 0.22 | 5.84 | 0.31 | 5.84 | 0. 1 | |
| 3.31 | 2.73 | 0.58 | 2.73 | 0.58 | 2.73 | 0.58 | |
| Δh promedio = | 0.18 | 0.21 | 0.20 | ||||
| Q ent = 1 199 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.40 | 6.50 | 0.10 | 6.29 | 0.11 | 6.30 | 0.10 |
| 6.24 | 6.32 | 0.08 | 6.13 | 0.11 | 6.13 | 0.10 | |
| 6.10 | 6 30 | 0.20 | 6.10 | 0.00 | 6.10 | 0.00 | |
| Canal | 6.33 | 6.43 | 0.10 | 6.22 | 0.11 | 6.22 | 0.11 |
| 5.31 | 5.62 | 0.31 | 5.70 | 0.39 | 5.70 | 0.39 | |
| 3.13 | 2.62 | 0.51 | 2.62 | 0.51 | 2.62 | 0.51 | |
| Δh promedio = | 0.22 | 0.21 | 0.20 | ||||
| Q ent = 1 102 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.28 | 6.18 | 0.10 | 6.14 | 0.14 | 6.15 | 0.13 |
| 6.00 | 5.93 | 0.07 | 5.93 | 0.07 | 5.93 | 0.07 | |
| 5.96 | 5.90 | 0.06 | 5.90 | 0.06 | 5.90 | 0.06 | |
| Canal | 6.10 | 6.11 | 0.01 | 6.07 | 0.03 | 6.08 | 0.02 |
| 5.15 | 5.48 | 0.33 | 5.53 | 0.38 | 5.53 | 0.38 | |
| 3.04 | 2.51 | 0.53 | 2.51 | 0.53 | 2.51 | 0.20 | |
| Δh promedio = | 0.18 | 0.20 | 0.14 | ||||
| Q ent = 1 000 m3/s | |||||||
| Sondeo | Exp | Barrera | Δh (m) | Escalones | Δh (m) | TN | Δh (m) |
| Nivel (msnm) | |||||||
| Curva | 6.16 | 6.01 | 0.15 | 5.97 | 0.19 | 5.98 | 0.18 |
| 6.80 | 5.74 | 0.06 | 5.74 | 0.06 | 5.74 | 0.06 | |
| 5.68 | 5.70 | 0.02 | 5.70 | 0.02 | 5.70 | 0.02 | |
| Canal | 6.00 | 5 95 | 0.05 | 5.91 | 0.09 | 5.92 | 0.08 |
| 5.03 | 5.36 | 0.33 | 5.39 | 0.36 | 5.39 | 0.36 | |
| 2.87 | 2.41 | 0.46 | 2.41 | 0.46 | 2.41 | 0.46 | |
| Δh promedio = | 0.18 | 0.20 | 0.19 | ||||
Las diferencias promedio de elevaciones entre los datos medidos y los simulados fue de: ΣΔh Barrera = 0.18, ΣΔh escalones = 0.20 y ΣΔh TN = 0.19
Debido a que la menor variación se obtuvo modelando al espigón como barrera, se eligió este tipo de geometría con dimensiones de ancho, altura y longitud promedio. Esta opción requiere de un menor tiempo para ingresar su geometría al modelo numérico.
Modelación numérica del arreglo de los siete espigones
Una vez determinada la manera de ingresar la geometría de los espigones al modelo, el siguiente paso fue ingresar el arreglo de los siete espigones. Debido a que el efecto producido por el arreglo de espigones se refleja sobre todo en la curva del canal (punto de sondeo h 1), fue el que se tomó de referencia para comparar las mediciones experimentales contra las simulaciones numéricas. La Tabla 3 muestra los niveles medidos experimentalmente (Exp) y los generados a partir de la modelación numérica en HEC-RAS con el arreglo de siete espigones. En la columna Δh se muestra la diferencia de niveles entre ambos resultados y la Δh promedio.
Tabla 3 Resumen de niveles en la derivación con arreglo de siete espigones.
| Caudales | h deriv | Δh (m) | ||
|---|---|---|---|---|
| Q alimentación | Q derivación | Exp | HEC-RAS | |
| (m3/s) | (msnm) | |||
| 1 438 | 639 | 6.94 | 6.86 | 0.08 |
| 1 397 | 596 | 6.89 | 6.76 | 0.13 |
| 1 309 | 500 | 6.76 | 6.68 | 0.08 |
| 1 204 | 385 | 6.57 | 6.59 | 0.02 |
| 1 102 | 294 | 6.42 | 6.46 | 0.04 |
| 1 001 | 223 | 6.28 | 6.31 | 0.03 |
| Δh promedio = | 0.06 | |||
Se observó que la variación entre los resultados medidos y los simulados numéricamente fue en promedio de 0.06 m. Se consideró que este resultado es aceptable y, por lo tanto, el modelo numérico simulaba de forma adecuada el funcionamiento de la estructura derivadora. El siguiente paso fue modelar una alternativa que reprodujera el mismo efecto ocasionado por el arreglo de siete espigones, pero con volumen de obra menor.
Propuesta alterna al arreglo de siete espigones
Los resultados obtenidos con las propuestas consideradas fueron los siguientes:
Recubrimiento marginal. La Tabla 4 muestra los niveles medidos en la curva h 1 con arreglo de siete espigones (columna Exp), y los compara contra los obtenidos con el recubrimiento en HEC-RAS (columna RECUB). En la columna Δh se muestra la diferencia entre ambos resultados, así como el promedio de los mismos.
Tabla 4 Resumen de niveles en la derivación con recubrimiento.
| Caudales | h deriv | Δh(m) | ||
|---|---|---|---|---|
| Q alimentación | Q derivación | Exp | RECUB | |
| (m3/s) | (msnm) | |||
| 1 438 | 639 | 6.94 | 6.57 | 0.37 |
| 1 397 | 596 | 6.89 | 6.44 | 0.45 |
| 1 309 | 500 | 6.76 | 6.33 | 0.43 |
| 1 204 | 385 | 6.57 | 6.19 | 0.38 |
| 1 102 | 294 | 6.42 | 6.03 | 0.39 |
| 1 001 | 223 | 6.28 | 5.86 | 0.42 |
| Δh promedio = | 0.41 | |||
Se observó que la diferencia promedio en la lámina de agua entre ambas configuraciones fue de 0.41 m. Es decir, que con el recubrimiento marginal no se alcanza a reproducir de modo adecuado el efecto de derivación.
Recubrimiento más cuatro espigones. La Tabla 5 muestra los niveles medidos en la curva (h 1) con el arreglo de siete espigones (columna Exp), y los compara contra los obtenidos con la modelación numérica del recubrimiento y un arreglo de cuatro espigones propuesto (columna Rec + 4E). En la columna Δh se muestra la diferencia de nivel entre los resultados de las modelaciones numéricas y los resultados experimentales.
Tabla 5 Resumen de niveles en la derivación con recubrimiento y cuatro espigones.
| Caudales | h deriv | Δh | ||
|---|---|---|---|---|
| Qalimentación | Qderivación | Exp | Rec+4E | Rec+4E |
| m3/s | msnm | m | ||
| 1 438 | 639 | 6.94 | 6.81 | 0.13 |
| 1 397 | 596 | 6.89 | 6.70 | 0.19 |
| 1 309 | 500 | 6.76 | 6.62 | 0.14 |
| 1 204 | 385 | 6.57 | 6.52 | 0.05 |
| 1 102 | 294 | 6.42 | 6.39 | 0.03 |
| 1 001 | 223 | 6.28 | 6.24 | 0.04 |
| Δh promedio = | 0.10 | |||
Se observó que entre los resultados de las mediciones experimentales y de la modelación numérica de la alternativa propuesta, la variación promedio en la lámina de agua es de 0.10 m, y la variación entre los resultados obtenidos con la modelación de los siete espigones y la modelación del recubrimiento combinado con el arreglo de cuatro espigones es de 0.04 m. Se considera que esta variación no es significativa, por lo que esta alternativa puede reproducir de manera adecuada el efecto derivador.
Volumen de obra
Con fines comparativos, se muestra el concentrado de la estimación en volumen de obra que requiere cada alternativa (Tabla 6).
Tabla 6 Comparación de volúmenes de obra.
| Volumen original del proyecto (m3) | |
|---|---|
| Arreglo de siete espigones | 12 687.21 |
| Volumen de alternativa propuesta (m3) | |
| Recubrimiento | 4 948.16 |
| Arreglo de cuatro espigones | 6 024.28 |
| Total = | 10 972.44 |
| Diferencia = | 1 714.77 |
Se estimó una reducción en el volumen de obra de alrededor de 1 700 m3, lo cual, en términos económicos, representa un ahorro significativo.
Conclusiones
En las simulaciones numéricas se empleó el software HEC-RAS, modelo numérico hidráulico que puede trabar en 1D o 2D. El objetivo fue realizar el análisis hidráulico en una curva de un río, en la cual se hizo una derivación y se agregó una protección marginal con base en espigones. El fenómeno hidráulico es evidentemente tridimensional (3D), por lo que se piensa que el uso de un software 1D, podría considerarse limitado. Aquí se empleó HEC-RAS 1D y se contrastó su desempeño contra datos medidos experimentalmente en un modelo físico reducido, teniendo resultados aceptables. Se encontró que la mejor manera de modelar espigones en este caso fue como una barrera, pues además de que los resultados numéricos comparados contra los medios presentaron la menor diferencia (0.06 m), esta opción requiere un menor tiempo para ingresar la geometría al modelo numérico. También se llevó a cabo la modelación de una alternativa de protección, que consistió de un recubrimiento y cuatro espigones, encontrando que este arreglo reproduce el efecto generado por el arreglo original de siete espigones, pero con menor volumen de obra. Por último, en este estudio se empleó como parámetro de comparación y calibración la elevación de la lámina de agua, encontrando que HEC-RAS 1D presentó un buen desempeño para análisis hidráulicos de espigones en curvas. Sin embargo, se recomienda una vez realizado el análisis 1D y elegido el diseño final, emplear un análisis 2D, hacer un análisis de sensibilidad y contrastar estos resultados con los obtenidos en el modelo 1D.











 texto em
texto em 








