Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Agrociencia
versão On-line ISSN 2521-9766versão impressa ISSN 1405-3195
Agrociencia vol.50 no.8 Texcoco Nov./Dez. 2016
Crop science
Genetic erosion of the three-way line maize hybrid parents of a synthetic variety
1Fitotecnia. Universidad Autónoma Chapingo. 56230. Chapingo, Estado de México, México. (jsahagunc@yahoo.com.mx)
The advanced generations of three-way line maize (Zea maize L.) hybrids (THs) could be considered synthetic varieties (SVs) formed by random mating of their lines (Sin L). However, it was shown that there are differences depending on the type of hybrid and the inbreeding coefficient of the lines that form the hybrids (F), among other factors. To investigate the THs in this context, the loss of genes that are non-identical by descent (NIBD) was determined, which takes place during the formation of the sample of the m individuals that represent each one as parent of an SV. The hypothesis of the study was that genetic erosion does occur. The use of non-related lines was considered and that each one comprises a virtual population with 2-F NIBD genes. The average number of NIBD genes lost by a TH per sampling (GNIBDP) is expressed as 3(2-F) minus the number of NIBD genes that reach the sample. It was found that GNIBDP is inversely related with m and F. If F=1, in order for GNIBDP to be 0.15 or less, m must be equal to or greater than 4, or 15 or more when F=0. These numbers indicate that erosion should not occur with samples of several hundred, as occurs in seed production. When F>0 the imbalance of the gene frequencies of the lines in each TH should produce an inbreeding coefficient in the Sin t higher than that of Sin L.
Key words Genes; non-identical by descent; inbreeding coefficient; Zea mays L
Las generaciones avanzadas de híbridos trilineales (HTs) de maíz (Zea mays L.) podrían considerarse como variedades sintéticas (VSs) formadas por apareamiento aleatorio de sus líneas (Sin L), pero se ha mostrado que hay diferencias dependientes del tipo de híbrido y del coeficiente de endogamia de las líneas que forman los híbridos (F), entre otros factores. Para investigar a los HTs en este contexto se determinó la pérdida de genes no idénticos por descendencia (NIPD) que ocurre durante la formación de la muestra de los m individuos que representan a cada uno como progenitor de una VS. La hipótesis de estudio fue que sí ocurre erosión genética. Se consideró el uso de líneas no emparentadas y que cada una constituye una población virtual con 2-F genes NIPD. El número promedio de genes NIPD que pierde un HT por muestreo (GNIPDP) se expresó como 3(2-F) menos el número de genes NIPD que sí llegan a la muestra. Se encontró que GNIPDP se relaciona inversamente con m y F. Si F=1, para que GNIPDP sea 0.15 o menos, m debe ser igual o mayor a 4, o 15 o más cuando F=0. Estos números indican que no debe ocurrir erosión con muestras de varios centenares como ocurre en la producción de semilla. Cuando F >0 el desbalance de las frecuencias génicas de las líneas en cada HT debe producir un coeficiente de endogamia en el Sin t mayor al del Sin L.
Palabras clave: Genes no idénticos por descendencia; coeficiente de endogamia; Zea mays L
Introduction
In Mexico, the use of synthetic varieties (SVs) of maize (Zea mays L.) formed with pure high yield lines is not common, due to the scarcity of this type of parents (Espinosa et al., 2002; Luna et al., 2012) and the limited availability of inexpensive seed of outstanding single cross hybrids. Pérez-López et al.(2014) mention this as the reason for recurring to the production of three-way (THs) or double-cross hybrids, but they are seldom sown recurrently by the same farmer. Some farmers exploit their advanced generations instead of buying original seed again. The resulting populations could be considered like the SVs that would form with the parents of the cultivated hybrids, but this may not be the case (Márquez-Sánchez, 2010; Sahagún-Castellanos and Villanueva-Verduzco, 2012). Of the differences between these two types of populations, that due to the balanced participation of the genetic material of the lines in the SV that would be formed stands out, given that this does not occur when the parents are THs formed with the same lines, for example. In this case, each line of a single cross contributes half of the genetic material with respect to what is supplied by the third line of the three-way cross. This important difference is manifested in the inbreeding coefficient reported by Márquez-Sánchez (2010) for an SV formed with THs constructed with pure lines. The differences may also appear when there is genetic erosion. Escalante-González et al. (2013) consider that the randomness of the genetic mechanism, the finite number of individuals represented by each parent of an SV, and the heterozygous condition of its genotypes enable the loss of genes during its development. These authors studied the occurrence of genetic erosion during the formation of SVs whose parents are single crosses, and found that the loss of genes that are non-identical by descent (NIBD) is inversely related to the inbreeding coefficient of their parents. Furthermore, due to differences in the gene frequencies with which the lines participate in the SVs, there must be a loss of genes NIBD in different quantities among those formed only by lines and those generated by THs whose parents are the same lines, regardless of their inbreeding coefficient.
With respect to the formation of SVs from THs, the objective of the present investigation was to determine the magnitude of genetic erosion that would occur during the formation of the sample of individuals that represent each parent.
Materials and methods
The model of a locus in a diploid species reproduced by random mating was considered in this investigation. To this respect, it was assumed that the initial L lines with which the THs are formed are not related, that their inbreeding coefficient is F (0≤F≤1), and that L is a multiple of three. According to the characteristics of the lines, independently of the gene frequencies, it was assumed that each one of these contains 2 - F NIBD genes.
The number of NIBD genes that on the average are lost by a TH [(NIBD)pt] was expressed as the initial number of the genes that have their three parents [3(2 - F)], minus the average number of NIBD genes that reach their m representatives. The variable represented by this number was defined as Y m , and its average as E(Y m ), or that is, (NIBD) pt = 3(2-F) E(Y m ).
It was assumed that the parents of a TH are A 1 A 2, B 1 B 2 and C 1 C 2, and without loss of generality, this is represented as (A 1 A 2 x B 1 B 2) x C 1 C 2, with genotypic array [(AGE) CT ]:
Furthermore, their m representatives are the elements of a random sample taken with replacement of the population formed by its eight genotypes (Equation 1).
The possible results of the sampling with replacement of the offspring of a TH (Equation 1) include the extreme cases in which their m elements are the same genotype m times, and when the sample contains the eight genotypes of the progeny. For this latter case it is required that m≥8.
When m is large, there are a great number of possibilities of frequencies and orders of occurrence of the genotypes that integrate each sample, and in this case the number of different NIBD genes was determined (regardless of their frequency), and the number of forms (permutations) in which this number of genes may occur. When calculating the number of events that are equally possible and mutually exclusive that can be produced by the sampling (8m), calculations were made of E(Y m ) and the number of NIBD genes that are lost in the passing of the virtual population of a TH (genotypic array of Equation 1) to the sample that represents it.
Results and discussion
To derive a formula for E(Y m ), it was considered that the sample of m size with replacement extracts g genotypes of those indicated in Equation 1 (g=1, 2,..., 8) and was defined as:
1)
2)
Two quotients were constructed with both terms with which the following can be calculated:
1) The number of forms in which any g genotypes can occur in the sample with the k-th set of g frequencies of the type
The number of permutations to assign the g elements of the k-th set of frequencies to two separate genotypes of the sample
Whatever the form of association between frequencies and genotypes, the number of NIBD genes they supply is the same.
The product
If from the r-th group of
In a sample of m size the number of different genotypes (g) may be 1, 2, 3, ..., 8 (when ≥38). Furthermore, the number of sets of frequencies depends on g(k = 1, 2, 3, ..., Ug). With both considerations and by Equation 4, the expected number (average) of NIBD genes in the m representatives of a TH [E(Y m )] is:
As the number of NIBD genes that contain the genotypic arrangement of a TH is 3(2-F), the average of NIBD lost by each three-way hybrid [(NIBD)pt] was expressed as follows:
As an example, when m = 12 and g = 6, let’s say G 1, G 2, ..., G 6, there are 11 sets of possible frequencies in which the six genotypes may occur (k = 1, 2, ..., 11; Table 1). If k = 1(set of frequencies for any six genotypes in which each one of five of these occurs once and the sixth one occurs seven times), the frequencies can be associated to the six genotypes in six different forms [6!/(5! 1!) = 6]. Furthermore, the number of forms in which these six genotypes can occur with m = 12 is 12!/(1!1!1!1!1!7!) = 95,040 [Table 1].
Table 1 Three characteristics of the random sampling with replacement when m = 12 and g = 6 of the genotypic array produced by (A
1
A
2
x B
1
B
2
) x C
1
C
2
: 1) the 11 possible sets of genotypic frequencies (k), 2) the permutations for associating the frequencies of each set to the six genotypes
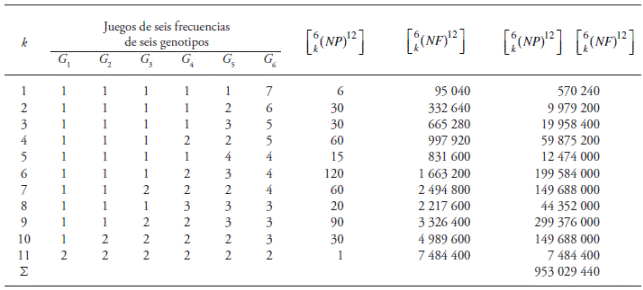
In this example, for each one of the 28 different sets of six genotypes the possible sets of frequencies are 11. Complementarily, the numbers of forms of assigning the frequencies of each set are shown
If the six genotypes that appear in the sample were A
1
C
1, A
1
C
2, A
2
C
1, A
2
C
2, B
1
C
1 and B
1
C
2 (Equation 1), they would supply 5-2F genes NIBD. Based on the above, the information in Table 1 and applying Equations 1 to 4, their contribution when
To determine the total contribution when m = 12 and g = 6, we should consider the contribution of the remaining 27 sets of six genotypes which may be produced by the sampling and the amount of NIBD genes that each one contains (Table 2), as well as all of the data that permit the determination of E(Y m ) for each one of the 11 values of m (Table 3).
Table 2 Examples of sets of g genotypes (g = 1, 2, 3, ..., 8) that contain ym genes not identical by descent and number of possible cases. The genotypes are obtained by random sampling of m size with replacement of the set of the eight genotypes produced by the cross (A1A 2 x B1B 2 ) x C1C 2 (Equation 1).
| g | Ejemplos | y m | Casos posibles | g | Ejemplos | y m | Casos posibles | |
| 1 | A 1 C 1 | 2 | 8 | 5 | A 1 C 1, A 1 C 2, A2C1, | |||
| A 2 C 2, B 1 C 1 | 5 - 2F | 24 | ||||||
| 2 | A 1 C 1, A 1 C 2 | 3 - F † | 8 | A 1 C 1, A 1 C 2, A 2 C 1, | ||||
| A 1 C 1, B 1 C 1 | 3 | 8 | B 1 C 1, B 2 C 1 | 6 - 3F | 32 | |||
| A 1 C 1, A 2 C 2 | 4 - 2F | 4 | ||||||
| A 1 C 1, B 1 C 2 | 4 - F | 8 | 6 | A 1 C 1, A 1 C 2, A 2 C 1, | ||||
| A 2 C 2, B 1 C 1, B 1 C 2 | 5 - 2F | 4 | ||||||
| 3 | A 1 C 1, A 1 C 2, A 2 C 1 | 4 - 2F | 8 | A 1 C 1, A 1 C 2, A 2 C 1, | ||||
| A 1 C 1, A 1 C 2, B 1 C 1 | 4 - F | 24 | A2C 2, B 1 C 1, B 2 C 1 | 6 - 3F | 24 | |||
| A 1 C 1, A 2 C 1, B 1 C 2 | 5 - 2F | 24 | ||||||
| 7 | A 1 C 1, A 1 C 2, A 2 C1, | |||||||
| 4 | A 1 C 1, A 1 C 2, A 2 C 2, B 1 C 1 | 5 - 2F | 50 | A 2 C 2, 1 | ||||
| A 1 C 1, A 1 C 2, B 1 C 1, B 1 C 2 | 4 - F | 4 | B 2 C 1 | 6 - 3F | 8 | |||
| A 1 C 1, A 2 C 1, B 1 C 1, B 2 C 2 | 6 - 3F | 14 | ||||||
| A 1 C 1, A 1 C 2, A 2 C 1, A 2 C 2 | 4 - 2F | 2 | 8 | A 1 C 1, A 1 C 2, A 2 C 1, | ||||
| A 2 C 2, B 1 C 1, B 1 C 2, | ||||||||
| B 2 C 1, B 2 C 2 | 6 - 3F | 1 |
Table 3 Number of forms of occurrence of g genotypes in random samples of m size taken with replacement of the eight genotypes produced by the three-way cross (A1A 2 x B1B 2 ) x C1C 2 . If m = g, in addition to the number of forms, between parenthesis is the sum of genes not identical by descent supplied by the 8!/[(8 - g)!g!] possible sets of g genotypes. The case m = 11 is not included.
| m | g | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 8 (2) | |||||||
| 2 | 8 | 2!(96-24F)† | ||||||
| 3 | 8 | 6 | 3!(248-88F) | |||||
| 4 | 8 | 14 | 36 | 4!(358-150F) | ||||
| 5 | 8 | 30 | 150 | 240 | 5!(312-144F) | |||
| 6 | 8 | 62 | 540 | 1560 | 1800 | 6!(164-80F) | ||
| 7 | 8 | 126 | 1800 | 8400 | 16 800 | 15 120 | 7!(48-24F) | |
| 8 | 8 | 254 | 5796 | 40 824 | 126 000 | 191 520 | 141 120 | 8!(6-3F) |
| 9 | 8 | 510 | 15 882 | 186 480 | 834 120 | 1 905 120 | 2 328 480 | 1 451 520 |
| 10 | 8 | 1022 | 55 980 | 818 520 | 5 103 000 | 16 435 440 | 20 635 200 | 30 240 000 |
| 12 | 8 | 4094 | 519 156 | 14 676 024 | 165 528 000 | 953 029 440 | 3 162 075 894 | 6 411 968 640 |
Of the 28 different sets of six genotypes, four contain 5 2F NIBD genes each, and each one of the 24 remaining sets supplies 6 - 3F (Table 2). With the contributions of the 11 sets of possible genotypic frequencies (k = 1, 2, 3, ..., 11; Table 1), the total contribution can be calculated when m = 12 and g = 6 to E(Y m ). That is (Tables 1 to 3):
The obtainment of this result involved the consideration already evidenced that the 28 combinations of six of the eight genotypes of the offspring of a TH (Equation 1) have the same probability of occurrence in the sample. Furthermore, with m≥8, the results with respect to genotypes obtained in the random sample with replacement are all of the possible combinations that can be formed with g of the eight genotypes for each one of the possible values of g (1, 2, 3, ..., 8).
The information of Tables 2 and 3 make it possible to calculate the numerator of the quotient that permits the calculation of the average of NIBD genes that reach the m representatives of the threeway cross. The denominator (8 m ) is the number of results equally possible and mutually exclusive that can be produced by the sample; to define the numerator, it is necessary to calculate the number of NIBD genes supplied by each one of the 8 m possible cases (with 8≤m). For example, according to the information of Table 3, for m = 12, which allows the obtainment of samples that may contain 1, 2, 3, 4, ..., 7 or 8 genotypes:
This result, E(Y 12) = 5.8728 - 2.8733F, is important for breeders and specialists in genetic resources and is an indicator that one is close to what should be expected when m is “big”: no NIBD gene must be lost; that is, their number in the sample should be 6-3 F. From Table 4, various relevant facts are revealed: for a fixed value of F when m increases, E(Y m ) increases, and more rapidly when F is smaller. Furthermore, with pure lines (F=1), a sample of 10 individuals of a three-way cross is enough to reach the equilibrium in three NIBD genes, and therefore, zero genes are lost. On the other hand, with F=0.5, this condition begins to be ostensible with m=12. It is also inferred that when F=0.75, starting from m=15 there is no loss of NIBD genes.
Table 4 Numbers of genes not identical by descent expected [(E(Y m )] and lost [(NIBD) pt ] in samples of m size with replacement taken from the genotypic array of a three-way cross made with non-related lines (Equation 1) for five inbreeding coefficients (F). The case m=11 is not included.
| m | F = 0.00 | F = 0.50 | F = 0.75 | F = 0.875 | F = 1.00 | ||||||
| E(Y m ) | (NIPD) pt | E(Y m ) | (NIPD) pt | E(Ym) | (NIPD) pt | E(Y m ) | (NIPD) pt | E(Y m ) | (NIPD) pt | ||
| 1 | 2.00 | 4.00 | 2.00 | 2.50 | 2.00 | 1.75 | 2.00 | 1.38 | 2.00 | 1.00 | |
| 2 | 3.25 | 2.75 | 2.88 | 2.38 | 2.69 | 1.06 | 2.59 | 0.78 | 2.50 | 0.50 | |
| 3 | 4.06 | 1.94 | 3.41 | 1.09 | 3.08 | 0.67 | 2.91 | 0.46 | 2.75 | 0.25 | |
| 4 | 4.61 | 1.39 | 3.74 | 0.76 | 3.31 | 0.44 | 3.09 | 0.28 | 2.88 | 0.13 | |
| 5 | 4.99 | 1.01 | 3.96 | 0.54 | 3.45 | 0.30 | 3.19 | 0.18 | 2.94 | 0.06 | |
| 6 | 5.26 | 0.74 | 4.11 | 0.39 | 3.54 | 0.21 | 3.25 | 0.12 | 2.97 | 0.03 | |
| 7 | 5.45 | 0.55 | 4.22 | 0.28 | 3.60 | 0.15 | 3.29 | 0.08 | 2.98 | 0.02 | |
| 8 | 5.59 | 0.41 | 4.29 | 0.21 | 3.64 | 0.11 | 3.32 | 0.06 | 2.99 | 0.01 | |
| 9 | 5.69 | 0.31 | 4.34 | 0.16 | 3.67 | 0.08 | 3.33 | 0.04 | 2.99 | 0.01 | |
| 10 | 5.77 | 0.23 | 4.39 | 0.11 | 3.69 | 0.06 | 3.34 | 0.03 | 3.00 | 0.00 | |
| 12 | 5.87 | 0.13 | 4.44 | 0.06 | 3.72 | 0.03 | 3.36 | 0.02 | 3.00 | 0.00 | |
With an increasingly larger sample its number of NIBD genes tends to increase because each additional individual included is a new opportunity for it to have a genotype that supplies genes that were not yet part of that sample. This can have repercussions on the inbreeding coefficient; Márquez-Sánchez (2010) found that an SV formed with t THs (Sin t ) constructed with pure non-related lines has an inbreeding coefficient (FSin t ) equal to (3m + 1)/ (8tm). According to this result m is related inversely to FSin t and the number of NIBD genes lost is reduced, which would predictable when FSin t is larger.
For Busbice (1970), the coefficient of endogamy of an SV is linearly and inversely related to its genotypic mean. In this context, the inbreeding coefficients of a synthetic variety formed with an even number of pure L lines (Sin L ) and another formed with L/2 simple crosses (Sin CS ) made with the same pure L lines are not dependent on m, are equal to 1/L, and the genotypic means of the two synthetic varieties should be equal. However, if L is an even number and multiple of three, the inbreeding coefficient of a Sin t made with L/3 three-way crosses would be greater than 1/L according to the result reported by Márquez Sánchez (2010). Furthermore, in consistence with the equality of its inbreeding coefficients, if F=1 the Sin CS and the Sin L never lose NIBD genes when the sample is formed from the m representatives of each one parent; also, the m representatives of each parent have the same genotype. On the other hand, the Sin t loses NIBD genes (Table 4). Sahagún-Castellanos and Villanueva-Verduzco (2012) report losses of NIBD genes in synthetics formed only with double or single crosses (F<1).
Conclusions
Starting at the formation of the m individuals of each one of the parent three-way crosses, loss of NIBD genes may occur; this is higher when m is smaller and its parent lines have a lower inbreeding coefficient (F). In contrast, if F=1 a sample size of eight (m=8) is enough for this loss to be reduced to zero. If F=0.5 and m=12, the expected number of NIBD genes lost is 0.06. In addition, the imbalance of the genetic frequencies of the parents of each three-way cross produces a higher inbreeding coefficient in the Sin t than in the Sin L , which has a negative effect on the genotypic mean of the former.
Literatura citada
Busbice, T. H. 1970. Predicting yields of synthetic varieties. Crop Science 10: 260-269. [ Links ]
Escalante-González, J. L., J. Sahagún-Castellanos, J. E. Rodríguez-Pérez, y A. Peña-Lomelí. 2013. Erosión genética en las cruzas simples progenitoras de una variedad sintética. Rev. Chapingo Serie Hort. 19: 151-161. [ Links ]
Espinosa, C. A., M. Sierra M., y N. Gómez M. 2002. Producción y tecnología de semillas mejoradas de maíz por el INIFAP en el escenario sin la PRONASE. Agron. Mesoam. 14: 117-121. [ Links ]
Luna, M., A. Hinojosa R., O. Ayala G., F. Castillo G., y F. J. Mejía C. 2012. Perspectivas de desarrollo de la industria semillera de maíz en México. Rev. Fitotec. Mex. 35: 1-7. [ Links ]
Márquez-Sánchez, F. 2010. Inbreeding coefficient and mean of maize synthetics of three-way lines hybrid. Maydica 55: 227-229. [ Links ]
Pérez-López, F. J., R. Lobato-Ortiz, J. de J. García-Zavala, J. D. Molina-Galán, J. de J. López-Reynoso, y T. Cervantes-Santana. 2014. Líneas homocigóticas de maíz de alto rendimiento como progenitores de híbridos de cruza simple. Agrociencia 48: 425-437. [ Links ]
Sahagún-Castellanos, J., y C. Villanueva-Verduzco. 2012. ¿Variedades sintéticas derivadas de cruzas simples o de cruzas dobles? Rev. Chapingo Serie Hort. 17(3):107-115. [ Links ]
Received: October 2015; Accepted: August 2016











 texto em
texto em 


