I. Introduction
To define and quantify the quality of open water bodies many researchers in the field of environmental monitoring have utilised a number of parameters. For such quantification of water quality, several satellite-derived parameters were considered (Menken and Brezonik 2006; Philipson et al. 2016; Mushtaq and Lala 2017; Masocha et al. 2017). Various water quality parameters were derived using an airborne hyperspectral spectrometer (Koponen et al. 2002; Mobley et al. 2005). The most frequent parameters used are: chlorophyll-a, total suspended particles and transparency (Doña et al. 2014; Harvey et al. 2015). The transparency is determined by the Secchi disk depth (Song et al. 2011) and the suspended particles comprehend dead, inert and degraded organic matter (Reza 2008; Kilham at al. 2012; Yang et al. 2017). The transparency is inversely proportional to turbidity, the latter of which is determined by the absorption and scattering of light within a water column (Aguilar-Maldonado et al. 2017). The chlorophyll-a concentration is directly related to phytoplankton biomass and is used as an indicator for eutrophication (Menken and Brezonik 2006).
The Organization for Economic Co-operation and Development (OECD) defines eutrophication as the water enrichment in nutritive substances that generally leads to changes such as the increase in algae production and other aquatic plants, and the deterioration of water quality and aquatic ecosystem (Doña et al. 2014). The states of eutrophication are: ultraoligotrophic, oligotrophic, mesotrophic, eutrophic and hypertrophic. The water quality is inversely proportional to the degree of eutrophication. Other water quality parameters, related to biochemical and thermodynamic processes in inland waters, were considered using vector regression and neural networks modelling with a limited sampling (Wang et al. 2011). The distribution of superficial temperature was also considered as an indicator of water quality (Korosov et al. 2007). For remote sensing studies of water quality using satellite images, only parameters with an optical response can be considered. A multivariate analysis of temperature, salinity and dissolved oxygen was performed using cluster analysis, principal component analysis and partial least square to assess the water quality of a coastal lagoon (Basatnia et al. 2018). The results indicated the critical need to monitor coastal water on a regular basis.
To retrieve water quality parameters from a multispectral satellite image, four different methods were applied (Campbell et al. 2011; Gholizadeh et al. 2016): (i) the look up table approach that compares the measured spectra response of optical water constituents with stored spectra; (ii) the neural network method that compares a large number of training data spectra to the measured spectra (Pozdnyakov et al. 2005a; El Din et al. 2017); (iii) the emPirical-regression that relates a linear combination of image bands with in-situ measurements (Bilge et al. 2003; Ficek et al. 2011; Lessels and Bishop 2013; Doña et al. 2014; Bonansea et al. 2015); (iv) the inversion/optimization method to simulate the spectra from a set of parameters that minimizes a cost function (Campbell et al. 2011). All four methods require a multispectral satellite image with adequate spatial and temporal resolution and in-situ measurements gathered close in time to the date of image acquisition.
A review article that accounts for space borne and airborne sensors used in the assessment of water quality was published in the scientific literature (Gholizadeh et al. 2016). The authors of the review included a comprehensive discussion of sensors and methods used in the evaluation of water quality parameters.
The research published accounts for the spatial and temporal variations of water quality parameters. However, a model that combines such parameters to produce a single output map dePicting varying levels of water quality is still required.
In this research a probabilistic model combining several water quality parameters is proposed. The water quality parameters considered are: Turbidity, Chlorophyll-a, Vegetation Index and Superficial Temperature. A model that considers such parameters and produces a single image dePicting the degree of water quality is required. The model reported in this research combines such parameters using a procedure, based on fuzzy logic, and derived from multivariate probabilistic logic (Nilsson, 1986; Adams, 1996; Zalta et al. 2019). Multivariate probabilistic logic has been used in the past to produce maps of primary productivity (Lira et al., 1992). An algorithm based on fuzzy logic was used to perform a multivariate fuzzy cluster analysis of open water bodies. Three clusters were obtained that represent three levels of water pollution (Wang and Wang 2009). These authors used hierarchical cluster analysis based on fuzzy cluster and multivariate statistical techniques. Such statistical techniques did not consider a multivariate probabilistic analysis. Rather, the authors employed sampling of water bodies to perform a classification of three levels of water pollution.
Details on the calculation of parameters are provided. A description of the basic principles of multivariate probabilistic logic and its application to model water quality are given. The area of study is the Centla Wetlands located in South East Mexico where numerous water bodies in varying degrees of eutrophication are observed (Guerra-Martinez and Ochoa-Gaona 2006). An example is provided and a discussion of results is included.
II Materials and Methods Materials
II.1 Materials
A wetland is a natural system defined as an extension of salt marshes, marshes, covered with water, regime natural or artificial, permanent or temporary, suspended or current, sweet or salty surfaces (Fondriest 2016). One important characteristic of the wetlands is that the substrate is periodically saturated or covered with water. Such saturation sustains the development of the ground and the communities of plants and animals that inhabit the wetlands.
The Centla Wetlands are located in the State of Tabasco to the South East of Mexico (Figure 1). The State of Tabasco is divided into five subregions: (1) Chontalpa, (2) Center, (3) Sierra, (4) Wetlands, (5) Rivers (Rodriguez 2002; Guerra-Martinez and Ochoa-Gaona 2006). The Centla Wetlands are included in the subregions (2) and (3) (Figure 1). The area covered by the satellite image is appreciated in Figure 1. Such image was overlaid over the subregions. Such overlay hinders the boundaries of the subregions. If such boundaries were shown in figure 1, the Centla water bodies would not be appreciated in its full extent.
A detailed description of the open water bodies that form the Centla Wetlands is included in the work by Rodriguez (2002). General morphologic and hydrologic conditions of the water bodies are included in such description. Table 1 provides basic geophysical details about the subregions. To develop the model proposed in this research, a Terra/Aster image was acquired (Table 2 and Figure 1).
Table 1 Geophysical details of the subregions of Tabasco (location of the Centla Wetlands).
| Subregion | Area (Ha) | Precipitation (mm) | A v er a ge height (masl) |
| Chontalpa | 746,289 | 1,225 | 13.8 |
| Centre | 259,380 | 1,882 | 7.7 |
| Sierra | 184,727 | 3,711 | 24.7 |
| Wetlands | 663,568 | 1,225 | 1.7 |
| Rivers | 603,408 | 2,343 | 17.0 |
II.2 Methods
II.2.1 Preprocessing of Terra/Aster Image
Bands 1 - 9 of the Terra/Aster image were resampled to a Pixel of 15 x 15 m2, and geocoded to a UTM projection using the ephemeredes of the Terra/Aster Satellite (Table 2). An atmospheric correction was carried out using the method of dark object subtraction (Chavez 1996). A subimage was extracted to cover the area of the Centla Wetlands. The water bodies were segmented using a previous developed method (Lira 2006). The block diagram of Figure2 dePicts the preprocessing of the image. The atmospheric correction was applied to the Visible and Near Infrared bands (VNIR) (bands 1-3) and Short Wave Infrared bands (SWIR) (bands 4-9) (Table 2). The kinetic band for the derivation of superficial temperature was acquired with atmospheric correction. The acquisition date of the Terra/Aster image is in line with field data reported by Rodriguez (2002).
II.2.2 Water Quality Parameters
The notion of water quality is used to describe the condition of a water body. This includes the chemical, physical and biological characteristics to quantify the degree to which water is useful with respect to its suitability for a particular purpose (Bartran and Ballance 1996). In this research the purpose is to determine the degree to which water is clean. Therefore, the parameters selected to quantify water quality of the water bodies in the study area are: Turbidity, Chlorophyll-a, Vegetation Index, and Temperature. These parameters were selected on the grounds of methods and results published in the scientific literature. The rational and calculation of these parameters is provided in the following sections.
Turbidity
The turbidity is used as a unit of measure to quantify the transmission of radiation through a column of water. Turbidity is defined as the degree of the haziness in water caused by suspended solids. The radiation is scattered and absorbed by the presence of suspended organic and inorganic particles in the water. The scattering of radiation increases as the density of suspended particles becomes higher (Roberts et al., 1995) (Figure 3). The emPirical algorithms are derived from transfer radiation models that consider the spectral characteristics of suspended particles in the water (Ritchie et al. 2003). The scattering and absorption of radiation by suspended particles is a function of the wavelength (Bukata et al., 1995) (Figure 4). The depth of penetration of radiation is a function of the wavelength (Bukata et al., 1995) (Figure 5). The water bodies of the Centla Wetlands belong to Case II of inland waters (Pozdnyakov et al. 2005b). For this case, the model selected is
The histogram of the image produced by equation (1) was elongated to a range of [0,255]. Figure 6 shows the Turbidity for the area of study.
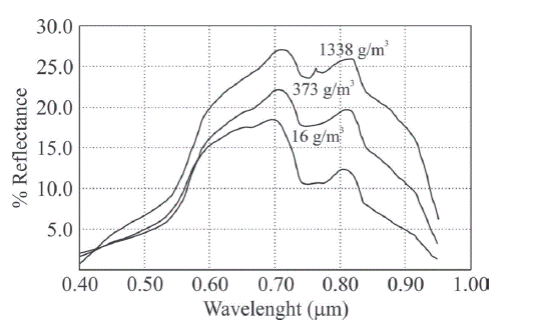
Figure 3 The reflectance of radiation as a function of the wavelength for several concentrations of suspended particles
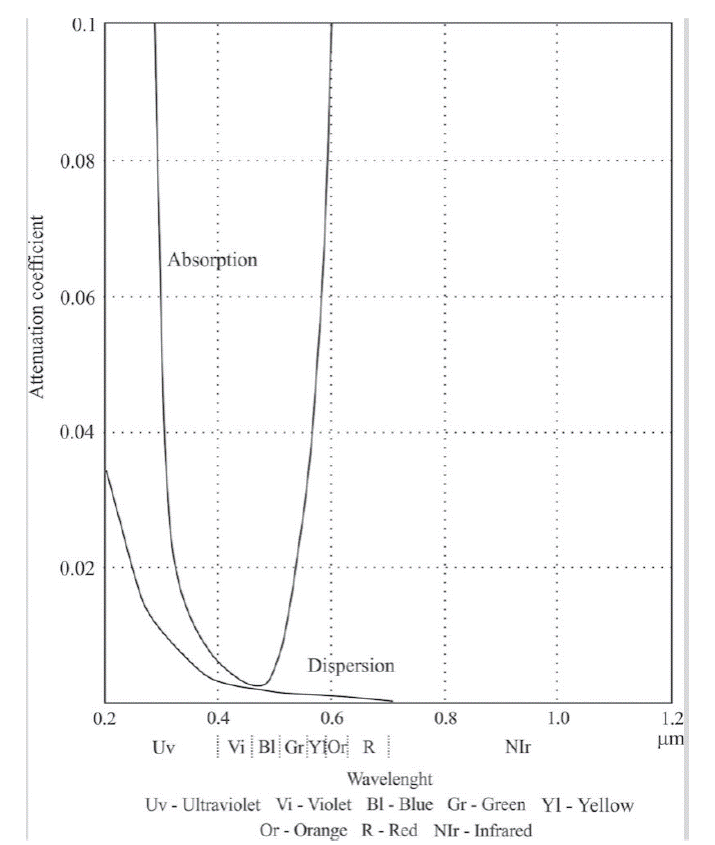
Figure 4 Attenuation of radiation as a result of scattering and absorption of radiation by suspended particles.
Chlorophyll-a
The Chlorophyll-a is a photosynthetic Pigment. The concentration of Chlorophyll-a provides an indication of the volume of aquatic plants present in a water column. This Pigment is present in all groups of algae in coastal water bodies. The spectra for several concentrations of Chlorophyll-a shows a low reflectance in the bands corresponding to blue and red (Menken et al., 2006) (Figure 7). Instead, in the bands of green and near infrared, a high reflectance is observed (Figure 7). On the grounds of the behaviour of such spectra (Doña et al., 2014; Bonansea et al., 2015), the model to calculate Chlorophyll-a is then
The histogram of the image produced by equation (2) was elongated to a range of [0,255]. Figure 8 shows the Chlorophyll-a for the area of study.
Vegetation Index
Algae are plants that may affect water quality adversely by lowering the dissolved oxygen in the water. Some species of macrophytes in wetland areas can be detected by remote sensing. Species such as hydrilla and salvinia can be found in the area of study. In particular, salvinia is a floating plant in warm water bodies. The raPid growth rate of such plants can lead to a decrease in oxygen concentrations. The NDVI is used to estimate the presence of floating vegetation in the water bodies. The NDVI is defined a
The histogram of the image produced by equation (3) was elongated to a range of [0,255]. Figure 9 shows the Vegetation Index for the area of study.
Superficial Temperature
Temperature may be defined as a measurement of the average thermal energy of a substance. The solubility of oxygen and other gases will decrease as temperature increases. Therefore, an increase in temperature brings a decrease in water quality. The image of kinetic temperature was acquired from LP DAAC (Land Processes Distributed Active Archive Center) of NASA (National Aeronautics and Space Administration). This temperature image was generated from the five thermal bands (TIR); its original dimensions were 700 x 830 Pixels with a Pixel of 90 x 90 m2. A reformat was applied to generate an image of the same size as the VNIR bands with a Pixel of 15 x 15 m2. On the grounds of Planck law, the temperature emissivity algorithm was applied to the TIR bands. Such bands were previously corrected by atmospheric effects. The histogram of the image produced by the emissivity algorithm was elongated to a range of [0,255]. Figure 10 shows the Superficial Temperature for the area of study.
II.2.3 Multivariate Probabilistic Model
Nilsson (1986) first used the term probabilistic logic, where the truth-values of sentences are probabilities. The proposed semantical generalization induces a probabilistic logical entailment or logical consequence. If the probabilities of the argument premises are known, then the probability of its conclusion may be derived (Adams 1996; Zalta et al. 2019). In this sense, the multivariate probabilistic model is based on the fact that probability functions can be assigned to logical sentences such as
These sentences read as follows: if indicator Pi exists, the natural process Q exists with a certain probability. Such probability is given by the density functions derived from indicator Pi. The implication Pi = = > Q, is a fuzzy set. If the value of the indicator Pi changes, the probability of the state of the natural process Q changes as well. In he multivariate probabilistic theory, the variables Pi are named indicators. In this research, the variables Pi are identified as the parameters described in Section II.2.2. The natural process Q is identified as the water quality. In the scientific literature, the physical quantities: Turbidity, Chlorophyll-a, NDVI and Superficial temperature are considered as parameters. The water quality is the variable that depends upon such parameters.
In an image, the value of indicator Pi, varies from one location to another, i.e., from Pixel to Pixel. A Pixel, defined as an elementary cell (k,l), implies that the logic sentence Pi ==> Q, is extended to every cell (k,l) where these are the coordinates of a Pixel in the image of a parameter.
Due to the fuzziness of the sentence Pi ==> Q, there is some degree of redundancy among indicators (Table 3). The correlation matrix (Table 3) indicates low correlation among the indicators. Therefore, the probability of the occurrence of Q should be evaluated when its corresponding indicators occur simultaneously. For such evaluation we consider the intersection of every set determined by various indicators as
The logical interpretation of this sentence is: if all indicators Pi occur simultaneously, the process Q can be calculated with some degree of probability.
Table 3 Matrix correlation among water quality indicators
| Chlorophyll-a | NDVI | Temperature | Turibidity | |
| Chlorophyll-a | 1.0000 | -0.13327 | -0.28643 | 0.74188 |
| NDVI | -0.13327 | 1.0000 | -0.28030 | -0.38962 |
| Temperature | -0.28643 | 0.28030 | 1.0000 | -0.30620 |
| Turbidity | 0.74189 | -0.38962 | -0.30620 | 1.0000 |
| Parameter Pi | Implication | Natural Processes Q |
| Chlorophyll-a | Increases | Water quality decreases |
| Vegetation index | Increases | Water quality decreases |
| Superficial temperature | Increases | Water quality decreases |
Equation (5) may be rewritten as
Expression (6) is written explicitly as (Adams 1996; Zalta et al. 2019; Doménech et al, 2017)
Since Pi = = > Q are sets, equation (7) is equivalent to
The right term of equation (7) is the probability P of the occurrence of the process Q.
Since expression (8) is valid for every cell (k,l), the result is a spatial distribution of P. The result of P is an image where the probability of occurrence of Q is dePicted. The model (Expression 8) is dependent on the probability functions associated to the logic sentence Pi = = > Q. These functions must be modelled analytically or as tables supported by geophysical and biochemical principles and field data (Lira et al. 1992). In this research the probability functions are chosen as the density function associated to the Pixel values of each indicator. The histogram of the image parameters is a good approximation of the density functions (Figure 11). Since the histograms of image parameters are in the range [0,255], equation (8) is written as
In brief: if Pi increases ==> Q decreases.
Equation (9) was applied to the parameters selected in this research and the results are shown in Figure 12. The result of equation (9) is a map dePicted as an image in figure 12. The digital values of such image were assigned colors using a linear function. The color scale at the bottom of figure 12 is the visual representation of the relation digital value o color.
III. Results and Discussion
The four parameters calculated in this research for the generation of a water quality thematic map are dePicted in: figure 6 - Turbidity, figure 8 - Chlorophyll-a, figure 9 - Vegetation index, figure 10 - Superficial temperature. The histograms of indicators are in figure 11. The thematic map is shown in figure 12 and the discussion is divided according to such parameters. On the grounds of the definition of water quality used in this research (Bartran and Ballance 1996; Fondriest 2016), a qualitative colour code was associated to the thematic map. Such colour code dePicts the degree of water quality in the area of study of this research.
Turbidity
The North-West corner of the turbidity image shows a portion of the Gulf of Mexico. Due to the high concentration of sediments in the near-shore of the ocean, the turbidity is high (Figure 6). The water bodies with a connection to the ocean show a high level of turbidity as well. The rivers and canals located to the West and East show a high turbidity. A group of water bodies located to the Centre-East of the image has a high turbidity, whereas the water bodies to the South and Southeast are dePicted with low turbidity.
Chlorophyll-a
The Chlorophyll-a is high in the water bodies located to the Centre-East and Centre-South of the image (Figure 8). A high value is also observed in the near-shore ocean. An elongated body connected to the ocean shows a gradient of values for the whole set of parameters. A body in the centre of the image shows a high level of Chlorophyll-a. Other bodies located to the South-West show high values as well.
Vegetation index
Small bodies in the Centre-North and South West are dePicted with high values of the vegetation index (Figure 9), while medium values are observed in the bodies to the South. The bodies connected to a river and to the ocean have a low value. Rivers and canals are observed with medium values. The near-shore ocean shows the lowest value.
Superficial temperature
The superficial temperature shows moderate values for medium size water bodies isolated from rivers or canals (Figure 10). The two large bodies located at the centre of the image appear as high temperature. A group of small bodies to the Centre-North have high temperature as well. The elongated body to the North, with connection to the ocean, appears with a gradient of temperature.
Thematic map
Figure 12 shows the thematic map derived from the model proposed in this research. A qualitative colour scale is included to indicate the levels of water quality. In general, isolated small water bodies have an appearance of high quality. The water bodies located to the South show medium and high quality, and the near-shore ocean and the water bodies connected to the sea appear with low water quality. Several bodies are dePicted with a gradient of water quality.
IV. Conclusions
Four parameters related to water quality published in the scientific literature, were calculated using a Terra/Aster image that includes the thermal band. The parameters were obtained on the grounds of well-known algorithms reported in several instances in the scientific literature. Such parameters were used in a multivariate probabilistic model to produce a thematic map of water quality for open water bodies. At present, water quality has been determined on the grounds of one parameter or several parameters but taken separately. The model suggested in this research, considers the joint use of the four most frequently reported parameters for water quality. A map is derived using equation (9). However, no quantitative scale yet has been defined. More work is required in this sense.
At present, no joint use of such parameters has been reported in the literature and no quantitative scale of water quality has been defined. The term water quality is usually employed with respect to its suitability for a particular purpose. In this research water quality is understood as the degree to which water is clean. A water is clean when it served the purpose of human consumption. Human consumption is understood in this work as water suitable for drinking ingestion and agricultural use. Thus, a high quality water body as derived in the present research may be considered as water adequate for human consumption. Therefore, a qualitative scale was associated to the colour-levels indicated in the water quality thematic map. Most of the water bodies show a gradient and a complex pattern of water quality. The water bodies to the South and Southeast exhibit a uniform degree of high water quality. All isolated water bodies appear with high values of water quality. The lowest quality observed was in the bodies that have some sort of connection to rivers and the ocean.
The map shown in figure 12 may be used to determine potential uses of the water for human consumption or agriculture. A good quality of the water is the most important asset to decision makers as discussed in the introduction. A possible area of application of the model developed in this research may be the complex of lagoons in the area of TamPico-Altamira. The water of such lagoons is employed for human consumption; a critical decision must be made in this regard.











 nueva página del texto (beta)
nueva página del texto (beta)












