PACS: 25.60.Pj; 21.60.Ev; 24.10.Eq.
1.Introduction
In the past few decades, the large number of theoretical and experimental efforts has been concentrated to investigate the role of the nuclear structure degrees of freedom of collision partners on fusion process. The fusion reactions, wherein the colliding nuclei leads to the formation of a compound nucleus either by overcoming or by quantum mechanical tunneling through the Coulomb barrier, have emerged as one of the most sensitive nuclear spectroscopic tool to examine the role of the nuclear structure of the participating nuclei as well as their nuclear interactions 1,2,3. Despite of the lots of investigations done so far, the dynamics of fusion reactions still shows unexpected facets and attracts researcher to explore many unexplored features. Many theoretical and experimental evidences showed that the sub-barrier fusion excitation function data of various fusing systems is dramatically enhanced over the predictions of the one-dimensional barrier penetration model. Such fusion enhancement at near and sub-barrier energies has an intimate link with the nuclear structure degrees of freedom such as permanent deformation (deformed nuclei), vibration of nuclear surface (spherical nuclei), rotations of nuclei during collision, neck formation and nucleon (multi-nucleon) transfer reactions 1,2,3,4. The coupling of such dominant intrinsic channels to the relative motion of the collision partners effectively reduces the interaction barrier between the colliding systems and consequently results in an anomalously large fusion excitation functions at below barrier energies. Within the coupled channel approach, the effect of inclusion of intrinsic channels associated with the colliding systems is to replace the nominal Coulomb barrier by a distribution of barriers of different height and weight. In barrier distribution, the presence fusion barriers whose heights are smaller than the Coulomb barrier allow the passage of flux from entrance channel to fusion channel and hence coupled channel calculations are capable of reproducing the observed fusion dynamics 5-6.
In theoretical description, the influences of the relevant intrinsic channels are incorporated through the nucleus-nucleus potential. In this respect, the choice of nuclear potential is very crucial in order to judge the success of the theoretical approach. In heavy ion fusion reactions, the optimum choice of the nucleus-nucleus potential, which consists of the Coulomb repulsive interaction, centrifugal term and short range attractive nuclear potential, strongly affects the magnitude of fusion excitation functions and hence an accurate knowledge with regard the nuclear potential greatly simplifies the problem of understanding of the basic mechanism involved in the nuclear reaction dynamics 7 ,8,9,10,11,12,13,14,15,16,17,18,19,20. The nuclear potential of the Woods-Saxon form, wherein the depth, range and diffuseness parameters are interrelated, is often used to preview the various features of the heavy ion collisions. For this potential, the different sets of potential parameters are associated with different nuclear interactions between the collision partners. In case of elastic scattering analysis, a diffuseness of a = 0.65 fm is the most suitable for good description of the data. In contrast to this, a much larger value of the diffuseness parameter ranging from a = 0.75 fm to a = 1.5 fm has been extracted from the systematics of the fusion reactions 21 ,22, 23. This diffuseness anomaly, which might preview the various static and dynamical physical effects, is one of the interesting and challenging issue of heavy ion collisions. For heavy ion reactions, the recent analysis16,24,25,26,27,28 suggested that the energy dependence in nucleus-nucleus potential is another essential feature of nuclear potential. Such energy dependence is also pointed out in double folding potential wherein it originates from the nucleon-nucleon interactions as well as the non-local quantum effects. The non-local quantum effects are directly linked with the exchange of nucleons between the colliding systems and consequently generate a velocity dependent nuclear potential16,24. The energy dependence of the local equivalent potential is related to the finite range of Pauli nonlocality which in turn manifests the exchange of nucleons during nuclear interactions 16,24. It is quite interesting to note that the energy dependence in nucleus-nucleus potential is also reflected from the microscopic time-dependent Hartree-Fock theory 25,26,27, 28 . In Ref. 25 to 26, it has been shown that in the domain of the Coulomb barrier, the nuclear potential becomes energy dependent and such energy dependence occurs due to coordinate-dependent mass and the involvement channel coupling effects associated with the collision partners. In this sense, the energy dependent nuclear potential may give better explanation of the many uncharted features of nuclear interactions. To include nuclear structure effects as well as the energy dependence in nucleus-nucleus potential, the earlier work undertook several efforts by introducing the energy dependence in the Woods-Saxon potential via its diffuseness parameter 29,30,31.
In this work, the fusion dynamics of
2.Theoretical Formalism
2.1. Single channel description
The total fusion cross-section within the framework of partial wave analysis is defined as
Hill and Wheeler proposed an expression for tunneling probability (
This parabolic approximation was further simplified by Wong using the following assumptions for barrier position, barrier curvature and barrier height 43.
with, VB is the Coulomb barrier which corresponds to ℓ = 0.
Using Eq. (2) to Eq. (5) into Eq. (1), the fusion cross-section can be written as
By incorporating the contributions from the infinite number of partial waves to fusion process, one can change the summation over ℓ into integral with respect to ℓ in Eq. (6). By solving the integral one obtains the following expression of the one dimensional Wong formula 43 .
In earlier work, the EDWSP model
4,
8-
9,
13,17-18,29,30,
31 successfully explores the fusion dynamics of various
heavy ion fusion reactions wherein the inelastic surface excitations and nucleon
(multi-nucleon) transfer channels are the most relevant intrinsic channels. This
work examines the fusion mechanism of different projectiles (
with
where
and
are the isospin asymmetry of fusing pairs.
In collision dynamics, the large number of static and dynamical physical effects occurs in the surface region of nuclear potential or tail region of the Coulomb barrier and consequently changes the parameters of nuclear potential. For instance, the variation of N/Z ratio of the colliding pairs, variation of surface energy and nucleon densities during nuclear interactions, the channel coupling effects like permanent deformation and low lying inelastic surface excitations of the colliding systems, nucleon (multi-nucleon) transfer channels, neck formation, dissipation of kinetic energy of the relative motion of the collision partners to their internal structure degrees or other static and dynamical physical effects generally occur in the tail region of the Coulomb barrier. These physical effects induce modifications in the values of the potential parameters and henceforth, results in the requirement of the different set of potential parameters for the different type of the nuclear interactions. In fusion dynamics, the diffuseness parameter of the static Woods-Saxon potential strongly alters the energy dependence of low energy fusion cross-section at near and below barrier energies and there is large number of experimental evidences wherein an abnormally large value of the diffuseness parameter is needed to explore the sub-barrier fusion data. The recently observed steep fall of fusion excitation function data at deep sub-barrier energy region in many medium mass nuclei, which is termed as fusion hindrance, can only be explained if one uses an abnormally large diffuseness parameter 2- 3. In addition, the nuclear structure effects present in surface region produce fluctuation in the strength of nuclear potential and this kind of fluctuation of nuclear strength is associated with the variation of the diffuseness parameter. It is worth noting here that the different channel coupling effects and non-local quantum effects which originate from the underlying nucleon-nucleon interactions induce the energy dependence in nucleus-nucleus potential. Therefore, to include all the above mentioned physical effects, the energy dependence in the Woods-Saxon potential was introduced via its diffuseness parameter. The energy dependent diffuseness parameter is defined as
The range parameter (r0) is an adjustable parameter and its value
is optimized in order to vary the diffuseness parameter required to address the
observed fusion dynamics of fusing system under consideration. In addition, the
value of the range parameter (r0) strongly depends
on the nuclear struc- ture of the participating nuclei and the type of dominance
of nuclear structure degrees of freedom and hence the different set values of
the range parameter (r0) are required to explain the
fusion dynamics of the different fusing systems. The potential parameters
(r0, a and
V0) of the EDWSP model are interrelated and the
change in one parameter automatically brings the corresponding adjustment in the
values of other parameters. In the present model, the value of
V0 depends on the surface energy and isospin
term of the interacting nuclei and the other two parameters
(r0 and a) are linked through
the Eq. (10). Therefore, the
values of the diffuseness parameter is directly related with the range parameter
(r0) which in turn geometrically defines the
radii of the fusing systems (
2.2Coupled channel description
The coupled channel method that provides an adequate description of the fusion dynamics of various heavy on fusion reactions at near and sub-barrier energies is the most fundamental approach. In this method, the influences of intrinsic channels associated with the fusing systems are properly incorporated 44,46,47,48. In coupled channel approach, the following set of the coupled channel equation is solved numerically.
where,
where, PJ (E) is the total
transmission coefficient corresponding to the angular momentum
J. The rotational coupling with a pure rotor and
vibrational coupling in the harmonic limit are considered in the coupled channel
approach. The rotational (
Where, RT is defined as
and
respectively. The Coulomb coupling matrix elements are computed by the linear coupling approximation and are defined as
and
for the rotational and vibrational couplings respectively.
3.Results and Discussion
The present paper systematically analyzed the fusion dynamics of various heavy ion fusion reactions within the context of the static Woods-Saxon potential and energy dependent Woods-Saxon potential model along with Wong’s approximation. The influences of nuclear structure degrees of freedom of the fusing pairs are investigated using the coupled channel calculations. In this work, the fusing systems are selected in such a way that the different projectiles: doubly magic (
Table I The deformation parameter (βλ) and the energy (Eλ) of the quadrupole and octupole vibrational states of fusing nuclei.
Table II The values of VB0, RB and ћω used in the EDWSP model calculations for various heavy ion fusion reactions.
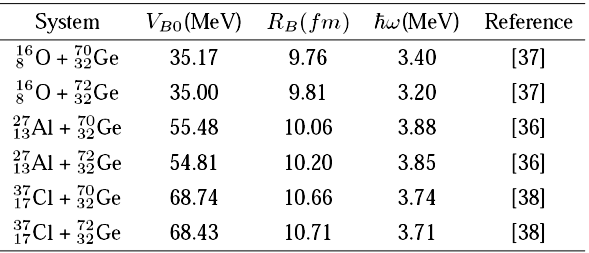
Table III Range, depth and diffuseness of the Woods-Saxon potential used in the EDWSP model calculations for various heavy ion fusion reactions 4,8-9,13,17-18,29,30,31.

The details of the coupled channel calculations for the fusion dynamics of
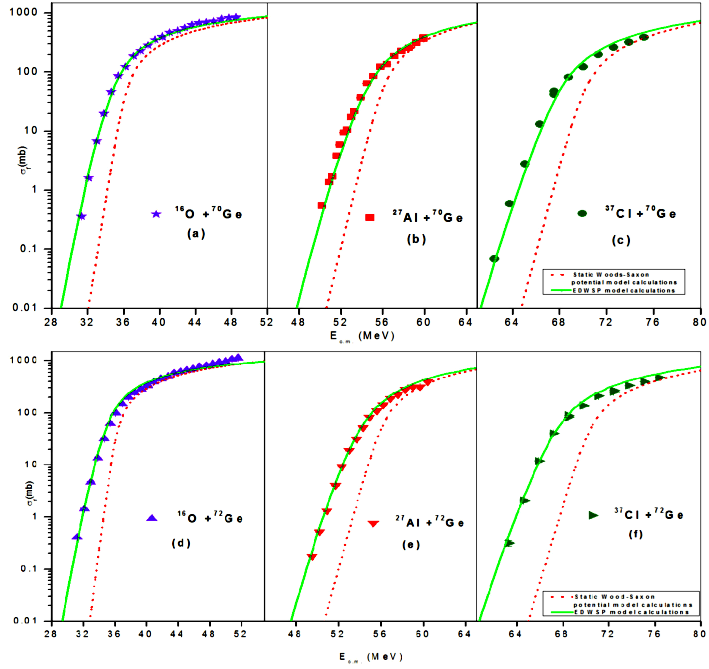
Figure 1 The fusion excitation functions of
The energy dependence in the Woods-Saxon potential modifies the barrier characteristics of the
interaction barrier between the colliding systems which in turn results in a
spectrum of the variable fusion barriers as shown in Fig. 2. The spectrum of the energy dependent fusion barrier is shown for
the
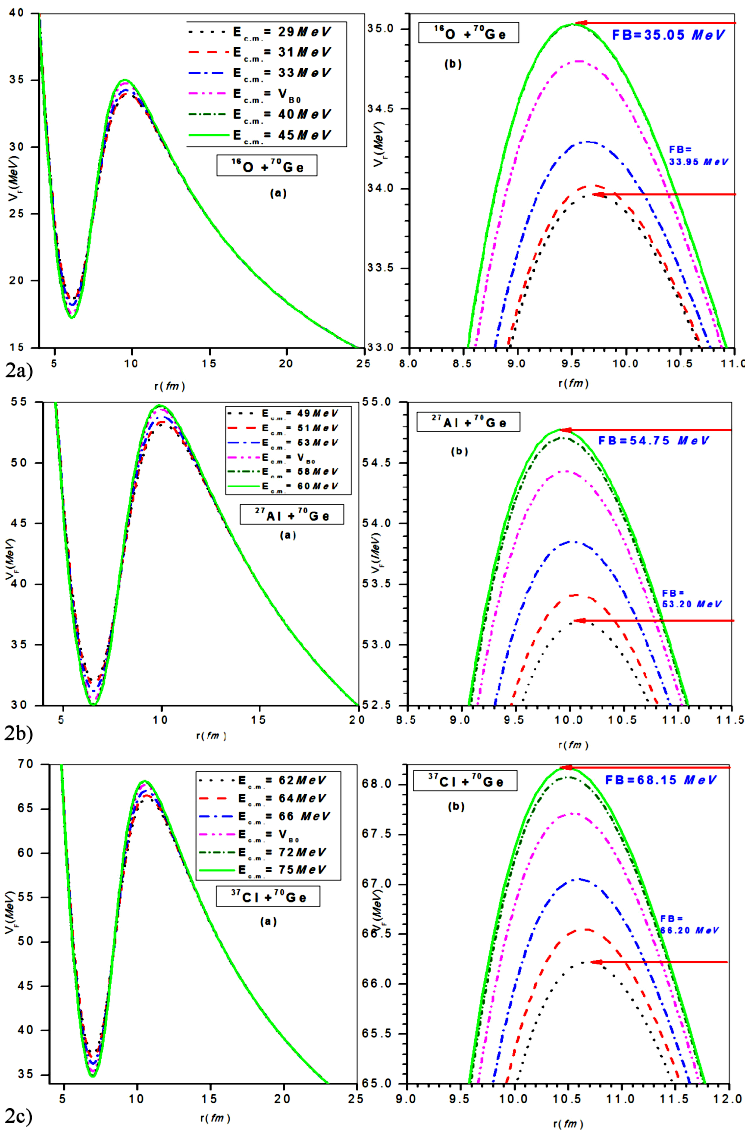
Figure 2 The fusion barrier (FB) for the
At above barrier energies, the fusion cross-sections are less sensitive towards nuclear structure as well as the channel coupling effects and consequently saturate at above barrier energies. This physical effect is properly modeled in the present approach wherein the magnitude of the diffuseness parameter gets saturated to its lowest value (a = 0.85 fm) at above barrier energies. At well above the barrier, the highest fusion barrier for the
Morton et al. 50 suggested
the weak influence of the collective vibrations of the
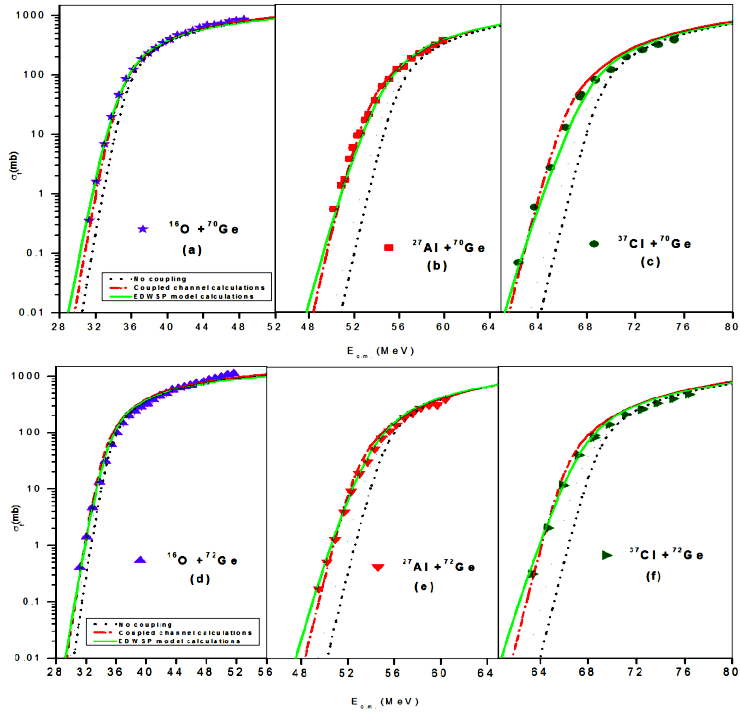
Figure 3 The fusion excitation functions of
The theoretical results of the fusion dynamics of
In Fig. 4, a comparison of the fusion excitation function
data of
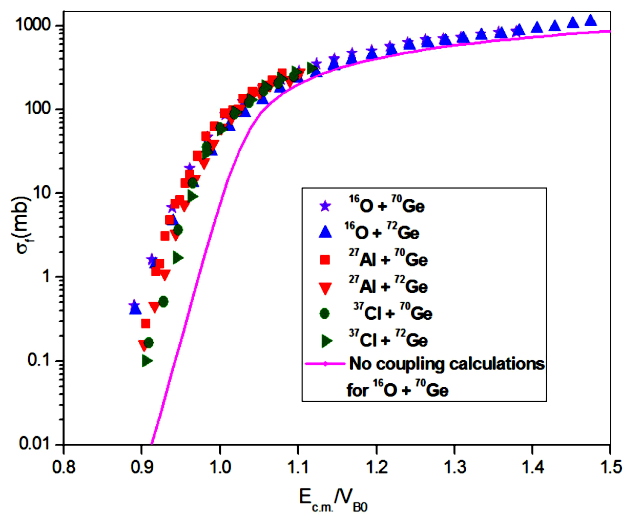
Figure 4 The fusion excitation functions data of
The different kinds of channel coupling effects display their signature on the fusion
excitation functions at sub-barrier energies while such physical effects have
negligible influence on the above barrier fusion data. Therefore, the one
dimensional barrier penetration model should provide a good description of the
fusion data at above barrier energies. In this sense, a comparison of above barrier
fusion data and the predictions of the present model for the fusion of
4. Conclusions
The present work analyzed the role of collective excitations of the fusing systems on the fusion mechanism of











 nueva página del texto (beta)
nueva página del texto (beta)



