1. Introduction

Several X-ray diffraction measurements of textured polycrystal pole figures have shown that density maxima of second order reflections are almost systematically larger than those of first order reflections of the same sample plane. For example, the pole density maximum of vacuum annealed silver with a conventional recrystallization texture (dominant component [110] ⟨011⟩) is 6.1 for pole figure 111, and 9.2 for pole figure 222, both measured with Kα Mo radiation. Alternatively, a similar sample, annealed in oxygen atmosphere, shows maxima of 11.9 and 14.6 for pole figures 111 and 222 respectively, when measured with Kα Cu radiation. It is expected that pole figures have to be identical for different reflection orders because they are produced by the same crystallographic planes. Consequently, measurements as those above described have motivated the assumption that diffraction from polycrystals is affected by the extinction phenomenon. This is clearly relevant for single crystals where first order reflections are affected more strongly than second order reflections. However in the case of polycrystals, if secondary extinction is noticeable, it has to be one of the main causes on the above mentioned pole density differences. This has led us to investigate systematically on the differences of pole figures^1,2,3 However, determination of pole figures requires several steps of calculations, namely: background subtraction, defocusing correction and normalization, and as result, error propagation could have different effects on both first order and second order reflections, since they exhibit strong intensity differences. Additionally normalization needs all measured intensity values. This includes zones with poor statistics as pole figure edges, and this could have a large influence in biasing pole density maxima.

A method has been devised here to verify if secondary extinction is present in textured polycrystals, by a detailed consideration of intensities of multiple scattering in a more direct way. This is justified to avoid large error propagation from lengthy calculations and normalization. As it is well known, secondary extinction in mosaic crystals is observed in rocking curves measurements, where the Ewald sphere presents essentially only one possible reflection, and the possibility of a second reflection only in a direction very close to the primary beam. In such a case, secondary extinction results as an absorption term of the form gPQ where g is inversely proportional to the width Δ of the crystallite orientation distribution, P depends on polarization, and Q is the integrated reflection per unit volume ⁴. This absorption term is comparable to the true absorption coefficient μ, for characteristic Δ values of mosaic crystals, i.e. minutes or seconds of arch. In principle the extinction absorption term can be negligible for misorientation widths found in polycrystals even with a sharp texture. Nevertheless, the Ewald sphere becomes a set of concentric shells in polycrystals, and many other possible secondary reflections take place, contributing to the intensity loss as registered by the detector, i.e. to secondary extinction. Also, in textured polycrystals a rocking curve is not a sharp peak, but a “mountain” composed by several local texture components. It is therefore unsuitable for extinction determination. Instead a detector scan is appropriate. It should also be mentioned that the irradiated volume remains constant in a detector scan, as well as in pole figure measurements by the Schulz reflection method. This volume depends only on the beam cross section and μ.

In the following, the integrated intensity of secondary D-S rings of a textured sample is evaluated, and compared for first and second order diffraction conditions of a general plane (hkl) after normalization by corresponding two theta scans of powder samples. Such rings arise from the diffracted beam, of two theta scans of eflections H = (hkl) and 2H = (2h, 2k, 2l). Differences from these reflections would indicate the extent secondary extinction affects pole figure determination.

2. Theoretical procedure

Let a two theta X-ray diffraction scan be measured in a sample in the form of a conventional plate, oriented at the angles (χ, φ) as for the measurement of a pole figure point for a reflection H = (hkl), χ is the tilting angle and φ is the angle of rotation around the sample normal. Let this point be the maximum pole density of the pole figure, although it can be any other point of the pole figure, as long as sufficient intensity is obtained. Let the detector be in a position to receive the diffracted beam on the equatorial plane with wave vector k and θ the Bragg angle of reflection H, as shown in Fig. 1. Let also ω be an angle characterizing the points of any secondary D-S-ring, in the interval from 0 to 2π.

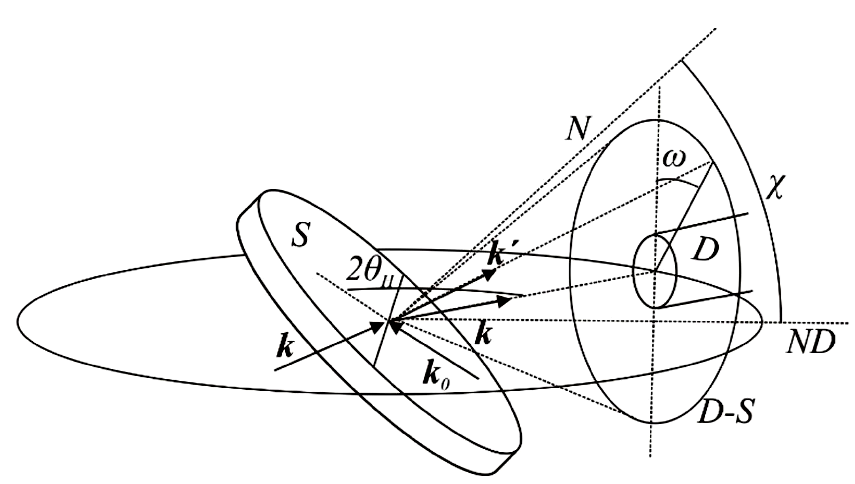
Figure 1 Measurement layout: S is the sample, k₀ and k are the incident beam and the diffracted beam wave vectors respectively, k0 is the wave vector of the twice diffracted beam. D-S is one of the set of secondary D -S rings produced by planes H´ and k now as the incident wave vector, ND is the conventional normal direction of the sample, N is the normal to the sample, which coincides with ND at the starting of a pole figure measurement, D is the detector. 2θ_H is the angle between k₀ and k, x is the tilting angle, and ω is an angle characterizing any point on the secondary D-S rings. 

The intensity of reflection H, denoted here as I_H (χ, φ), is not uniform along the D - S_H ring due to texture, and therefore not given by the well known expression for the intensity of powder. It must be modified by a factor η_H (χ, φ) which is the ratio of the diffracting crystallites volume V_H (χ, φ) of the sample, to the diffracting crystallites volume of powder. η_H (χ, φ) is therefore the pole density appearing in pole figures. V_H (χ, φ) is the volume of the crystallites diffracting in the direction of the detector, i.e. in a small segment of the D - S_H ring, proportional to the height of the detector slit. Since the aim of this investigation is a comparison of two orders of reflections from the same planes, only relative intensities are necessary, and so, we can write I_H (χ, φ) simply as

where IHP is the relative integrated intensity of the powder per unit arch length for the same reflection H, and d_H (χ) the defocusing factor, which for a fixed Bragg angle depends only on χ. IHP can be expressed as (See for example Eq. (4-21) of⁵):

with F_H the structure factor, p_H the multiplicity factor and e-2MH the temperature factor, for reflection H. Particularly, the absorption coefficient is considered constant, and therefore not included. This does not mean that absorption is considered negligible. Also, since intensity is measured as counts per second, no angular velocity of the detector is needed.

The intensity of the D-S ring of any of the secondary reflections H' of the textured sample is also non uniform due to texture, i.e. it depends on ω; the primary beam intensity is given by (1), and for the new incident wave vector the sample orientation (χ, φ) changes to some other orientation (χ', φ'). Furthermore, χ' and φ' become functions of ω. As result for any of the secondary diffraction events, a similar equation as (1) can be used, replacing η_H (χ, φ) by a function ρH'H(ω) . For any differential segment at the angle ω of the D-S ring of radius 1, the diffracted intensity is

This ring is not measured by the detector, and consequently there is no need to include defocusing.

The integrated intensity of the secondary D-S ring, J_H', is then

where VH'H is the total volume of crystallites diffracting on the H' secondary D-S ring, relative to powder, when the incident beam comes from reflection H.

It should be noticed that in (3) and (4), the incident beam for the second diffraction process is taken as the diffracted beam from the first diffraction process. Therefore this has to be taken only as an approximation, since the diffracted beam from the first process is not homogeneous.

The integrated intensity of all secondary D-S rings is then

And the intensity passing through the receiving slit and registered by the detector is

where

Multiple scattering is also produced in powders. In this case ρH'H(ω)=1, VH'H=2π and the corresponding ΔqH for powder is

the corresponding intensity arriving at the detector is

The normalized integrated intensity giving the pole density at point (χ', φ') of the pole figure is from (6) and (9)

And the corresponding normalized integrated intensity for the second order reflection 2H is

Comparison of these two expressions leads to the following: Any difference between ΔqH and Δq2H can only come through the coefficients VH'H and VH'2H, i.e. the total volume of the diffracting crystallites on every H' D-S ring. Actually, a difference in these quantities can be expected. The wave vector k generating the D-S rings for the first order diffraction, has a different direction as the one generating the D-S rings for the second order diffraction. However, in ΔqH, as well as in Δq2H, these volumes appear in a sum weighted by the power of the possible reflections. This should soften their individual differences, unless texture is very sharp and, consisting of a single dominant component. In this case the reciprocal space will be similar to the one of a mosaic crystal, and the theory of Zachariasen ⁴ becomes applicable. Nevertheless, since the crystallite misorientation breath is of the order of a degree, even for a very sharp texture, the absorption term due to secondary extinction is negligible. On the other hand, diffracted beam intensities are at least two orders of magnitude lower than the incident beam, and the second terms of Eqs. (7) and (8) should be negligible. This is certainly the case of (8) for a powder; however, every diffracting situation involves a large numbers of crystallite orientations in Eulerian space, defining a curve. If some of these curves cross zones of high pole density in the crystallite orientation distribution function (CODF) of a strongly textured sample, the second term of (7) could become significant. In the case of a powder, no volume differences are present because of the random orientation of the crystallites, and thus Δq2HP=ΔqHP, and to a good approximation

3. Secondary extinction correction

To obtain a viable secondary extinction correction method is beyond the scope of this work, although J_D-S in principle can fulfill this task if the quantities VH'H for possible reflections are calculated. However, this implies the knowledge of the density ρH'H(ω), which can only be obtained if the CODF is known, as it has been done in ³ for the case of neutron diffraction. The CODF used there was obtained by the conventional method of three pole figures as an approximation.

4. Discussion and conclusions

Equation (6) states that the integrated intensity of D-S rings is actually affected by secondary extinction. Additionally, Eq. (10) indicates that secondary extinction affects reflections of different order of a given set of planes approximately in the same proportion. If the present result can be experimentally verified, the implication is that observed systematic differences in the maxima of pole figures of reflections of different order, are to be attributed to error propagation. This can clearly affect both pole figures in different ways. Another likely possibility can be a heterogeneous texture, since first and second order reflections have small differences in penetration depth. If contrary to (10), i_H and i_2H show the same relation to each other as in pole figures at the maxima, this would suggest that primary extinction is present in those cases.

Two theta X-ray diffraction scans of rolled and annealed samples of cubic symmetry materials, whose textures are well known and consist of few dominant texture components, could be done to verify this theory.