1. Introducction

Thin folded matter configurations are present in nature. Some natural physical systems have a minimal state energy incrumpled configuration. Proteins are an example, and their properties have been studied ^1-3. Other systems like polymerized membranes ^4-7, graphene nanosheets ^8-13 and crumpled paper balls ^{14,15,17,19-27} have been well studied and they are reported in literature. Authors of ^{17,18,21,23-27} had made remarkable findings working with thin folded matter, particularly randomly crumpled paper. A complete study of mechanical and dynamical properties of crumpled paper balls and many different measurements of fractals quantities has been reported in ²⁶. In this sense the experimental and theoretical studies in crumpling phenomena is nowadays a very fertile area in science. Analytical relationships and numerical scaling exponents (fractal dimensionalities) have been stablished in relation to the morphological transformation of a flat sheet into a crumpled ball, and intensive studies over the recent decades had been made, fractal dimensionalities as chemical, random walk, shortest path, spectral, and others can be easily found ^{14,15,17,20-27}. As a practical model, paper crumpled by hand offers an attractive way to explore the nature of complexity, and also represents a good option to emulate some natural systems to extrapolate and correlate their properties. In the present work we will focus principally in just one fractal dimension of this set of universality class scaling exponents, this is the shortest path fractal dimension defined by the scaling relation ^26,28,29 (the present case: crumpled elastoplastic paper balls)

where l _min represents the chemical distance or shortest path and l _e the Pythagorean or Euclidean distance. The shortest path l _min is clearly defined between two vertices randomly chosen on the crumpling network. Initially this quantity was studied extensively by authors of ^18,28 for percolation cluster in 2D and 3D and re-write for the case of crumpling phenomena ^25,26. Authors of ²⁶ working with digitized images of stamped crumpling networks of paper balls got experimentally the d min value, finding that over 500 realizations dmin(2)=1.15±0.06 and dmin(3)=1.53±0.16 for the crumpling network in the flat and crumpled configurations respectively. In that sense this tedious but simple experiment looks for determining the shortest path fractal dimension between pairs of points randomly assigned on the surface of the cuasi-sphere paper balls correlating distances for the flat and crumpled configurations.

2. Experimental details and results

We started the experiment crushing by hand square sheets of copy paper type into quasi-spherical balls of diameter R, original sheet sizes edges were L = 12, 15, 22 y 30 cm. After we have turned a flat sheet into a ball we randomly assigned a collection of points on its surface and then a complete strain relaxation was permitted during 9 to10 days ^21,23. To identify each randomly assigned point, a color code was needed. 30 balls of each size were measured. In the crumpled state, a digital Vernier caliper was used to get the Euclidean distances, and in flat state measurements were made using the ruler tool of Foxit Reader free software ³⁰ after digitalizing the corresponding images of each different size sheet. The original form, crumpled and flat states of paper sheets, are shown in Fig. 1. Measuring the minimum distance between two points located in the same face of a sheet was an easy work, but in order to get measurements of distances of a pair of points in opposite sides of the flat sheet we devised the topological transformation presented in Fig. 2. For this case four distances data were obtained, the smallest one was chosen.

Figure 1 Copy paper type employed in the experiment. (a) Relaxed strain crumpled configuration and (b) Digitized sheet after being unfolded and flattened. The black corners were a guide to de eye. 

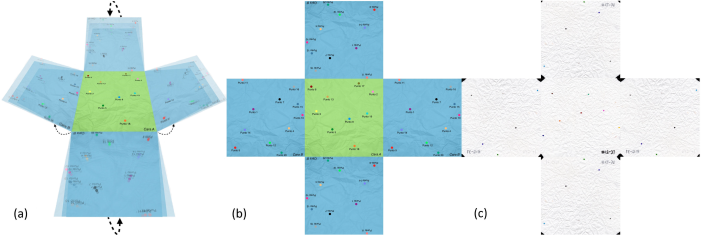
Figure 2 (a) and (b) images correspond to the topological transformation made on a virtual sheet just to show the process we followed, color points schematize the randomly assigned points on the surface of the crumpled ball, (c) image show a real one transformed digitized flatted sheet. 

Once final data were collected a statistic analysis procedure was started for each of the four sizes, we first began realizing a probability distributions tests in order to choose those ones that best fit to our length data ^{17,20,21,23,26,29}. We found that Gamma and Log-Normal distributions fitted very well in analogy with results of the study of length of crumpled creases reported in ^20,21,29. Figure 3 is an example of the procedure we followed. Here, we show this test data for the Euclidean distances, the cases of 12 cm size sheet and all sizes together are presented.

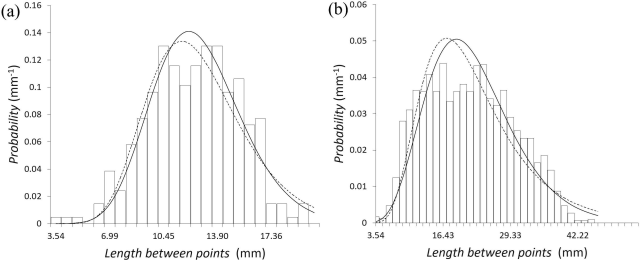
Figure 3 Statistical distributions of lengths between points randomly assignment on the surface of the hand crushed paper are shown. Curves: (a) 12 cm size paper; solid curve correspond to gamma distribution with α = 19:326 and ß = 0:6581, dashed curve corresponds to Log-Normal distribution with μ = 2:5143 and σ = 0:24918, (b) all the sizes of paper balls used in this work; solid curve correspond to gamma distribution with α = 6:9167 and ß = 3:2021, dashed curve corresponds to Log-Normal distribution with μ = 3:0165 and σ = 0:4202. 

For this work we took the Gamma probability distribution of this X ² tests for goodness of fit (following authors of [29]) to get the same-probability intervals to build graphs shown in Fig. 4 ^{17,20,21,23,26,29}.

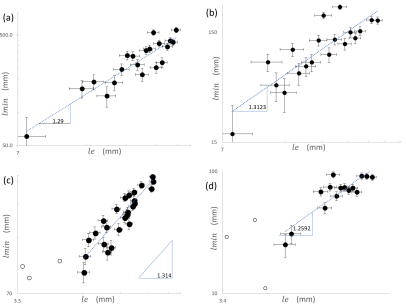
Figure 4 Log-log plots of chemical distances versus Euclidean distances between two any points are shown, data came from the randomly set of points on the cuasi-spheres surfaces averaged over 30 balls each. Fitting curves are l_min = 4:8091l¹ _e:²⁹⁶ ; R² = 0:8342, l_min = 1:9342 ^l _e ^1:3123 ; R² = 0:7302, l_min = 8:2132 ^l _e ^1:314 ; R² = 0:8114 and l_min = 1:2592 ^l _e ^1:2592 ; R² = 0:7636; for (a) 30 cm, (b) 22 cm, (c) 15 cm and (d) 10 cm respectively. Uniquely solid circles are considered, empty circles are excluded from fitting in all cases. 

A resume of the referred quantities is shown in Table I.

Global mean value can be written as

It is interesting to point out that, by definition, the chemical fractals dimensions in flat an crumpled configurations are both equal (dlball=2); Even more, these quantities with mass fractal dimension ^23,26 Dl (≈(8/3)) where dminball represents the shortest path fractal dimension in a folded ball of thin sheet.

Is important to note that (3) is just valid for elastoplastic sheets, and correspond to a fractal property of crumpling network in the folded configuration. In that sense we postulate that (2) could also be universal, because for elastoplastic paper sheets it has been shown ^21,23 that D _l is universal only after a complete relaxation of the elastic tensions due to self-avoiding interactions.

In Fig. 4 we can see the log-log plot made for each size sheet, in total more than 5500 measurements were realized and graphs exhibit that dmin for this experiment is independent of the sheet size L.

3. Discussion

Notwithstanding we did not smooth or neglect points except empty circles in last two cases (we are presenting the original set of resulting points), percentage error between expressions (2) and (3) is almost 3 percent. We believe that numerical result described by (2) for the shortest path fractal dimension may have a different meaning than just a coincidental value when compared with (3). But more interesting is the fact that (2) is also closely near up to one decimal to results of Monte Carlo simulations, reported by Zongzheng et al. in ¹⁸ as dmin=1.3756 and older simulation made by Hans and Eugene ²⁸ as dmin=1.34±0.01, both cases for three-dimensional percolation clusters. Despite the technical limitations and the errors induced during the measurement process, the resemblance of value (2) with shortest path fractal dimension for 3D percolation system also could be not a coincidence. In this sense, we suggest that a paper ball system under certain conditions can be viewed as an incrustation in a three-dimensional percolation cluster, in that way any random pair of superficial points are contained inside the cluster, set of points randomly assigned on the ball plays the role of randomly points arbitrarily chosen inside of the percolation system. from a statitical point of view, individual results do not give much information. But when he results from differente sizes of sheets became similar, it tells us that we can be dealing with the same kind of universality among other fractals dimensionalities, as suggested in ²⁶. We want to emphasize that results presented here were obtained for copy paper type sheets. However, it has been shown in experiments with different kind of elastoplastic thin sheets folded by hand, that the internal structure of the balls after a complete strain relaxation, obeys not only scale invariance but D _l is not material dependent ²³. On the other hand, authors of ³¹ had made a study of the lateral deformations for axial a radial confinement in plastic and elastoplastic thin sheets finding that just elastoplastic sheets obey a power law behavior, showing this that plastic thin sheets belong to a different universality class. In that sense, we expect that our results are generally valid for thin self-avoiding elastoplastic matter after the corresponding strain relaxation.

4. Conclusions

In conclusion, we determined the shortest path fractal dimension dmin for a crumpled elastoplastic paper ball relating measurements of length in crumpled and flat configurations to be 1.2953±0.02. That result is independent of the sheet size L. We think that numerical resemblance with percolation system is not just a numerical coincidence, even more, we postulate that a paper ball system can emulate in some manner a subsystem of type like the three-dimensional percolation one.