1. Introduction
Stimulated Raman adiabatic passage (STIRAP) [2-9] is a beautifully developed and robust technique that allows the precise control of population transfer from one quantum state to another in three-level quantum systems. In this technique the Stokes pulse, linking the initially unpopulated ground state to the exited state, arrives before the pump pulse, linking the initially populated ground state to the exited state. Fractional stimulated Raman adiabatic passage (F-STIRAP) [10, 11] is a change of STIRAP, which allows the creation of any preselected coherent superposition of the two ground states in a three-level Λ system. In F-STIRAP technique, the two pulses vanish simultaneously while maintaining a constant finite ratio of amplitudes.
Coherent creation of ground molecular BECs from atomic BECs [12-19], leads to dynamics described by a nonlinear Schrödinger equation. Recently, nonlinear stimulated Raman adiabatic passage technique (NL-STIRAP) has been implemented in order to population transfer in nonlinear quantum systems [12, 14, 20, 21]. However, with similar conditions with respect to linear counterparts, the NL-STIRAP needs very large Rabi pulse areas which maybe hard to achieve experimentally [12, 14, 17].
Dorier et al. [22] have established a nonlinear stimulated Raman exact passage (NL-STIREP) technique using resonance-locked inverse engineering in a three-level Λ system featuring second and third order nonlinearities. In their method, there is no need for adiabatic passage conditions because the obtained solutions are exact. In comparison with NL-STIRAP -in which the population transfer efficiency is about 80%- this technique (NL-STIREP) allows an efficient and robust population transfer with Rabi pulse areas comparable to the ones of their linear counterpart. In NL-STIREP technique, the peak value of the Rabi frequency, associated to the second-order nonlinearity, is only a few times larger than its linear counterpart and the third-order nonlinearities are dynamically compensated by choosing the suitable detunings, which is considered as resonance-locked inverse engineering.
In this paper, we adapt the proposed technique in [22] to different target states in a three-level Λ system. We shoe that, the relevant design of the pulses, we reach to nonlinear fractional stimulated Raman exact passage (NLF-STIREP). In the following we study numerically robustness of the system with respect to variations in the time delay between the pulses and in the exited state decay rate. To compare the advantages of this method over other similar methods, we study the nonlinear fractional stimulated Raman adiabatic passage method (NLF-STIRAP) in a three-level Λ system and calculate the appropriate values of the Rabi frequencies and time delay between the pulses. As an example in a real physical system, we study the creation of 87Rb molecules from 87Rb atoms (atom-molecule Λ systems) with (1/2 1/2) population transfer using NLF-STIREP technique by a resonance-locked inverse engineering procedure. Then, we investigate the robustness of this technique against the variations in the intensity of the Rabi frequencies and in the time delay between the pulses. To implement NLF-STIREP technique in multi-level systems, we extend this technique to the creation of any preselected coherent superposition of the ground states in nonlinear N-pod systems (N ground states coupled to an exited state), in which the second-order nonlinearity appears only on the pump couplings. In the considered system, we impose the N - 1 ground states, which are initially coherently superposed, are coupled to an exited state via N - 1 pump pulses with the same time dependencies and a Stokes pulse couples the exited state to the final ground state. In order to simplify our calculations, we use the useful Morris-Shore (MS) transformation [23-25] to reduce the system with N + 1 states to an effective three-level Λ-like system. We show that, in multi-level quantum systems with the proper pulse design, one can create coherent superposition of all ground states with equal amplitudes.
Our paper is organized as follows. In Sec. 2, we describe NLF-STIREP technique in three-level Λ system. In Sec. 3, we implement NLF-STIRAP in three-level Λ system and compare it with NLF-STIREP. In Sec. 4, we numerically study this technique in a real atom-molecule Λ system and discuss its robustness. Finally, the conclusions and discussions are summarized in Sec. 5.
2. Nonlinear fractional stimulated Raman exact passage (NLF-STIREP) in three-level systems
2.1. The model
Consider the nonlinear three-level Λ system, which is schematically shown in Fig. 1. The excited state 2 is coupled to the ground states |1〉 and |3〉 with the coupling strengths denoted as Ω P and Ω S , respectively. Here, the subscripts P (S) stand for pump (Stokes) and ∆ P,S are the detunings of the fields. In the interaction picture, the Hamiltonian describing the system reads:
where Γ is introduced phenomenologically to simulate the decay of the excited state |2〉, K
i
(i = 1, 2, 3) are Kerr nonlinearities and
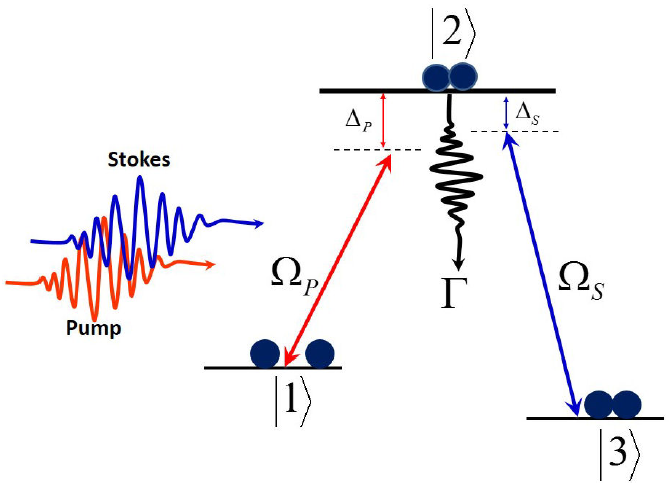
Figure 1 Linkage pattern scheme for the nonlinear three-level system. Ω P , Ω S are the coupling strengths, Δ P;S are the detunings of the fields and Γ is the rate of the spontaneous emission of the excited state (|2〉) out of the system.
The second-order nonlinearity appears via the pump coupling and third-order nonlinearity via the K i terms depending on the population as follows:
in which the K terms are Kerr (third-order) nonlinearities describing elastic collisions between the atom-atom, atom-molecule and molecule-molecule and λ
ij
are constants, act like time-dependent mean-field shifts. Besides, the time-dependent c1 and
In order to keep the mathematics as simple as possible without sacrificing generality, we neglect the nonlinear collisions between particles. Therefore, we consider the model with only second-order nonlinearities (K i = 0). By choosing resonant fields (Δ P,S = 0) and in the absence of exited state decay (Γ = 0), the Eq. (2) is written as follows:
we use general parametrization [22]:
where |Ψ(t)〉 = [c1(t), c2(t), c3(t)] T is the state vector of system. During the time evolution of system, the angle ϕ should be near to zero to prevent the high population transfer in the state |2〉 and the mixing angle θ(t) should dynamically change from θ(t i ) = 0 up to θ(t f ) ≤ (π/2) to lead the population to the state |3〉.
Our goal is to transform the initial state of the system at time t i , |Ψ(t i ) 〉, into the state |Ψ(t f ) 〉 at the end of interaction at the time t f :
Our goal is to transform the initial state of the system at time
where |c 1(t f )|2 + |c 3(t f )|2 = 1. By adjusting θ(t f ), one can create an arbitrary coherent superposition of ground states (|1〉 and |3〉). In order to satisfy this conditions, we generalize angles of Ref. [22] as follows
where T is a normalizing time, t f is the end of interaction time and two constants, η and ϵ, have been introduced such that allow the control of the transient population in the exited and target states. Inserting Eq. (8) into Eq. (5), we obtain the following pulses that describe Rabi frequencies satisfying the conditions of fractional population transfer in our system [22]:
2.2. The numerical study
In this section, our goal is to create coherent superposition of ground states with equal amplitudes. In our method, in order to achieve coherent superposition of ground states, we choose values 0.99 and 0.1 for η and ϵ, respectively. The time delay between the two pulses (τ0) and the pump and the Stokes Rabi frequency amplitudes (max(ΩP), and max(ΩS)) arise automatically from the choice of the parametrization in Eq. (8), but it does not appear explicitly in the equations. The adjustable time delay (τ) can be applied to the angles of Eq. (8) as follows:
Considering the additional time delay between pulses, the Rabi frequencies of Eq. (9) can now be written in an alternative way as follows:
where two constants χP and χS have been introduced to change in the amplitude of the pump and Stokes Rabi frequencies.
Figure 2 represents an example of NLF-STIREP which leads to a coherent superposition of ground states with equal amplitudes (|c1(tf)|2 = | c3(tf)|2 = (1/2)). In the top panel, we plot the corresponding Rabi frequency of the pulses and in the low frame, we show the dynamics of the populations. The Rabi frequencies have a simple and standard form close to Gaussian pulses and similar to the F-STIRAP, the two pulses vanish simultaneously while maintaining finite ratio of amplitudes. The main feature in the procedure of control is its stability with respect to changes in the physical parameters of the system. Therefore, in the following we study these changes and investigate their effects on the robustness of the system. In Fig. 3, the final population |(1/2) - P|3〉| is plotted against the time delay between the pulses τ and to the pump amplitude coefficient (χP) for a fixed Stokes peak coefficient (χST = 1). For sufficiently strong laser pulses, there is an optimal range of τ in which |(1/2) - P|3〉| = 0 is most easily achieved. For example, for a χST = 1 and 0.7 ≥ T ≥ 0.5, acceptable range is 0.15 ≤ τ ≤ 0.9. As shown in Fig. 3, this system is robust with respect to variations of τ and χP. Considering the exited state decay (Γ), the efficiency of population transfer in our system is reduced. In Fig. 4, the final population |(1/2) - P|3〉| is plotted against the exited state decay rate Γ and to the pump Rabi frequency amplitude coefficient, for a fixed Stokes Rabi frequency amplitude coefficient (χS = 1). According to the figure, for Γ = 0 this diagram is in the full agreement with Fig. 2 for a χPT = 1, but with the growing of Γ, in order to achieve fractional population transfer with equal amplitudes (|(1/2) - P|3〉| = 0), we must increase the pump Rabi frequency amplitude coefficient. This system is robust with respect to small variations in the exited state decay Γ, however for sufficiently high decay rates, the efficiency of population transfer decreases considerably.
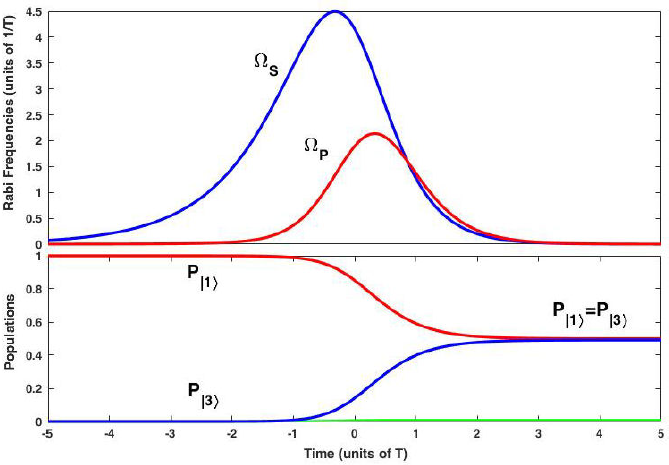
Figure 2 A typical example of NF-STIREP which leads to a coherent superposition of ground states with equal amplitudes for ∈ = 0:1, ƞ = 0:99, Ƭ = 0, Γ = 0, τ 0 = 0:64T, and χP,S = 1 Top frame: Stokes and pump Rabi frequencies, determined by Eq. (11). Bottom frame: Time evolution of the populations.
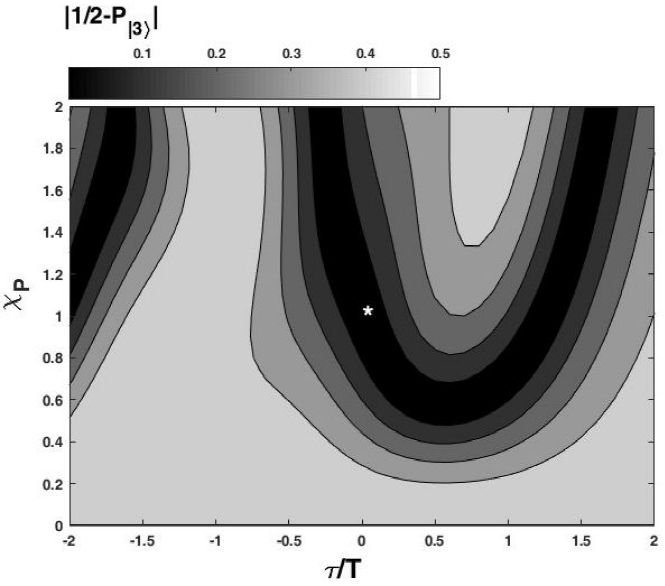
Figure 3 Contour plot at the final time tf of |(1/2) - P|3〉| as function of time delay between the pulses (τ) and to the pump pulse Rabi frequency amplitude coefficient (χP) with χS = 1, in a nonlinear three-level system. Other parameters are as in Fig. 2. The figure represents the robustness of the nonlinear fractional stimulated Raman exact passage in this system. The white star points to the exact solution of the inverse engineering, depicted in Fig. 2.
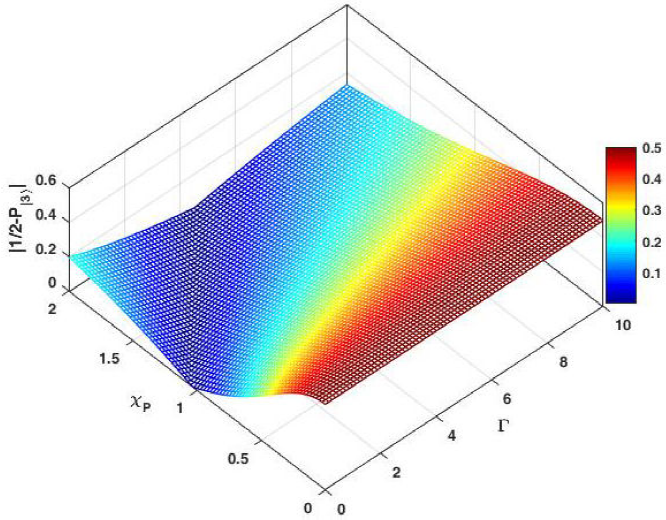
Figure 4 The final population of |(1/2) - P |3〉| as function of the decay rate of the unstable state |2〉 (Γ) and to the pump pulse Rabi frequency amplitude coefficient (χP) with χS = 1, in a nonlinear three-level system. The figure represents the robustness of the nonlinear fractional stimulated Raman exact passage in this system. Other parameters are as in Fig. 2.
3. Nonlinear fractional stimulated Raman adiabatic passage (NLF-STIRAP) in three-level systems
We consider a nonlinear three-level Λ system, depicted in Fig. 1, where |1〉 represents an atomic state and |2〉, |3〉 are the excited and ground diatomic molecular states, respectively. Existence of a coherent population trapping (CPT) state with zero eigenenergy in coupled atom-molecule systems has been reported in several recent experiments [16]. If our system initially prepared in a CPT state, it will stay in the instantaneous CPT state. This is the adiabatic theorem generalized to this nonlinear system. In general, nonlinear systems, because of collisions and intrinsic quantum fluctuations, dynamically unstable regimes appear for the CPT state and adiabaticity will therefore break down [28]. Nevertheless, in our current work, we assume that the system under consideration is always dynamically stable. Setting c2 = 0 in Eq. (5b) and combining it with the total particle number conservation (|c10|2 + |c30|2 = 1)leads to the following CPT population distribution:
where N is normalization factor and |Ψ0(t)〉 = [c1 0, c20, c30]T is the corresponding state vector of system in CPT state. In order to achieve fractional population transfer with equal amplitudes in this system, we impose ΩS(tf) = |c10(tf)|ΩP (tf) in the CPT stat (Eq. 12b). Using Eq. (12) and after the simple algebra yields:
where β is a mixing angle. Without loss of generality, we assume that the coupling strengths ΩP,S are real and positive. We use three equal-amplitude Gaussian pulses, a pump pulse and two Stokes pulses first with the same time dependence as the pump pulse and latter coming earlier as follows [29]:
where T is the duration of each pulse, and τ is the time delay between the pulses. A typical example of time evolution in NLF-STIRAP is shown in Fig. 5. The pulse shapes are defined by Eq. (14) with τ = 0.64T, Ω0T = 20 and β = arctan(√2). The population evolves from state |1〉 (ground state) to the coherent superposition (1 / √2) (|1〉 + |3〉), very similar to the standard F-STIRAP. Comparing Fig. 2 and Fig. 5, we find out, the NLF-STIREP technique can guide the dynamics of the system as efficiently as a NLF-STIRAP, but with considerably smaller Rabi frequency amplitudes. For example in the NLF-STIRAP, Ω0 ≈ (20/T) is required to get about the same high transfer efficiency to the target states and low transient population to the exited state as NLF-STIREP with ΩPmax ≈ (2/T ) and ΩPmax ≈ (4.5/T).
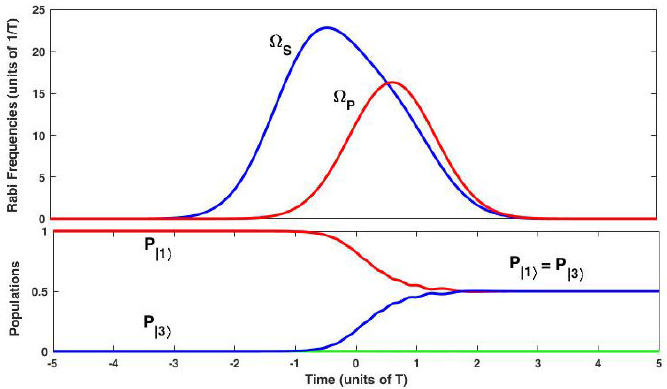
Figure 5 A typical example of NLF-STIRAP in three-level system in the resonance case (∆ = 0) for τ = 0.64T, Ω0T = 20, and β = arctan (√2). Upper: Stokes and pump Rabi frequencies, determined by Eq. (14). Lower: Time evolution of the populations that leads to coherent superposition of atomic and molecular ground states with final equal amplitudes.
4. Nonlinear fractional stimulated Raman exact passage (NLF-STIREP) in a real physical system
In order to perform a numerical study in a real physical system, we consider a pair of 87Rb atoms in state |1〉 wich is photoassociated by a pump laser field of molecular Rabi frequency Ω’P (t) into a molecule in exited state |2〉, which is subsequently driven into a ground molecular state |3〉 by a Stokes laser field of molecular Rabi frequency Ω’S(t). The nonlinear collisions between particles are important in the ultracold quantum atomic or molecular systems (atomic BECs and ground molecular BECs) [30-32]. Here, we use Eq. (2) for this system with considering third-order nonlinearities (Ki) and off-resonant fields (ΔP,S ≠ 0) in the presence of the exited state decay (Γ) in which ΩP (t) = Ω’P (t) √n, ΩS (t) √n, ΩS (t), and n is condensate density [33]. Since the Kerr nonlinearities cause unstable regions in the parameter space [15, 34], to avoid it, we have to consider the phase γ(t) in Eq. (6) as follows:
We see that setting γ˙ = K1 and using resonance locking conditions [22], one can rewrite Eq. () as Eq. () with the inclusion of exited state decay where, Kerr terms have been compensated by detunings. Our goal is to show that, the NLF-STIREP technique can be implemented in the ultracold quantum atomic or molecular systems to transfer the population from the atomic condensate directly to the molecular condensate with equal amplitudes using counterintuitively ordered pump and Stokes pulses [see Eq. (11)]. Our results can be best understood with reference to Table I which gives the values of typical NLF-STIREP with ((1/2) : (1/2) population transfer parameters characteristic of a condensate of 87Rb atoms [13, 35]. Using the values of the parameters in Table I, and an optimum values ϵ = 0.1, η = 0.99, we can achieve almost 98% efficiency of fractional conversion of atomic BECs into molecular BECs, even including the exited state (|2〉) spontaneous emission [see Fig. 6]. In this figure, the atom-ground molecule conversion efficiency is defined as fraction of the initial number of atoms converted into molecules as follows:
where n1 is the initial number of atoms and n3(∞) is the final number of molecules. Figure 7 represents the final population P|3〉 as function of time delay between the pulses (τ) with ϵ = 0.1, η = 0.99. Other parameter values are as in Table I. This figure shows that NLF-STIREP technique is robust against moderate variations of in the time delay between pulses, but the efficiency of population transfer decreases considerably by reducing the coefficient of Rabi frequency amplitudes. For instance, with |τ| ≤ 0.7T and χP = χS = 250 the efficiency of fractional conversion from atomic BECs into molecular BECs is approximately 98%, but with a decrease in the coefficient of Rabi frequency amplitudes down to χP = χS = 25, conversion efficiency also declines to 18%. However, the obtained solutions are exact and there is no need for adiabatic conditions, but the adiabatic passage conditions still exist (χP T, χST >>1).
Table I Typical parameter values and mean-field interaction potentials for efficient fractional stimulated Raman exact passage in rubidium condensates.
| Γ | 3.7 × 107 s-1 | Decay of the quasibound molecule. |
| T | 3.1 × 10-5 s | Pulse duration |
| ΧP | 250 | Coefficient of pump Rabi frequency amplitude. |
| ΧS | 250 | Coefficient of Stokes Rabi frequency amplitude. |
| λ11 | 21328 s-1 | Atom-atom elastic interactions. |
| λ33 | 10664 s-1 | Molecule-molecule elastic interactions. |
| λ13 = λ31 | -27692 s-1 | Atom-molecule elastic interactions. |
| λ2i | 0 | Other elastic interactions. |
| n | 4.3 × 1020 m-3 | Condensate density. |
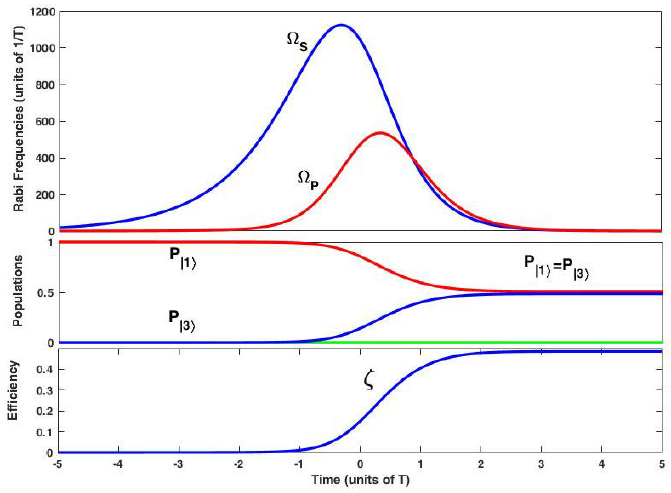
Figure 6 NLF-STIREP in 87Rb atom-molecule Λ system for ∈ = 0.1, η = 0.99, τ = 0, and τ0 = .64T. Other parameters are defined in Table I. Upper : Stokes and pump Rabi frequencies, determined by Eq. (11). Middle : Time evolution of the populations that leads to coherent superposition of atomic and molecular ground states with equal amplitudes. Lower : Time evolution of conversion efficiency ζ (16).
5. Conclusion and discussion
We can generalize, in principle, our approach to the nonlinear N-pod systems. This opens up the search for new schemes for various configurations based on NLF-STIREP and NLF-STIRAP. Figure 8 a) features the linkage pattern of these systems, where N - 1 ground states, which are initially coherently superposed, are coupled to an excited state via N - 1 pump pulses with the same time dependencies and a Stokes pulse couples the excited state to the final ground state. Without taking into consideration of the Kerr terms (third-order nonlinearity) and the exited state decay, the second-order nonlinearity appears only on the pump couplings. Following the MS transformation, one can then find a basis that decouples N - 2 ground states from the others [36-38] [see Fig. 8b)]. If the initial state is coherently superposed, using the following pulses, one can create coherent superposition of all ground states with equal amplitudes.
where
Figure 9 shows an example of such a superposition in nonlinear penta-pod system with equal amplitudes in which, all applied pulses are on exact resonance with their transitions. The initial and final states of the system are:
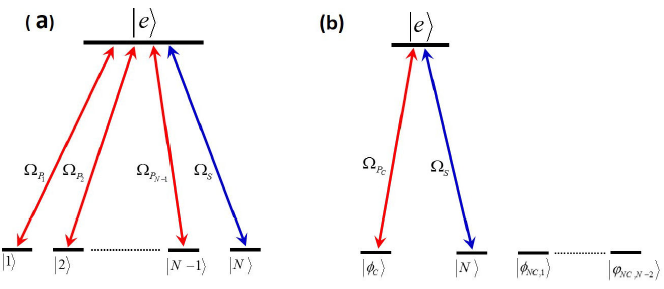
Figure 8 (a) Linkage pattern of the nonlinear N-pod system. (b) Linkage pattern of the nonlinear N-pod system in the MS basis.
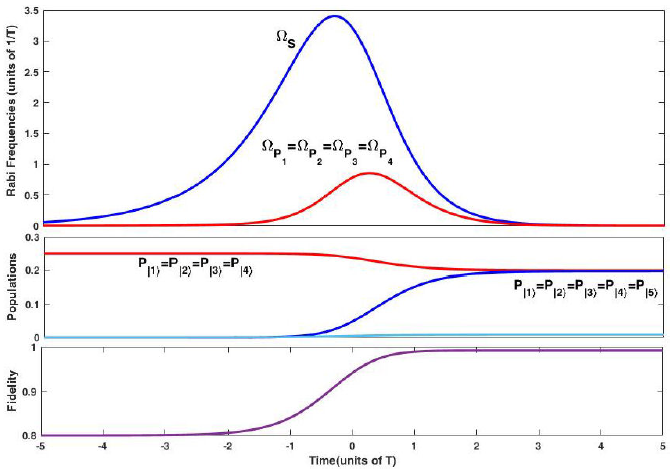
Figure 9 NLF-STIREP in a penta-pod system (N = 5) with ∈ = .1, η = .99, τ = 0, Γ = 0, τ0 = 0.64T, and χP,S = 1. Upper : Stokes and pump Rabi frequencies, determined by Eq. (17). Middle : Time evolution of the populations that lead to the coherent superposition of ground states with equal amplitudes. Lower : Dynamics of the fidelity of the desired state ((19b)).
In conclusion, we have studied fractional population transfer in nonlinear three-level Λ systems using the NLF-STIREP and NLF-STIRAP techniques. We have calculated numerically with the appropriate design of Rabi frequencies, one can then achieve population transfer from an initial state to a desired superposition of all ground states. We have also shown numerically, our system is robust with respect to the exited state decay. However, for sufficiently high decay rates, the efficiency of population transfer decreases considerably. Using numerical comparison, we have shown that the population transfer efficiency in the NLF-STIREP technique can be as efficiently as a NLF-STIRAP, but with considerably smaller Rabi frequency amplitudes. We have used the NLF-STIREP technique to convert the 87Rb atoms into the 87Rb molecules fractionally. We have shown that, with the proper and effective values of time delay between the pulses and Rabi frequency amplitudes, efficiency of fractional converting atomic BECs into molecular BECs is approximately 98%. Although, the efficiency of population transfer significantly decreases by decreasing the laser pulse amplitudes and increasing the time delay between the pulses.











 nueva página del texto (beta)
nueva página del texto (beta)



