1.Introduction
Quantum gases are macroscopic quantum many-body systems that represent a unique scenario to study quantum phenomena such as superfluidity and macroscopic quantum excitations [1]. Moreover, ultracold atoms have emerged as ideal quantum simulators of many-body phenomena, becoming effective testbeds of quantum Hamiltonians. Indeed, the combination of ultracold atoms and optical potentials has opened up a new way of studying condensed matter problems with unprecedented clarity [2]. This is possible thanks to the high level of controllability that quantum gases offer. The dimensionality and geometry of the system can be precisely modified by tailoring trapping potentials with laser light and magnetic fields. The thermodynamic properties of the gas, such as density, temperature, and volume can be easily manipulated. Full control of interparticle interactions is possible via magnetic Feshbach resonances [3]. Even the quantum statistics of the system can be changed by choosing fermionic or bosonic atoms. These are very powerful tools that distinguish ultracold atomic gases from ordinary condensed matter systems.
At ultralow temperatures, diluted gases composed of alkali-metal atoms interact
predominantly through the
The case of ultracold identical fermions is strikingly different. In this case,
However, it is possible to introduce interactions into the system by creating a
two-component spin mixture since Pauli blocking occurs only between identical
fermions, while atoms in different spin states still interact via
A very important consequence of having such control on interatomic interactions is
the possibility of creating different types of bound states among the atoms. For
repulsive interactions,
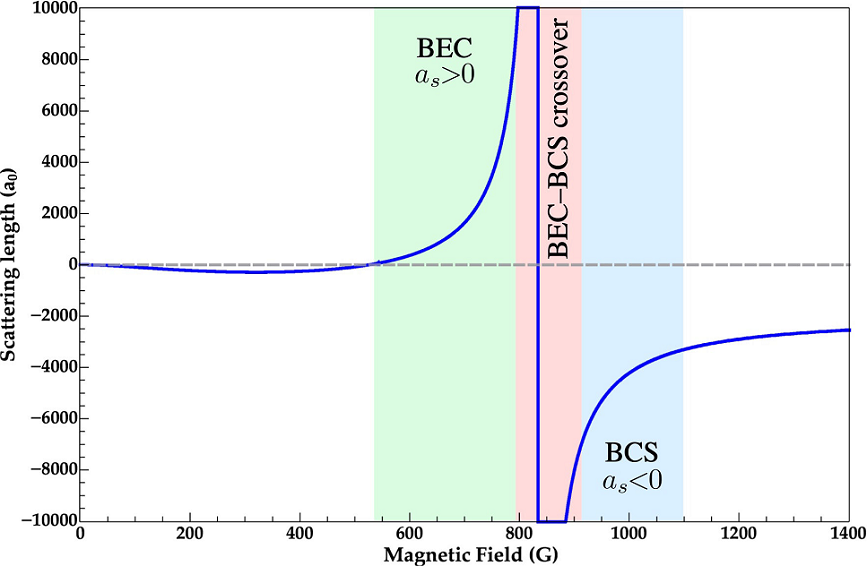
Figure 1 Feshbach resonance for the two lowest hyperfine Zeeman levels of 6Li. Different superfluid regimes are possible depending on the value of the scattering length a s .
In this paper we describe our newly built setup to produce ultracold atomic gases
composed by fermionic 6Li atoms in a balanced spin-mixture of the states
The article is divided as follows. In Sec. 2 we provide details of our experimental setup, this includes the ultra-high vacuum system, the laser system, the magnetic field generation system, and the creation of conservative potentials. Section 3 is devoted to the procedures used to cool down the gas to quantum degeneracy: laser cooling and evaporative cooling techniques, as well as details on the production of a superfluid sample in different interacting regimes. Finally, in Sec. 4, we present our conclusions and future perspectives.
2.1.The ultra-high vacuum system
Our ultra-high vaccum (UHV) system is divided in three main sections, namely (i) the effusive oven; (ii) the differential pumping stage, and (iii) the Zeeman slower system and the main chamber where the sample is produced and the experiments performed. Each of these sections is pumped by a 200 l/s pumping system composed by a combination of an ion pump and a non-evaporable getter (model NEXTorr D 200-5 from SAES getters Inc.). Figure 2 shows a scheme of our UHV, including a detailed cut of our main chamber.
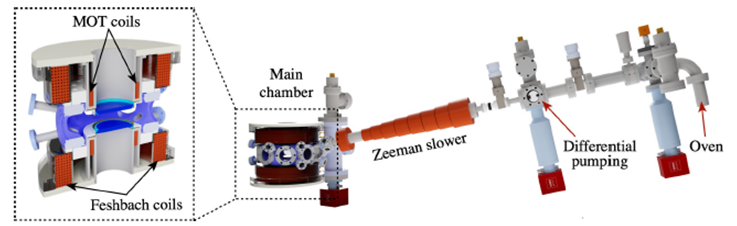
Figure 2 Scheme of the ultra-high vacuum system including the Zeeman and the Feshbach coil systems. On the left we show a cut of the main chamber, exhibiting the distribution of the Feshbach and MOT coils. See text for details.
The effusive oven consists of a cylindrical recipient which contains 5gr of purified
6Li. The oven is heated to a temperature of 450oC, at this
temperature the vapor pressure of lithium is about
The pressure right after the nozzle reaches a value well above
The main chamber is connected to the differential pumping stage by a 56cm long and 16.5 mm inner diameter tube. Around this tube there is a conical solenoid which is used to create a spatially inhomogeneous magnetic field which is required to implement a Zeeman slower system (more details are provided in Sec. 2.3.1.).
Finally, the main chamber is a stainless steel cus- tom-made octagon chamber from Kimball Physics Inc. This chamber contains eight CF40 viewports on its sides; two CF100 vertical viewports, and ten CF16 viewports connected to the chamber by arms extruded from it at an angle of 13o from the horizontal plane. The Zeeman slower tube is connected to the main chamber by one of these arms while the Zeeman slower laser beam enters through another one diametrically opposed with respect to the center of the chamber. All viewports have anti-reflection coating for all the wavelengths used in our experiment (532nm, 671nm and 1064nm).
We have placed on both CF100 flanges reentrant viewports of high optical quality whose inner face is very close to the atoms, at a distance of only half an inch. This opens the possibility of building a large numerical aperture optical system to produce high resolution images of the sample.
2.2.Laser system
2.2.1.Optical cooling scheme
To implement the different laser cooling techniques in our experiment we use
both the
In the experiment, the
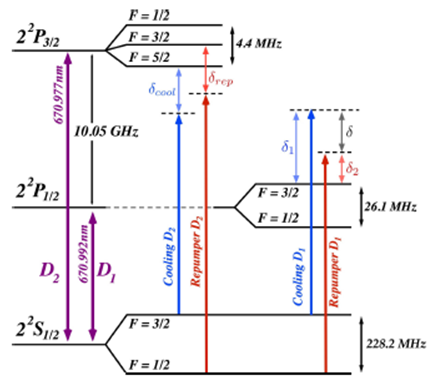
Figure 3 Level scheme (not to scale) for 6Li showing (left) the D 2 and (right) the D 1 hyperfine structures and the transitions used for the laser cooling processes. See text for details.
To produce the
On the other hand, to implement the
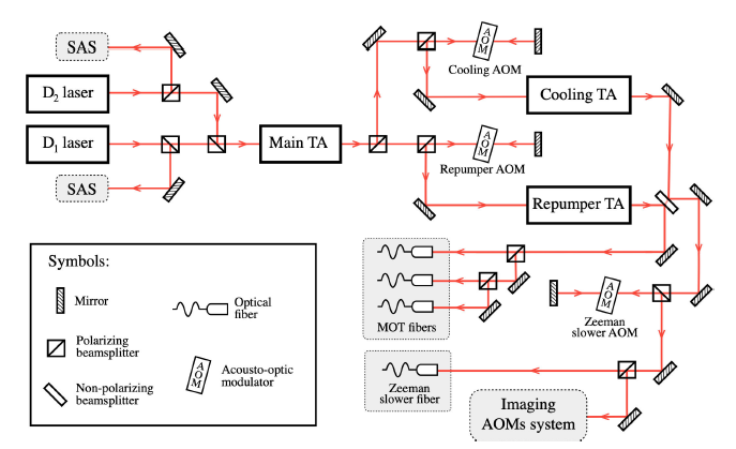
Figure 4 Simplified scheme of the laser cooling and imaging optical setup showing the main features of the system. Lenses and waveplates have been omitted for clarity. See text for details.
As can be seen, we essentially set all the required frequencies using three
AOMs in double-pass configuration [26]. These AOMs are also used to dynamically
change the frequency of these beams and implement the
2.2.2.Generation of probing light
The most important diagnostic tool in cold atoms experiments is imaging the samples using laser light. In our case the preferred technique is absorption imaging due to its simplicity and reliability (27),(28).
Absorption imaging consists in probing the sample using a collimated laser
beam whose frequency is resonant to some atomic transition. To produce the
image, we pulse this light on the atoms during a short time (of the order of
In our experiment we want to produce samples at different interaction regimes across the BEC-BCS crossover. This is done by applying an external magnetic field that changes the value of the scattering length by means of a Feshbach resonance. This magnetic field, in turn, will also cause a Zeeman splitting on the electronic levels of the atoms. Hence, probing the atoms at different interaction regimes poses the necessity of generating different light frequencies to keep the imaging light resonant with the atoms.
To do so, we use the Zeeman slower beam which already has a considerable
shift of
Finally, it is important to mention that the magnetic field used to access
the BEC-BCS crossover is high enough to ensure that the hyperfine splitting
of the atoms is well within the Paschen-Back regime, where the separation
between the
2.3.Magnetic field generation system
We employ three different sets of coils to generate all the required magnetic fields to trap and manipulate the atoms. We describe each of them in the following sections.
2.3.1.Zeeman slower magnetic field
We use a Zeeman slower stage to decelerate the atomic beam coming out from
the effusive oven. As mentioned in the previous section, the detuning of the
Zeeman slower laser beam is
where
The mean velocity of the atoms coming out from the oven is
The magnetic field of the slower is generated by a succession of eight
size-decreasing coils connected in series and an extra ninth coil at the end
of the slower in which the current circulates in opposite direction,
inverting in this way the direction of the magnetic field. This is known as
“spin-flip configuration” [30, 31]. All nine coils are wound directly onto the
slower UHV tube using 1mm diameter cooper wire. The coils are held together
using a thermal conducting and electric insulating ceramic epoxy
(DuralcoTM 128). The total current passing through each coil
is of the order of 2.0A to generate a field which goes from a maximum around
Figure 5a) shows a scheme of the coil configuration of our Zeeman slower. Figure 5b) presents the generated magnetic field. Finally, Figure 5c) exhibits the calculated velocity profile of the decelerated atoms through their propagation along the slower.
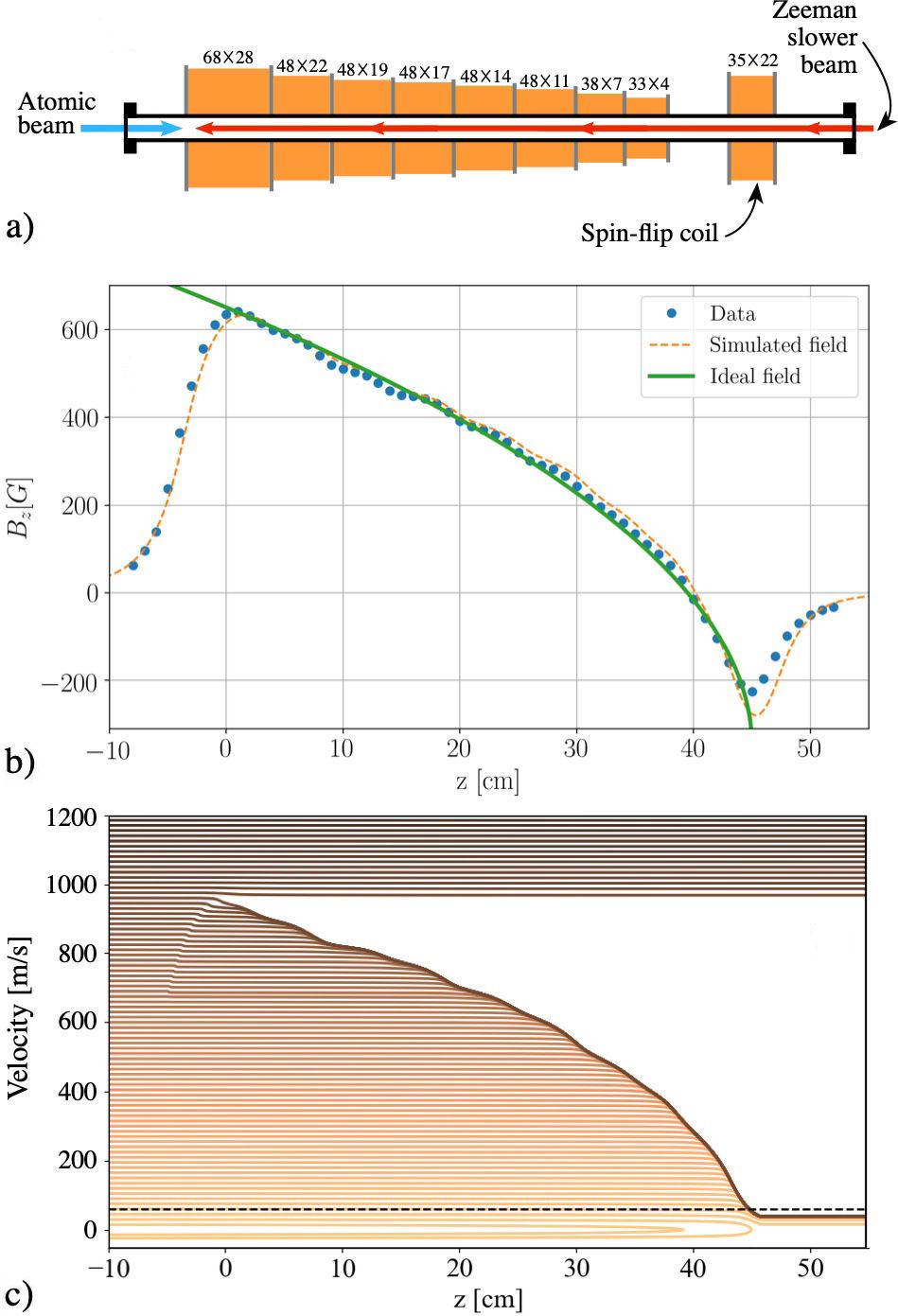
Figure 5 a) Scheme of the coils of our Zeeman slower, the number of windings of each coil is indicated in the format H x V , where V denotes the number of layers in the vertical direction and H provides the number of turns in each layer. b) Axial component of the magnetic field generated along the Zeeman slower, the blue dots are the experimental data, the orange dashed line is the simulated field for this coil configuration and the solid green curve is the ideal magnetic field obtained through Eq. (1). The data uncertainty is of 1% however the corresponding error bars are not visible at this scale. c) Evolution of the speed of the atoms propagating through the Zeeman slower, the dashed horizontal line indicates the capture velocity of the MOT.
2.3.2.Magnetic quadrupole
To produce the magneto-optical trap we use a quadrupole magnetic field whose
axial gradient at the center of the trap is
2.3.3.Feshbach resonance magnetic field
As already mentioned, one of the important advantages of ultracold lithium
gases is the possibility of controlling interatomic interactions with a high
degree of precision by means of a Feshbach resonance [3]. [6]Li presents several Feshbach resonances whose
characteristics depend on the internal state of the interacting atomic pair.
We will use the resonance between states
The Feshbach coils are made by 4mm square section copper wire. This wire is
hollow, with an internal diameter of 2mm, which allows cooling the coil by
circulating cold water inside the wire. These coils were fabricated by the
company Oswald Elektromotoren GmbH and each of them is embedded in an
insulating resin that avoids the induction of undesired eddy currents. We
can circulate a current above 200 A without noticing any significant heating
of the coils. This thermal stability together with a PID feedback loop makes
possible to produce magnetic fields with a stability of one part in
2.4.Conservative trapping potential
We produce the quantum degenerate fermionic system in a conservative trap generated by the combination of an optical potential and a magnetic curvature.
The optical potential consists in a far red-detuned single-beam optical dipole
trap (ODT) created by focusing a gaussian infrared laser beam [20]. We use a single mode
ytterbium-doped fiber laser from IPG Photonics Corp. (model YLR-200-LP) which
delivers up to 200W of continuum linearly polarized infrared light at
Next, we collimate the beam at a diameter of approximately
The trap frequencies of this single beam ODT along the radial and axial directions are given, respectively, by [20]
where
where
This trap provides a tight confinement along the radial direction of the beam,
however, along the axial (or propagation) direction it is very weak. For
instance, at the end of the evaporative cooling where the power of the ODT laser
is approximately
For this reason, we add to the optical potential a magnetic curvature that provides a better confinement along the axial direction. As mentioned in Sec. 2.3.3, we produce such curvature by setting the Feshbach coils slightly off the Helmholtz configuration. In this way, we create a saddle-point magnetic potential of the form [28, 32]
where the trap frequencies are determined by the curvature of the field component
along the corresponding direction, i.e.
Note from Eq. (4) that along the radial direction we have an “anti-curvature” which will tend to deconfine the atoms along that direction. The total frequencies of our hybrid trap will be given simply by
In our experiment, once the quantum sample is produced, we have that the radial
optical confinement is much larger than the magnetic one (
The axial curvature generated for the fields used to access the BEC-BCS crossover
is of the order of
3.Methods and results
In the following sections we provide details on the experimental procedures employed to produce the ultracold samples.
In a very general way, the production of the quantum sample can be divided into two main processes: (i) an initial laser cooling stage mediated by absorption and reemission of light, explained in Sec. 3.1, and (ii) transference into a conservative potential and cooling by forced evaporation, presented in Sec. 3.2
3.1.Implementation of laser cooling technique
In this first cooling process we are able to produce atomic samples at
temperatures as low as 40
3.1.1.Zeeman slower and magneto-optical trapping
Zeeman slower operation
The quantum sample generation process starts by heating the lithium sample
contained in the oven of our UHV system to 450oC . This generates
a high temperature atomic beam that propagates through the UHV system
towards the main chamber. The atoms of this beam undergo a first cooling
process as they are decelerated by our Zeeman slower. Along the slower, a
laser beam propagates in the opposite direction to the atomic beam. This
laser carries two different frequencies, both of them red-detuned by 76
We found that controlling independently the electric current of the spin-flip coil provides better results. Best results are obtained using a current of 2.0A for the spin-flip coil and 2.9A for all other coils, which optimize the number of loaded atoms into the MOT and minimize the corresponding loading time.
Loading of the magneto-optical trap: The decelerated atoms
arrive into the main chamber where we capture them and further cool them in
a magneto-optical trap (MOT) [19]. To implement the MOT we use three retroreflected
mutually perpendicular laser beams with a diameter of
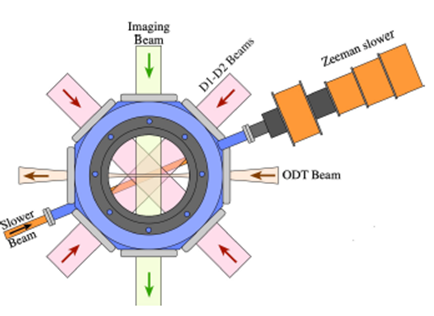
Figure 6 Top view scheme of the main chamber, showing the configuration of the MOT beams (D1 and D2 beams), the imaging beam, the Zeeman slower beam and the ODT beam. MOT and Feshbach coils were omitted for clarity. The third pair of MOT beams is perpendicular to the plane of this scheme and, hence, not shown.
The MOT beams carry two frequencies: a cooling frequency, red-detuned from
the
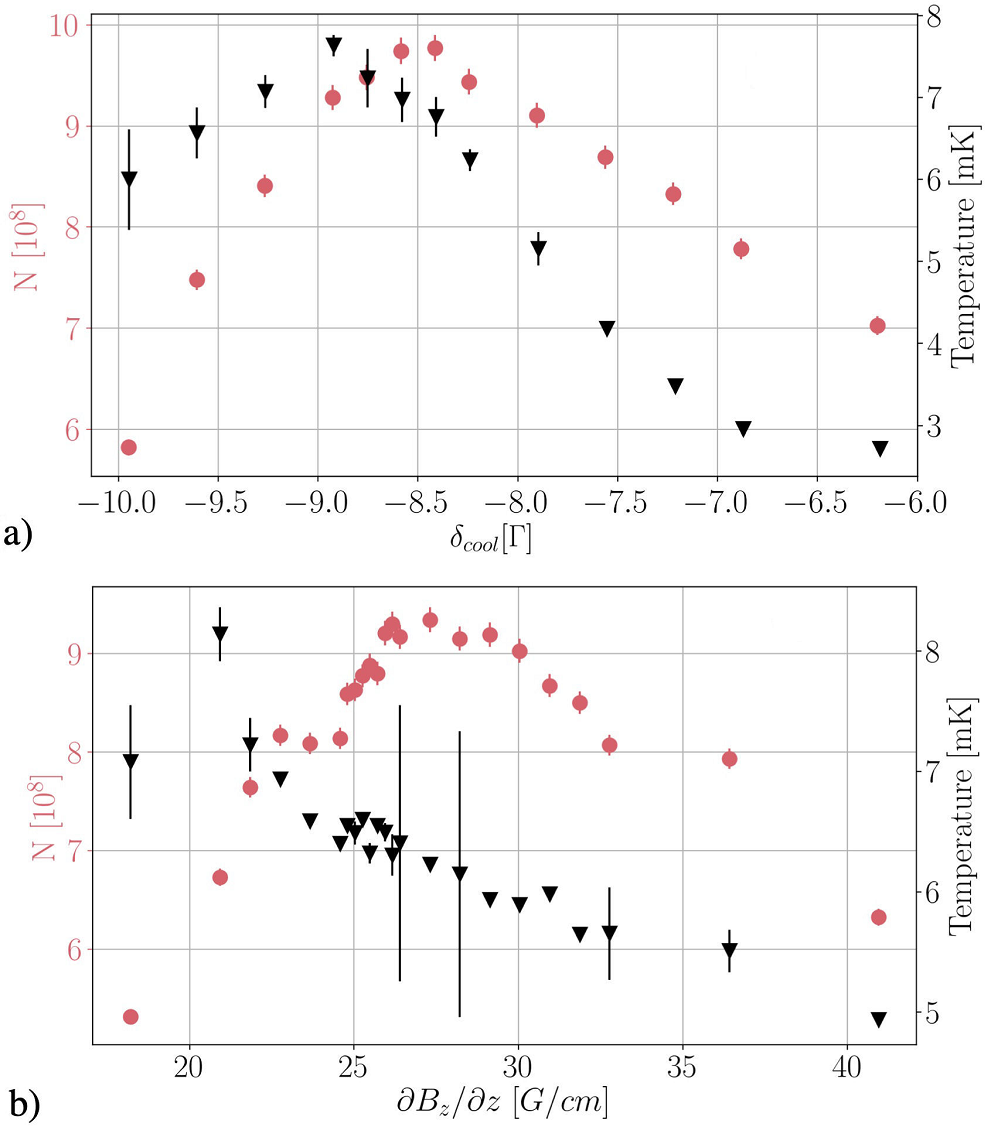
Figure 7 Number of atoms N (red dots) and temperature T (black triangles) of the atoms of the MOT as a function of (a) the detuning of the cooling light and (b) the axial gradient of the quadrupole magnetic field. In these plots, the error bars correspond to one standard deviation of ten independent measurements.
The power of each MOT beam is about
As a result, after a loading time of 8.6s we manage to capture up to
3.1.2.Doppler and sub-Doppler cooling
In order to further cool down the sample and increase its phase space
density, the gas undergoes two different additional laser cooling processes.
We first apply an optical molasses cooling process based on the
D2 optical molasses cooling: The theoretical Doppler
temperature limit for our sample is given by
After loading the MOT we abruptly switch off the quadrupole magnetic field
(we also switch off the Zeeman slower magnetic field 400ms before to
guarantee the absence of any magnetic field in the sample region).
Simultaneously, we decrease the intensity of the MOT beams and shift the
value of cooling and repumper frequencies towards resonance. Figure 8a) shows the effect on
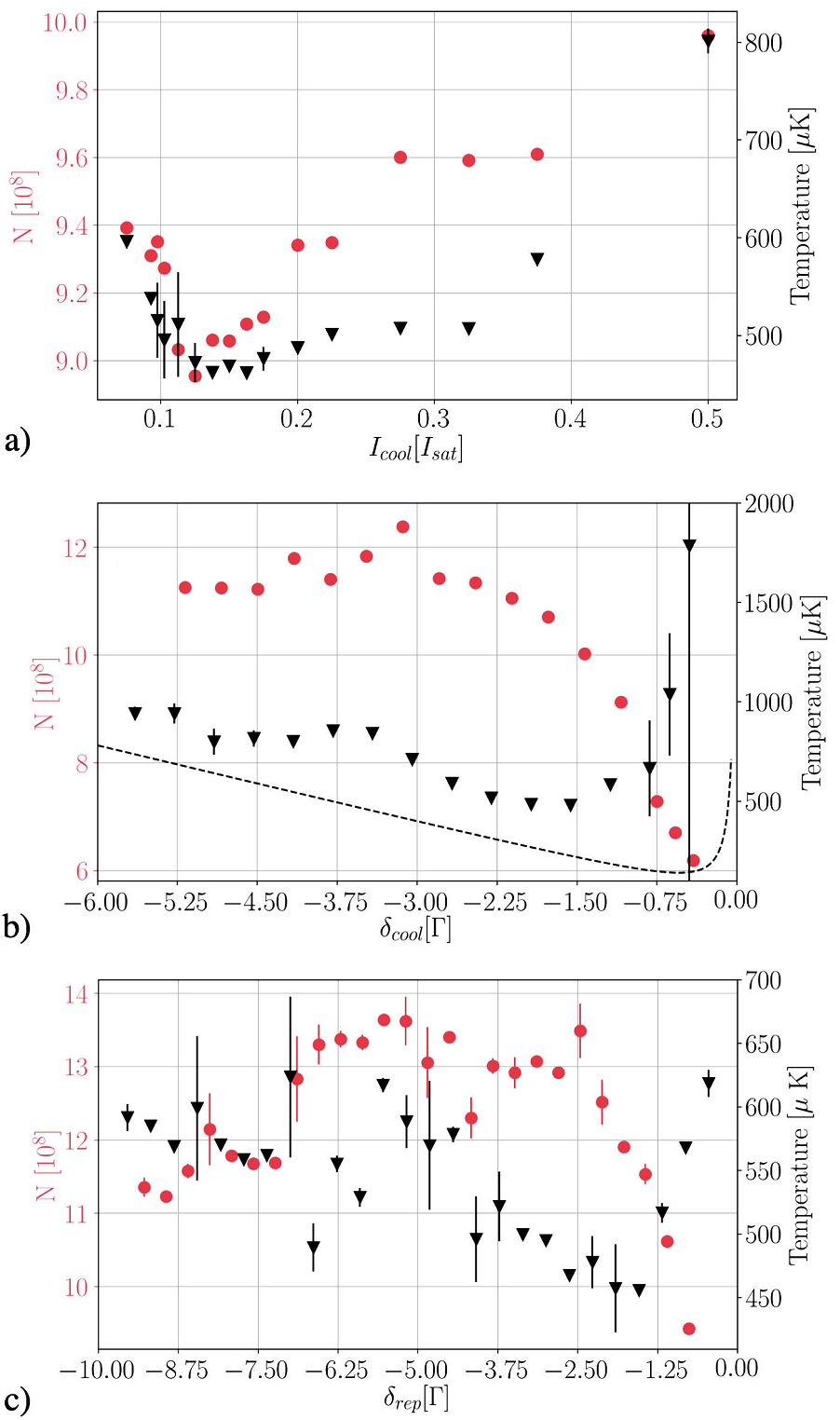
Figure 8 Number of atoms N (red dots) and temperature T (black triangles) of the atoms of the MOT after the D2 optical molasses as a function of a) the intensity of the cooling light and the detuning of b) the cooling light and c) the repumper light. The dashed black curve in b) corresponds to the theoretical Doppler limit for the temperature of our sample. In these plots, the error bars correspond to one standard deviation of ten independent measurements.
As we can see, an important temperature drop is observed when the intensity
of the light decreases. Concerning the frequency shift, as long as we keep
the detuning below
Under these conditions, we are able to cool down about
D1 gray molasses sub-Doppler cooling: Gray-molasses cooling is a
two-photon process in
On the other hand, the
In our experiment, we implement this cooling stage immediately after the
To characterize the gray-molasses we start by fixing
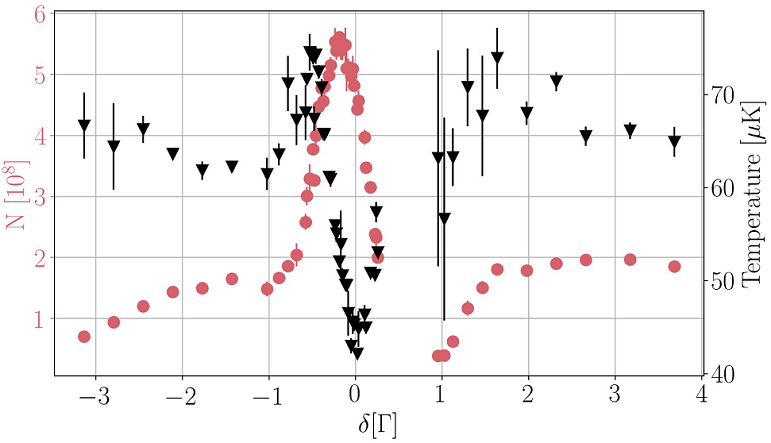
Figure 9 Number of atoms (red dots) and temperature (black triangles) of the sample as a function of the detuning between cooling and repumper light during gray molasses sub-Doppler cooling stage. The error bars correspond to one standard deviation of ten independent measurements.
We can see that the temperature follows a Fano-like profile, reaching a
minimum at
We also measure the effect of changing the cooling detuning
The duration of the gray molasses is also an important parameter. We observe
that after 400
For the next stages, it is important to have all the atoms of the sample in
the
To summarize, after the whole laser cooling process, we are able to produce a
sample containing about
Table I presents the list of all the parameters employed in the laser cooling process.
Table I Optimized parameters of the optical cooling stages
| Cooling stage | Parameter | Optimal Value |
|---|---|---|
| ∂Bz(z)/ ∂z|z=0 | 28 G/cm | |
| δ cool | -8.6 Γ | |
| δ rep | -8.4 Γ | |
| MOT | Loading time | 8.6 s |
| N | 5 x 109 atoms | |
| T | 7mK | |
| PSD | 4.7 x 10-8 | |
| δ cool | -2 Γ | |
| δ rep | -2 Γ | |
| I cool |
|
|
| I rep |
|
|
| D2 Morasses | Duration | 850μs |
| N | 6 x 108 atoms | |
| T | 500 μK | |
| PSD | 1 x 10-7 | |
| δ 1 | +5.7 Γ | |
| δ 2 | +5.7 Γ | |
| I cool |
|
|
| I rep |
|
|
| D1 Gray molasses | Duration | 1 ms |
| N | 4.5 x 108 atoms | |
| T | 40μK | |
| PSD | 6.6 x 10-6 |
3.2.Cooling the sample to quantum degeneracy
After the
3.2.1.Transference into the conservative trap
As explained in Sec. 2.4, our trap is created as the composition of a single-beam optical dipole trap and a magnetic curvature, which provide, respectively, radial and axial confinement.
During the
When the magnetic field is ramped up, the
The Feshbach field curvature provides an axial harmonic confinement of about
After the optical and magnetic fields have been ramped up, we trap about
3.2.2.Evaporative cooling
Evaporative cooling is performed by ramping down the ODT power while keeping
the magnetic field at 832G. To achieve runaway evaporation it is fundamental
that the collision rate does not decrease as the atoms are evaporated, this
means that the density of the cloud needs to increase as its temperature is
reduced. To guarantee this condition, the evaporation process must be
performed slow enough for thermalization to occur. At the same time, the
evaporation has to be the main loss process, so it cannot be too slow for
the background-vapor collisions with the sample to be important. A good
quantity to evaluate the effectiveness of the evaporation process is the
phase space density,
The evaporative process is performed by concatenating three exponential
ramps, as shown in the blue curves of Fig.
11. The first ramp goes from 160W to 35W in 300ms having a
characteristic time of
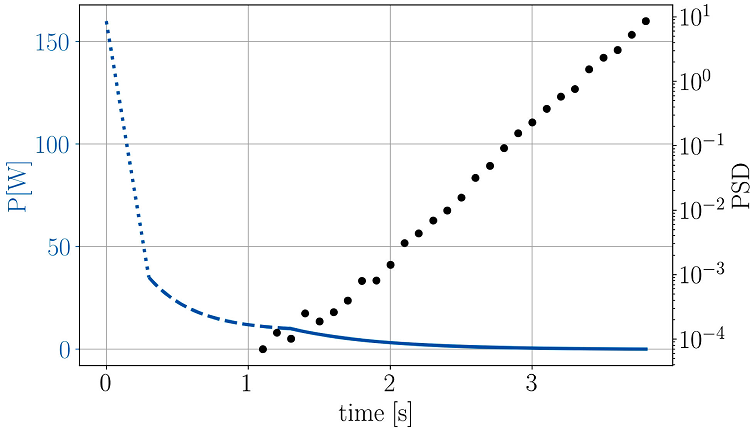
Figure 11 Blue curves: Plot of the evaporation ramps performed by decreasing the power of the optical dipole trap (not a measurement), see text for details. Black data points: Measurement of the phase space density of the system during evaporation. For these measurements, the uncertainty is of the order of 10%, corresponding to one standard deviation of ten independent measurements, however, the error bars are not visible at the scale of the graph.
At the end of the third evaporation ramp we adiabatically ramp the Feshbach field to the corresponding value in order to produce a sample in any desired interaction regime across the Feshbach resonance; this magnetic ramp lasts about 300ms. The regimes that we are interested in exploring are within the interval of 670 to 900G, which contains the BEC-BCS crossover.
By changing the value of the Feshbach field, we also modify the curvature of the magnetic field; however, it changes less than a 10% within the mentioned interval of interest, which means that we do not significantly modify the geometry of the trap as we change the scattering length. Of course, as can be seen from Eq. (5), the frequencies of the trap depend on the power of the ODT, which in turn, determines the temperature and degree of degeneracy of the sample.
After the evaporative cooling process we are able to produce quantum
degenerate superfluid samples containing about
3.2.3.Superfluids across the BEC-BCS crossover
As mentioned in the previous section, we select the interacting regime of the
produced sample at the end of the last evaporation ramp by means of the
Feshbach resonance that allows us to set the value of the scattering length
Evidently, the most important point here is to achieve, at every interacting
regime, temperatures that are below the critical superfluid temperature,
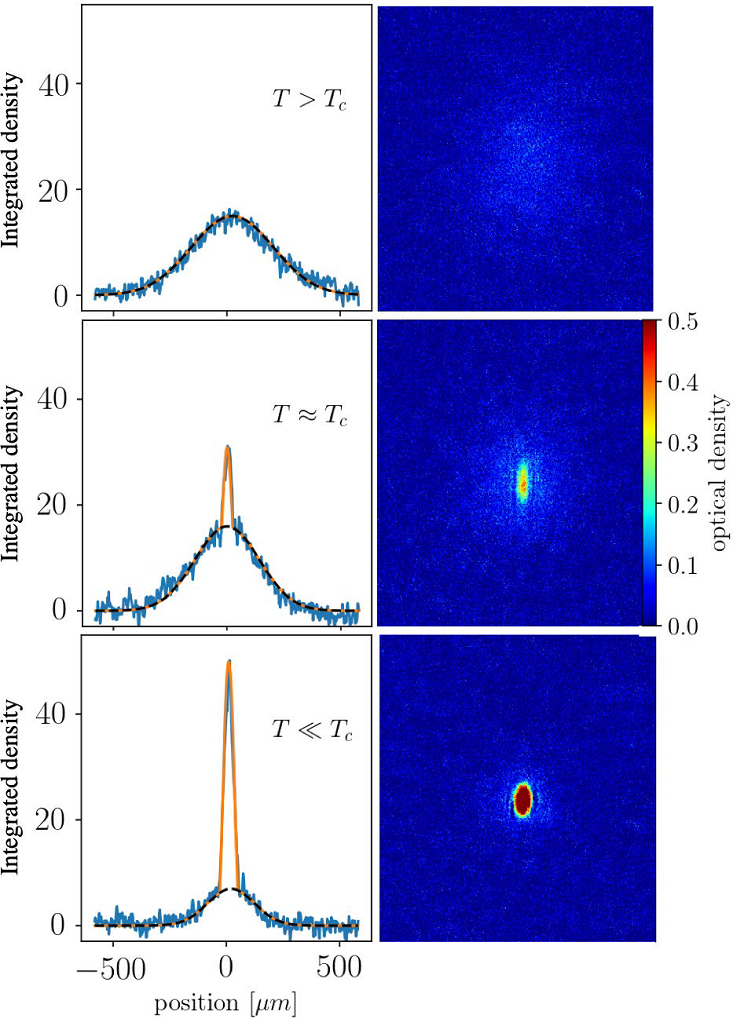
Figure 12 Absorption images of the atomic samples (right pictures) and their corresponding integrated density profile (left graphs) as temperature is decreased. Upper panels: thermal gas above critical temperature T C . Middle panels: gas just below the critical temperature, notice the bimodal gaussian-parabolic distribution. Lower panels: molecular Bose-Einstein condensate well below the critical temperature, the parabolic distribution is dominant and the gaussian one is barely noticeable. The color gradient corresponds to the optical density of the gas. All pictures were taken after a time-of-flight of 15 ms. In the graphs, the dashed black line corresponds to a fitting of only the gaussian wings, while the orange solid line to the bimodal distribution.
As the scattering length increases, within the BEC-BCS crossover range, and
specially right at unitarity, this well defined bimodal distribution starts
to wash out and becomes broader due to strong interactions [4, 41-43]. In this regime, it is not possible to
discriminate between the superfluid fraction and the thermal fraction, and
the density profile looks nearly Gaussian. However, we know that we are in
the superfluid regime due to the following consideration. On the vicinity of
the unitary limit the critical temperature is given by
In contrast, on the BCS side of the crossover, the critical temperature is given by [4, 45]:
so it exponentially decays as the quantity
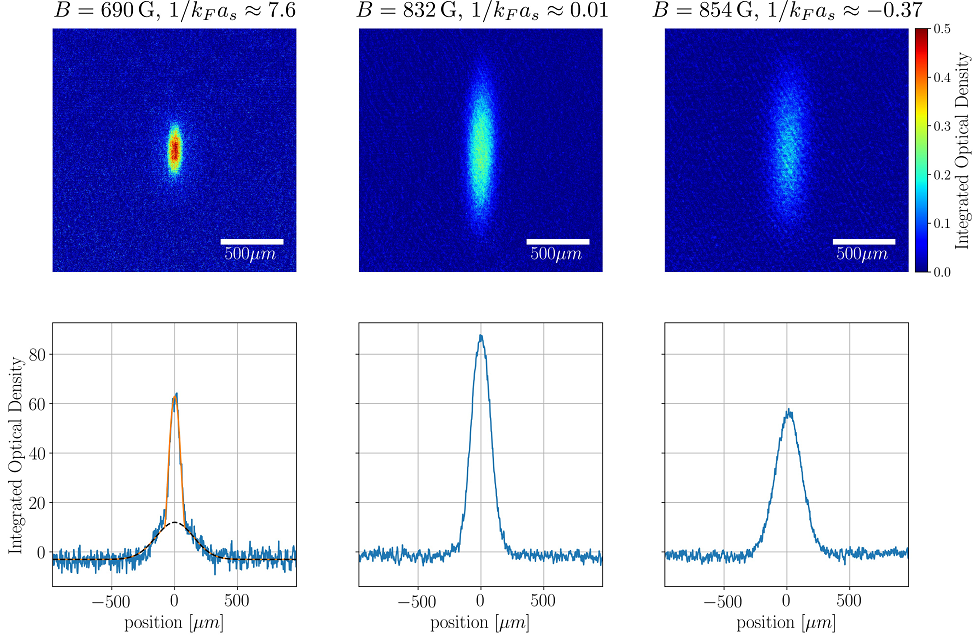
Figure 13 Absorption images of quantum degenerate atomic samples (upper pictures) and their corresponding integrated density profile (lower graphs) as the scattering length is varied across the BEC-BCS crossover. Left panels: Bose-Einstein condensate of molecules at (k F a s ) -1 ≈ 7:6, the bimodal and gaussian fits are shown as a solid orange and black dashed lines, respectively. Middle panels: superfluid gas at unitarity at (k F a s ) -1 ≈ 0:01. Right panels: ultracold gas at the BCS side of the Feshbach resonance at at (k F a s )-1 ≈ -0:37. The color gradient corresponds to the optical density of the gas. All pictures were taken after a time-of-flight of 20 ms.
Besides the considerations concerning the critical temperature that we have presented here, we have also performed an additional measurement that ensures that all the observed regimes present superfluidity. Right after releasing the atoms from the trap, we have performed a fast Feshbach magnetic field ramp from the strongly interacting regimes into the deep BEC side [46, 47]. As result of this ramp, the many-body wave function of the system is projected onto the far BEC side of the resonance. In all cases we observe the characteristic BEC bimodal distribution in the density profile, indicating that at unitarity and its vicinity we always have condensation of atomic pairs.
4.Conclusion and Future Perspectives
We have presented the experimental setup and methods we use to produce and study
ultracold fermionic superfluid samples of 6Li. We are able to generate
samples containing
As a future perspective, we plan to study topological and hydrodynamic excitations such as quantized vortices (see for instance [48, 49] and references therein). We specifically want to understand how the dynamics of these systems depend on the interacting regime as well as on the temperature of the cloud. To carry out these experiments, we need to expand the capabilities of our imaging system. In particular, as a complementary technique to our current absorption imaging system, we will implement the non-destructive phase contrast imaging technique [27] that will allow us to perform several images of the same sample without perturbing it. This is very important to address the dynamics of the superfluid sample.
As a long term perspective, we plan to produce ultracold samples of 7Li, a
bosonic stable isotope of lithium. This is possible because we have also placed
purified 7Li in our oven. The optical frequencies of the











 nueva página del texto (beta)
nueva página del texto (beta)



