1.Introduction

In the initial stage of photosynthesis, light is absorbed by pigment-protein complexes (PPC) and the electronic excitation energy is transfered to a reaction center (RC), where a charge separation reaction occurs ¹.

Green sulfur bacteria is a photosynthetic organism whose light harvesting complex is composed of a chlorosome antenna anchored to aggregates of a protein called Fenna-Matthews-Olson complex (FMO) ², ³. The FMO complex serves as a quantum wire that delivers electronic energy from the chlorosome to the RC with a quantum efficiency close to 100% ⁴.

The FMO complex is a trimeric protein of identical subunits which function independently of each other. Subunits of the FMO complex consist of two 𝛽 sheets that form a hydrophobic pocket which holds 7 strongly coupled pigment molecules, called chromophores or bacteriochlorophylls a (BChla) ², ³.

Quantum coherence can be used as an operational resource to acomplish tasks that would not be possible by classical means ⁵-⁷. Ultrafast two-dimensional electronic spectroscopic experiments have revealed that during energy transport the FMO complex sustains electronic coherence between the seven chromophores. Coherence lasts for at least 300 fs at room temperature, long enough to impact energy transfer dynamics ⁸-¹⁰. In the FMO protein, the functional role of coherence manifests in an interplay between coherent dynamics of the system and incoherent effects of environment that assists quantum transport efficiency ^{4 11}-¹⁴. Subsequent two-dimensional electronic spectroscopy experiments ¹⁵, ¹⁶ and a theoretical examination ¹⁷ demonstrate that the excitation coherently moves through two alternative energy transfer pathways depending on the site that is initially excited.

Quantum correlations between different parts of a system are a true signature of their non-classical nature. Quantum discord is a quantifier of quantum correlations that includes entanglement as a subset and is more robust than entanglement against environment influences ^{19 20}. Quantum discord can be exploited as a useful resource to perform tasks in manners that are classically impossible like the implementation of quantum computation and quantum communication protocols ²¹-²⁶.

Investigations in the energy transfer dynamics of the FMO complex have revealed the existence of bipartite and global entanglement between the electronic states of spatially separated chromophores ¹⁴, ²⁷-³¹. These studies of excitation dynamics in the FMO protein show that entanglement lasts for 1-2 ps under Markovian models and for over 4 ps under more accurate non-Markovian models. According to the authors, the fact that the entanglement lifetime is comparable with the timescale of energy transfer in the FMO complex, a few picoseconds, suggests that quantum correlations may benefit excitation transport. Interestingly, quantum discord between pairs of chromophores lives for longer times than entanglement ²⁹. A functional role for quantum correlations in pigment-protein complexes is consistent with coherence enhancing properties of energy transport like efficiency or robustness ^{4 11}-¹⁴. We believe that the results of recent research where it is demonstrated that entanglement is maximum along the two electronic energy transfer pathways also support the idea of a functional role for quantum correlations ³²-³⁴. Three investigations have studied the role that non-classical correlations between chromophores play in energy transmission efficiency: two of them ³⁵, ³⁶ did not find any conclusive results and the third ³⁷, with positive results, was subject to harsh criticism from the group who first quantified entanglement in the FMO protein ³⁰.

The minimum quantum contribution to the uncertainty associated to the measurement of composite systems with local observables is known as local quantum uncertainty (LQU) . Recently, it has been proved that LQU meets the criteria for a discord-like quantifier of quantum correlations. The LQU approach has been used as a reliable measure to characterize nonclassical correlations in a few frameworks ³⁴-⁴⁴

The general motivation for studying coherence and quantum correlations in light-harvesting structures is that the precise characterization of these quantum resources is essential, on the one hand, for understanding their functional relation with the energy transfer mechanism and, on ther other, to be able to construct naturally robust quantum devices based on that mechanics. Our principal aim is to demonstrate that the Local Quantum Uncertainty is a highly flexible, robust, and consistent metric to characterize quantum correlations, which is and a novel approach that had not been studied before. We determine the Local Quantum Uncertainty in subsets of the chromophores network in a Gibbs thermal ensemble because a correct picture of which chromophores remain quantum correlated at long times depends on the thermal equilibrium state reached by the system.

Specifically, we implement the LQU method in subsystems of pure and mixed states represented by the eigenstates and by the thermal equilibrium state determined by the FMO Hamiltonian from Chlorobium tepidum. Remarkable advantages of the LQU approach discussed in this work over other methods are: LQU is a discord-like quantifier of quantum correlations so it is more general than the entanglement based techniques, LQU is easier to calculate than direct definition of quantum discord, the LQU approach can be readily implemented in dynamical systems, and the LQU method flexibility allows to describe the sets with the strongest non-classical associations in qubits networks. The identification of the strongest associations as subsystems of three sites serves to investigate whether it is possible to relate quantum correlations with energy transport pathways. Finally, we take the LQU of the most quantum correlated subsets of chromophores as the signature of the non-classicity of the system to study physical properties such as populations, energy fluctuations, and specific heat. This analysis shows that the availibility of energy levels determined by increasing temperature dictates the relation between a measurable macroscopic magnitude and non-classical resources.

This paper is organized as follows: Sec. 2 describes the quantum states that emerge from the excitonic Hamiltonian of the FMO complex; Sec. 3 describes the aspect of quantum coherence that defines it as a quantifiable resource to be consumed in quantum information protocols; Sec. 4 develops the LQU method of quantifying quantum correlations in a chromophores network; Sec. 5 shows results of LQU, concurrence and coherence in subsystems of pure and mixed states of the FMO complex; finally, in section 6 we present an overview of the implementation of the LQU approach: usefulness, advantages, limitations and scope.

2.Model for the FMO complex chromophores network

The FMO protein is a trimer constituted of three identical monomers which function independently. For this reason, we focused on electronic energy transfer (EET) in only one of the monomers. Each monomer has a 7 chromophores network embedded in its structure. In the network, wave functions of the chromophores are distant enough from each other to overlap.

The electronic state of chromophore m goes from its ground state |mg⟩ to the first excited electronic state |me⟩ when it absorbs a photon from the light-harvesting complex. EET through the chromophores network takes place one excitation at the time so we use the site basis {|m⟩} with m=1,…,7 𝑚=1,...,7:

where the base vector |m⟩ stands for site m in the excited state while the rest of the sites are in the ground state. The molecular state represented by |m⟩ is called a site exciton. Thus, the excitonic Hamiltonian H is expressed as:

where site energies E_m are the optical transition energies for each site and interaction terms V _nm of energy transfer correspond to dipole-dipole electric interactions between pairs of site excitons.

Adolphs and Renger ⁴⁵ calculated individual excitation energies E_m running a genetic algorithm that takes site energies as parameters that are optimized to fit experimental linear absorption spectra and linear and circular dichroism; interaction terms V _nm were calculated using structural data from the FMO protein crystal.

We find the delocalized exciton eigenstates {|M⟩} and energy eigenvalues {εM} by solving the Hamiltonian eigenvalue equation:

with 𝑀=1,...,7. Eigenstates {|M⟩} are a quantum superposition of site excitons:

where cmM is the probability amplitude associated to eigenstate |M⟩ for site m to be in the excited state. Each eigenstate {|M⟩} has associated a density matrix {ρM} whose representation in the site basis reads:

where the density matrix elements of the eigenstates are:

and the superindex M indicates the eigenstate they belong to.

If the system is in thermal equilibrium the mixed state can be written as:

ρt=1Zexp⁡-βH=1Z∑Mexp⁡-βεMMM=∑mnλmntmn

where Z=tr{exp-βH} is the partition function, β=1/kBT is the thermal energy factor and:

are the density matrix elements when the state is spanned in terms of the site basis.

3.Coherence as a quantifiable resource

In quantum information science, coherence is used as a resource that is consumed to perform tasks that are not possible by classical means. The resource theory for coherence interprets physical laws as constraints on the set of free quantum operations to be implemented on quantum states. If a coherent state is the resource to be consumed then the set of free quantum operations are incoherent operations and the available free states are incoherent states. A proper measure of coherence C must fulfill the following conditions: C(ρ) = 0 when ρ is a incoherent state, C does not increase under incoherent operations (monotonicity), C does not increase on average under selective incoherent operations (strong monotonicity), C does not increase under mixing of quantum states (convexity). The l₁ norm of coherence Cl1 ⁵, ⁶ defined by:

fulfills the former conditions so we will use it as a proper measure of coherence. For a d-dimensional Hilbert space with a reference basis {|i⟩}i=0,...,d-1 the maximally coherent state is:

For the state |Ψd⟩ the l₁ norm of coherence Cl1 takes the value: Cl1|Ψd⟩=d-1. We have introduced the quantifiable aspect of coherence to compare it with quantum correlations and to investigate the relation between two different quantum resources.

4.Quantum correlations in C2⊗Cd systems

The first proposals for measuring the non-classical share of correlations were based on the nonseparability of the subsystems states, i.e., quantum entanglement. However, entanglement does not account for all non-classical correlations because separable mixed states usually contain quantum correlations. Quantum discord is a more general quantifier of non-classical correlations than the entanglement based ones ⁴⁸. Quantum discord is based on the idea that by measuring one of the subsystems one can extract the shared classical information. Except for a few simple cases quantum discord is hard to compute, nevertheless a seemingly disadvantageous feature of quantum mechanics (uncertainty) provides an easier method for calculating quantum discord.

There is a close link between quantum-induced uncertainty and quantum correlations that can be exploited to establish a discord-like quantifier of quantum correlations ³⁸. In quantum systems the measurement uncertainty may have classical and quantum contributions. If the state to be measured is incoherent in the observable eigenbasis the measurement output statistics will be classical: measurement of a pure state is completely deterministic and it will exhibit zero variance but for mixed states the contribution to the variance comes from classical uncertainty due to the mixedness of the state. In states displaying coherence, the measurement uncertainty has two contributions, apart from the classical randomness that comes from the mixing, there is a quantum randomness that is intrinsic to coherence. This quantum randomness manifests in the interference pattern of the outcome statistics and is an additional quantum component to the uncertainty.

The quantum contribution to the uncertainty is due to the non-commutativity between the state ρ and the observable K ³⁹. A reliable measure of quantum uncertainty is zero if and only if ρ and K commute (ρ is a eigenstate of K or a mixture of eigenstates of K), does not increase under classical mixing and is equal to the variance for pure states. The Wigner-Yanase skew information I(ρ,K) ⁴⁹, defined by:

fulfills the former conditions so we will use it as a convenient measure of quantum uncertainty.

We have identified the quantum share to the measurement uncertainty and quantified it by a measure of the non-commutativity between the state ρ and the observable K. Now we will proceed to establish the relationship between quantum uncertainty and quantum correlations. In a bipartite system only zero discord states:

can commute with local observables KA⊗IB (vectors {|iA⟩} form an orthonormal basis where K_A is diagonal). If the bipartite system shares non-classical correlations its quantum state does not commute with any local observable KA⊗IB and single observable measurements on A will display an inherent quantum uncertainty. The minimum skew information associated to a local measurement on subsystem A is called local quantum uncertainty (LQU) and will be denoted by U_A(ρ):

where the minimization is over the set of local observables with non-degenerate spectrum. It can be proven that the LQU fulfills the requirements to be a discord-like quantifier of non-classical correlations in bipartite states ³⁸, ³⁹. There is a geometric interpretation of the LQU that suggests a relation with symmetric discord: the LQU is the minimum Hellinger distance between the state ρ before and after a local root-of-unity unitary operator has been applied ³⁸.

To minimize the skew information, the local observable K_A can be parametrized using the Pauli matrices and the identity operator:

where α, β are complex scalars, n⃗ is a unitary vector and σA=(σx,σy,σz)⃗ are the Pauli matrices. Thus, the skew information is:

The advantage of this approach lies in the existence of a closed form to calculate the LQU for bipartite systems where A is a qubit and B a qudit of dimension d (ρ is a state defined on an Hilbert space C2⊗Cd):

where the matrix elements of (WAB)ij are:

Equation (15) involves the maximization of a quadratic form which results in:

where λmaxWAB is the maximum eigenvalue of the matrix (WAB)ij. The closed form (Eq. (16) and Eq. (17)) to calculate LQU between two subsystems where one is a qubit and the other is a qudit is suitable to characterize quantum correlations in qubits networks like the FMO protein.

5.Results

We calculated quantum resources in pure and mixed states of the FMO protein. Pure states are constituted by the eigenstates {|M⟩} of the FMO Hamiltonian; with respect to mixed states, improper mixtures come from subsystems of the eigenstates and statistical mixtures are the thermal equilibrium state and its subsystems.

To demonstrate the advantageous features of the LQU approach we will follow this method: (1) to define families of partitions in the system, (2) to determinate the quantum states and (3) calculate the LQU between subsystems. We choose three three ways to divide the seven chromophores network; each partition defines a family of quantum correlations.

When the system is described by a eigenstate |M⟩ the three families of quantum correlations {f1,f2,f3} were calculated using the density matrices {ρMf1,ρMf2,ρMf3} and if the state is in thermal equilibrium the density matrices corresponding to the three families of quantum correlations are {ρtf1,ρtf2,ρtf3}. The spectral decomposition of the density matrices is:

where the g index specifies if the family of quantum correlations is calculated in a eigenstate (g=M) or in thermal equilibrium (g=t).

To calculate LQU between subsystems we need to obtain the (WAB)ijg,fl matrices, this is accomplished by inserting Eq. (18) in Eq. (16):

Eq. (19) is the general formula that we will use to calculate the three families of quantum correlations in the eigenstates and in thermal equilibrium state.

5.1.Family f1

The first family f₁ corresponds to the LQU between one chromophore {Cr}=Subsystem A1 and the remaining 6 chromophores {Cs,Ct,Cu...}=Subsystem B1 (with s,t,u,...≠r). Correlations from family f₁ display a global perspective on the chromophores individual participation and had not been calculated before. The quantum correlations of family f₁ involve the whole network so the density matrices ρMf1 and ρtf1 correspond to ρM and ρ_t from Eq. (5) and Eq. (7).

In Fig. 1, two histograms show the LQU between Subsystem A ₁ and Subsystem A ₂ for the seven eigenstates {|M⟩} of the FMO Hamiltonian. The information of chromophores C₁,C₂,C₃, and C₄ is in Fig. 1a) and the information of chromophores C₅, C₆, and C₇ is in Fig. 1(b). Fig. 1(a), we see that the eigenstates that contribute the most to the correlation of C₁ and C₂ with the rest of the chromophores network are 3 and 6; and the eigenstates that contribute the most to the correlation of C₃ and C₄ with the rest of the chromophores network are 1 and 2. In Fig. 1b) we see that the eigenstates that participate the most to the LQU of C₅ and C₇ with the rest of the chromophores network are 2, 4, 5, and 7; and the eigenstates 5 and 7 have the highest values of LQU for the correlations between C₆ and the rest of the chromophores network.

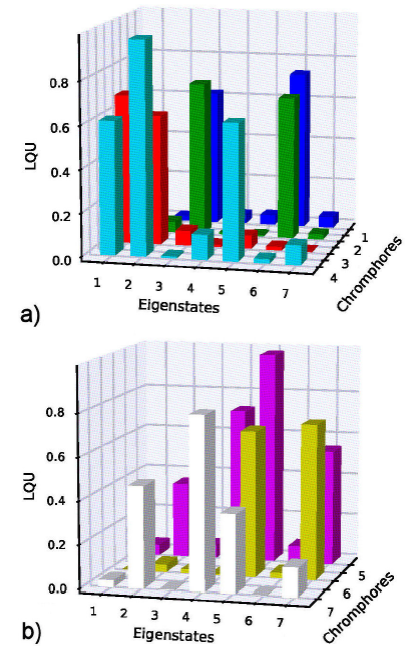
Figure 1 LQU between between one chromophore {Cr} and the remaining 6 chromophores {Cs,Ct,Cu...} for the 7 eigenstates {|M⟩} of the FMO Hamiltonian. (a) r = 1; 2; 3; 4, (b) r = 5; 6; 7. 

The next step is to extend the quantum correlations analysis of pure states, represented by the eigenstates, to the state in thermal equilibrium. In Fig. 2 we show the LQU between individual chromophores Subsystem A ₁ and the remaining 6 chromophores Subsystem B ₁ as a function of temperature for the state in thermal equilibrium. In Fig. 2a) we show the LQU of chromophores C₃ and C₄ with the rest of the chromophores network. At low temperatures, chromophores C₃ and C₄ are the most quantum correlated with the rest of the network. This can be explained if we recall that the eigenstates with the greatest contribution to the LQU between C₃ (or C₄) and the rest of the network are the ground state and the first excited state. In Fig. 2b) we show the LQU of chromophores C₁, C₂, C₅, C₆, and C₇ with the rest of the chromophores network. Regarding the associations of Fig. 2b), the values of LQU are marginal in amplitude and the curves show a local maximum around 100 K. Besides the difference in values of LQU, we separated the associations of family f₁ in two sets because in Fig. 2a) the LQU is a strictly decreasing function while in Fig. 2b) the LQU first decreases, then increases and finally decreases again as the temperature rises. The LQU of the associations in Fig. 2b) takes low values at low energies because the eigenstates 1 and 2 do not have an important participation; as the temperature increases so does the LQU because eigenstates 3, 4, and 5 start to participate. At high temperatures, quantum correlations vanish in Gibbs states because all the eigenstates are equally probable, i.e., the mixedness is maximum and the non-classical correlations are lost.

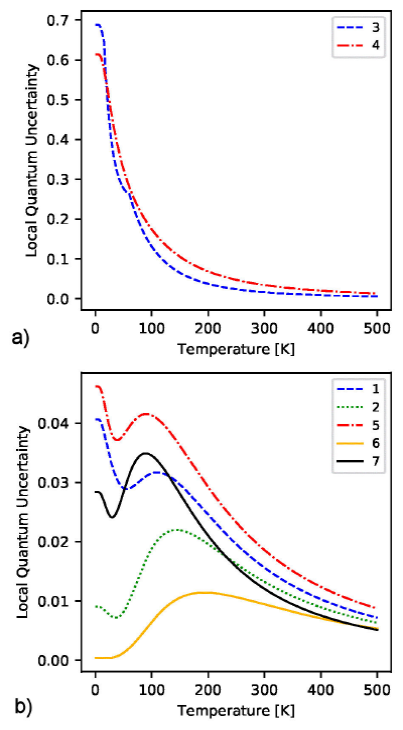
Figure 2 LQU between between one chromophore {Cr} and the remaining 6 chromophores {Cs,Ct,Cu...} for the thermal equilibrium state as a function of temperature. (a) r = 3; 4, (b) r = 1; 2; 5; 6; 7. 

To investigate the relation between two different quantum resources we calculated the quantum coherence of the system and compared it with LQU. In the inset of Fig. 3 we plot the quantum coherence Cl1 of the seven chromophores as a function of temperature for the thermal equilibrium state. As expected, coherence vanishes as the temperature rises. In the main panel of Fig. 3 we use temperature T as parameter to obtain curves of LQU versus coherence Cl1(T),LQU(T). The comparison facilitated by the parametric curves allows to see that the LQU of chromophore C₃ and C₄ is a monotonically increasing function of the coherence. We do not present the corresponding parametric curves for chromophores C₁,C₂,C₅,C₆ or C₇ because they do not have an important global participation.

Figure 3 The main panel shows LQU between between one chromophore {Cr} and the remaining 6 chromophores {Cs,Ct,Cu...} as a function of coherence, with r = 3; 4. The inset shows coherence of the seven chromophores network as a function of temperature for the thermal equilibrium state. 

5.2.Family f2

The second family f₂ accounts for the LQU between chromophore {Cr}=Subsystem A2 and chromophore {Cs}=Subsystem B2 (with r≠s). Family f₂ will serve two purposes: to provide information about the specific associations of chromophores that sustain the quantum correlations defined by family f₁ and to make a comparison with an entanglement quantifier of two qubits.

We determine the quantum correlations defined by family f₂ in subsystems of two chromophores. We calculated the partial trace to the state of the whole system ρg over 5 subsystems to obtain the quantum states of two chromophores: tr5s(ρg)=ρgf2, where the g index specifies if the family of quantum correlations is calculated in a eigenstate (g=M) or in thermal equilibrium (g=t).

First, we examine the associations determined by family f₂ in the lowest eigenstates of the FMO Hamiltonian but in Fig. 4 we only present results from the ground state. For the lowest eigenstates the highest correlation is between chromophores C₃ and C₄. In decreasing order, correlations that also stand out when the system is in the first excited state are: {C7,C3}, {C5,C3}, {C7,C4}, {C7,C5}, and {C5,C4}.

Figure 4 LQU between chromophores {Cr} and {Cs} for the ground state. 

After studying correlations in the eigenstates, we used the thermal state to establish reliability of the LQU approach by comparing it with concurrence (a valid quantifier of entanglement in the two qubit subspace). We calculate concurrence and LQU in all the combinations of pairs of chromophores but only show the pairs with the highest values.

Figure 5a) exhibits LQU curves for the pairs {C3,C4}, {C4,C5}, {C4,C7}, and {C1,C2}; while Fig. 5b) presents the corresponding concurrence curves. In Fig. 5, there is a qualitative and quantitative similarity between LQU and concurrence curves. At low temperatures the LQU between the pair {C3,C4} is an order of magnitude greater than for any other pair. The reason for this is the high value of LQU for both the ground state and the first excited in this pair. This behavior was also present between the subsystems with the highest values of quantum correlations of family f₁.

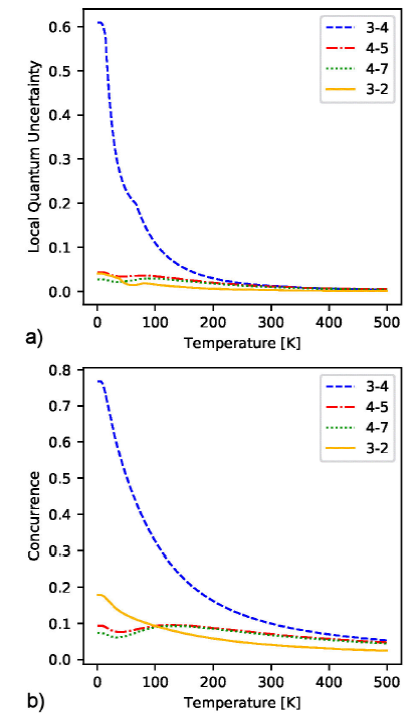
Figure 5.a) LQU and b) concurrence as a function of temperature for chromophore pairs{C₃,C₄}, {C₄,C₅},{C₄,₇} and {C₃,C₂} . 

The rest of the pairs, with weaker contributions to the quantum correlations, also show a qualitative similarity between LQU and concurrence curves. These results confirm that the LQU approach is a reliable method for measuring quantum correlations in subsystems of the FMO complex.

A direct result for any pair of chromophores {C_r,C_s} with quantum state ρgf2 is that the l₁ norm of coherence Cl1(ρgf2) is equal to the concurrence C(ρgf2). To see this, first consider that an X^ matrix reads:

X^=Q1100Q140Q22Q2300Q32Q330Q4100Q44. (20)

There is a direct form of calculating concurrence in X^ density matrices of two qubits ⁵⁰. The concurrence C(X^) is:

CX^=2max⁡0,Q14-Q22Q33Q23-Q11Q44 (21)

This is useful because the quantum state of two chromophores {C_r,C_s} is a X^ matrix:

ρgf2=∑m≠r,sλmmg0000λrrgλrsg00λsrgλssg00000, (22)

where the elements λmng are defined in Eq. (6) and Eq. (7).

In the specific case of two site excitons, the elements {Q₁₂,Q₄₁,Q₄₄} are zero, therefore for any pair of chromophores {C_r, C_s} with quantum state ρgf2 the concurrence is simply:

C(ρgf2)=2|λrsg|. (23)

With the matrix in Eq. (22) we can also express the coherence for the state of two chromophores {C_r,C_s}:

Cl1(ρgf2)=2|λrsg|, (24)

which is equal to the concurrence, as can be seen in Eq. (23).

5.3.Family f3

Now that we have evidence that LQU is a valid quantifier of quantum correlations in subsystems of the FMO complex we search triads of chromophores whose association results in stronger correlations than those found in bipartite systems. To do so, we calculated LQU between one chromophore {Cr}=Subsystem A3 and pairs of chromophores {Cs,Ct}=Subsystem B3 (with s,t≠r). We considered all possible combinations but only present results of selected triads with the following behavior: LQU between Subsystem A ₃ and Subsystem B ₃ is stronger than LQU between {C₃} and any individual chromophore ({C_s} or {C_t}) from Subsystem B ₃. The search and selection of strongly correlated triads of chromophores was accomplished by virtue of the robustness of the LQU approach. In the FMO complex, quantum correlations between Subsystem A ₃ and Subsystem B ₃ had not been calculated before.

We calculated the partial trace to the state of the whole system ρg over 4 subsystems to obtain the quantum states of three chromophores: tr4s(ρg)=ρgf3, where the g index specifies if the family of quantum correlations is calculated in a eigenstate (g=M) or in thermal equilibrium (g=t).

We continue with the analysis in sets of three chromophores considering the eigenstates with lower energy but in Fig. 6 we only present an histogram with results from the ground state. Results show that for both the ground state the sets with the highest values of LQU are chromophore C₄ with the pair {C₃,C₇}, chromophore C₃ with the pair {C₂,C₄}, and chromophore C₄ with the pair {C₃,C₅}.

Figure 6 LQU between chromophores {C_r} and {C_s,C_t} for the ground state. 

After considering the eigenstates we will broaden the analysis to the thermal state. In Fig. 7, we present the selected triads where the LQU between one chromophore Subsystem A ₃ and a pair of chromophores Subsystem B ₃ is function of temperature a) and coherence b). Figure 7 shows the sets of chromophores with the highest values of LQU ({C4,C3,C7}, {C3,C2,C4}, and {C4,C3,C5}). Quantum correlations of the sets in Fig. 7a) are strictly decreasing functions of the temperature. At low temperatures, the LQU of the triads in Fig. 7 is an order of magnitude greater than for the other triads. Again, the reason behind this is the high value of LQU for both the ground state and the first excited in these associations. This behavior was also present in the most quantum correlated associations of chromophores in families f₁ and f₂ and.

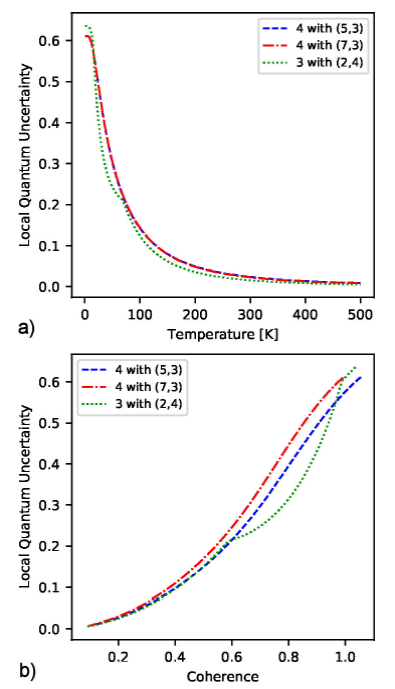
Figure 7 LQU between chromophores {C_r} and {C_s, C_t} for the thermal state as function of a) temperature and b) coherence. 

With respect to the parametric curves of LQU versus coherence, results show that the triads of chromophores with the highest values of LQU, {C₄,C₃,C₇}, {C₃,C₂,C₄}, and {C₄,C₃,C₅}, display a functional relation with their coherence. A monotonically increasing function was also present in the strongest associations of chromophores in families f₁ and f₂.

5.4.Quantum correlated subsets of chromophores in the physical framework of the FMO system in thermal equilibrium

The FMO protein mediates excitation energy transfer between the chlorosomes and the reaction center. Chromophores 3 and 4 are the linker pigments between the FMO complex and the RC. We use the thermodynamic equilibrium state in Eq. (7) to calculate the functional dependence of the populations on the temperature, cf. Fig. 8. At low temperatures and when thermal equilibrium state has been reached, the highest probability is finding the system in the localized excited state |3⟩ followed by |4⟩. As the temperature rises, the seven sites are equally probable to be excited.

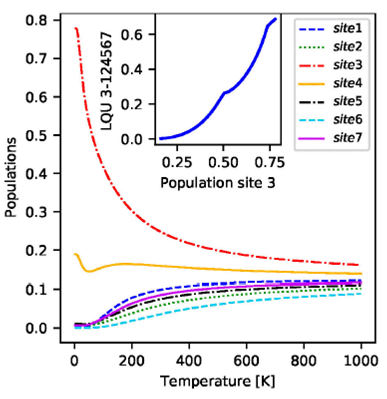
Figure 8 The main panel shows the populations of the seven sites as function of the temperature. The inset shows the LQU between C₃ and the rest of the network as a function of the population of site 3. 

We evaluate the relation between most correlated sets of chromophores and population of site 3, the most probable of the linker pigments to be excited when thermal equilibrium state has been reached. In the inset of Fig. 8 we show a parametric plot of the LQU between site 3 and the rest of the network versus population of site 3, i.e., ρ33(T),LQU(T). These results show a positive correlation between charge at the site that delivers energy to the reaction center and non-classicity, measured by LQU, as a function of the temperature. The relation between linker sites of the transfer network and specific quantum correlations will also be present when analyzing efficient energy transfer pathways.

As an intermediate step, before searching for a relation between non-classicity and a measurable macroscopic magnitude, we evaluate the fluctuation of the energy ⟨ΔH2⟩=⟨H2⟩-⟨H⟩2 in the frame of the canonical ensemble. In the inset of Fig. 9, we plot the functional dependence of statistical variance ⟨ΔH2⟩ on the absolute temperature to show that an indicator of uncertainty associated to the measurement of energy increases with temperature. On account of the increasing temperature and the system losing quantum coherence, the mixedness augments, so the contribution to the variance mostly comes from classical uncertainty.

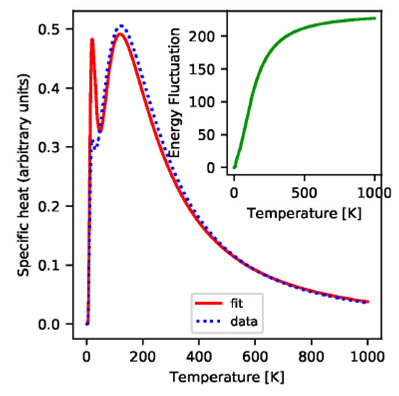
Figure 9 The main panel shows the specific heat at constant volume as function of the temperature. The inset shows the energy fluctuation of the system ⟨H2⟩-⟨H⟩2 as a function of the temperature. 

With this result we can now evaluate the relation between the variance, that accounts for both classical and quantum uncertainty, and the LQU, a quantifier of the quantum contribution to the uncertainty. In the inset of Fig. 10, we show a parametric curve of the fluctuation of the energy versus the LQU of chromophore C₃ with the rest of the network, i.e., LQUT,⟨ΔH2⟩T. We see that as temperature rises, there is an inverse correlation between total uncertainty associated to the measurement of energy and the minimum quantum contribution of the uncertainty. In the inset of Fig. 10, we also show an exponential fit for the energy fluctuation as a function of the LQU: ⟨ΔH2⟩=aexp-bLQU1/2+c. The optimal parameters are a = 327.2, b = 2.0 and c = -71.4. This fit shows the type of functional relation sustained between uncertainty from both quantum and classical sources and the minimum quantum ignorance.

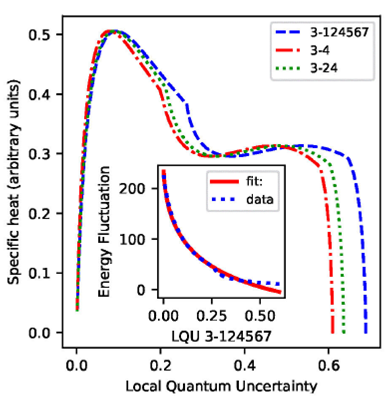
Figure 10 The main panel shows the specific heat at constant volume as function of the LQU associated to the most correlated subsets of chromophores, i.e. C₃ with the rest of the network, C₃ with C₄, and C₃ with {C₂,C₄}. The inset shows the energy fluctuation of the system ⟨H2⟩-⟨H⟩2 as a function of the LQU between C₃ and the rest of the network. 

To evaluate the relation between non-classicity and a measurable macroscopic magnitude we begin by analyzing the functional dependence of the specific heat at constant volume on the temperature Cv=⟨ΔH2⟩/kT2 (Fig. 9). We choose specific heat measurements because they constitute an essential technique for characterizing fundamental excitations involved in phase transitions.

The system presents a Schottky-like anomaly in the specific heat data as a function of temperature. The Schottky anomaly manifests itself as a maximum in the specific heat when the energy gap Δ1=ε1-ε0 of a two-level system is fixed ⁵¹.

A multilevel system might presents multiple peaks in the specific heat that correspond both to the discrete energy gaps Δn=εn-ε0 that become available as temperature increases and to the degeneracy of each energy level ⁵¹.

In a model for a multilevel system in thermal equilibrium with no degeneracies, the specific heat C_v is:

Cv=(Δ1(Δ1-Δ2)+Δ2(Δ2-Δ1)exp(-(Δ2+Δ1)/KT)(KT)2(1+exp(-Δ1/KT)+exp(-Δ2/KT))+exp(-Δ1/KT)(Δ12)+exp(-Δ2/KT)(Δ22)(KT)21+exp(-Δ1/KT)+exp(-Δ2/KT), (25)

where Δ1=ε1-ε0 and Δ2=ε2-ε0. In the FMO Hamiltonian there are no degeneracies so the double peak structure that shows up in the specific heat of Fig. 9 is associated to the energy gaps Δ₁ and Δ₂ becoming accesible.

To investigate the relation between non-classicity and a measurable macroscopic magnitude, in Fig. 10 we present a parametric plot of specific heat versus the LQU of the strongest associations: LQUT,CvT. In Fig. 10, we can clearly see that the double peak structure of the heat capacity is conserved.

The peak in specific heat at the right, associated to the prevalence of the energy levels 𝜀 0 and ε₁, shows that as temperature rises from 0 to ∼ 50 K the LQU is constant, present the highest values, and the specific heat sharply increases from 0 to 0.3. The eigenstate analysis shows that by accesing to the lowest energy levels ε₀ and ε₁, the system presents specific non-classical features with the highest values. Therefore, at low temperatures, the fast increment in the capacity of the system to absorb heat energy is related to the prevalence of specific non-classical correlations. As the temperature increases and LQU decreases from 0.6 to ∼0.3 the specific heat remains constant. The peak in specific heat at the left, associated to the availibility of the energy gap Δ2=ε2-ε0, shows that when the values of LQU are marginal in amplitude (LQU < 0.1) the heat capacity decreases from its maximum value around 0.5 to 0. Therefore, by accesing to higher energy levels, the second peak in the specific heat is not associated to high values of quantum features. The analysis of the parametric plot in Fig. 10. shows that the availability of energy levels determined by increasing temperature dictates the relation between specific heat (a measurable macroscopic magnitude) and LQU (a quantifier of the non-classicity nature of the FMO network).

6.Conclusions

This article presents a systematic LQU based method intended to examine the structure of quantum correlations in pigment-protein complexes. To do so LQU, concurrence, and coherence were computed in subsystems of pure and mixed states of the FMO complex from green sulfur bacteria.

The LQU method consists in selecting families of partitions in the system, determination of the quantum state and calculation of LQU between subsystems. Partitions are selected to define two subsystems where one is a qubit and the other is a qudit (in the FMO complex the qubit corresponds to a single site and the qudit can be any number of sites). Determination of the quantum states is achieved by calculating the corresponding partial trace to the density matrix of the whole system. Calculation of LQU is accomplished by selecting the maximum eigenvalue of a 3 x 3 matrix. The LQU method input is a quantum state of site excitons therefore it can be readily implemented in dynamical models.

To show the versatility of the LQU method, we calculated quantum correlations between subsystems that had never been considered before, i.e., LQU between individual chromophores and the remaining 6 chromophores (family f₁). Correlations from family 𝑓 1 present a global perspective of the chromophores individual participation. Results of family f₁ show that chromophores C₃ and C₄ are the most quantum correlated with the rest of the network. In subsequent partitions, the robustness of the LQU allows us to find the specific associations of chromophores that sustain quantum correlations of chromophores C₃ and C₃.

To validate the LQU as a discord-like quantifier we compared it with a valid entanglement quantifier of two qubits (concurrence). The LQU-concurrence comparison was made using the thermal equilibrium state for all the combinations of two chromophores (family f₂). According to results of family f₂, quantum correlations of chromophores C₃ and C₄ with the rest of the network mainly arise from the following pairs of chromophores:{C₃,C₄},{ C₄,C₅},{C₄.C₇}, and {C₂,C₃}.

LQU between chromophores C₃ and C₄ is an order of magnitude higher than for any other pair but, as the relation between pairs suggests, by adding a specific third site the association strengthens even more. Associations suggested by family f₂ are confirmed by results of family f₃ which show that the most quantum correlated triads are: C₃ with {C₂,C₄}, C₄ with {C₃,C₅}, and C₄ with {C₃,C₇}.

Three additional results were found: (1) By comparing the LQU approach with entanglement based techniques in pairs of chromophores we proved that the former is a valid discord-like quantifier of quantum correlations. (2) When we calculated quantum correlations using the eigenstates we found that some subsystems have high values of LQU in the ground and first excited state. When considering the state of these subsystems in thermal equilibrium we found that they have remarkably high LQU at low temperatures. This relation is present in the three families. (3) A monotonically increasing function between two quantum resources, coherence and quantum correlations, is present in the most correlated associations of families f₁ and f₃. In all associations of family f₂ coherence equals concurrence.

One of the most interesting problems in quantum biology is finding out if quantum correlations in light harvesting complexes play a functional role enhancing energy transport efficiency. Investigations addressing this issue did not find any conclusive results ³⁵, ³⁶ or were subject to criticism ³⁷. In our work, we quantified quantum resources in a system that remains in the same state as time elapses: the system is either in a stationary state or in thermal equilibrium. We did not work with a dynamic model so we cannot directly relate our results with excitation transport efficiency. Nevertheless, there is a previously reported relation between the most quantum correlated subsets of the chromophores network and the two energy transport pathways in the FMO protein (32)-(34).

In the FMO complex, the excitation coherently moves through two alternative energy transfer pathways depending on the site that is initially excited . When chromophore C₁ is the initial excited pigment, the excitation propagates through pathway A: C1→C2→C3→C4 and when the initial excited pigment is chromophore C₆, the excitation is transferred through pathway B: C6→C5,C7→C4→C3. We found that in thermal equilibrium the strongest non-classical associations of chromophores are C₃ with {C₂,C₄} , C₄ with {C₃,C₅}, and C₄ with {C₃,C₇}. The quantum correlation of C₃ with {C₂,C₄} involves chromophores from pathway A: C₃ connects C₂ of the initial stage with C₄ of the final stage. The quantum correlations C₄ with {C₃,C₅} and C₄ with {C₃,C₇} involve chromophores from pathway B: C₄ connects C₅/C₇ of the initial stage with C₃ of the final stage. According to our results, once thermal equilibrium is established, the subsets of chromophores with the strongest quantum correlations are the final stage of the two energy transport pathways in the FMO complex. This analysis shows a possible connection between highly correlated subsets of chromophores and energy transfer pathways.

The relation between strong quantum correlations and energy transport pathways is consistent with previous research of multipartite entanglement in the FMO protein . In our work, we show that the LQU is a promising metric and provides a framework to establish the posible relation of quantum energy transmission with the non-classical correlations in the FMO complex.

The non-classicity of the system, represented by the LQU of the most quantum correlated subsets of chromophores, can be used to analyze physical properties such as populations, energy fluctuations, and specific heat. As the temperature rises, the number of accesible states is increased and the double peak structure that shows up in the specific heat reflects the availability of the energy gaps Δ₁ and Δ₂. The first peak, where the states ε₀ and ε₁ prevail, shows a correspondence between a sharp increase in heat capacity and constant LQU. The second peak, where the states ε_0, ε₁, and ε₂ are available, the quantum signatures of the system are marginal and heat capacity begins to diminish. Thus, the accessibility of energy levels, mapped by the specific heat, defines the relation between a measurable macroscopic magnitude and non-classical resources.

The benefits of the LQU approach over other techniques are: (1) being LQU a discord-like quantifier it is more general than the entanglement based techniques, (2) LQU is easy to compute because the inherent minimization process associated with discord reduces to finding the maximum eigenvalue of a 3 x 3 matrix, (3) LQU permits characterization of correlations that had not been studied before (family f₁ and f₃), (4) the LQU method discloses the strongest associations in qubits networks and (5) the LQU technique can be readily implemented in dynamical systems. The principal limitation of the LQU approach is that it is a bipartite quantifier so it cannot offer a global measure of quantum correlations.

We introduced a quantum information method based on local quantum uncertainty to comprehensively characterize non-classical correlations in subsystems of the FMO complex. Identification of the most quantum correlated subsystems reveals a detailed map of the exceptionally efficient structure of the FMO complex. The study of biological networks has potential applications in engineering and quantum information technology.