1.Introduction
The study of heavy quarkonia in quantum chromodynamics (QCD) is a field theoretical
non-perturbative problem which has promoted the development of several techniques
appropriate to address this issue. Under certain considerations, it can be
simplified to a non-relativistic (NR) quantum mechanical problem by exploring the
interaction strength between quarks inside hadrons in the static limit of the
interaction potential (SLIP) between quarks. Lattice QCD simulations 1,2 suggest for this potential a Coulombic term at
short distances plus a linearly rising part at large inter quark separations, which
to-date has motivated a large number of phenomenological models (3)-(19) that
capture the quantum chromodynamic traits of strong interactions. Whilst the SLIP
picture for light-quarks must be taken with a grain of salt, for the case of heavy
mesons,
The relevant Schrödinger wave equation (SWE) with any of these SLIPs often has to be
solved numerically. To that end, a vast number of numerical strategies have been
implemented in literature among which, to count a few, we find the shooting method
22, the Asymptotic Iteration
Method (AIM) 23 and many others
such as different forms of Runge-Kutta methods. Most numerical strategies
implemented for solving the SWE are as precise as going up to O(d2) of
grid spacing d. The Matrix Numerov Method (MNM) (see, for instance 24) which in the context of meson
physics has been put forward by the Qena group 25 and extended by our group 26, departs from a discretization of the kinetic
term in the SWE in such a manner that the problem of solving the radial SWE is cast
in the form of a matrix eigenvalue problem. In this form, its accuracy is of
O(d6). On the other hand, many proposals of quark model (QM)
potentials have used quark masses far higher than those reported in the Particle
Data Booklet in various years 3-19. The quark model community has exploited the freedom in
choosing quark masses (the so called constituent quark masses) and quark interaction
energy (QIE) parameters in
In our present work we study the spectrum of heavy
After preparing the firm ground from MNM we obtain the charmonium and bottomonium spin averaged masses and radii, in order to circumvent the struggle for numerical accuracy in the numerical solution, we introduce a variatonal approach combining the Heisenberg uncertainty principle and the variational principle in the Hamiltonian of the SWE. Such an approach, which we refer to simply as the variational principle (VP), imposes an algebraic transcendental relation between the masses and the radii of these states and is partially based in our previous work in 26. The results from our VP are less uncertain than those from MNM. In the remaining part of this article we present the details as follows: Section 2 introduces MNM to solve the SWE. Section 3 presents our model of the quark velocities, and the decay widths for different decay modes of spin averaged S-states of charmonia, and bottomonia. In Sec. 4 we develop a strategy of combining the variation in mesonic Hamiltonian with Heisenberg UP through our momentum width-model to establish analytical relation between spin averaged masses and radii of heavy meson states. Conclusion and further possible developments are discussed in Sec. 5. In the Appendix A to this paper we have calculated spin averaged masses by including hyperfine, spin-orbit, and tensor interactions to SL potential and compare these against the spin averaged masses in Tables I and II obtained without these spin effects while in Appendix B we have estimated the bare quark masses. The color screening is explored in Appendix C.
Table I Masses [GeV] for c
| nL | Exp. Masses 33 | m c = 1:8 GeV (22) | m c = 1:8 GeV 26 | mc = 1:2 GeV [Our work] | Our QIE [MeV] N/E/VP | ||
| 1S | 3.067 | 3.104 | 3.097 | 3.066 | 666/ | 660/ | 662 |
| 2S | 3.649 | 3.703 | 3.673 | 3.764 | 1364/ | 1250/ | 1211 |
| 3S | 4.040 | 4.090 | 4.017 | 4.208 | 1808/ | 1640/ | 1624 |
| 4S | 4.415 | 4.375 | 4.276 | 4.545 | 2145/ | 2015/ | 1937 |
| 5S | - | 4.692 | 4.487 | 4.824 | 2424/ | --/ | 2194 |
| 1P | 3.525 | 3.572 | 3.524 | 3.566 | 1166/ | 1125/ | 1042 |
| 2P | - | 3.986 | 3.907 | 4.055 | 1655/ | --/ | 1480 |
| 3P | - | 4.280 | 4.186 | 4.418 | 2018/ | --/ | 1813 |
| 4P | - | 4.580 | 4.410 | 4.714 | 2314/ | --/ | 2086 |
| 5P | - | 5.034 [27] | - | 4.969 | 2569/ | --/ | 2320 |
| 1D | 3.769 | 3.806 | 3.791 | 3.902 | 1502/ | 1369/ | 1388 |
| 2D | 4.159 | 4.185 | 4.090 | 4.292 | 1892/ | 1759/ | 1713 |
| 3D | - | 4.474 | 4.328 | 4.605 | 2205/ | --/ | 1991 |
| 4D | - | 4.898 [49] | - | 4.871 | 2471/ | --/ | 2231 |
| 5D | - | - | -- | 5.107 | 2707 | --/ | 2444 |
Table II Masses [Gev] for b
| nL | Exp. Masses 33 | m b = 5:2 GeV 22 | m b = 5:2 GeV 26 | m b = 4:668 GeV [Our work] | Our QIE [MeV] N/E/VP | ||
| 1S | 9.444 | 9.473 | 9.460 | 9.444 | 110/ | 108/ | 122 |
| 2S | 10.023 | 10.024 | 10.034 | 10.098 | 764/ | 687/ | 651 |
| 3S | 10.355 | 10.327 | 10.356 | 10.482 | 1148/ | 1019/ | 1017 |
| 4S | 10.579 | 10.593 | 10.589 | 10.766 | 1432/ | 1243/ | 1283 |
| 5S | 10.865 | 10.788 | 10.776 | 10.998 | 1664/ | 1529/ | 1498 |
| 1P | 9.900 | 9.912 | 9.902 | 9.930 | 596/ | 564/ | 496 |
| 2P | 10.260 | 10.275 | 10.261 | 10.358 | 1024/ | 924/ | 890 |
| 3P | -- | 10.580 | 10.512 | 10.665 | 1331/ | --/ | 1178 |
| 4P | -- | 10.703 | 10.711 | 10.911 | 1577/ | --/ | 1408 |
| 5P | -- | 11.013 [48] | - | 11.119 | 1785/ | --/ | 1602 |
| 1D | 10.161 | 10.156 | 10.162 | 10.234 | 900/ | 825/ | 810 |
| 2D | -- | 10.434 | 10.433 | 10.565 | 1231/ | --/ | 1093 |
| 3D | -- | 10.625 | 10.643 | 10.825 | 1491/ | --/ | 1328 |
| 4D | -- | 10.934 [48] | - | 11.043 | 1709/ | --/ | 1529 |
| 5D | -- | 11.143 [48] | - | 11.232 | 1898/ | --/ | 1703 |
2.Numerov method
The non-relativistic kinetic energy operator for a two quark system is
where
If these two quarks are moving in a spherically symmetric potential that depends only
on their mutual separation
where
where we define
as an operator for QIE. In what follows, we obtain the charmonium and bottomonium spectra by solving the SWE with the SL potential 27
having a and b as free parameters. We fix these parameters to the lightest
whereas the bare quark masses are taken to be
In this form we parametrize charmonium mass spectrum as
In order to solve the corresponding SWE in Eq. (4) we discretize its radial coordinate 𝑟 into N equidistant points ri separated a distance d within a preselected characteristic length rmax suitable for the description of heavy meson spectra and represent the kinetic operator in Eq. (4) in terms of the two trigonal matrices
such that Eq. (4) is expressed in the form as in Refs. 24-26
where
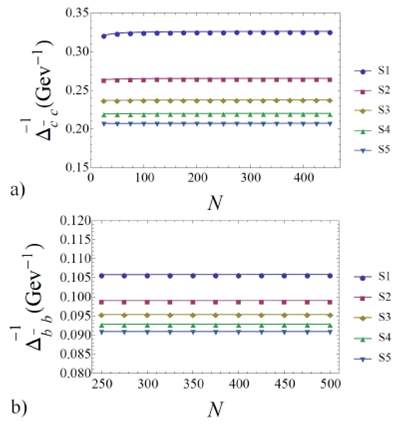
Figure 1 Stability test of the number of grid points for the prediction of the
(inverse) mass of S-states for c
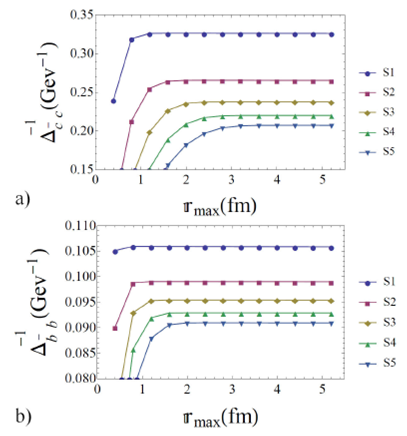
Figure 2 Stability test of the size of integration interval for the prediction
of the (inverse) mass of S-states for c
2.1.Spectra
Numerical solution of Eq. (10) gives wavefunctions corresponding to spin averaged
masses of charmonium and bottomonium. These are our well behaved spin averaged
orthonormal wavefunctions plotted for S, P and D states in Figs. 3 and4. The spin
averaged masses are shown in Tables I and
II and compared against the
experimental values 39 and
other theoretical findings. It is important to note that finding the correct
interaction energy between quarks (QIE) is a key feature for the success or
failure of a quark model and is a real essence of understanding the matter in
visible universe. The authors in Ref.23 and Ref.27 used charm quark mass 1.8 GeV which is 600 MeV
more than our bare charm quark mass. It means that these authors estimated
interaction energy 600 MeV smaller in charmonium system than ours. As for the
bottom quark is concerned, these authors estimate the interaction energy to be
1066 MeV smaller when compared to ours. The correct input mass to SWE produces
correct predictions and bare quark masses available so far are not less than
being the correct masses of charm in Eq. (B.1) and bottom in Eq. (B.2). So our
calculated interaction energies for charmonia and bottomonia must be correct in
our bare quark model (BQM). A quick analysis of QIE in Tables I and II shows
interaction energy in nL spin averaged states for bottomonia is smaller than
that for charmonia, and QIE for (n + 1)L state is larger than for nL. As a
complementary note, in the Appendix A we
have calculated these mass spectra by including spin-spin, spin-orbit, and
tensor interactions between quark Q and antiquark
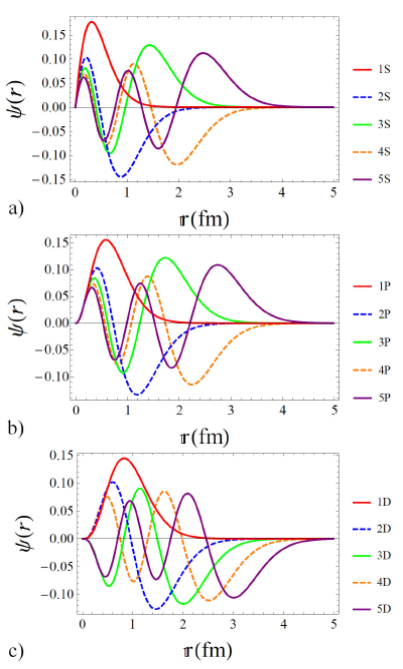
Figure 3 Wave functions for first five S-states (upper panel), P- states
(mid pannel) and D-states (lower panel) of c
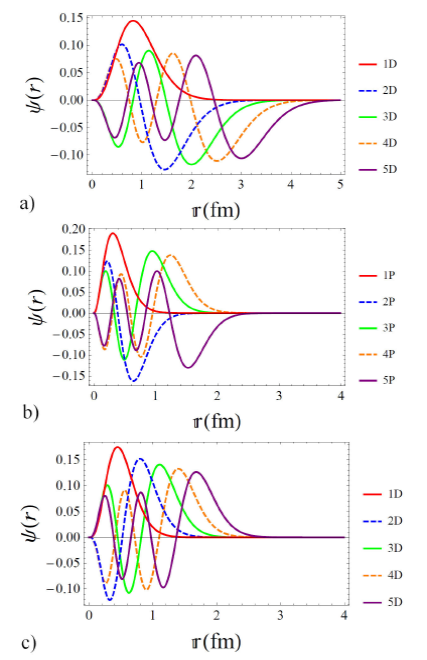
Figure 4 Wave functions for first five S-states (upper panel), P- states
(mid panel) and D-states (lower panel) of b
As for the size of the bound states, the root-mean-square radii
where the symbols n and
Radii from Eq. (11) and momentum width from Eq. (12) for different states are reported in Table III. A variation of momentum width with the size of the S, P and D states of charmonia and bottomonia are depicted on right panels in Figs. 5 and6, along with the analytical expressions for momentum width as functions of instantaneous quark separation r. From Table III we observe that bottomonia are more compact objects than corresponding charmonia. Furthermore the charmonia sizes are roughly twice as large as those of the similar states of the bottomonia while momentum width for c-quark mesons is approximately half that of the b quark.
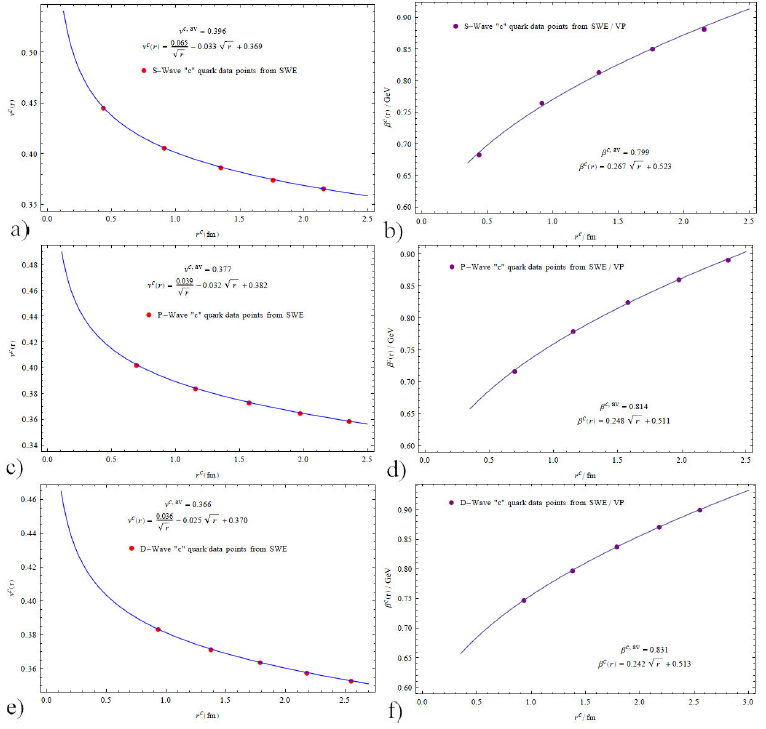
Figure 5 The velocities and momenta of charm quark within c
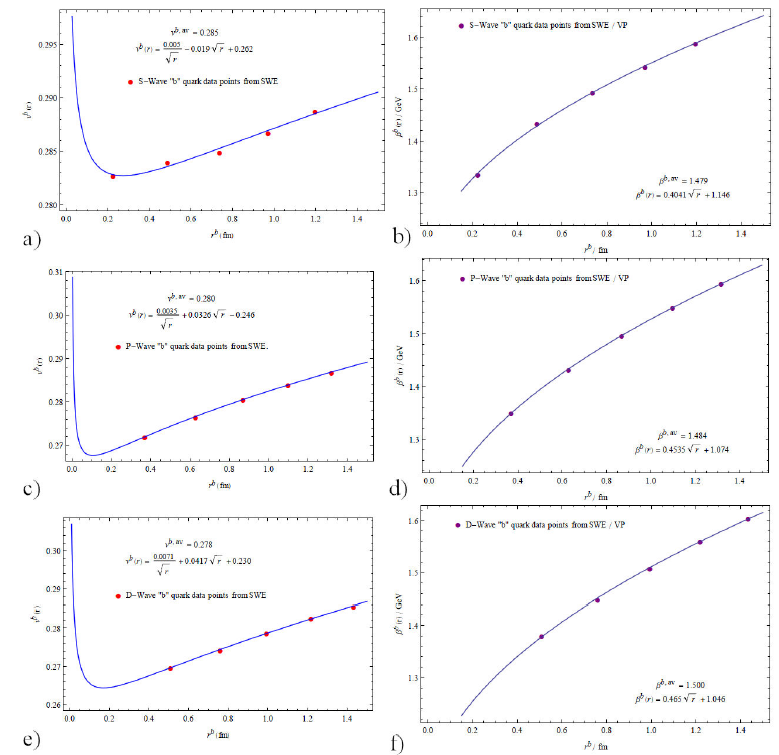
Figure 6 The velocities and momenta of bottom quark within b
Table III Radii
| nL |
|
|
|
|
||||||
| 2S | 0.915/ | 0.922/ | 0.91 | 0.765/ | 0.760 | 0.488/ | 0.501/ | 0.545 | 1.434/ | 1.397 |
| 3S | 1.352/ | 1.363/ | 1.38 | 0.813/ | 0.810 | 0.737/ | 0.755/ | 0.805 | 1.493/ | 1.457 |
| 4S | 1.762/ | 1.773/ | 1.87 | 0.851/ | 0.846 | 0.972/ | 0.991/ | 1.030 | 1.544/ | 1.514 |
| 5S | 2.151/ | 2.161/ | 2.39 | 0.882/ | 0.879 | 1.200/ | 1.216/ | 1.232 | 1.588/ | 1.562 |
| 1P | 0.697/ | 0.775/ | 0.71 | 0.717/ | 0.645 | 0.370/ | 0.416/ | 0.435 | 1.350/ | 1.202 |
| 2P | 1.155/ | 1.195/ | 1.19 | 0.779/ | 0.753 | 0.628/ | 0.658/ | 0.711 | 1.432/ | 1.368 |
| 3P | 1.577/ | 1.601/ | 1.67 | 0.824/ | 0.812 | 0.869/ | 0.893/ | 0.945 | 1.496/ | 1.456 |
| 4P | 1.976/ | 1.992/ | - | 0.860/ | 0.853 | 1.097/ | 1.118/ | 1.154 | 1.549/ | 1.521 |
| 5P | 2.343/ | 2.367/ | - | 0.891/ | 0.887 | 1.317/ | 1.336/ | 1.346 | 1.594/ | 1.572 |
| 1D | 0.936/ | 1.097/ | 0.96 | 0.748/ | 0.638 | 0.507/ | 0.601/ | 0.593 | 1.379/ | 1.165 |
| 2D | 1.380/ | 1.472/ | 1.44 | 0.797/ | 0.747 | 0.760/ | 0.818/ | - | 1.448/ | 1.345 |
| 3D | 1.791/ | 1.850/ | 1.94 | 0.838/ | 0.811 | 0.994/ | 1.036/ | - | 1.508/ | 1.448 |
| 4D | 2.178/ | 2.220/ | - | 0.871/ | 0.856 | 1.218/ | 1.251/ | - | 1.559/ | 1.560 |
| 5D | 2.497 | /2.581/ | - | 0.900/ | 0.891 | 1.434/ | 1.460/ | - | 1.604/ | 1.575 |
3.Other quarkonia observables
From the discussion of the previous section, we obtain a few parameters that allow us to characterize the dynamics of these heavy quark systems.
3.1.A model for quark velocities
Quark velocity is a vital ingredient in taking a decision whether to describe
quark dynamics in QCD perturbatively or non-perturbatively, and in the
determination of hadron masses using string quark model Ref.46. The root-mean-square
velocity of bottom quark in the
where β is the quark momentum found from Eq. (12), mQ is the bare quark mass. A second parametrization is based on our model that whatever is present in the meson in addition to quarks half of the meson mass should come from one quark and its dressing. In other words, the quark has to drag along it the field it is moving in. So we assume its inertia as half of the meson mass and thus we introduce
where Δ is the
Table IV Velocities from SWE and our VP (Sec. 4) in natural units, of the charm quark in orbitally and radially excited states of charmonium.
| States (n) | S | P | D | |||
| vF | vS,SW E/vS,V P | vF | vS,SW E/vS,V P | vF | vS,SW E/vS,V P | |
| 1 | 0.59 | 0.445/0.453 | 0.60 | 0.402/0.375 | 0.62 | 0.383/0.337 |
| 2 | 0.64 | 0.406/0.420 | 0.65 | 0.384/0.388 | 0.66 | 0.371/0.363 |
| 3 | 0.68 | 0.386/0.401 | 0.69 | 0.373/0.385 | 0.70 | 0.364/0.369 |
| 4 | 0.71 | 0.374/0.390 | 0.72 | 0.365/0.380 | 0.73 | 0.357/0.370 |
| 5 | 0.74 | 0.366/0.383 | 0.74 | 0.358/0.376 | 0.75 | 0.353/0.368 |
Table V Velocities from SWE and our VP (Sec. 4) in natural units, of the bottom quark in orbitally and radially excited states of bottomonium.
| States(n) | S | P | D | |||
| vF | vS,SW E/vS,V P | vF | vS,SW E/vS,V P | vF | vS,SW E/vS,V P | |
| 1 | 0.286 | 0.283/0.289 | 0.289 | 0.272/0.244 | 0.295 | 0.270/0.229 |
| 2 | 0.307 | 0.284/0.280 | 0.306 | 0.276/0.268 | 0.310 | 0.274/0.258 |
| 3 | 0.319 | 0.285/0.282 | 0.321 | 0.281/0.277 | 0.323 | 0.279/0.271 |
| 4 | 0.331 | 0.287/0.285 | 0.332 | 0.284/0.283 | 0.334 | 0.282/0.280 |
| 5 | 0.340 | 0.289/0.288 | 0.342 | 0.287/0.287 | 0.344 | 0.286/0.285 |
We plot quark velocities versus radii of mesons in their different quantum states
in Figs. 5 and6. We observe that for
while the momentum widths behave as
where
3.2.Annihilation decay rates
To further strengthen our use of bare quark masses in the non-relativistic
potential model and the claimed improved accuracy of the Matrix Numerov method,
we have opted to calculate the various decay rates of spin averaged S-wave
charmonia and bottomonia. Contrary to the general practice of proposing
Gaussian, or hydrogenic functions with one or two free parameters, we have
calculated the wave functions for the spin averaged quarkonia as solutions of
SWE. The leptonic
where
A comprehensive review about the strong running coupling constant αs within the effective potential approach is given in section 4.3 of the Ref.56. Our values of the strong coupling constant are in agreement with the findings of that work.
Annihilation decay rates are reported in Tables VII toXVIII along with a comparison against experimental results and other theoretical calculations where available.
Table VI The strong running coupling α s
| Quarkonia(nS) | Γ ggg | Γ γγγ | Γ γgg | Γ gg | Γ γγ | ||
| c |
0.0147 | 0.1834 | 0.1948 | 0.2244 | 0.2780 | 0.5435 | 0.2872±0.1328 |
| b |
0.4268 | 0.2091 | 0.2475 | 0.0943 | 0.2968 | 0.7771 | 0.4058±0.1946 |
Table VII Leptonic decay widths [keV] of spin averaged S-wave c
| State | Our Γ(nS)/Γc(nS) | Exp. [38] | [39] | [40] | (Γ (nS−> e + e - ) / Γ 1S->e + e - ) our/Exp. [26] |
| 1S | 5.55 | 5.55 | 5.63 | 3.112 | 1.00/1.00 |
| 2S | 2.18 | 2.33 | 2.19 | 2.197 | 0.39/(0.45±0.08) |
| 3S | 1.34/0.91 | 0.86 | 1.20 | 1.701 | 0.16/(0.16±0.04) |
| 4S | 0.97/0.63 | 0.58 | 0.63 | - | 0.11/(0.11±0.04) |
| 5S | 0.76/0.47 | - | 0.24 | - | 0.08/- |
Table VIII Three-gluon decay widths [keV] of spin averaged S-wave c
| State | Our Γ(nS)/Γc(nS) | Exp. [38] | [41] | [42] | (Γ (nS−> ggg)/Γ (1S− > ggg)) our/Exp. |
| 1S | 59.45 | 59.55 | 269.06 | 52.8±5 | 1.00/1.00 |
| 2S | 35.26/30.48 | 31.38 | 112.03 | 23±2.6 | 0.51/0.53 |
| 3S | 27.14/23.52 | - | 94.57 | - | 0.40/- |
| 4S | 22.85/19.85 | - | 88.44 | - | 0.33/- |
| 5S | 20.12/17.38 | - | 85.30 | - | 0.29/- |
Table IX Three-photon decay widths [eV] of spin averaged S-wave c
| State | Our Γ(nS)/Γc(nS) | Exp. [38] | [41] | (Γ (nS− > γγγ)/Γ (1S− > γγγ)) our/Exp. |
| 1S | 1.08 | 1.08±0.032 | 3.95 | 1.00/1.00 |
| 2S | 0.64/0.45 | - | 1.64 | 0.42/- |
| 3S | 0.49/0.33 | - | 1.39 | 0.31/- |
| 4S | 0.42/0.27 | - | 1.30 | 0.25/- |
| 5S | 0.37/0.23 | - | 1.25 | 0.21/- |
Table X Two-photon decay widths [keV] of spin averaged S-wave c
| State | Our Γ(nS)/Γ c (nS) | Exp. [38] | [40] | [41] | (Γ (nS− > γγ)/Γ (1S− > γγ)) our/Exp. |
| 1S | 5.10 | 5.1±0.4 | 6.96 | 6.62 | 1.00/1.00 |
| 2S | 3.02/2.12 | 2.15±0.6 | 10.45 | 2.88 | 0.42/0.42 |
| 3S | 2.33/1.58 | - | 1.03 | 2.44 | 0.31/- |
| 4S | 1.96/1.28 | - | - | 2.30 | 0.25/- |
| 5S | 1.73/1.09 | - | - | 2.21 | 0.21/- |
Table XI Two-gluon decay widths [MeV] of spin averaged S-wave c
| State | Our Γ(nS)/Γ c (nS) | Exp. [38] | [44] | [45] | (Γ (nS− > gg)/Γ (1S− > gg)) our/Exp. |
| 1S | 28.64 | 28.6±2.2 | 13.07 | 15.70 | 1.00/1.00 |
| 2S | 16.99/10.05 | 14±7 | 9.53 | 8.10 | 0.35/(0.49±0.28) |
| 3S | 13.08/7.51 | - | 4.41 | - | 0.26/- |
| 4S | 11.01/6.16 | - | - | - | 0.22/- |
| 5S | 9.71/5.22 | - | - | - | 0.18/- |
Table XII (One-photon,two-gluon) decay widths [keV] of spin averaged S-wave c
| State | Our Γ(nS)/Γ c (nS) | Exp. [38] | [41] | (Γ (nS− > γgg)/Γ (1S− > γgg)) our/Exp. |
| 1S | 8.18 | 8.18±0.25 | 9.00 | 1.00/1.00 |
| 2S | 4.85/2.87 | 2.93±0.16 | 3.75 | 0.35/0.36 |
| 3S | 3.73/2.14 | - | 3.16 | 0.26/- |
| 4S | 3.14/1.76 | - | 2.96 | 0.22/- |
| 5S | 2.77/1.49 | - | 2.85 | 0.18/- |
Table XIII Leptonic decay widths [keV] of spin averaged S-wave b
| State | Our Γ(nS) | Exp. [38] | [46] | [47] | (Γ nS− > e+e− /Γ 1S− > e+e− ) |
| 1S | 1.336 | 1.34±0.018 | 0.998 | 1.60 | 1.00/1.00 |
| 2S | 0.610 | 0.612±0.011 | 0.439 | 0.64 | 0.46/0.46 |
| 3S | 0.412 | 0.443±0.008 | 0.341 | 0.44 | 0.31/0.33 |
| 4S | 0.318 | 0.322±0.041* | 0.298 | 0.35 | 0.24/0.24 |
| 5S | 0.262 | 0.310±0.070 | 0.265 | 0.29 | 0.20/0.23 |
*This decay width is not correct in Table (XVII) of the Ref. 59
Table XIV Three-gluon decay widths [keV] of spin averaged S-wave b
| State | Our Γ(nS)/Γ c (nS) | Exp. [38] | [59] | [58] | (Γ (nS− > ggg)/Γ (1S− > ggg)) our/Exp. |
| 1S | 44.14 | 44.13±1.09 | 50.8 | 47.6 | 1.00/1.00 |
| 2S | 23.05/17.44 | 18.8±1.59 | 28.4 | 26.3 | 0.40/(0.43±0.04) |
| 3S | 16.78/12.36 | 7.25±0.85 | 21 | 19.8 | 0.28/0.16 |
| 4S | 13.67/9.82 | - | 16.7 | 15.1 | 0.22/- |
| 5S | 11.77/8.26 | - | 14.2 | 13.1 | 0.18/- |
Table XV Three-photon decay widths [keV] of spin averaged S-wave b
| State | Our Γ(nS)/Γ c (nS) | Exp. [38] | [59] | [58] | (Γ (nS− > γγγ)/Γ (1S− > γγγ)) our/Exp. |
| 1S | 1.95 x 10-5/1.54 x 10-5 | - | 1.94 x 10-5 | 1.7 x 10-5 | 1.00/1.00 |
| 2S | 1.02 x 10-5 /7.72 x 10-6 | - | 1.09 x 10-5 | 9.8 x 10-6 | 0.50/- |
| 3S | 7.43 x 10-6 /5.48 x 10-6 | - | 8.04 x 10-6 | 7.6 x 10-6 | 0.36/- |
| 4S | 6.05 x 10-6 /4.35 x 10-6 | - | 6.36 x 10-6 | 6.0 x 10-6 | 0.28/- |
| 5S | 5.21 x 10-6 /3.66 x 10-6 | - | 5.43 x 10-6 | 0.24/- |
Table XVI Two photon decay widths [keV] of spin averaged S-wave b
| State | Our Γ(nS)/Γc(nS) | Exp. [38] | [59] | [58] | (Γ (nS− > γγ)/Γ (1S− > γγ)) our/Exp. |
| 1S | 1.05/0.83 | - | 1.05 | 0.94 | 1.00/1.00 |
| 2S | 0.55/0.42 | - | 0.489 | 0.41 | 0.51/- |
| 3S | 0.40/0.29 | - | 0.323 | 0.29 | 0.35/- |
| 4S | 0.32/0.23 | - | 0.237 | 0.20 | 0.28/- |
| 5S | 0.28/0.20 | - | - | - | 0.24/- |
Table XVII Two gluon decay widths [keV] of spin averaged S-wave b
| State | Our Γ(nS)/Γc(nS) | Exp. [38] | [59] | [58] | (Γ (nS− > gg)/Γ (1S− > gg)) our/Exp. |
| 1S | 17.90/14.08 | - | 17.9 | 16.6 | 1.00/1.00 |
| 2S | 9.35/7.07 | - | 8.33 | 7.2 | 0.50/- |
| 3S | 6.80/5.01 | - | 5.51 | 4.9 | 0.36/- |
| 4S | 5.54/3.98 | - | 4.03 | 3.4 | 0.28/- |
| 5S | 4.77/3.35 | - | - | - | 0.24/- |
Table XVIII One photon-Two gluon decay widths [keV] of spin averaged S-wave b
| State | Our Γ(nS)/Γc(nS) | Exp. [38] | [59] | [58] | (Γ (nS− > γgg)/Γ (1S− > γgg)) our/Exp. |
| 1S | 1.19 | 1.19 ± 0.33 | 1.32 | 1.2 | 1.00/1.00 |
| 2S | 0.62 | 0.612 ± 0.011 | 0.739 | 0.68 | 0.52/0.51 |
| 3S | 0.45/0.23 | 0.20 ± 0.04 | 0.547 | 0.52 | 0.19/0.17 |
| 4S | 0.37/0.18 | - | 0.433 | 0.40 | 0.15/- |
| 5S | 0.32/0.15 | - | 0.370 | - | 0.13/- |
3.2.1.The Velocity and Momentum Width Corrections In Annihilation decay rates
Most NR quark model calculations usually fail to produce decay rates agreeable with experiment. The root of this failure lies in the absence of proper account of velocities and momentum widths of the two valence quarks going to annihilate each other in a meson. We have found the momentum correction factor
in charmonia annihilation decays except for the decays to three gluons, where this factor is,
The momentum width correction factor in all bottomonia annihilation decays is
The velocity correction factor for all charmonia annihilation decays is
and this velocity factor in the case of bottomonia annihilation decay rates happens to be
except for annihilation to
where vSc and vSb are, respectively, the velocities of c
and b quarks from our velocity model in Eq. (14). For the case of quarkonia
annihilations, the overall correction factor is
4.A Variational Approach
A subtle combination of the Heisenberg uncertainty Principle and the variation of mesonic Hamiltonian can be used to estimate the masses of charmonium and bottomonium as follows. The radial Eq. (4) can be written as,
This means radial Hamiltonian becomes (because radial component of momentum operator
is
We have modeled the quark momentum of this equation in a peculiar way which is described next.
We define symmetric point as the one for which all three cartesian components of any 3-vector are equal in magnitude. This means in cartesian space,
This definition turns Eq. (30) into the following effective Hamiltonian:
Here we invoke the Heisenberg uncertainty Principle,
as follows: A little cerebration reveals that the equality sign in Eq. (34) would
hold for ideal systems (for which experimental as well as theoretical uncertainties
are frozen at the minimum possible values of
where δ is real, positive number more than one and we define it as,
where
Thus, from Eq. (35),
The use of Eq. (31) and Eq. (32) gives,
and, in our notation, Eq. (33) becomes
Now we use this expression for computing meson radii and masses in the follwing way.
Equation (37) makes Eq. (39) altogether a function of one variable
This is the Hamiltonian of our meson system
Its solution gives
Let us apply this general procedure to a concrete example in which SLIP is the Song-Lin potential,
Upon inserting this potential into Eq. (40), we reach at the transcendental relation
where
Equation (45) used in Eq.(31) with our SL parametrization Eqs. (7) and (8) give the
radii of
Substitution of the root Eq. (45) in Eq. (52) produces the meson mass,
The ground state mass formula is
and the higher states have the mass formula,
The masses of
Table XIX Masses (in [GeV ]) of higher S wave heavy quarkonia from our VP compared with those from Screened Cornell potential (SP), Refs. 59. Here, N is for “from Numerov method”.
| Quarkonia | 6S | 7S | 8S | 9S | 10S |
| 5.066/4.817/(5.164,4.973) | 5.281/5.014/- | 5.478/5.192/- | 5.673/5.356/- | 5.890/5.508/- | |
| 11.196/11.017/10.998 | 11.370/11.178/11.155 | 11.527/11.323/11.294 | 11.671/11.454 /- | 11.804/11.576/- |
Table XX Masses (in [GeV ]) of D-wave heavy quarkonia from our VP compared with those from Bethe-Salpeter equation, Ref. 60.
| Quarkonia | 1D | 2D | 3D | 4S | 5S | 6D | 7D |
| 3.789 /3.820 | 4.113/4.151 | 4.391 /4.405 | 4.631/4.611 | 4.844/4.781 | 5.035/- | 5.20/- | |
| 10.146/10.15 | 10.429 /10.45 | 10.664/10.70 | 10.865 /10.90 | 11.039 /11.08 | 11.195/- | 11.336/- |
There are some more add ons from our VP. We use Eq. (45) in Eq. (31) and then result
in Eq. (37) to get
5.Conclusion
In this article, we have explored the mass spectra of charmonia and bottomonia in a non-relativistic framework invoking the Song-Lin potential as the effective interaction that binds heavy quarks in these meson systems with a single set of parameters. By numerically solving the resulting SWE through the Numerov strategy, we were able to calculate spin averaged masses of S, P, D, F and G states. For the sake of illustration, we have not included in the discussion the techniques and ideas of spin or tensor interactions. These findings are straightforwardly extended in the Appendix A.
We have calculated S-wave annihilation decay rates without and with momentum width
and velocity corrections by using wave functions at contact obtained from MNM. The
agreement of theory with experiments after applying the corrections indicate that
expressions for these decay rates should be revisited by properly incorporating the
quark velocities and momentum widths so that the factor
The quark kinetic energies found from Table III using
Table XXI Masses (in [GeV]) of F -waves heavy quarkonia from our VP compared with those from Screened Cornell potential (SP) Refs. 60.
| Quarkonia | 1F | 2F | 3F | 4F | 5F | 6F | 7F |
| 4.056/4.071 | 4.3182 /4.406 | 4.556 /- | 4.770/- | 4.964 /- | 5.141/- | 5.3052 /- | |
| 10.380 /10.366 | 10.603/10.609 | 10.802/10.812 | 10.979 /10.988 | 11.138 /- | 11.281 /- | 11.4135/- |
Table XXII Masses (in [GeV]) of G-wave heavy quarkonia from our VP compared with those from Screened Cornel potential (SP) Refs. 59 and D. Ebert 61.
| Quarkonia | 1G | 2G | 3G | 4G | 5G | 6G | 7G |
| 4.2783/4.345 | 4.5008 /- | 4.7095 /- | 4.9023/- | 5.0804 /- | 5.2457/- | 5.4000 /- | |
| 10.570/10.534 | 10.756/10.747 | 10.929/10.929 | 11.087 /- | 11.232 /- | 11.366/- | 11.490/- |
Table XXIII Masses [GeV] for c
| nL | Expc |
(Numerov)
c |
Our VP | Exp
b |
(Numerov)b |
Our VP |
| 1S | 3.067 | 3.066 | 3.062 | 9.444 | 9.444 | 9.458 |
| 2S | 3.649 | 3.764 | 3.611 | 10.023 | 10.098 | 9.987 |
| 3S | 4.040 | 4.208 | 4.024 | 10.355 | 10.482 | 10.353 |
| 4S | 4.415 | 4.545 | 4.337 | 10.597 | 10.766 | 10.619 |
| 5S | 4.487 [26] | 4.824 | 4.595 | 10.865 | 10.998 | 10.834 |
| 1P | 3.525 | 3.566 | 3.442 | 9.900 | 9.930 | 9.832 |
| 2P | 3.907 [26] | 4.055 | 3.879 | 10.260 | 10.358 | 10.226 |
| 3P | 4.186 [26] | 4.418 | 4.213 | 10.512 [57] | 10.665 | 10.514 |
| 4P | 4.409 [26] | 4.714 | 4.486 | 10.711 [57] | 10.911 | 10.744 |
| 5P | 4.807 | 4.969 | 4.720 | 10.014 | 11.119 | 10.938 |
| 1D | 3.769 | 3.902 | 3.788 | 10.161 | 10.234 | 10.146 |
| 2D | 4.159 | 4.292 | 4.113 | 10.432 [57] | 10.565 | 10.429 |
| 3D | 4.328 [26] | 4.605 | 4.391 | 10.643 [57] | 10.825 | 10.664 |
| 4D | 4.520 | 4.871 | 4.631 | 11.011 | 11.043 | 10.865 |
| 5D | 4.885 | 5.107 | 4.844 | 11.389 | 11.232 | 11.039 |











 nueva página del texto (beta)
nueva página del texto (beta)




