1. Introduction

CuInTe₂ is a well-known semiconductor of the I-III-VI2 family, which crystallizes in a chalcopyrite structure, space group I 2d (N^◦121), with unit cell parameters a = 6.194(2) Å and c = 12.416(4) Å [¹,²]. Recently, attention has been focused to explore their potential application in thermoelectric technology due to their moderate electrical transports and low thermal conductivity. A dimensionless figure of merit zT(= α ² σT/κ, where α, σ, T, and κ are Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity, respectively) of 1.18 at 850 K has been reported, which is better than any other un-doped diamond-like material [³]. To enhance the figure of merit, CuInTe₂ can be doped or alloyed; throughout these procedures, it is possible to tune the carrier concentration optimizing both electrical conductivity (σ) and power factor (α ² σ) and also to create extrinsic defects which could greatly alter the electron and phonon transport properties. It has been reported [⁴] that when CuInTe₂ is doped with Cd according with the general expression CuIn _1−x CdxTe₂ (with x = 0,0.02, 0.05, and 0.1) the zT values were improved by over 100% at room temperature and around 20% at 600 K for x = 0.02 and 0.1, respectively. It had been also reported [⁵] that (CuInTe₂) _1−X (ZnTe) _X solid solutions (simultaneous Zn²⁺ substitution for both Cu⁺ and In³⁺) have a lower thermal conductivity than CuInTe₂ and attained zT = 0.69 at 737 K, which is 1.65 times higher than the zT value of Zn-free CuInTe₂.

Following this reasoning, the (CuInTe₂) _1−X (ZnTe) _X solid solutions system has been investigated, and more particularly the sample CuFeInTe₃, which corresponds to the value of x = 0.5 (see Fig. 1). This quaternary compound is a semiconductor, belonging to the I-II-III-VI3 family, which has been studied for spintronic applications with interesting magnetic, thermal and thermoelectric properties. GrimaGallardo et al. suggest a super-paramagnetism behavior for CuFeInTe₃ [⁶,⁷] and Cabrera et al. [⁸] have demonstrated that CuFeInTe₃ is a promising n-type thermoelectric material applicable at high temperatures.

FIGURE 1 Compositional representation of the Cu-Fe-In-Te quaternary solid solutions system. 

For this compound, there are no reports on its powder diffraction pattern or its crystalline structure in the appropriate databases reviewed: Powder Diffraction File [⁹], Inorganic Crystal Structure Database (ICSD) [¹⁰], and Springer Materials [¹¹]. Hence, here we present the structural characterization of the quaternary compound CuFeInTe₃ using the Rietveld method to establish its crystal structure and report its powder X-ray diffraction data. The chemical structure was validated using the Bond Valence Sum (BVS) calculations [¹²,¹³].

2. Experimental

3. Results and discussion

The experimental (Yobs in red) powder XRD pattern of CuFeInTe₃ is shown in Fig. 2. An automatic search in the PDF-ICDD database [⁹], using the software available with the diffractometer, indicated that the powder pattern contained small amounts of Fe _1.125 Te (PDF N^◦01-080-0280). Bragg positions of the diffraction lines from this compound are also indicated in Fig. 2. The 20 first peak positions of the main phase, CuFeInTe₃, were successfully indexed using the Dicvol04 program [¹⁴], in a tetragonal unit cell with parameters slightly shorter than those of the ternary chalcopyrite parent CuInTe₂ [²].

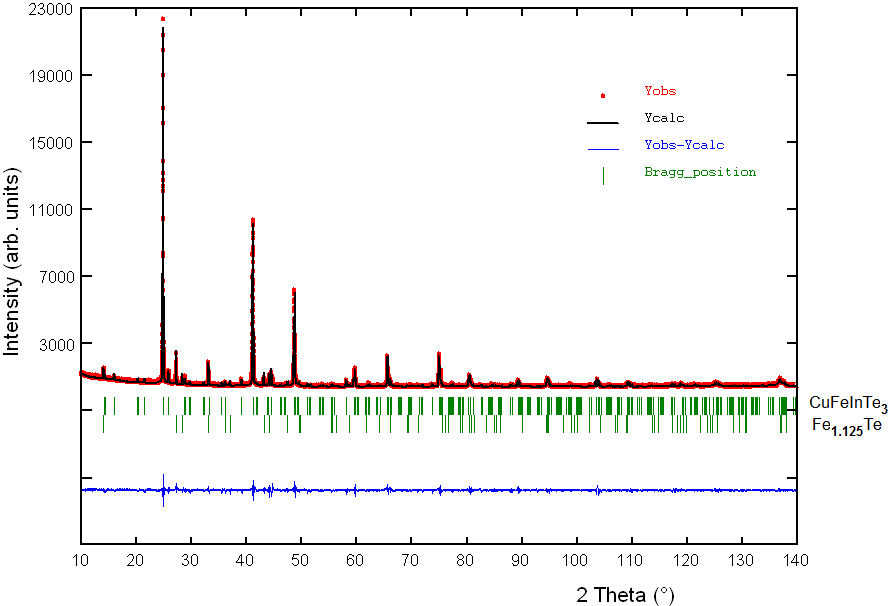
FIGURE 2 Rietveld refinement final plot of CuFeInTe₃. The lower trace is the difference curve between observed and calculated patterns. The Bragg reflections are indicated by vertical bars. 

A space group search using ExtSym program [¹⁵] suggested the space group P4¯2c which is consistent with the systematic absences.

The complete powder diffraction dataset was reviewed in the tetragonal space group P4¯2c by using the program NBS*AIDS [¹⁶]. From this analysis, the refined unit-cell parameters obtained were: a = 6.1891(3) Å and c = 12.3891(6) Å, with figures of merit M ₂₀ = 79.4 [¹⁷] and F ₃₀ = 43.3 (0.0045, 154) [¹⁸]. The resulting powder X-ray diffraction data for CuFeInTe3, together with the observed and calculated 2θ, the d-spacing’s as well as the relative intensities of the reflections, are given in Table I. These data will be submitted to the Powder Diffraction File of the International Centre for Diffraction Data [⁹].

The Rietveld refinement technique [¹⁹] with the software Fullprof version 7.30, March 2020 [²⁰] was used to determine the structure of CuFeInTe₃.

The starting structure model used was that of the parent compound CuFeInSe₃ [²¹] and the unit cell parameters were those obtained from the NBS*AIDS refinement. Atomic positions of the Fe _1.125 Te binary [²²] were included as a secondary phase in the refinement. The peak profiles were described using a parametrized pseudo-Voight function [²³,²⁴]. The background was described by the automatic interpolation of 123 points throughout the whole pattern. With the diffraction data available it was only possible to describe the thermal motion of the atoms by one overall isotropic temperature factor. A total of 23 parameters of the CuFeInTe₃ compound were refined, including peak shape parameters, scale factor, cell parameters, atomic coordinates, isotropic displacement parameters, and full-width at half-maximum (FWHM) parameters. The final Rietveld refinement led to agreement factors of: R _exp = 4.7%, R _p = 5.5%, R _wp = 6.1%, and S = 1.3, respectively Rexp=100[(N-P+C)/∑w(yobs2)]1/2, Rp=100∑|yobs-ycalc|/∑|yobs|, Rwp=100[∑w|yobs-ycalc|2/∑w|yobs|2]1/2, S=[RwpRexp], N − P +C is the number of degrees of freedom).

Figure 2 shows the results of the Rietveld refinement of CuFeInTe₃. The calculated powder pattern is shown as a solid black color line. The solid blue line is the difference between the calculated and experimental powder XRD patterns. The vertical green lines show expected Bragg diffraction peaks calculated as per space group P4¯2c. Details of refinement values are summarized in Table II. A semi-quantitative analysis [²⁵] from the final Rietveld refinement converged to the weight fraction percentages: CuFeInTe₃ (91.9%) and Fe _1.125 Te (8.1%). Table III shown the atomic coordinates, thermal displacement factors, bond distances, and angles for CuFeInTe₃. Unit cell diagram for this quaternary compound is shown in Fig. 3.

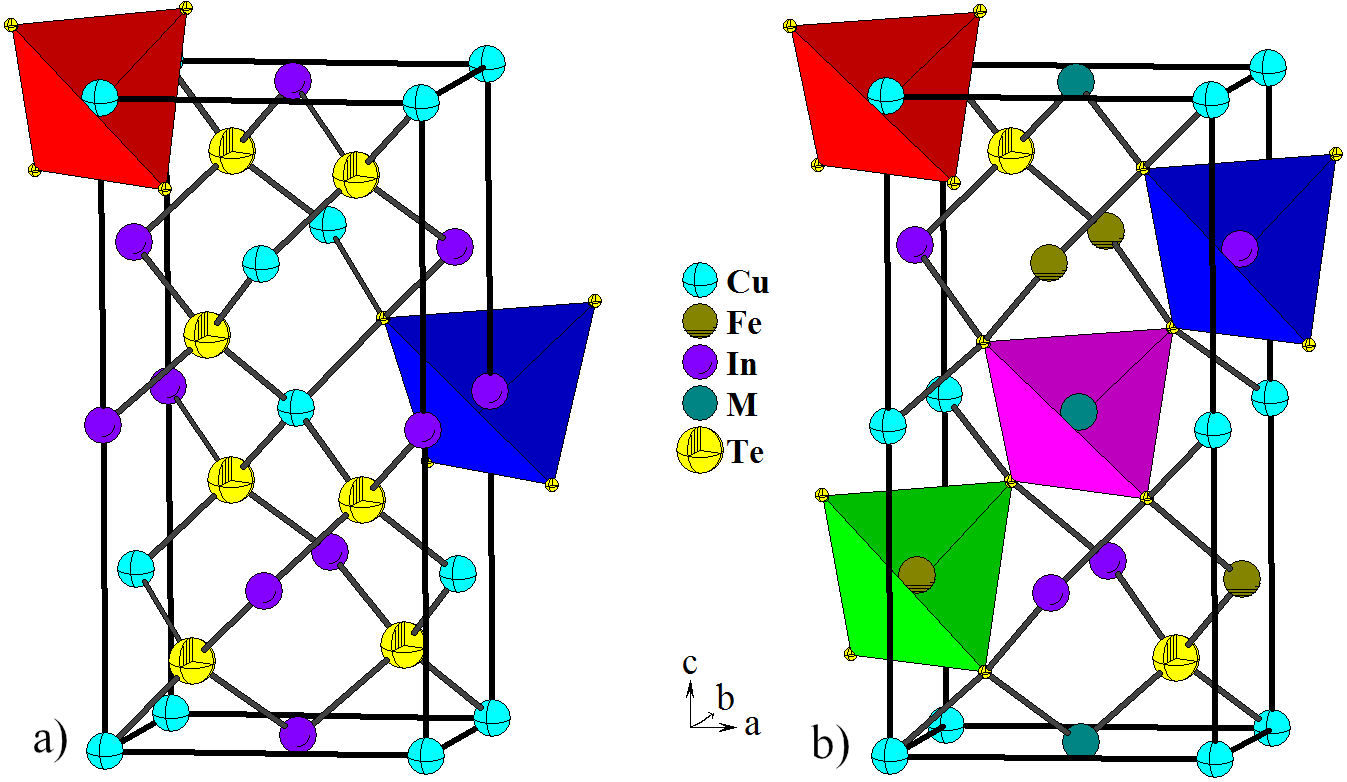
FIGURE 3 Unit cell diagram of the ternary CuInTe₂ (P4¯2c) chalcopyrite structure a) and the quaternary CuFeInTe₃ (P4¯2c) structure, b) showing the tetrahedra around the cations. The two structures differ in the arrangement of cations. 

In this system (CuInTe₂) _1−X (ZnTe) _X , with composition x = 0.5, introducing an additional cation (Fe) to the ternary CuInTe₂ leads to symmetry reduction from the chalcopyrite structure P4¯2c to a related P4¯2c known as P-chalcopyrite [²⁶]. In Fig. 3 it is possible to observe a comparison, with the tetrahedra pointed in the same direction, between the two structures: the ordered chalcopyrite P4¯2c structure of CuInTe₂ and the partially disordered P4¯2c structure of CuFeInTe₃. The quaternary compound CuFeInTe₃ has a normal adamantane-structure and can be described as a derivative of the sphalerite structure [²⁷]. The main features in the crystal structure are tetrahedral; each cation is coordinated by four anions (Te) and each anion is coordinated by four cations (one Cu, one Fe, one In, and one M) located at the corners of a slightly distorted tetrahedron. The tetrahedra containing the cations atoms have to mean Te...Te distances; 4.279(1) Å for M, 4.456(1) Å for Fe, 4.307(1) Å for Cu, 4.487(1) Å for In, respectively.

The interatomic Cu-Te [(2.665(1) Å], Fe-Te [2.726(1) Å], and In-Te [2.746(1) Å] are somewhat smaller than the sum of the respective ionic radii for structures tetrahedrally bonded [²⁸]. However, correlates well with those found in the adamantane structures CuInTe₂ [¹⁴], AgIn₅Te₈ [²⁹], CuTa₂InTe₄ [³⁰], Cu₃NbTe₄ [³¹], Fe₂GeTe₄ [³²], Ag₂FeGeTe₄ [³³], AgInTe₂ [³⁴], CuCo₂InTe₄ and CuNi₂InTe₄ [³⁵], Cu₃In₇Te₁₂ [³⁶] and Cu₃In₅Te₉ [³⁷].

The Bond Valence Sum (BVS) values, for Cu, Fe, In, and Te were calculated using the Brown-Altermatt empirical expression [¹¹,¹²]. The BVS of an atom i is defined as the sum of the bond valences V _ij of all the bonds from atoms i to atoms j and the usually accepted empirical expression for BVS is V _ij = exp[(R _o −d _ij )/B, where d _ij is the interatomic distance and B is taken to be a “universal” constant equal to 0.37 Å. The values for the reference distance Ro are 2.27 Å, 2.53 Å, and 2.69 Å, for Cu-Te, Fe-Te, and In-Te, respectively [¹²]. The calculated oxidation states agree with the expected formal oxidation states for Cu⁺, Fe²⁺, In³⁺, and Te²⁻ ions, whose results can also be seen in Table III.

4. Conclusions

The powder X-ray diffraction data and crystal structure of the super-paramagnetic semiconductor CuFeInTe₃ is reported. This compound, refined by the Rietveld method, crystallizes in a P-chalcopyrite structure with a partially disorder cation distribution. Structurally it corresponds to a new adamantane compound and consists of a three-dimensional arrangement of slightly distorted CuTe₄, FeTe₄, and InTe₄ tetrahedra connected by common corners. The chemical structural model was checked by analysis of the interatomic distances using the Bond Valence Sum (BVS) formula based on bondstrength examination.