1. Introduction
The wide-band gap semiconductor materials such as silicon carbide, gallium nitride, aluminum nitride, diamond, and others, are often referred to as third-generation semiconductor materials. Aluminum nitride (AlN) with a large direct band gap of 6.2 eV is a typical representative of these materials. Due to its ultra-wide direct band gap, high carrier mobility, large breakdown field, high thermal conductivity, high volume resistivity, high chemical and thermal stabilities, high dielectric strength, and low dielectric loss, make AlN an excellent material for novel electronic and opto-electronic device applications: i) laser diodes (LDs), deep-ultraviolet (DUV) solid-state light-emitting diodes (LEDs); ii) high frequency, high-power, and high-temperature electronic applications; iii) for packaging and substrates for high-density or high-power assemblies of microelectronic components [1,2,3].
The study of photoinjected (or photoexcited) carriers in AlN-based semiconductors can provide information regarding both their phonon and carrier dynamics properties, which are important for a better device design. Basic research regarding the ultrafast transport transient of hot carriers is relevant for technological applications in sub-micron devices.
In this paper, an analysis was performed to investigate the ultrafast transport properties of photoinjected carriers in wurtzite AlN subjected to electric fields up to 80 kV/cm. The optical and transport properties of semiconductors have been studied mainly by using Nonequilibrium Green’s Functions Techniques [24], Monte Carlo simulation [25,26], balance equation approach [27,28], Boltzmann transport equations [26,29,30], etc. In this paper was used the “Nonequilibrium Statistical Operator Method” (NESOM) [31-35]. The NESOM is a powerful formalism that seems to offer an elegant and concise way for an analytical treatment in the theory of irreversible processes, adequate to deal with a large class of experimental situations, and physically clear picture of irreversible processes. The NESOM is also practical and efficient in the study of the optical and carrier dynamics in semiconductors [36-42]. More specifically, a Non-Equilibrium Quantum Kinetic Theory [43] derived from NESOM was used in this paper.
2. The evolution equations
We consider a pure WZ AlN sample, with a concentration n of electron-hole pairs created by an intense laser light pulse. The photoinjected carriers were far from equilibrium with the lattice but thermalized between themselves by Coulomb interaction after a fraction of picosecond. A constant electric field Ɛ was applied to the sample to accelerate the carriers as well as relax the energy and momentum to the phonon field simultaneously. The sample was in contact with a thermal reservoir at temperature T 0.
The following variables were used to describe the nonequilibrium thermodynamic state
of the system: i) The reciprocal of the carrier nonequilibrium
temperature,
The nonlinear coupled set of integro-differential generalized transport equations that govern the time-evolution of these nonequilibrium thermodynamic variables is based on nonlinear quantum kinetic theory, which is based on a nonequilibrium statistical ensemble method [43], and the Markovian approximation is used [44]. The equations of evolution for the carriers’ linear momentum, carriers’ energy and LO, TO, AC phonons energy are as follows [43]:
In Eqs. (1) and (2) the first term on the right side is the force produced by the
electric field (
In Eq. (3) the first term on the right side accounts for the rate of energy pumped to the carrier system owing to the the electric field,
and the second term on the right side represents the rate of excess energy transferred to the phonons [43].
The populations of the LO- and AC- phonons [43] are expressed as follows:
where ω
(LO)
and ω
(AC)
are the frequencies of the (LO) or (AC) phonons,
respectively. We take the “Einstein model” dispersionless frequency relation for LO
phonons, that is:
In Eqs. (4) and (5) the first term on the right side are the gain of energy pumped on the phonons (LO and AC, respectively) by the “hot” carriers, and the second term on the right side in Eqs. (4) and (5) are the transfer, via anharmonic effects, of the energy of LO-phonons to the AC-phonons [43]
where τ op,an is the relaxation time obtained from the band width from Raman scattering experiments [49] and V cell is the volume of the unit cell.
The second term on the right side in Eq. (5) is the same of Eq. (4), but with the opposite sign. The last term in Eq. (5) is the contribution of thermal diffusion to the reservoir (thermal bath) at temperature T 0.
Finally, it noteworthy that, to close the system of equations, we must express the linear momentum of the carriers, and the energies of the phonons and carriers, as follows [43]:
3. Results
The calculations were performed in WZ AlN for photoinjected carriers with a concentration n = 1018 cm−3 and an excess energy of 0.6 eV per pair gained from photon absorption. After Coulomb thermalization, the initial carrier temperature was approximately T c (0) = 2321 K. The thermal bath temperature considered was T 0 = 300 K, and the carrier scattering mechanisms considered in the numerical calculations included piezoelectric, deformation acoustic and polar optical (or Fröhlich’s interaction). Table I summarizes the material parameters of the WZ AlN used in numerical calculations in this paper. In Table I, m 0 is the free electron mass.
TABLE I Parameters of wurtzite AlN.
| Parameter | Value |
| Electron effective mass, m*e | 0.48m0 [50] |
| Hole effective mass, m*h | 3.53m0 [40] |
| Band gap, Eg | 6.2 eV [51] |
| Intervalley energy separation | 0.7 eV [51] |
| Lattice parameter, a | 3.11 Å [52] |
| Lattice parameter, c | 4.98 Å [52] |
| Static dielectric constant, ε0 | 8.5 [53] |
| High frequency dielectric constant, ε∞ | 4.77 [53] |
| Optical phonon energy, |
99.2 meV [53] |
| Mass density, ρ | 3.23 g/cm3 [54] |
| Longitudinal sound velocity, v sl | 10127 m/s [55] |
| Transversal sound velocity, v st | 6333 m/s [55] |
| Acoustic deformation potential, E 1 | 9.5 eV [55] |
| Piezoelectric constant, h pz | 0.92 C/m2 [50] |
Figure 1 shows, for four values of the electric
field intensities, the time evolution of the nonequilibrium temperature of the
carriers, describing a extremely rapid process of relaxation of energy to the
lattice. It can be noticed that for
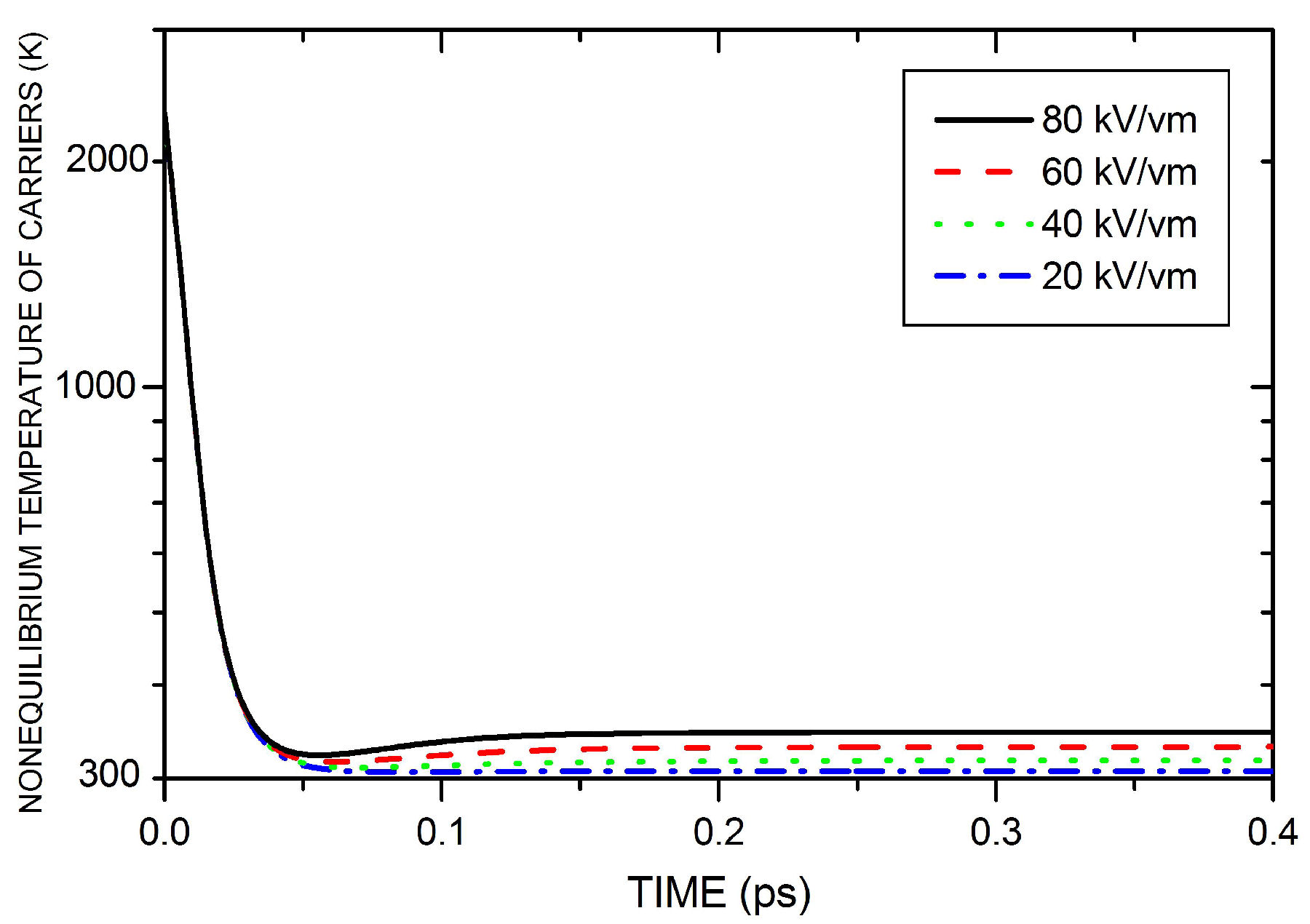
FIGURE 1 Time evolution of carriers nonequilibrium temperature in photoinjected WZ AlN for four electric field intensities.
Figure 2 shows, for an electric field strength
of 80 kV/cm, the evolution of the rate of change of the carriers nonequilibrium
temperature with respect to time,
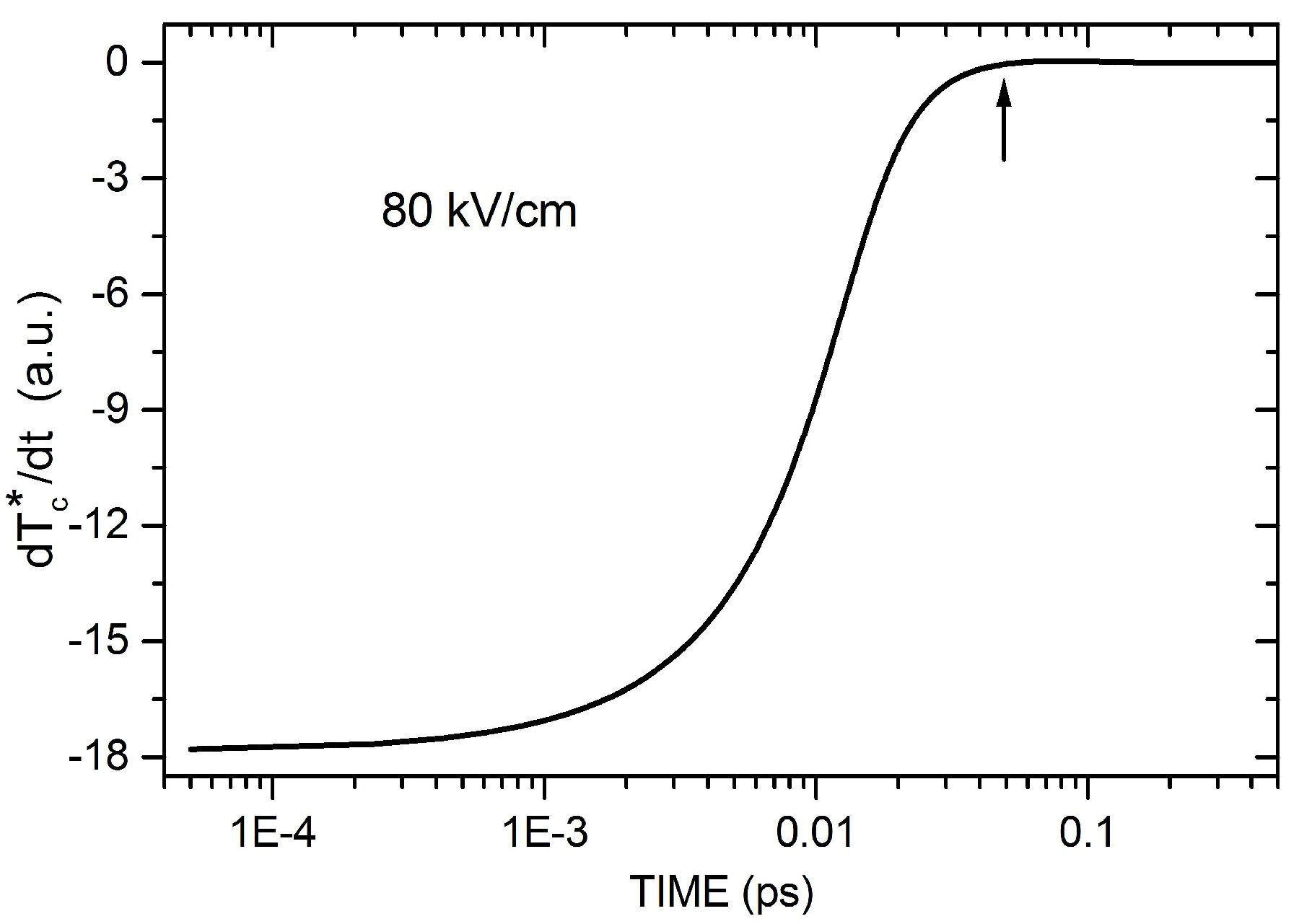
FIGURE 2 Time evolution of rate of change of carriers nonequilibrium temperature in photoinjected WZ AlN, in arbitrary units, for an electric field of 80 kV/cm.
Note that Eq. (3) comprises two terms:
Figure 3 shows the time evolution of the
electron (Fig. 3a) and hole (Fig. 3b) drift velocities for four electric field
intensities. After a transient regime in the order of picoseconds, a steady state
was achieved. Similar to Fig. 1, as larger the
electric field more time the system takes to reach the steady state. During the
transient regime, it can be noticed the behavior of the maxima existence for holes,
with one of the maxima corresponding to a velocity drift overshoot for fields larger
than approximately 40 kV/cm. The structured ultrafast hole drift velocity in
photoinjected WZ AlN is explained in this paper uniquely through the crossover of
the evolution curves for the transport and momentum relaxation times, whose
definition is based on the nonequilibrium variables used to describe the system
[56]. The values obtained for the hole
drift velocities are much smaller than those of electrons. This fact can be ascribed
to the holes having a higher effective mass than the electrons:
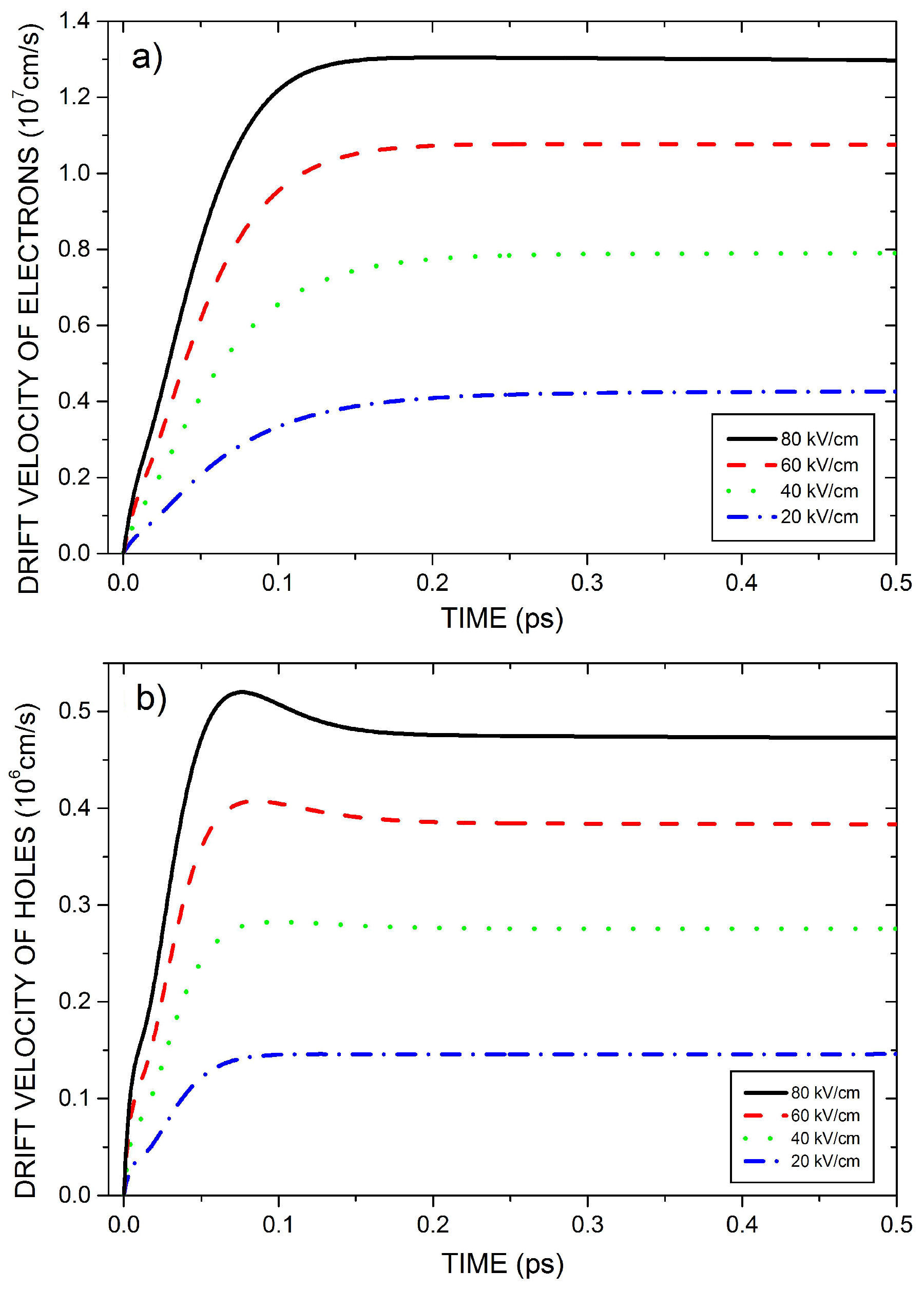
FIGURE 3 Time evolution of drift velocity: a) electrons and b) holes, in photoinjected WZ AlN for four electric field intensities.
Using the results of Fig. 3, we can derive the
mobility, M
e
(h), of the electrons and holes, as given by M
e
(h) = |v
e(h)
|/|Ɛ|. For a electric field of 20 kV/cm the electron and
hole mobility are approximately
Figure 4a) displays the time evolution of the nonequilibrium temperature of the LO-phonons for four different values of the electric field intensities. We can verify that the LO-phonon quasitemperature does not increase appreciably above equilibrium temperature T 0: approximately 3% for an electric field of 80 kV/cm, the higher field we have considered. Figure 4b) shows the time evolution of the nonequilibrium temperature of the AC-phonons for four different values of the electric field intensities. It is possible to verify that the temperature increase of the AC-phonons are irrelevant.
4. Conclusions
In this study, we obtain equations that govern the time evolution of the nonequilibrium state of highly photoinjected double plasma in the semiconductor WZ AlN subjected to electric field intensities to 80 kV/cm. For this study, we used a nonlinear quantum transport theory derived from the Nonequilibrium Statistical Operator Method [31-35]. We presented a study regarding ultrafast transport transient characteristics, focusing on the dependency of the nonequilibrium temperatures (carriers and phonons) as well as the electron and hole drift velocities on the electric field strength. Maxima of the hole drift velocity in its transient regime should be observable depending on the evolution of the nonequilibrium macroscopic state of the photoinjected carriers in WZ AlN. The transient regime occurred on a picosecond scale. The longitudinal optical phonons are slightly heated up in scattering events involving Frohlich interaction with the carriers,¨ and the temperature increase of the AC-phonons was irrelevant.











 nueva página del texto (beta)
nueva página del texto (beta)



