1.Introduction
The single fiber that hold two parallel cores is knowing as two-core optical fiber. Nowadays, a lot off attention have been focussed to the devices based on two-core fibers. Thus, some authors have been demonstrated that the double-core single-mode can be tailored as a directional coupler, polarization splitters and power depend nonlinear couplers 1. Furthermore, investigation of solitary waves in two-core optical fiber have been advanced beyond measure, such as soliton shape and mobility control in optical lattices 2, dark and bright solitons 3,4 and so on. Moreover, these localized solutions in optical fibers usually take the forms of shift solitons, spatiotemporal soliton, temporal soliton and spatial soliton 5. More recently, some works have been done to build soliton in a nonlinear coupler in a presence of a raman effect and solitary waves in asymmetric tin-core fibers 6,7. Today, analytical investigation of solitary waves become a big challenge, that is while some relevant methods have been used to construct exact solutions for partial differential equations (PDEs), such as unified method 8,9, initial condition field distributions 10, the simplest equation approach 11, the split-Step method 12, the first integral method 13, new extended direct algebraic scheme 14,15 and the generalized tanh method 16, just to name a few.
The following pair of nonlinear Schrödinger equations describes the pulse propagation through the two-core optical fibers 17. The model has been studied by Samir et al. 18, and novel traveling-waves solutions have been retrieved by help of Jacobian elliptic functions.
where
We aim in this paper to construct solitary waves and discussed the behavior of the
results obtained along with the constraint relation. To do so, we surmise
To obtain the travelign wave solutions of (2), the following ansatz is adopted:
where v is the velocity frame. Hence the phase
By inserting (3) into (2), we obtained the following set of equations
and
Multiplying (6) by
and thus, (4) gives
The formula given for (7) depends on
So, the following section adopted three relevant integration techniques, namely, the auxiliary equation method, the modified auxiliary equation method and the sine-Gordon expansion approach to derive bright and dark soliton solutions and we will discuss the behavior of the results obtained.
2.Glimpse of the methods
2.1.The auxiliary equation method
The following steps describe the auxiliary equation method 26,27. Considering a given nonlinear partial
differential equation (NPDE) with independent variables (x,t)
and dependent variables
Step 1: The traveling-wave solution of (10) is used in the following form
where v is the traveling-wave speed. Then (10) was converted into a nonlinear ordinary differential equation as follows
Step 2: Suppose that the exact solutions of (12) can be expressed
and
with
Step 3: Under the terms of the method, it is assumed that the solution of Eq.(12) can be written in the following form
where
Step 4: Substituting (16), (15) and (14) into (12) provides a
polynomial of
Step 5: To obtain the exact solutions to (10), the following solutions of (14) or (15) are used.
Case 1: for
Case 2: for
Case 3: for
Case 4: for
Case 5: for
where C 0, C 1, C 2, C 3 and C 4 are arbitrary constants. Therefore, using Eq.(17-21) and (16), the exact solutions to (10) can be obtained.
2.2.The modified auxiliary equation method
Investigation of exact traveling wave solutions of certain nonlinear partial differential equations by using the modified auxiliary equation method has been carried out recently 24-26.
Consider a nonlinear evolution partial differential equation as in Eq.(10) where
The main steps of the method to obtain exact solutions of (10) can be given as follows.
Step 1: Suppose that the formal solution of the ODE in (12) can be expressed as
where
where
Case 1: for
Case 2: for
Case 3: for
The explicit exact solutions of (10) can be obtained by inserting the values 0, A0, Ai, Bi (j = 1,2,3,…..n).
2.3.Sine-Gordon expansion approach
To integrate the ordinary differential equation (ODE) (12), we consider the sine-Gordon equation given by
The solutions of (27) are represented by
The series can be utilized to derive the solution of (12),
The parameter n can be obtained using the balancing principle. Making all the necessary computations, the solutions of the NPDE under consideration can be obtained.
3.Application of the methods
3.1.The Auxiliary equation method
Now, to use the homogeneous balanced principle between
Set 1:
Case 1: For
Case 2: For
Set 2:
Case 3: For
Eq.(34), one can find
Case 4: For C0 = C1 = 0, and
Case 5: For C0 = C1 = 0, and
3.2.The modified auxiliary equation method
Now, the MAE method will be utilized to get the general solution of Eq.(2). In this perspective, we obtain a system of algebraic equations which solves to
Set 1:
Set 2:
Using the values of the parameters in Set 1 given by (38), we get the solitary wave solutions of (2) in the following formulas:
When
or
When
or bright soliton solutions
When
Using the values of the parameters in Set 2 given by Eq.(39), we get the solitary
wave solutions of Eq.(2) in the following formulas: When
or
When
or bright soliton solutions
When
Figures 1 and 2 show (a) the spatiotemporal evolution in 3D, (b) contour plot, and
(c) the evolution at a different time in 2D of the bright and dark soliton
solutions in optical fibers for
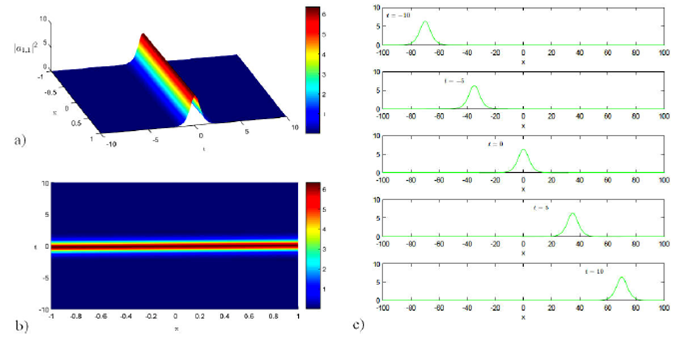
Figure 1 The plot of the bright soliton of |a 1;1 |2 of the solution Eq. (32) at A1 = 1, C2 = 0:019, C4 = -0:3, v = 7.
3.3.The Sine-Gordon expansion approach
Plugging the predicted solution (27) and its necessary derivatives into (9), we
get an over-determined system containing the combination of
Set 1:
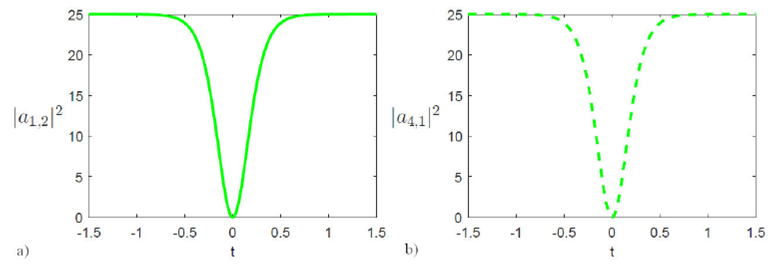
Figure 3 The plot of dark soliton |a 1;1 |2 of the solution Eq. (33) at A1 = 1:5, C0 = 0:5, C4 = 0:5, v = 4:5, a) [C2 = -0:25;C2 = -0:5;C2 = -0:75]; b) [C2 = -1:25;C2 = -1:50;C2 = -1:75] respectively.
Then, the solutions of (2) corresponding to (50) are
where (51) and (52) represent dark optical and singular soliton solutions, respectively.
Furthermore, (33) is read like (51) under the constraint conditions C2
= -1, and C4 = 1/2 (3). On the other side when
Set 2:
Then, the solutions of (2) corresponding to (53) are
where (54) and (55) represent bright optical and singular soliton solutions, respectively.
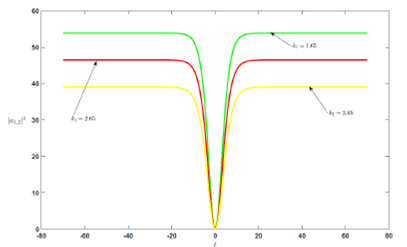
Figure 4 The plot of dark soliton |a 1;2 |2 of the solution Eq. (33) at [A1 = 1:5, C0 = 51:62, C2 = -2:31, C4 = 0:26, c = 1:2, v = 0:15, γ = 0:35, β2 = 1, k1 = 1:65], [A1 = 1:5, C0 = 38:43, C2 = -2:002, C4 = 0:026, c = 1:2, v = 0:15, γ = 0:35, β2 = 1, k2 = 2:65], [A1 = 1:5, C0 = 27:18, C2 = -1:68, C4 = 0:026, c = 1:2, v = 0:15, γ = 0:35, β2 = 1, k1 = 3:65] respectively.
Remark: By integrating from (4) with along to (7), we have
where
4.Conclusion
In this paper, we have investigated solitary waves for two-core optical fiber with coupling-coefficient dispersion and Kerr nonlinearity. It have been constructed an exact analytical soliton-like solutions by utilizing the traveling-wave hypothesis and hence the constraint relation fall out by adopting three integration techniques. By adopting the modified auxiliary equation and the sine-Gordon expansion approch, we obtain solitary waves; additionally, trigonometric function solutions and rational function solutions also emerge. Moreover, some new solitons solutions have been obtained, among which Eqs. (35)-(37), (40), (41), (43), (44), (49), and (55) are not reported in the standard integration method results summarized in of Ref. 30. The righteousness of the auxiliary equation method in this work is that, without a lot convoluted calculations, we obtain bright, dark and W-shape bright solitons. Thus, it is also important to note that the auxiliary equation method is independent of the integrability of the nonlinear differential equation (9). The obtained results will certainly have an important effect in nonlinear optical fibers in the field of solitary waves and can be helpful in describing communication systems ans ultra fast phenomena.
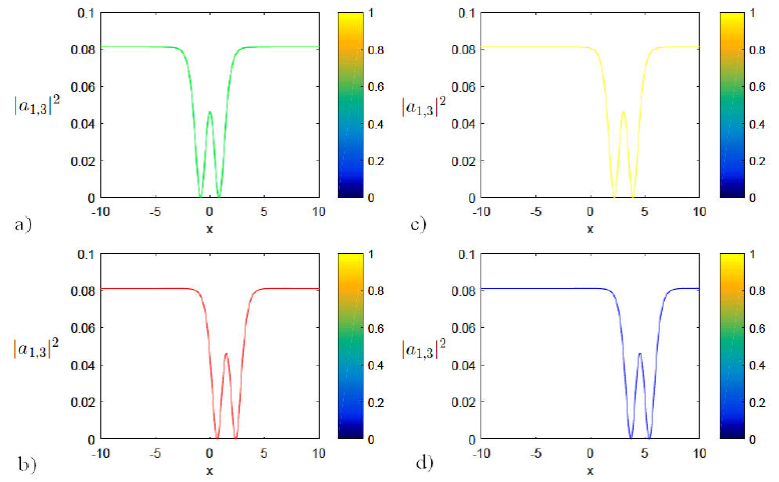
Figure 5 The plot of W-shape bright soliton |a 1;3 |2 of the solution Eq. (35) at a) [k1 = 0:975; c = 0:0461; v = 1:981; γ = 1:98005;A1 = 0:71; β2 = :90; t = 0], b) [k1 = 0:975; c = 0:0461; v = 1:981; γ = 1:98005;A1 = 0:71; β2 = :90; t = 3], c) [k1 = 0:975; c = 0:0461; v = 1:981; γ = 1:98005;A1 = 0:71; β2 = :90; t = 6], d) [k1 = 0:975; c = 0:0461; v = 1:981; γ = 1:98005;A1 = 0:71; β2 = :90; t = 9] respectively.











 nueva página del texto (beta)
nueva página del texto (beta)



