1.Introduction

The study of the fundamental or constituent blocks of matter has been for long time a fascinating field in physics. In the nineteenth century, the atom was considered to be the fundamental particle, the one from which all matter was composed. This idea was used to explain the basic structure of all elements ¹.

The problem of what were considered to be fundamental particles was resolved by the quarks. Because of the heavy masses of the constituent quarks, a good description of many features of these systems can be obtained using non-relativistic models where the quark-antiquark strong interaction is described by a phenomenological potential ². Heavy quarkonium systems have turned out to provide extremely useful probes for the deconfined state of matter because the force between a heavy quark and anti-quark is weakened due to the presence of gluons which lead to the dissociation of quarkonium bound states ³. The quarkonia with heavy quark and antiquark and their interaction are well described by the equation (SE) ⁴. The solution of the spectral problem for the SE with spherically symmetric potentials is of major concern in describing the spectra of quarkonia ⁵. Potential models offer a rather good description of the mass spectra of systems such as a bottomonium, and charmonium ⁶. In simulating the interaction potentials for these systems, confining-type potentials are generally used. The holding potential is the so-called Cornell potential with two terms, one of which is responsible for the Coulomb interaction of the quarks and the other corresponds to a confining term ⁷.

The solutions to the SE can be established only if we know the confining potential for a particular physical system. Till now, there are only a few confining potentials, like the harmonic oscillator and the hydrogen atom, for which solutions to the SE are found exactly ⁸.

The Hulthén potential takes the form ⁹

where α is the screening parameter and A₀ is the potential strength which is sometimes identified with the atomic number when the potential is used for atomic phenomena (10). It is a short-range potential which is applied in many branches of physics, such as nuclear and particle physics, atomic physics, solid state physics, and chemical physics ^11,12.

The Hellmann potential which is a superposition of an attraction Coulomb potential and a Yukawa potential can be expressed as ¹³.

where the parameters A₁ and A₂ denote the strength of Coulomb and Yukawa potentials respectively, α denotes the screening parameter, and r is the distance between two particles. These potentials have been used to study bound state problems by many researchers ^14-20. Recently, Inyang et al. ²¹ obtained the Klein-Gordon equation solutions for the Yukawa potential using the Nikiforov-Uvarov (NU) method. The energy eigenvalues were obtained both in a relativistic and non-relativistic regime. They applied the results to calculate heavy-meson masses of charmonium cc¯ and bottomonium bc¯. Apart from that, many researchers have provided approximate solutions to SE using different methods with Cornell potential. For instance, Vega and Flores ²² obtained the approximate solutions of the Schrödinger equation with the Cornell potential using variational method and super symmetric quantum mechanics (SUSYQM). Abu-Shady et al. ²³ studied the N-dimensional radial equation using the analytical exact iteration method (AEIM), in which the Cornell potential is generalized to finite temperature and chemical potential. In addition, Ciftci and Kisoglu ²⁴, solved non-relativistic arbitrary l-states of quarkonium through asymptotic iteration method (AIM). An analytic solution of the N-dimensional radial equation with the mixture of vector and scalar potentials via the Laplace transformation method (LTM) were studied in . Al-Jamel and Widyan ²⁶ studied heavy quarkonium mass spectra in a Coulomb field plus quadratic potential using NU method. Ibekwe et al. ²⁷ solved the radial SE with an exponential, generalized, harmonic Cornell potential using the series expansion method. Their results were used to calculate the mass spectra of heavy-mesons. Al-Oun et al. ²⁸ examine heavy quarkonia characteristics properties in the general framework of non-relativistic potential model consisting of a Coulomb plus quadratic potential. Chouikh et al. ²⁹ proposed an approach to achieve quantum computation with atomics qubits in a cavity QED. Recently, researchers have shown great interest in the combination of two or more potentials in both the relativistic and non relativistic approach. The fundamental nature of combining two or more physical potential models is to have a wider range of application ³⁰. For example, the Cornell potential which is the combination of the Coulomb potential with linear terms is used in studying the mass spectra for coupled states and for the electromagnetic characteristics of meson ³¹. For instance, William et al. ³² obtained bound state solutions of the radial equation by the combination of Hulthén and Hellmann potential within the framework of Nikiforov-Uvarov method. Also, Edet et al. ³³ obtained an approximate solution of the SE for the modified Kratzer potential plus screened Coulomb potential model using the Nikiforov-Uvarov method. In this present work, we aim to study the SE with the combination of Hulthén and Hellmann potential analytically by using the NU method and apply the results to calculate the mass spectra of heavy quarkonium particles such as bottomonium and charmonium, in which the quarks are considered as spinless particles for easiness, which have not been considered before using this potentials to the best of our knowledge. The adopted potential is of the form ³²

where A₀, A₁, and A₂ are potential strength parameters and α is the screening parameter. In other to make (3) temperature dependent, the screening parameter is replaced with the Debye mass m _D(T), which is temperature-dependent and vanishes at T→0 and we have,

We carry out a series expansion of the exponential terms in (4) up to order three in order to model the potential to interact in the quark-antiquark system and this yields,

We substitute (5) and (6) into (4) and obtain

where

The first term in (7) is the Coulomb potential that describes the short distance between quarks, while the second term is a linear term featuring confinement.

2.Approximate solutions of the equation with Hulthén plus Hellmann potential

The Schrödinger equation (SE) for two particles interacting via potential V(r) in three dimensional space, is given by ³⁴

where l, μ, r, and ℏ are the angular momentum quantum number, the reduced mass for the quarkonium particle, inter-particle distance and reduced plank constant respectively. We substitute (7) into (9) and obtain

Let,

Substituting (11) into (10), we have

Transforming the coordinate of (12) we set

Differentiating (13) and simplifying we have

Substituting (13) and (14) into (12) we have

Next, we propose the following approximation scheme on the term α1/x and α2/x2.

Let us assume that there is a characteristic radius r₀ of the meson. Then the scheme is based on the expansion of α1/x and α2/x2 in a power series around r₀, i.e. around δ≡1/r0, in the x-space up to the second order. This is similar to the Pekeris approximation, which helps to deform the centrifugal term such that the modified potential can be solved by the NU method ³⁵.

Setting y=x-δ and around y=0, it can be expanded into a series of powers as;

which yields

Similarly,

By substituting (18) and (17) into (15) , we obtain

where

Comparing Eq. (19) and Eq.(A1) we obtain

We substitute (21) into (A9) and obtain

To determine k, we take the discriminant of the function under the square root, which yields

We substitute (23) into (22) and have

For a physically acceptable solution, we take the negative part of (24) which is required for bound state problems and differentiate; this yields

Substituting (21) and (25) into (A7) we have

Differentiating (26) we have

By using (A10), we obtain

and using (A11), we obtain

Equating Eqs. (28) and (29), the energy eigenvalues of (10) are given

Enl=A012-mD(T)4δ+A2mD(T)3mD(T)2δ-mD2(T)-1,

3.Results

We calculate the mass spectra of the heavy quarkonium system such as charmonium and bottomonium that have the quark and antiquark flavor, and apply the following relation ^36,37

where m is quarkonium bare mass and Enl is energy eigenvalues. By substituting (30) into (44) we obtain the mass spectra for Hulthén plus Hellmann potential as

3.1.Discussion of results

We calculate the mass spectra of charmonium and bottomonium for states from 1S to 1F, by using Eq. (45). The free parameters of Eq. (45) are fitted with experimental data by solving two algebraic equations. Experimental data are obtained from ^38,39. For bottomonium bb¯ and charmonium cc¯ systems we adopt the numerical values of these masses as m_b = 4.823 and m_c = 1.209 respectively ⁴⁰. Then, the corresponding reduced mass are μb=2.4115 and μc=0.6045. The Debye mass m_D(T) is taken as 1.52 GeV by fitting with experimental data. We note that calculation of mass spectra of charmonium and bottomonium are in a good agreement with experimental data as well as the work of other researches as presented in Tables I and II. It is important to note that the values obtained are improved in comparison with works like that of Ref. ³⁵, as shown in Tables I and II in which the author investigated the N- radial SE analytically when the Cornell potential was extended to finite temperature.

Table I Mass spectra of charmoniumin (GeV) for Hulthén plus Hellmann potential, (m _c = 1:209 GeV, μ = 0:6045 GeV, A⁰ = -1:693 GeV, A₁ = 20:654 GeV, A₂ = 0:018 GeV, δ = 0:2 GeV, m _D (T) = 1:52 GeV, ℏ = 1). 

State	Present work	[35]	[24]	Experiment [38,39]
1S	3.096	3.096	3.096	3.096
2S	3.686	3.686	3.672	3.686
1P	3.521	3.255	3.521	3.525
2P	3.772	3.779	3.951	3.773
3S	4.040	4.040	4.085	4.040
4S	4.262	4.269	4.433	4.263
1D	3.768	3.504	3.800	3.770
2D	4.146	-	-	4.159
1F	3.962	-	-	-

Table II Mass spectra of bottomonium in (GeV) for Hulthén plus Hellmann potential, (mb = 4:823 GeV, μ = 2:4115 GeV, A₀ = -1:591 GeV, A₁ = 9:649 GeV, A₂ = 0:028 GeV, δ = 0:25 GeV, m _D (T) = 1:52 GeV, ℏ = 1). 

State	Present work	[35]	[24]	Experiment [38,39]
1S	9.460	9.460	9.462	9.460
2S	10.023	10.023	10.027	10.023
1P	9.861	9.619	9.9630	9.899
2P	10.238	10.114	10.299	10.260
3S	10.355	10.355	10.361	10.355
4S	10.579	10.567	10.624	10.580
1D	10.143	9.864	10.209	10.164
2D	10.306	-	-	-
1F	10.209	-	-	-

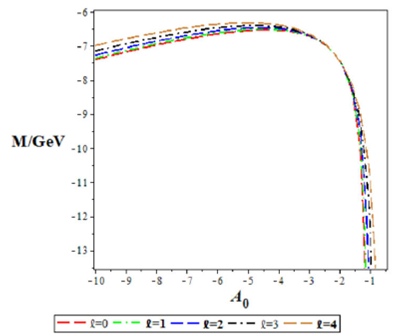
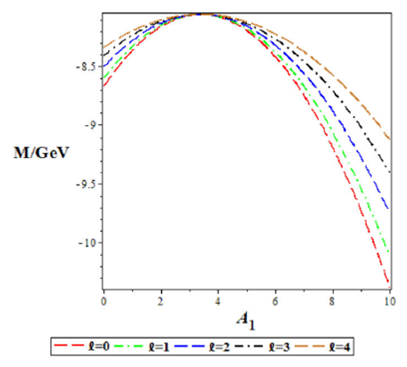
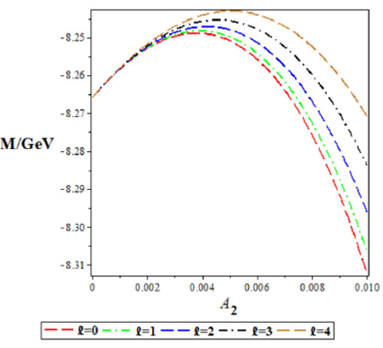
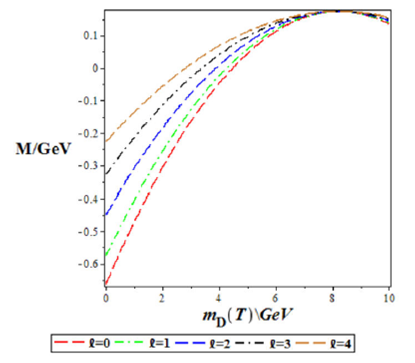
We also plotted the mass spectra energy as a function of potential parameters and Debye mass. In Figs. 1 and 2, the mass spectra energies increases to a peak and later decreases as potential parameters and increases, respectively. In Fig. 3 the mass spectra converges at the beginning, but spreads out and decrease monotonically with the increase in potential parameter A₂. Figure 4 show the increase in mass spectra as the Debye mass increases, for various angular quantum numbers.

Figure 1 Mass spectra variation with potential parameter A₀ for different quantum numbers. 

Figure 2 Mass spectra variation with potential parameter A₁ for different quantum numbers 

Figure 3 Mass spectra variation with potential parameter A₂ for different quantum numbers. 

Figure 4 Mass spectra variation with the Debye mass m _D (T) for different quantum numbers. 

4.Conclusion

In this study, we adopted Hulthén plus Hellmann potential models for quark-antiquark interaction. The potential was made to be temperature dependent by replacing the screening parameter with Debye mass which vanishes at. The Schrödinger equation is analytically solved using the Nikiforov-Uvarov method. We obtained approximate solutions of the eigenvalues and eigenfunction in terms of Laguerre polynomials. We applied the present results to calculate heavy-meson masses such as charmonium cc¯, and bottomonium bb¯ for states 1S to 1F which are in good agreement with experimental data and the work of others. Four special cases were considered when some of the potential parameters were set to zero, resulting into Hellmann potential, Yukawa potential, Coulomb potential, and Hulthén potential, respectively. Different plots of mass spectra versus different potential parameters and Debye mass were analyzed and discussed.