1. Introduction
Over the last few years, nonlinear Schrödinger’s equations (NLSEs) have attracted much attention in the field of research due to their numerous fascinating behaviour and countless characteristics. A large variety of these equations are utilized to describe important phenomena in different scientific fields like, plasma physics [1,2], condensed matter physics [3], convective fluids [5], optical fibers [6,7], solid state physics [8,9], hydrodynamic [10], water waves [11] and many other branches of engineering [12-14]. In past years, to find the exact solutions of NLSEs many powerful technique have been developed such as, the inverse scattering transformation [15], the homotopy perturbation method [16,17], the Darboux transformation method [18,19], the Sine-Gordon expansion method [20], Bernoulli sub-equation method [21], the modified auxiliary equation mapping method [22,23], the Riccati equation mapping method [4], the extended sinh-Gordon equation expansion method [24],the modify extended direct algebraic method [25].
The Heisenberg models of ferromagnetic spin chains with various magnetic reactions in the classical and semiclassical limits have been related with nonlinear evaluation equations (NLEEs). The nonlinear spin chain have wide range of applications in magnetic materials such as, sensors [26], microwave, date storage devices, communication system [27], signal processing devices and quantum computing. In this article, we have successfully investigated a variety of exact travelling wave solutions by employing extended rational trigonometric methods to construct the hyperbolic, trigonometric and complex function solutions moreover classify as dark, singular and periodic wave solutions. To study (2+1)dimensional Heisenberg ferromagnetic spin chains (HFSC) model of the the form [28,29].
here, Ψ is coherent amplitude. Hashemi transform it into fractional form:
where Ψ = Ψ(x,y,t) is the complex valued function of Heisenberg ferromagnetic spin chain, x and y are representing scaled spatial and t is the time coordinates respectively.
In recent times, a large number of scientists and researchers have been attracted to
HFSC models due to their significant and fascinating characteristics for
construction of different types of exact solutions in NPDEs.
The remaining paper is arranged as fellows: In Sec. 2 some sliton solutions to the HFSC model have been presented. The physical significance and graphical representation is presented in Sec. 3. In Sec. 4 finally the concluding remarks and behaviour of solution have been discussed.
2. Mathematical analysis
In this section, to obtain the exact solutions of Eq. (2) by applying following conformable fractional derivative [36]
By this definition and following complex travelling wave transformation
where
Putting Eq. (5) into Eq. (2), we obtain
where α 1, α 2, β 1 and β 2 real constants and are center of phase. where Θ represents the phase component, ρ is the velocity and ω is the frequency respectively.
2.1. Applications of the extended rational sine-cosine method
Assume that Eq. (6) has the solution of the form:
or of the form
where A 0, A 1 and A 2 are parameters that will be determined and ν represents wave number.
Family I
Now, substituting Eq. (7) into Eq. (6) and then setting each coefficients of all terms of cos m (νs) or sin m (νs) to zero, yields a system of algebraic equations. Then we obtain system of algebraic equations involving parameters A 0, A 1, A 2, µ, ν, λ, δ, ρ.
Solving this system, we yields the following set:
Case I:
Substituting these results into Eq. (5) by using Eq. (7) , we have
Case II:
Again, substituting these results into Eq. (5) by using Eq. (7), we obtain
provided that
Family II
Again, substituting Eq. (8) into Eq. (6) and then setting each coefficients of all terms of sin m (νs) or cos m (νs) to zero, yields a system of algebraic equations. Then we obtain system of algebraic equations involving parameters A 0, A 1, A 2, µ, ν, λ, δ, ρ.
This system, gives the following set of solutions:
Case I:
Substituting these results into Eq. (5) by using Eq. (8), we have
Case II:
Again, substituting these results into Eq. (5) by using Eq. (8), we obtain
provided that
2.2 Applications to the extended rational sinh-cosh method
Assume that Eq. (6) has the solution of the form:
or of the form
where A 0, A 1 and A 2 are parameters that will be determined and ν represents wave number.
Family I
Now, substituting Eq. (21) into Eq. (6) and then setting each coefficients of all terms of cosh m (νs) or sinh m (νs) to zero, yields a system of algebraic equations. Then we obtain system of algebraic equations involving parameters A 0, A 1, A 2, µ, ν, λ, δ, ρ. This system of equations are solved as follows:
Solving this system, we yields the following set of solutions with help of Mathematica:
Case I:
Substituting these results into Eq. (5) by using Eq. (21), we have
Case II:
Again, substituting these results for only the positive values into Eq. (21), we obtain
holds for
Family II
Again, substituting Eq. (22) into Eq. (6) and then setting each coefficients of all terms of sinh m (νs) or cosh m (νs) to zero, yields a system of algebraic equations. Then we obtain system of algebraic equations involving parameters A 0, A 1, A 2, µ, ν, λ, δ, ρ.
This system, gives the following set of solutions:
Case I:
Substituting these results into Eq. (5) by using Eq. (22), we obtain
Case-II:
Again, substituting these results into Eq. (5) by using Eq. (22), we obtain
provided that
3. Physical significance and graphical representations
In this section, we construct the physical interpretation to the some problem of the paper that add extra flavour to our analytical solutions of (2). For this purpose, graphical representations of some established problem are discussed and suitable choice of help us to construct dark, singular and traveling wave solutions. The graphically representations of some obtained solutions in two and three-dimensional are given from Figs. 1 to 7. Figure 1 for Eq. (13) and Fig. (2) for Eq. (19) represent periodic wave solutions and two-dimensional graphics limit cycle with suitable choice of parameters. Figure 5 for Eq. (27) and Fig. 7 for Eq. (33) show dark and singular wave solutions. Dark and singular wave solutions types presents in Figs. 3, 4 for Eq. (23) and Fig. 6 for Eq. (29).
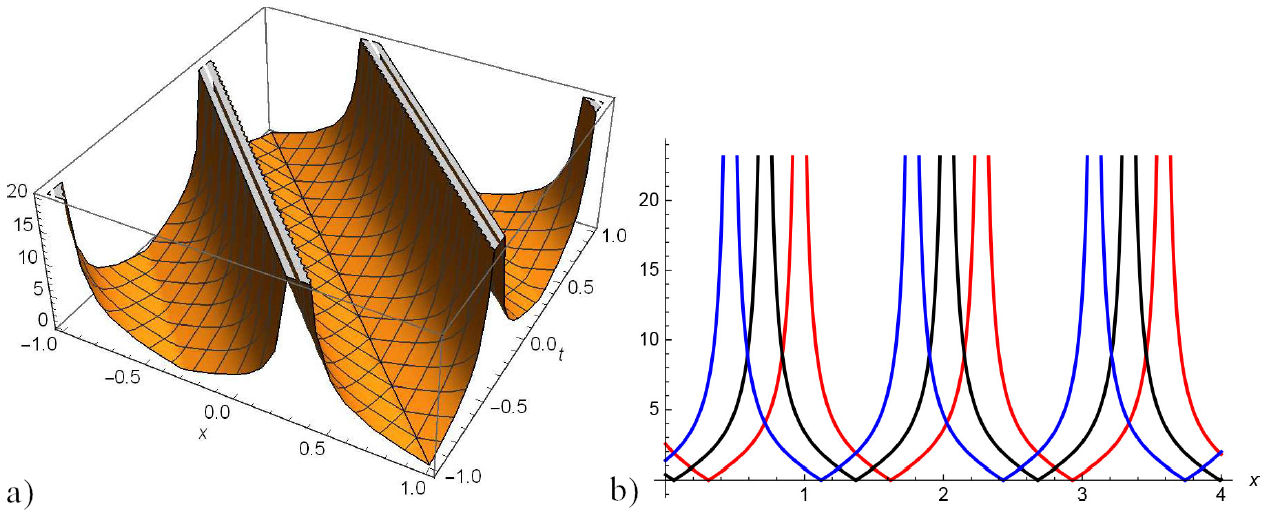
FIGURE 1 a) 3D and b) 2D surfaces for the |Φ 1,5 (x,y,t)| with −1 ≤ x,t ≤ 1 for the values µ = 1, η = 2.50, λ = 2.50, δ = 1.50, α = 1, α 1 = −1, α 2 = 1, β 1 = 2, β 2 = 1, θ = 0, ρ = 0, ω = 1, y = 0 and their projections at t = 1,1.25, 1.50.
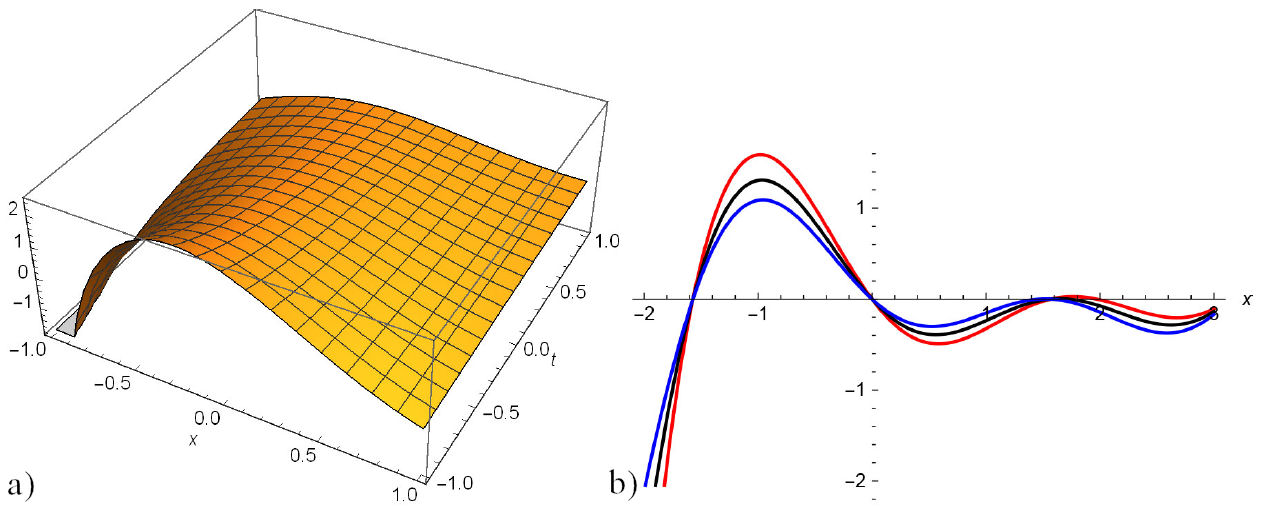
FIGURE 2 a) 3D and b) 2D surfaces of |Φ 2,5 (x,y,t)| with −1 ≤ x,t ≤ 1 for the values µ = 1, η = 2.50, λ = 2.50, δ = 1.50, α = 1, α 1 = 1, α 2 = 1, β 1 = 2, β 2 = −1, θ = 0 ρ = 0, ω = −1, y = 0 and their projections at t = 1,2, 3.
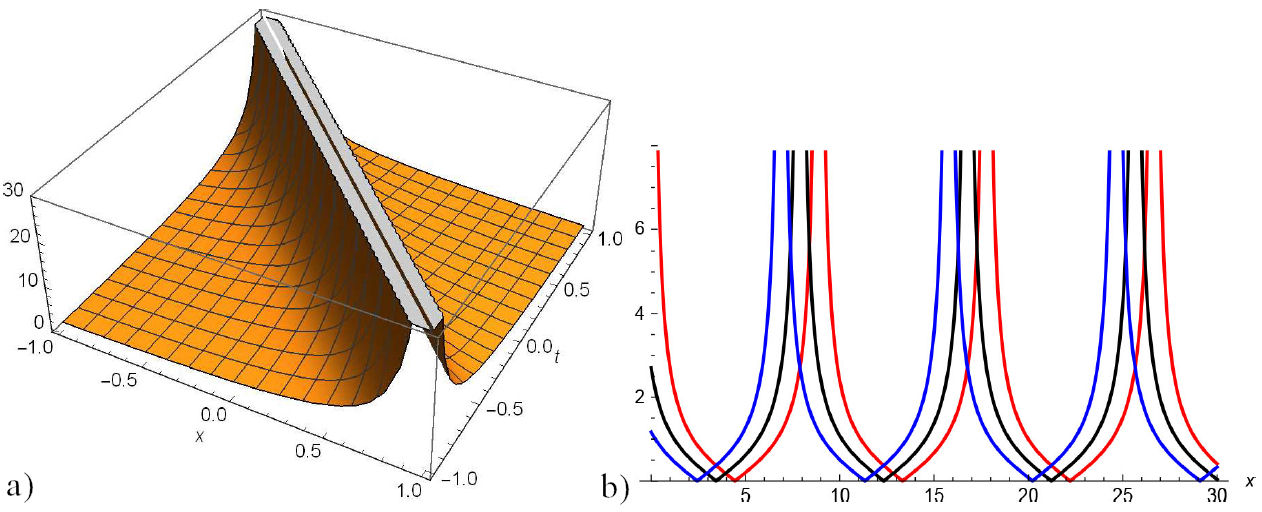
FIGURE 3 a) 3D and b) 2D surfaces of imaginary part of the Φ 3,1 (x,y,t) with −1 ≤ x,t ≤ 1 for the values µ = 1, η = 2.50, λ = 2.50, δ = −1.50, α = 1, α 1 = 1.70, α 2 = 1, β 1 = 2, β 2 = −1, θ = 0 ρ = −4, ω = 1, y = 2 and their projections at t = 0.25,0.500.75.
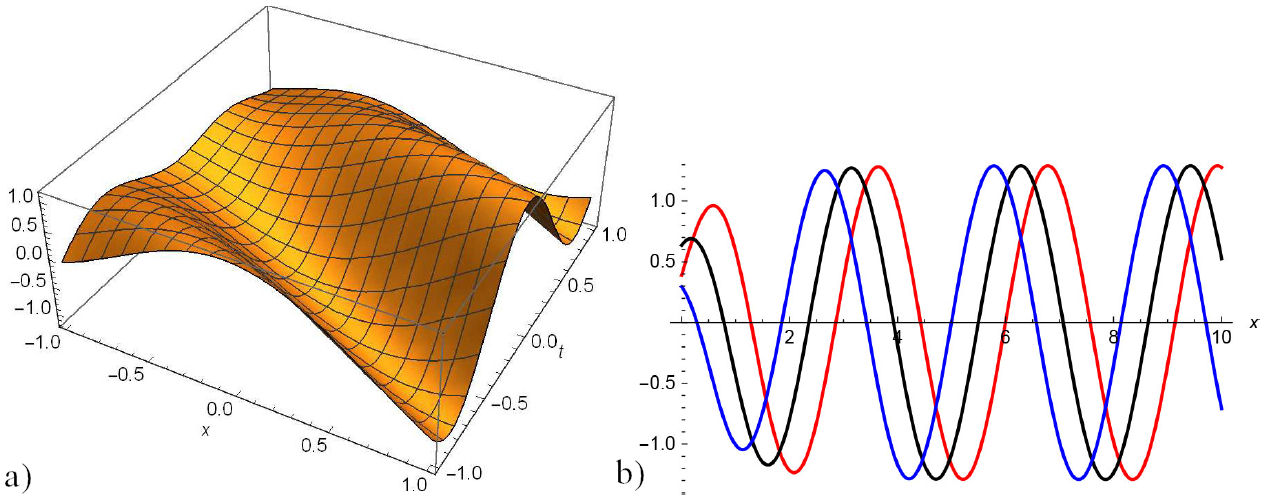
FIGURE 4 a) 3D and b) 2D surfaces of real part of the Φ 3,1 (x,y,t) with −5 ≤ x,t ≤ 5 for the values µ = 1, η = 2.50, λ = 2.50, δ = −1.50, α = 1, α 1 = 1.70, α 2 = 1, β 1 = 2, β 2 = −1.70, θ = 0 ρ = −4, ω = 1, y = −2 and their projections at t = 0.25,0.50, 0.75.
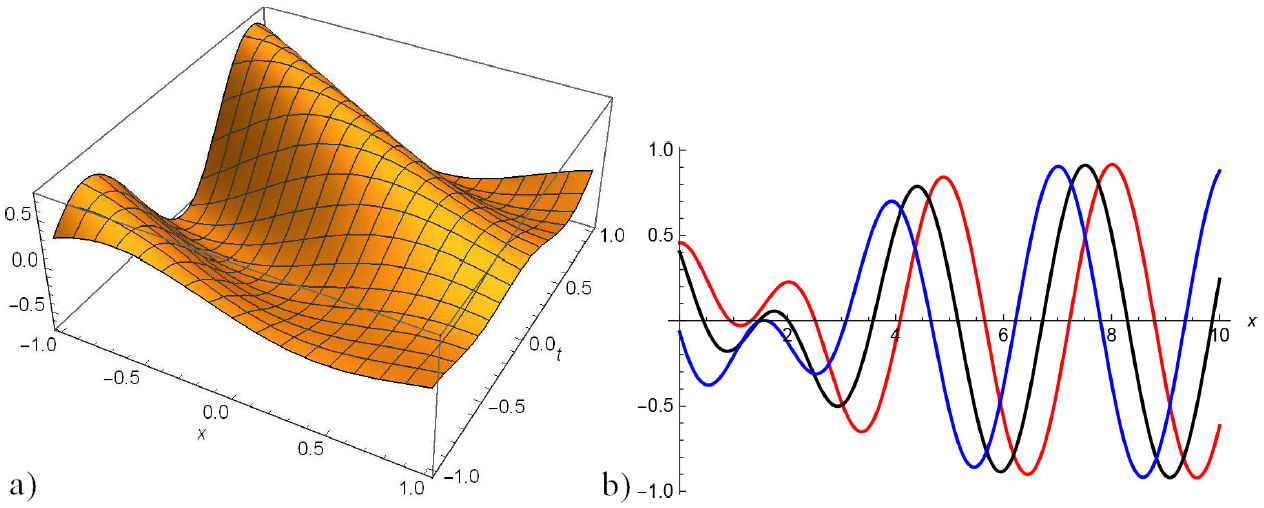
FIGURE 5 a) 3D and b) 2D surfaces of |Φ 3,5 (x,y,t)| with −1 ≤ x,t ≤ 1 for the values µ = 1, η = 2.50, λ = 2.50, δ = −1.50, α = 1, α 1 = −1, α 2 = 1, β 1 = 2, β 2 = −1, ρ = −2, ω = 1, y = 0 and their projections at t = 0,2, 4.
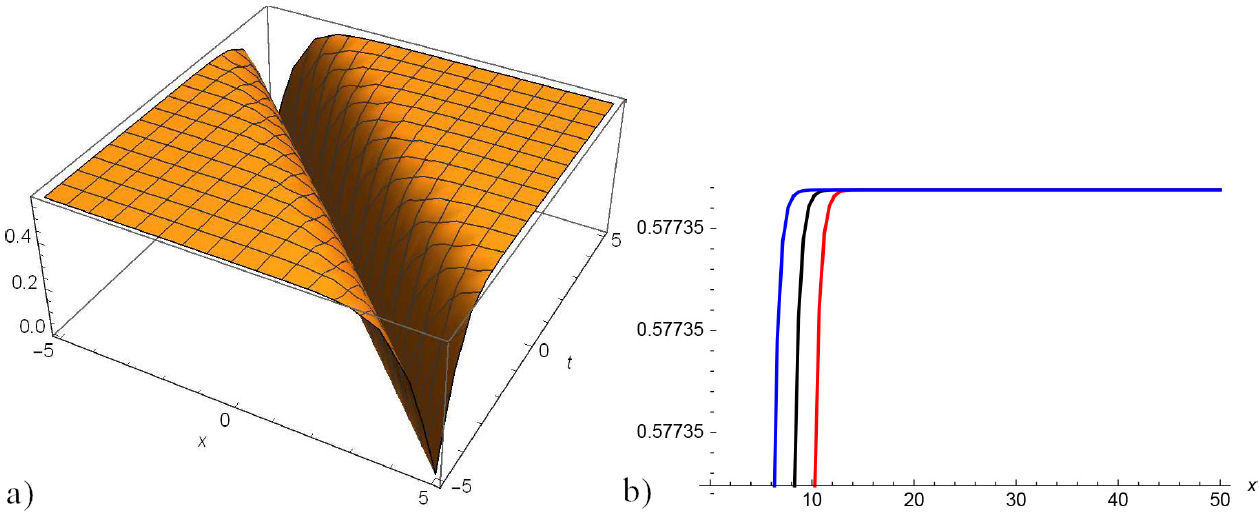
FIGURE 6 a) 3D and b) 2D surfaces of |Φ 4,1 (x,y,t)| with −3 ≤ x,t ≤ 3 for the values µ = 1, η = 2.50, λ = 2.50, δ = 1.50, α = 1, α 1 = 1.70, α 2 = 1, β 1 = −1, β 2 = 1, θ = 0, ρ = −4, ω = 1, y = 1 and their projections at t = 1,2, 3.
4. Concluding remarks
In our work, we have employed suitable technique to develop some new travelling wave solutions to the special kind of nonlinear Schrödinger’s equations. The extended rational sine-cosine method and extended rational sinh-cosh method are found to be as one of the most effective, accurate and powerful tools for the construction of analytical solutions for fractional HFSCs in the semi-classical limit. As a result, obtained some new exact solution in the form of hyperbolic, trigonometric and complex functions solutions. On the basis of our results, we found that solutions presented in [37-39] using different models these solutions will be useful in future development in order to construct exact solutions, the existence criteria of involving parameters are also discussed. Moreover, some of exact solutions obtained by these methods are mostly identical. We can conclude that the proposed method is one of the most proficient techniques and can be efficiently employed for further investigation to NPDEs rasing in contemporary science.











 nueva página del texto (beta)
nueva página del texto (beta)



