2.1. Colloid-colloid (effective) interactions: structural and phase behavior of colloids

Colloids interact with each other via direct forces, such as hard-sphere, electrostatic, van der Waals, and depletion interactions [^3,4], just to mention a few examples. The strength of the inter-particle interaction, as mentioned previously, is of the order of the thermal energy and hence depends strongly on the solution conditions, for example, salt concentration, polymer concentration, pH, etc., but also on external potentials [¹]. This inter-particle interaction determines, among different thermodynamic properties, the internal energy of the whole suspension.

The equilibrium phase behavior of colloidal suspensions is then determined by the delicate interplay between the (internal) energy and entropy. From experimental point of view, that interplay can be easily controlled by means of model colloidal systems [⁵]. Both quantities define the free energy landscape accessible to the colloidal dispersion; this quantity describes the thermodynamic stability of the dispersion and is also the basis for non-equilibrium processes [⁶].

Due to several physical mechanisms, such as slow dynamical relaxation, colloidal particles do not necessarily “self-assemble” into their lowest energy configuration. Then, sometimes, colloids require an injection of a certain amount of energy through external forces to “direct” them into particular structures or assemblies. This process is typically known as directed self-assembly and permits that the structural organization of particles can be fully guided and controlled. Additionally, this degree of control allows us to systematically induce structural transitions. Hence, the use of templates and the application of external fields allow one to change either the energy or entropy landscapes according to which the colloids self-organize to form macroscopic structures with different optical, mechanical, electrical or magnetic properties [^5,7].

2.2. (Indirect) hydrodynamic particle-particle interactions: dynamics of colloids

A typical characteristic of colloidal particles immersed in an aqueous medium is the so-called thermal motion, known as Brownian motion [⁸]. There exist essentially two forces that govern the dynamics of a single colloid: thermal forces induced through collisions with the solvent molecules and the friction force due to the solvent viscosity, which damps the particle motion [⁸].

Many phenomena of colloids resemble those of atomic or molecular systems. However, due to the presence of the solvent, they exhibit special interactions that distinguish them from atoms: the hydrodynamic interactions (HI) [⁹]. Contrary to (direct) particle-particle interactions, HI can be tuned, but never completely screened or switched off. In a simple physical picture, HI can be understood as follows. The motion of a given colloidal particle induces a flow field in the solvent, which is felt by the surrounding colloids, i.e., when a colloid moves, it displaces the fluid in its immediate vicinity [⁹], thus, the motion of one colloidal particle causes a solvent-mediated force on the neighboring colloidal particles. HI lead to non-trivial hydrodynamic coupling among colloids that extends over many mean-interparticle distances [¹⁰]. HI are hence mediated by the solvent and become a particular type of indirect interactions. They affect the dynamical behavior of colloids. In contrast to the static counterpart, the colloidal dynamics is far from being completely understood, although the effects of HI on the dynamical coupling between two colloids or a colloid near a wall have been the subjects of intense research during the last few decades [¹¹]. The reason is partially related with the fact that the colloidal dynamics extends over a wide range of temporal scales due to the enormous difference in size and mass between the colloids and the solvent molecules. The understanding of HI is also of relevance in other branches of science, such as Biology, since phenomena like hydrodynamic synchronization in either biological systems (sperm, cilia, flagella) [^12,13] or active fluids [¹⁴], and the dynamics of microswimmers [^13,14] can only be explained in terms of hydrodynamic coupling.

2.3. Equilibrium phase behavior: gas-liquid coexistence

Depending on the thermodynamic conditions, i.e., temperature and density, and the details of the interaction potential among the constituents (atoms or molecules, but also colloids) of a material, a large diversity of structural transitions and/or thermodynamic phases, for example, liquid-solid (disorder-order), can occur at equilibrium. The way in which such transitions take place is referred to as “phase behavior”.

In particular, the study of the phase equilibrium in colloidal suspensions is of relevance in Physics, Biology and Materials Science [¹], just to mention a few examples. This growing interest resides in the fact that, on one hand, colloidal suspensions are ubiquitous in nature comprising among others milk, paints, mud, additives, etc. Additionally, they are simple model systems that allow us to obtain a better understanding of the phase behavior of more complex or experimentally less accessible fluids, such as protein suspensions or molecular systems.

Protein phase separation is typically of interest in the production of protein crystals, which are used both in pharmaceutical industry and protein crystallography [¹⁵]. Recently, it has been shown that protein phase separation in organic tissues is related with diseases such as cataract [¹⁶], sickle cell anemia [¹⁷], Alzheimer disease [¹⁸], cryoimmunoglobulinemia [¹⁹], among others. Therefore, a complete knowledge of the phase transitions of proteins in suspension may help to develop therapies against such diseases. Additionally, proteins exhibit interesting structural and dynamical properties, such as cluster formation [²⁰] and intermediate order [²¹]. In particular, lysozyme (a globular protein) has been used as model protein to understand the phase behavior of biomolecules in aqueous solutions [²²]. During the last few years, patchybased models have also been used to explain the rich phase behavior of lysozyme, other types of proteins and colloidal fluids, see, e.g., Ref. [²³] and references therein.

Colloidal and protein suspensions show phase separations analogous to the transitions observed in simple liquids. In the fluid-solid transition, the colloidal particles form regular structures (crystals) [²⁴]. In the coacervation or gas-liquid transition of the colloidal suspensions, two fluid phases with different colloidal concentrations coexist [²⁵]. When the range of the attractive interparticle interaction is short-ranged (a few percent of the particle diameter), the gas-liquid transition is metastable inside the fluid-solid transition and, therefore, it is termed a ‘buried’ transition [²⁶], see, e.g., Fig. 1. The research of the gas-liquid transition in colloidal systems with short-range attractive interactions has been motivated by the aim of finding the optimum conditions for nucleation that occurs near to the metastable binodal and of understanding the physical mechanisms behind the dynamical arrest transition in adhesive-like colloidal systems [^27-29].

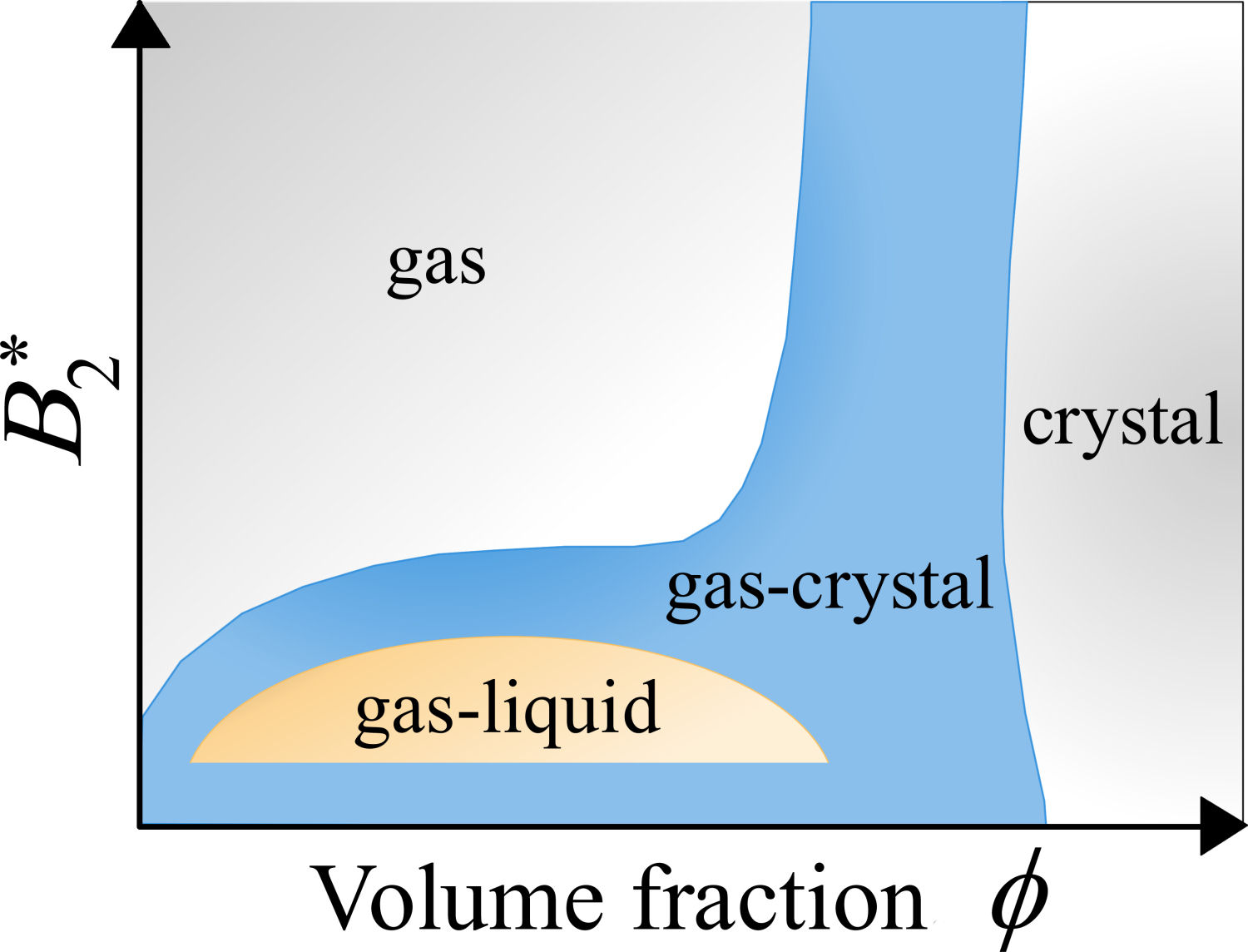
FIGURE 1 Cartoon of the typical equilibrium phase diagram of colloids interacting with a short-range attractive potential [^26,30]. The vertical axis represents the reduced second virial coefficient, B ^* 2= B2/B ^HS 2 , with B ^HS 2 being the second virial coefficient of the hard-sphere fluid. The horizontal axis represents the colloidal volume fraction, ϕ.  

Recently, the phase behavior of protein and colloidal systems has been theoretically studied [³⁰]. In particular, the metastable gas-liquid coexistence was investigated in the regime where the attractive forces between macromolecules are of short-range. As model systems, the hard-core attractive Yukawa and Asakura-Oosawa potentials (fluids dominated by energetic and entropic contributions, respectively) were considered, which were also mapped onto equivalent squarewell potentials of appropriate range, λ, within the regime 1.05 ≤ λ ≤ 1.25. It was confirmed that the coexistence curve is more or less independent of the detailed functional form of the interaction, but just depends on the value of the second virial coefficient, B ₂. Thus, interestingly, different thermodynamic driving forces, i.e., energy and entropy, led to the same phase behavior. The theoretical results were compared against experimental data for lysozyme proteins and obtained excellent agreement. This indicates that although a protein solution is a very complex system, some of its thermodynamic properties can be quantitatively understood in terms of the physics of colloids. This is of scientific and technological importance, since predictions based on simple physical models are beneficial for the design, synthesis and control of processes involving proteins.

2.4. Non-equilibrium thermodynamic states: colloidal gels and glasses

As explained above, at some thermodynamic conditions, many-body systems do not reach their (equilibrium) stable state, i.e., the lowest free energy configuration, and can get trapped in long-lived metastable non-equilibrium states. Examples of those non-equilibrium states are colloidal “gels” and “glasses”. These two states exhibit a solid-like behavior, such as a yield stress, but show a liquid-like (disordered) structure [^27,31]. Furthermore, gels need an attractive component in the interaction potential among particles; nevertheless, in the gel state, particles can still re-arrange their positions due to thermal agitation. On the other hand, glasses occur at high concentrations and can be formed independently of the nature of the interaction potential between particles; when the attraction dominates it is referred to as “attractiondriven glass”, on the other hand, if the repulsion dominates it is called “repulsion-driven glass”.

Colloidal gels are observed in many fields, ranging from Condensed Matter Physics to Materials Science and Civil Engineering (concrete is the prominent example), as well as Biology and Biotechnology and are at the heart of many consumer and food products [^1,2]. However, due to the particular features of each system, we lack a general definition of gelation that allows us to understand, on one hand, the physical mechanisms that give rise to the formation of the arrested states of matter and, on the other hand, the route that connects a gel state with a glass (and vice versa). At low concentrations, ϕ < 0.15, with ϕ being the colloidal packing fraction, gelation occurs inside the gas-liquid coexistence [^27,32]. Below the binodal, percolation is congruent with gelation as observed in numerous studies [^27,32]. The formation of a percolating network, where particles are linked by high-energy bonds (∼ 4 k _B T; k _B and T are the Boltzmann’s constant and the absolute temperature, respectively), provides stability and can modify the elastic properties of the suspension. At intermediate and high concentrations, 0.15 < ϕ < 0.45, percolation is necessary but not sufficient for gelation, as can be observed by comparing the experiments with the exact percolation line computed by Monte Carlo simulations. At higher concentrations (ϕ > 0.45), the attractive glass transition is driven by the balance between the attractive potential and the repulsion due to excluded volume effects [²⁷]. This balance may lead to a large variety of distinguishable non-bonded and bonded repulsive glassy states.

As discussed above, the identification of the physical mechanisms that lead to arrested states of matter, especially gels and glasses, is still one of the major goals in Colloidal Soft Matter Physics. Of course, the complex nature and microscopic details of each particular system are relevant. However, from both scientific and technological viewpoints, a general, consistent and unified description is of paramount importance. The enormous interest in arrested states is basically associated with the fact that these non-equilibrium states of matter exist in nearly every area of our daily lives and are frequently used in both technological and medical applications. However, due to the complex nature and molecular details of each colloidal system, our current knowledge on the origin of both gel and glass states is extremely limited. Hence, it is important to develop appropriate experimental model systems, advanced simulation techniques, and first-principles approaches to describe the most elementary properties of these arrested states.

In a recent analysis of experiments of the dynamical arrest of adhesive hard-sphere (AHS) nanoparticle dispersions [^27,28] by Monte Carlo computer simulations, it was shown that critical gel formation is consistent with rigidity percolation of a dynamic network with a coordination number or average number of bonds <nb>=2.4 [²⁹]. This result is illustrated in Fig. 2 (adapted from Ref. 29), where the new and non-equilibrium state diagram, i.e., reduced second virial coefficient B2*vs packing fraction ϕ, of the AHS dispersion is explicitly shown.

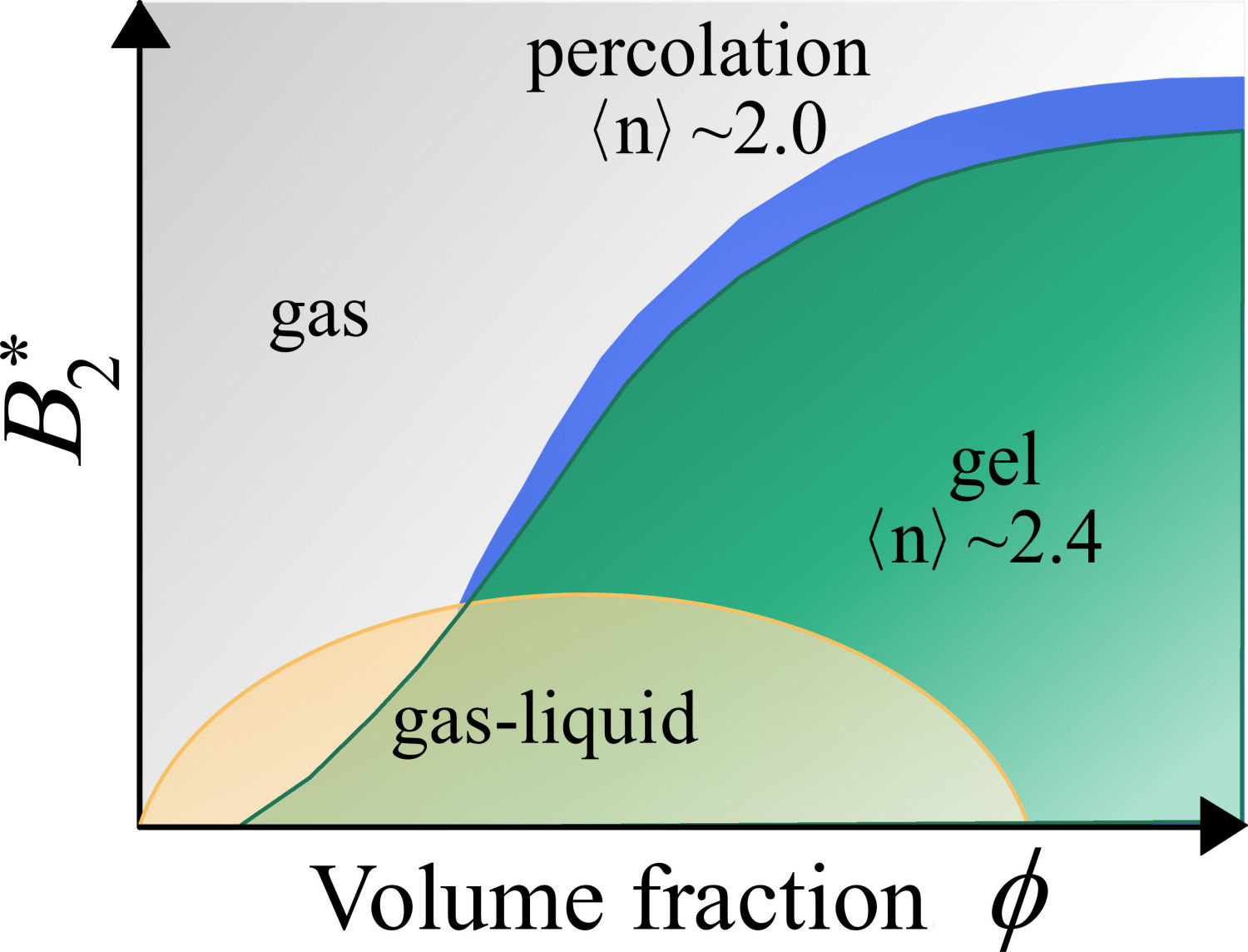
FIGURE 2 Cartoon of the non-equilibrium phase diagram of an adhesive-like colloidal dispersion. Blue region, which starts when the average number of bonds is 2, represents the connectivity percolation. Green area, which starts when the average number of bonds is 2.4, represents the rigidity percolation and is associated with the onset of gelation [²⁹]. The vertical axis is the reduced second virial coefficient, B ₂ ^∗ = B ₂ /B ₂ ^HS , with B ₂ ^HS being the second virial coefficient of the hard-sphere fluid. The horizontal axis denotes the colloidal volume fraction, ϕ.  

Particularly, it was reported that dynamical arrest for AHS dispersions is driven by the same mechanism that leads to rigidity transition in network-forming materials [³³]. This discovery builds toward a consistent and unified description of critical gel formation in systems with isotropic short-range attractions and it may have a very broad applicability for systems of technological relevance. However, the (possible) universality of these findings deserves to be further tested in well-controlled colloidal systems, for example, depletionbased systems, i.e., mixtures of colloids and polymers.

2.5. Directed self-assembly and anomalous transport of colloids

One of the central aspects of Colloidal Soft Matter is its ability to, under certain thermodynamic condition, self-assemble in a large diversity of structures. As we pointed out above, self-assembly can be directed, enhanced, or controlled by either changing the energy or entropy landscapes using templates or applying external fields (created, for instance, by the interference of laser beams; see Fig. 3); an injection of a certain amount of energy through external forces allows us to fully control or direct both structural and dynamical properties of colloidal particles. The way in which such a process takes place is referred to as “directed self-assembly” [³⁴]. Then, an external field, namely, periodic, random, either spatially or temporally correlated, can drive the colloidal dispersion into a completely new stationary state [³⁵]. Thus, directed self-assembly of colloidal dispersions allows one to explore and understand the order-disorder transitions induced by the external perturbation, see, e.g., Fig. 4, and their connection with the slow particle dynamics of more complex systems, namely, supercooled liquids and glasses [^36,37].

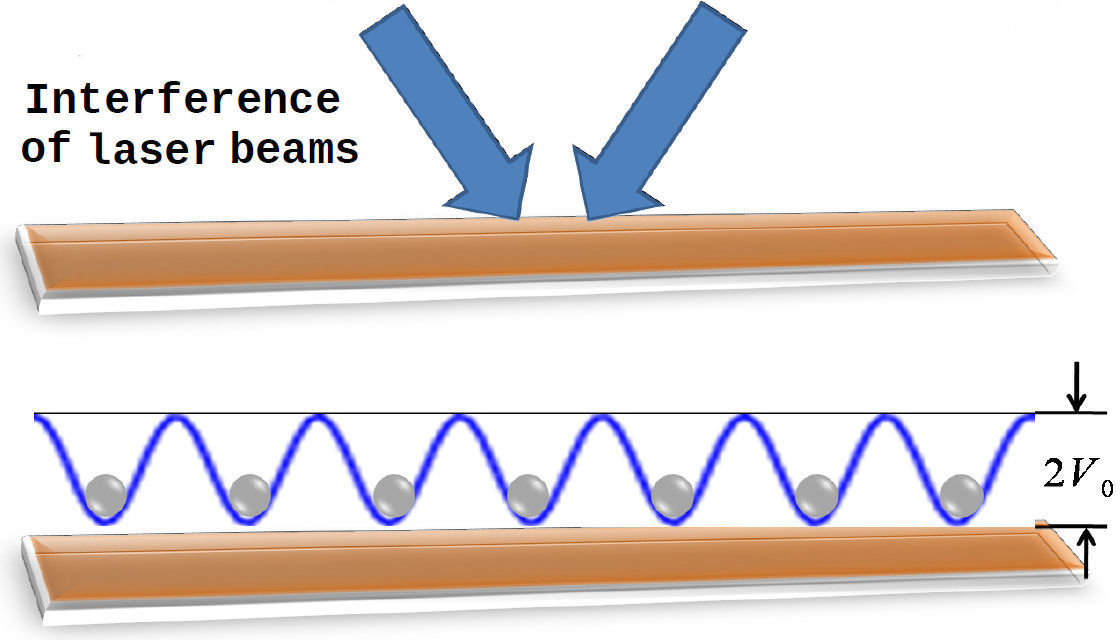
FIGURE 3 Top: interference of laser beams (blue arrows) on a quasi-two-dimensional colloidal sample. Bottom: colloidal particles on the minima of the periodic external field (blue solid line); V ^* 0 ≡ V0/kB T is the coupling between the colloids and the periodic light field.  

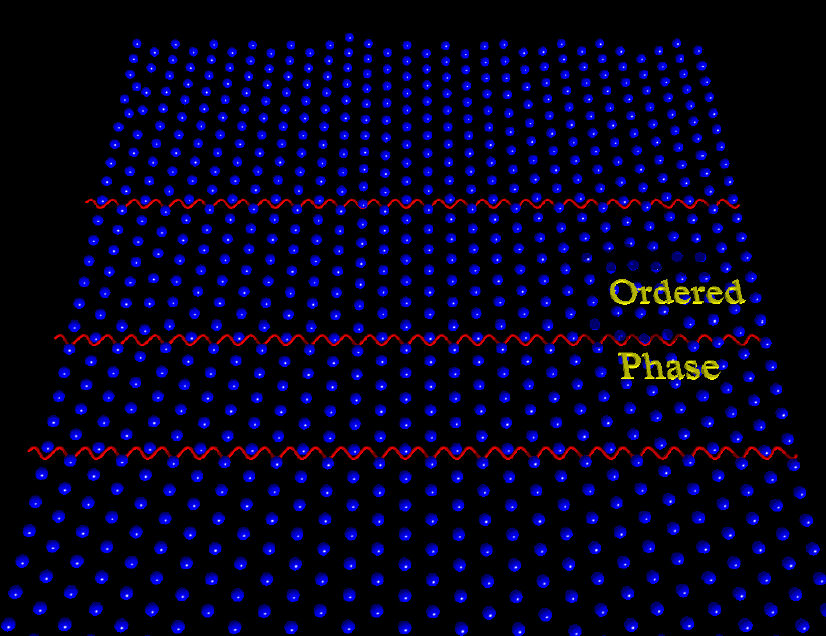
FIGURE 4 Snapshot of the order-disorder transition induced by a periodic external field (red solid line) in a two-dimensional colloidal dispersion.  

Recently, the particle dynamics of quasi-two-dimensional (q2D) colloidal suspensions exposed to both sinusoidal and random potentials has been studied both theoretically and experimentally [^36,37]. In particular, it has been found that the mean-square displacement along the direction of the applied external field is close to the one in a q2D colloidal supercooled liquid [^36,37]. Moreover, single-particle diffusion in random potentials has been studied by means of experiments in systems composed of non-interacting colloids [³⁸]. The experimental results are very similar to recent theoretical reports, where Brownian dynamics simulations also predict three different dynamical regimes [^39,40].

When colloids are confined in narrow channels in such a way that mutual passage is excluded, i.e., 1D-like configuration, the colloid dynamics at long-times becomes ”anomalous”; it deviates from the well-known linear behavior [⁹] and it reaches a dependence that goes as the square root of time∼t [⁴¹], which is the result of the correlation of the particle displacements. This anomalous dynamical behavior is known as single-file diffusion (SFD) and has been the subject of intensive research due to its implications in several branches of science, such as Biology, see, e.g., Ref. [⁴²] and references therein. It has been shown that SFD occurs even when the colloids are subjected to periodic external fields, independently of the commensurability parameter [^39,40,43], p, which quantifies the competition between the number of colloidal particles and the number of minima of the external field along the channel, and the value of the coupling,

V0*≡V0/kBT, between the colloids and the periodic field; see Fig. 5. Interestingly, it was also reported that under the conditions of SFD, a structural transition from a fully disordered state to pseudo-solidlike state in repulsive 1D colloidal systems seems to occur regardless the nature of the potential between colloids. This order-disorder-like transition can be characterized by the main peak of the structure factor or the particle mobility [⁴⁴]; both quantities reach threshold values at the transition.

FIGURE 5 Snapshots of colloidal particles confined in narrow channels and subjected to periodic external fields (solid red lines). p ≡ N _min /N _p is the so-called commensurability factor, with N _min and N _p being the number of minima of the external field and the number of colloids, respectively. V0*≡V0/kBT is the coupling between the colloids and the periodic field.  

2.6. Theoretical frameworks and molecular modeling

As stated in the Introduction, the physical properties of colloidal suspensions can be studied by means of different complementary techniques, i.e., experiments, theoretical approximations and computer simulations. In particular, theoretical frameworks, such as the integral equations theory [⁴⁵], and molecular simulation-based models [⁴⁶] have been developed during the last few years to account for the structure, dynamics, effective interactions and the phase behavior (in and out of equilibrium) of colloids. Furthermore, mean-field approximations have been proposed to study the denaturation processes of bio-colloids [^47,48], i.e., structural changes in macromolecules caused by extreme thermodynamic conditions.

As stressed out above, one focus of colloidal science research is concerned with determining particle-particle effective interactions. More specifically, by means of the multicomponent Ornstein-Zernike equation, a theoretical approximation that accounts for the effective interactions between colloids when part of the system is integrated out of the description has been successfully developed [^49,50]. As we will explain in detail in the following section, this approximation can be used, for example, to determine the phase behavior of a colloidal binary mixture and the depletion forces between large colloids [⁴⁹]. This theoretical approach has been complemented with the development of Molecular Dynamics techniques to extract the effective interactions in mixtures of colloids with large size asymmetries [⁵¹]. Furthermore, by mixing mean-field approximations for charged colloids together with integral equations theory for liquids, it has been possible to determine accurately the effective charge of colloids and to establish a relationship between the latter with the structure of charge-stabilized colloidal suspensions [^52-55].

Also, as pointed out previously, another interest in colloidal science is related to the equilibrium and nonequilibrium behavior of colloidal dispersions. Based on the self-consistent Ornstein-Zernike approximation, the phase behavior of colloids and (model) proteins in suspension can be fully explained [³⁰]. Additionally, Monte Carlo computer simulation methods in different ensembles have been developed to understand, for instance, the structure, morphology and phase behavior of colloids and proteins [^29,30,56,57].

Brownian dynamics simulation schemes that explicitly include hydrodynamic interactions have been adapted to investigate both the structure and dynamics of colloids under the action of external fields (periodic energy landscapes, shear rates, etc.) [^36,39,40,58]. Furthermore, a novel Brownian dynamics algorithm to study the diffusion on curved surfaces [⁵⁹] was proposed; this might be useful to explore the colloidal dynamics in either non-regular or fluctuating surfaces, as we will discuss further below.

2.7. Experimental techniques: Scattering, optical microscopy and optical fields

Since the size of (relatively large) colloids is at least a few hundred nanometers, i.e., about the wavelength of light, the structure and dynamics of colloidal dispersions can be experimentally studied by means of scattering techniques [^60,61], namely, light, x-ray and neutron scattering methods. Single colloidal particles can also be observed by confocal and conventional (optical) microscopy [^11,62]. Furthermore, due to the slow colloidal dynamics, colloids can be followed and thus their trajectories determined on a microscopic single particle level. One can also manipulate individual colloidal particles or ensembles of colloidal particles using light [³⁵]. The development of the so-called optical tweezers has been essential for the manipulation of colloids [⁶³]. Optical traps use the forces exerted by strongly focused beams of light to move and trap individual colloidal particles [^64-66]. Moreover, extended light fields can be applied to exert (almost) any potential energy landscape on colloidal particles [^35,67] (see Fig. 3). They can be used to, e.g., investigate the dynamics of one-dimensional colloidal systems, i.e., single-file diffusion on corrugated substrates [^39,40], as displayed in Fig. 5, to analyze the multiple structural properties on quasi crystalline substrates (as shown in Fig. 4), and to study both the phase behavior and the dynamics of quasi two-dimensional colloidal systems on periodic substrates [^36,58,68,69].

3.1. Effective interactions between colloids near nonequilibrium thermodynamic states

The understanding of the effective interactions between the observable constituents of a colloidal dispersion has been fundamental in Colloidal Soft Matter Physics because it allows us to deal explicitly with the many-body problem, which becomes technically intractable due to the large number of degrees of freedom needed to describe the molecular nature of any material. Basically, effective interactions allow us to treat in a simplified way the description of colloidal systems, which typically posses multiple time and length scales [⁹].

Unfortunately, there is not a unique route to determine the effective interactions between colloids. In fact, several approaches have been proposed to determine the nature of the effective forces and are commonly based on highly demanding computer simulation schemes, sophisticated mean-field approaches and complex theoretical frameworks [^3,4,70]. Additionally, these methods commonly work well at low colloidal concentrations. Furthermore, most of them consider the host medium as a structureless continuum at thermodynamic equilibrium when the separation of its degrees of freedom respect to those from the colloids is well-established. This assumption facilitates the calculation of the effective interaction. From experimental point of view, the situation is even more complicated, since the accurate determination of the effective potential between colloids is practically limited to two colloidal particles, i.e., infinite dilute limit, where the effective potential basically reduces to the so-called potential of mean force [⁴⁵].

Currently, there has been a growing interest to understand the nature of effective forces under non-equilibrium thermodynamic conditions [⁷¹] and close to thermodynamic metastable states [^49,72]. One prominent example is the so-called “critical Casimir force”, which emerges when colloids are put into a host medium that experiences a phase separation [⁷³]. Recently, this kind of effective interaction has been used as an efficient mechanism for the size-selective particle purification of colloidal dispersions [⁷⁴].

Then, the determination of effective interactions between colloids near non-equilibrium states is a new venue with potential technological applications that requires the development of robust theoretical frameworks and efficient simulation-based tools that allow us to account for quantitatively the effective forces between colloids even under conditions far from thermodynamic equilibrium. For example, within the integral equations theory of liquids for the effective interactions, one takes advantage of the covariant property of the Ornstein-Zernike equation when the degrees of freedom of the unobservable components of the fluid are integrated out from the description and are fully taken into account within the effective potential between the observable molecules [^75,76], i.e., colloids. This theoretical approximation represents a good starting point since it has been demonstrated that it quantitatively describes the effective potential among macromolecules when compared with either molecular simulations or experiments [⁵⁰] and can be accurately applied near to non-equilibrium conditions [⁴⁹]. In particular, this formalism has been used to understand the depletion forces between colloids, see, e.g., Refs. [^50,75,76] and references therein, and the effective interactions in chargestabilized colloidal dispersions [⁷⁷].

Applying the same idea based on the “contraction of the description”, a novel computational scheme to calculate the effective forces between colloids has been recently proposed [⁵¹]. This approach is based on the calculation of the total force exerted on a colloidal particle at a given instant in time, and its decomposition on contributions from other close colloids. The main advantage of this approach is that it works well at finite concentrations, so concentration effects can be fully taken into account. Thus, nowadays, there is a clear and straightforward route to study effective interactions between colloids at non-equilibrium thermodynamic conditions and far beyond the infinite dilute limit.

3.2. Depletion forces and gelation in anisotropic colloids

Recently, much of the research on colloidal systems has focused on the development of complex colloidal particles, that is, anisotropic in shape or orientational-dependent interactions [⁷⁸]. Among them, clusters formed by assembling hard spheres represent the first step in the direction of a new colloidal model system [⁷⁹]. Preliminary investigations have demonstrated the formation of colloidal clusters or aggregates and studied their translational and rotational diffusion properties [^80-82]. On the other hand, its phase diagram has not been fully determined and the form of the depletion forces that can be induced by either polymers or other colloidal components of different sizes has not been investigated in detail. The question that remains to be answered is associated with the effect that anisotropy has in the form of the attractive interaction potential due to depletion effects and the presence of a sufficiently large attraction. The internal structure of the aggregates that can be formed due to the strong attraction between (non-spherical) colloids imposes limits on the possible types of bonds and, therefore, in the formation of gel-like networks; this results in new forms of colloidal gels [⁸³]. The resulting new non-equilibrium states will also depend on the cluster morphology, that is, they will possibly be different for dimers, trimers, tetramers, and so on. So, it becomes interesting to reveal new forms of self-assembly for anisotropic colloidal dispersions.

3.3. Chemical regulation mechanisms and effective interactions between charged colloids

One of the most important aspects and challenges of the physicochemistry of macromolecules in suspension is the determination of the effective interactions between the former and the thermodynamic properties of the suspension, since due to its electrostatic nature and the fact that any suspension stabilized by charge is constituted by a large number of charged species that have different characteristic length and time scales, the description of this kind of colloidal dispersion becomes a very complicated task. In the best scenario, one has resorted to theoretical mean-field schemes and to light and neutron scattering experiments that have made it possible to quantify, approximately, some of the physical properties of the suspension [^52,54,84-86], but which, unfortunately, have not allowed us to include the contribution of all species in determining the physicochemical properties of this type of colloidal material. However, recently, a computer simulation approach [⁵⁵] and a formalism based on the theory of integral equations of simple liquids [^87,88], which allows one to explicitly include the mechanisms of chemical regulation and the contributions of micro-ions that participate in the electrostatic shielding between charged macromolecules, have been developed. These approaches will allow us to understand, for example, the equation of state and the effective potentials that arise in the case of chargestabilized colloidal suspensions composed of non-spherical macromolecules; colloidal systems that have a high scientific and technological importance.

3.4. Directed self-assembly of functional nanoparticles

Within the field of Nanotechnology, functional nanoparticles, that is, nanoparticles synthesized to make them interact with anisotropic potentials (for example, “patchy colloids”), are one of the most prominent candidates for technological applications [²³]. Self-assembly has been identified as an important process where the elementary blocks that make up the materials spontaneously organize themselves into ordered structures according to the thermodynamic conditions or other constraints (physical, chemical or biological) of the material. However, in order to successfully exploit the self-assembly of nanoparticles in technological applications and ensure efficient rescaling at mesoand macroscopic scales, a high level of direction and control is required through the application of substrates or external fields that can change the valleys or energetic and/or entropic landscapes accessible to nanoparticles [^35,36,39,40]. To this end, it is important to carry out experiments (light scattering and confocal videomicroscopy), computer simulations (Monte Carlo and Brownian dynamics) and theoretical approaches (integral and functional density equations) to understand the processes of directed self-organization and transport of functional nanoparticles (“patchy colloids”) in periodic fields and both spatially and temporally correlated fields.

3.5. Transport of colloidal particles in biological media

Passive transport phenomena in biological media are of great importance: they are associated with the functions developed by proteins in cells and with the transmission of diseases, among others [⁸⁹]. Biological media are complex, made up of many components and heterogeneous in structure, and typically the transport of particles, molecules or biological material through them is anomalous, that is, it does not correspond to a simple diffusive phenomenon [⁹⁰]. Many studies have been dedicated to investigate this type of particle transport, but without elucidating the relationship between the anomalous dynamics and the structural heterogeneity of the host environment and its dynamical evolution. This is in part due to limitations of experimental techniques. However, recently, a technique called “differential dynamic microscopy” (DDM) has been adapted [⁹¹]; it allows one to be very selective in the study of dynamics through the use of fluorescence, and at the same time it provides us with information on the characteristic length scales of the particle dynamics. From experimental point of view, using this technique it is possible to establish a relationship between anomalous dynamics and the characteristic length scales of heterogeneity in biological media. In particular, one can study collagen networks as a biological medium: these networks constitute a large part of the extracellular matter, and can also be used to encapsulate drugs. Then, it is possible the study the transport of colloidal particles through these networks with the DDM technique, varying the conformation of the collagen matrix to obtain different sizes of pores in the network and different degrees of rigidity of the matrix.

3.6. Colloidal soft matter Out of equilibrium

One of the most important challenges in Colloidal Soft Matter Physics is to understand the mechanisms that give rise to the non-equilibrium states of matter. Although there have been important contributions in the particular case of colloidal gels and glasses [^27-29,92-98], it has not yet been possible to understand and establish the relationship between these states of matter [^28,99], or even more, it is important to explore the possibility of introducing a universal definition of gel [²⁹] and, in addition, it is necessary to quantify the effects that the gravitational field has on the formation of non-equilibrium states [¹⁰⁰]. As mentioned above, it is also interesting to study the effective potentials between macromolecules near the gelation or vitrification boundary. To answer these questions, one should carry out experiments with colloidal model systems (mixtures of colloids and polymers or binary mixtures of hard spheres) and to compare the experimental results with those obtained through advanced molecular simulations and accurate theoretical models, such as the mode coupling theory and the self-consistent generalized Langevin equation [⁹⁸].

3.7.Active colloidal matter

Colloidal soft matter is also known as “passive matter”, which exhibits rich equilibrium and non-equilibrium behaviors even in thermodynamic isolation [³¹]. However, open colloidal systems may sustain non-equilibrium dissipative structures [¹⁰¹], while other systems or materials made up of units that constantly consume energy from the environment turn it, most of the time through complex mechanisms, into locomotion [¹⁰²]. Flocks of birds, molecular motors and layers of vibrating grains fall in this category because they all extract energy from their surroundings at a single particle level and transform it into mechanical work using different phoretic mechanisms [¹⁰³]. By studying the individual behavior of self-propelled particles, i.e., self-propelled or active Brownian particles and microswimmers, and the collective behavior that emerge in systems of interacting active colloidal particles, the understanding of the non-equilibrium nature of this “active matter” can be enhanced, and thus fundamental first-principle frameworks for investigating the Statistical Physics of Out-of-Equilibrium systems can be built. More importantly, it is possible to adapt well-established theoretical formalisms to the case of active matter to account for the most elemental properties of dissipative matter and the non-equilibrium transport and self-assembly of materials composed of active colloidal particles, see, e.g., Refs. [^92,104-108]. Undoubtedly, this is one of the most difficult problems, from conceptual point of view, and of greater scientific challenge that Colloidal Soft Matter Physics will face in the following decades.

3.8. Non-equilibrium state diagram and active microrheology in DNA-decorated magnetic colloids

Soft colloidal dispersions have important applications in different biomedical and industrial fields, for example, as materials for the realization of lenses, or as agents for the transport of medicines. Recently, a new class of soft colloids was developed and they consist of rigid particles, which can be latex, superparamagnetic or gold nanoparticles, which are coated with long DNA chains, so that the DNA crown occupies the majority of the volume of the particle [¹⁰⁹]. The most innovative property of these particles is the ability to deform under conditions of high concentration without the crowns of the particles being penetrated: This characteristic, due to electrostatic and entropic interactions, makes the friction between the particles small also under conditions of high packing and avoids dynamical frustration phenomena that lead to the formation of non-equilibrium states in other systems, such as star polymers [¹¹⁰]. These characteristics allow, in principle, the formation of peculiar crystalline states with a high degree of packing and anisotropic conformations of the particles [¹¹¹] that have not been observed experimentally yet. On the other hand, the deformability characteristics of these particles can be important in active transport phenomena, that is, the transport of this type of particles in a host medium by means of an external field, for example, a magnetic field for paramagnetic colloids. These phenomena are of interest in the transport of drugs in the human body and constitute a way of measuring the non-linear rheological properties of the host environment [¹¹²]. The deformability of the particles is of particular interest in conditions of high concentrations, in which the particle can adapt its shape to facilitate its path through a medium saturated with other particles. Directed transport in highly concentrated media has important implications for phenomena, such as crowding dynamics or protein transport in the cellular environment.

3.9. Universality of the extended law of corresponding states

The idea of having a new thermodynamic metric that allows one to express thermodynamic quantities, such as the equation of state, onto a master curve regardless the molecular details of each particular system has its origins in the pioneering work of van der Waals with the so-called law of corresponding states, see, e.g., Ref. [¹¹³]. However, within the context of colloidal soft matter, this idea was reconsidered by GilVillegas et al. [¹¹⁴], who proposed that the thermodynamic properties of colloidal fluids can be written in terms of the equation of state of an equivalent system used as reference. The equivalent fluid is formed by particles interacting with a square-well (SW) potential whose properties are known accurately [¹¹⁵].

In a similar spirit, the so-called extended law of corresponding states, introduced by Noro and Frenkel [¹¹⁶], valid for systems made up of colloids that interact with very short-range attractive potentials, has been applied as a kind of thermodynamic metric to understand the microstructure and thermodynamic properties of a large number of physical systems, particularly of those close to the gelation or the dynamical arrest region [^27,32]. Recently, it has been shown that it is possible to apply it not only to understand the topology of the phase diagram of model systems [³⁰], but to establish an inverse protocol that allows one to describe the molecular properties of systems as complex as those of proteins [^57,117]. Furthermore, there exists evidence that this extended law can also describe the reversible aggregation mechanisms of colloidal systems interacting with purely attractive potentials [¹¹⁸]. However, it is interesting to see whether it can also describe the aggregation processes in systems where molecules interact with competing potentials, or to show its generalization for the topology of the phase diagram of other types of proteins, including also the dynamical properties of the latter. If the application of this “extended law” is corroborated by carrying out experiments with proteins and both theoretical calculations and computer simulations, we will be faced with the possibility of establishing its “universality” to describe the local, dynamical, global properties and the topology of the phase diagram of that type of colloidal matter where its constituents interact with attractive short-range potentials. This definitely will allow us to establish a new thermodynamic metric in the colloidal domain.

3.10. Fractal dimensions in colloidal soft matter physics

Recently, it has been proposed, for the first time, the existence of concentrated liquids in non-integer dimensions (fractals) that possess non-integral physical characteristics and properties observed in standard spatial dimensions [¹¹⁹]; one-, twoand three-dimensional. The existence of mesoscopic systems in fractal dimensions opens a completely new field within the Colloidal Soft Matter Physics, since it is now relevant to investigate in detail the structural, thermodynamic, transport, and dynamical arrest properties of those mesoscopic materials that exist in fractal dimensions. This is, without a doubt, one of the topics of greatest relevance and scientific challenge of this field, but which, undoubtedly, will define a new scientific agenda and will allow us to generate new knowledge of great impact for Condensed Matter Physics. It is then interesting to carry out a study that combines theory with simulations and experiments, in order to investigate the phase behavior in and out of equilibrium, and the transport properties of mesoscopic particles in fractal dimensions. Two examples of fractal liquids with relevance in industrial applications are emulsions confined in porous media (such as oil-inwater emulsions within the reservoir rock), and electrolytes between porous electrodes in high-performance electrochemical charge storage devices.

3.11. Colloidal soft matter physics and geometry

Diffusive processes are a class of general phenomena that occur in several fields of Physics, including Elementary Particle Physics, Special and General Relativity, and Condensed Matter Physics [^120-123], with Colloidal Soft Matter Physics being a subfield of the latter. Actually, one of the hallmarks of colloids is their ability to diffuse [⁹]. In the last few decades, there has been great interest in the study of diffusive phenomena on curved surfaces motivated, mainly, by problems from Biophysics, such as the transport of proteins [¹²⁴].

Within the context of Soft Matter Physics, the curved varieties arise as the emergent result of the collective interactions between molecules that make up the material, for example, the interactions between amphiphilic molecules immersed in an aqueous solution give rise to the formation of vesicles. Analogously, interfaces of soap, polymers, thin channels, even 2D atomic materials, such as graphene, germanium, silica, among others, can spontaneously be formed. All these forms of materials can be represented as mathematical surfaces embedded in a 3D space. The curvature that characterizes these materials represents a kind of external field that affects the particle transport processes. For example, the diffusion of proteins on the cell membrane or the dynamics of biological motors along filaments [¹²⁴].

The inclusion of the geometry or curvature on the diffusion of colloidal-like particles is a non-trivial task. Actually, it represents a formidable physical and mathematical challenge. However, Castro-Villarreal proposed the generalization of the Smoluchowski equation on curved spaces, where the influence of invariants formed with the Riemann curvature tensor on the mean-square displacement was explored [¹²⁵]. Furthermore, Castro-Villarreal also proposed different geometric observables to measure the displacement of a Brownian colloidal particle [¹²⁶]. In particular, it was shown how the geodesic mean-square displacement captures the intrinsic elements of the manifold, while the Euclidean displacement captures extrinsic information from the surface. These results can be generalized to the situation where the Brownian particles interact not only due to the intermolecular potential, but also due to geometrical mechanisms originated from the curvature. From this approach, it was possible to derive the equation of motion of diffusing particles in curved spaces. In particular, a generalized Ermack-McCammon algorithm was developed to study a broader class of transport phenomena in heterogeneous environments [⁵⁹]. All these results have been generalized to the motion of active Brownian particles [¹²⁷], where the mean-square geodetic displacement captures the relationship between the curvature and the activity of the active colloid. In particular, the dynamics of an active Brownian particle on a spherical surface was studied and it was found a dynamical phase transition between an oscillatory behavior and a monotonic one within the random behavior of the active particle [¹²⁷].

The aforementioned ideas and proposals to elucidate the particle transport in non-Euclidean spaces have been partially and recently corroborated in experiments of polystyrene nanoparticles diffusing on highly curved water-silicone oil interfaces [¹²⁸]. However, further experimental and computational studies are needed in order to better understand the rich diffusion mechanisms that emerge in colloidal dispersions when the curvature plays an important role.

3.12. Competing interactions and reversible colloidal aggregation

Typically, colloidal particles immersed in an aqueous medium interact with an effective potential that has the following features: a strong repulsion at contact that forbids particle overlap followed by a short-range attraction (van der Waals-like interaction) and a long-range repulsion (electrostatic double layer force). This potential is known in colloidal science as the DLVO potential [¹²⁹]. The competition between the short-range attraction and the long-range repulsion in the DLVO potential defines the thermodynamic stability of the colloidal dispersion [^1,129].

Nowadays, there are several ways to tune the (effective) interaction between colloids in order to make more evident the competition between the attractive and repulsive forces in the pair potential [^3,4,70]. This competition not only affect the stability of the dispersion, it can also lead to thermodynamic states where locally the colloids form a family of (reversible and irreversible) aggregates or clusters with a well-defined morphology and degree of compactification [^130-133]. These features can be determined through the parameter known as fractal dimension, d _f , and is typically extracted from the physical quantity called radius of gyration, R _g (s), which represents the effective radius of an aggregate composed of s particles, see Fig. 6. Particle aggregation or clustering is an obligatory step for the initiation of the phase separation or the large-scale formation of materials that exhibit a heterogeneous structure, such as gels and porous media [^132,133]. Nevertheless, even though the macroscopic structure of such materials depends on the shape and size of the resulting clusters or aggregates, the cluster formation at equilibrium and its corresponding morphology are not fully understood. The local morphological information is also important for the identification of the physical mechanisms for arrested states of matter, especially gels and glasses, which remains a hotly debated research topic in Colloidal Soft Matter Physics.

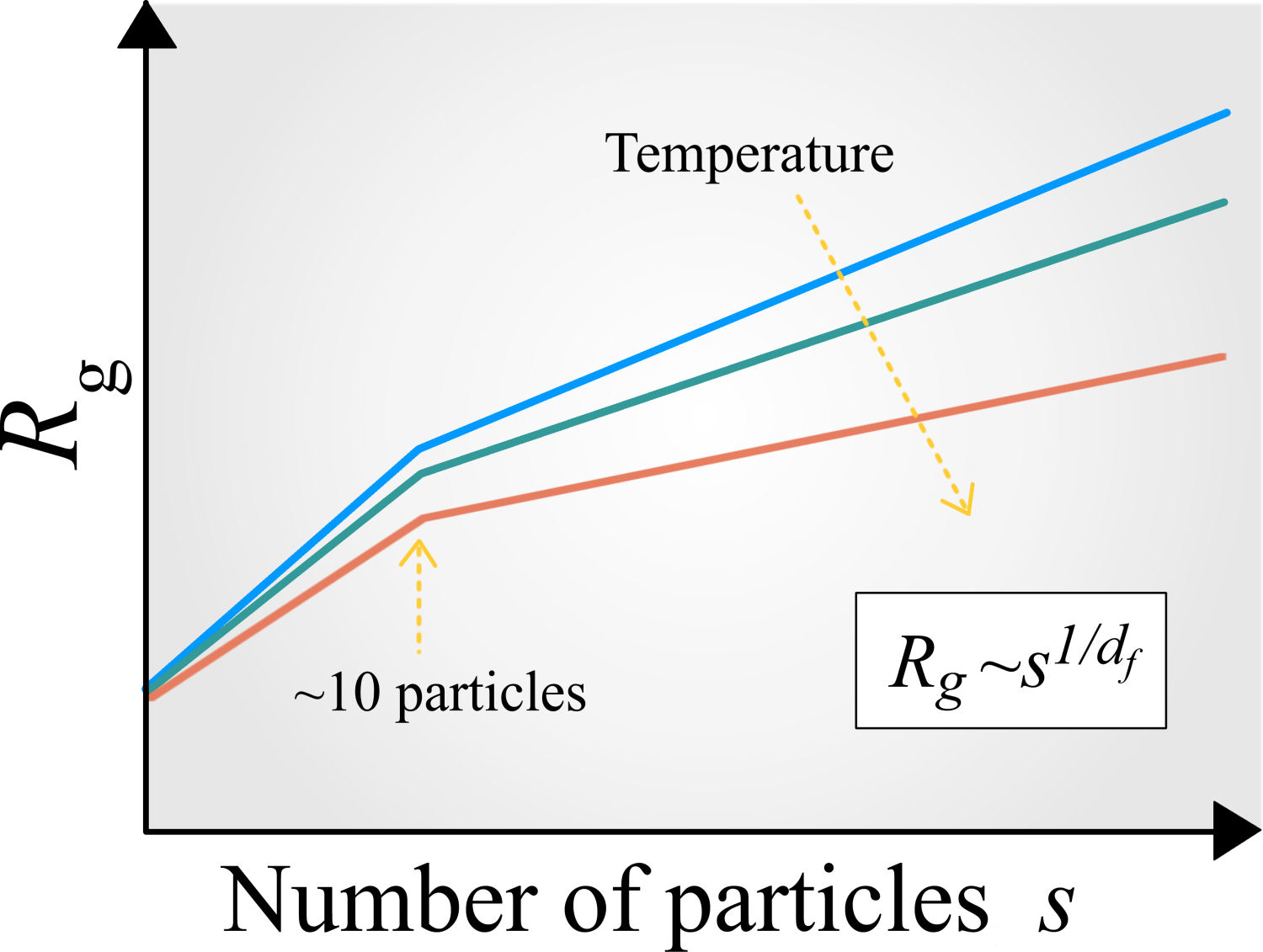
FIGURE 6.Cartoon of the typical radius of gyration, R _g , that characterizes the effective radius of a colloidal aggregate composed of s attractive colloids. This quantity can be used to extract the fractal dimension of small and large aggregates using the relationship Rg ∼ s^1/df [¹¹⁸].  

As mentioned in the previous paragraph, during the last few years, there has been a hot debate about the main mechanisms that determine and define the state of colloidal aggregation, see, e.g., Ref. [¹¹⁸] and references therein; a topic of interest that will allow us to better understand, for example, the transport processes that occur during drug delivery [¹³⁴]. In the particular case of colloids interacting only with shortrange attractive forces, it was found that the fractal dimension, d _f , is completely determined by the second virial coefficient [¹¹⁸], linking then the reversible colloidal aggregation with the aforementioned extended law of corresponding states (ELCS). In the case of competing interaction colloidal fluids, the situation is more complex and the connection with the ELCS is not evident [¹³⁵]. Snapshots of the clusters that can be found as a function of the repulsion strength, A, of the competing interaction potential are shown in Fig. 7. From the snapshots, one can notice how the size and morphology of the clusters depend strongly on the competition between both attraction and repulsion contributions in the pair potential; see Ref. [¹³⁵] for more details.

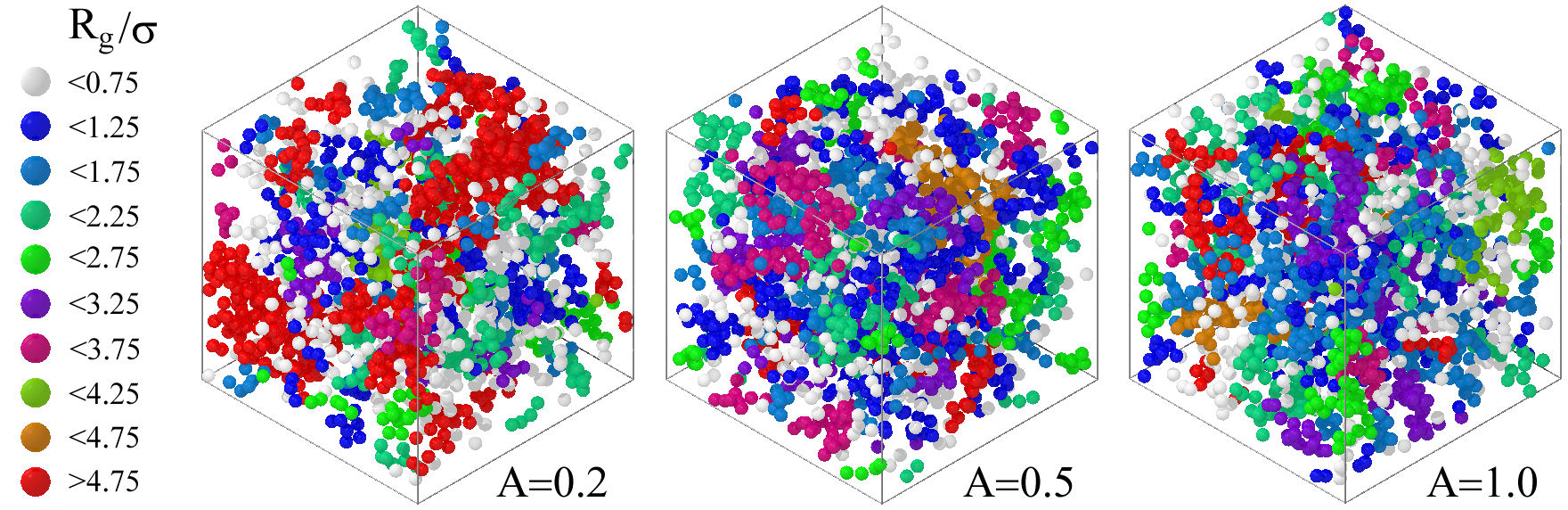
FIGURE 7 Cartoon of the typical clusters that appear in a competing interaction colloidal fluid as a function of the repulsion strength, A, of the competing interaction potential. R _g /σ is the normalized radius of gyration, with σ being the diameter of the colloids.  

A pair potential with the features described above, i.e., a short-range attraction followed by a long-range repulsion, is also known as a SALR potential [¹³²]. Most of the properties of a fluid whose constituents interact with this kind of potential have been mainly studied in monodisperse systems, however, the addition of a second species brings interesting features not typically seen in a SALR fluid. Thus, one not only deal with the competition at the level of the interparticle potential, now one has to take into account the competition between different length scales. As a result, one can find that, for example, the clustering behavior in this asymmetric mixture is controlled by the cross-interaction between the two types of colloidal particles [¹³⁶]. Thus, one can control the resulting degree of aggregation by simply tuning the size asymmetry of the suspension. This phenomenology should also have important consequences on the dynamics of the aggregates.

Finally, we should mention that although the structure and the reversible aggregation in competing interaction fluids seem to be better understood [^132,133], the connection with the transport properties and the role of the hydrodynamic interactions on the mechanisms of aggregation deserve to be studied in more detail. This is of important for technological applications, since most of the biomolecules in an aqueous medium behave as competing interaction fluids [^132,133].

3.13. Analogies between granular and colloidal matter

Colloids and granular media are aggregates of matter that typically exemplify the differences between systems in and out of thermodynamic equilibrium, respectively. Despite the differences in size and in their phase behavior, there are many similarities between the phenomenologies of both systems, for example, they exhibit very similar dynamics [¹³⁷] and rheological properties [¹³⁸] and it is even possible to determine effective potentials between grains [¹³⁹], which allows us treating them with the same or very similar theoretical and computational modeling tools. A crucial characteristic of granular matter, and one that makes it different from equilibrium thermodynamic systems, is the high dissipation of energy when its particles interact at contact. This generates a large diversity of phenomena that make its behavior more difficult to study. However, given the evidence of the existence of a large number of phenomenological similarities between colloidal systems and granular media, it is important to determine which theoretical tools can be used to study both classes of systems simultaneously and to clearly distinguish which phenomena are unique in each domain. Furthermore, a new non-vibrating granular system has been introduced [^140-145] and it is an ideal experimental model system to face the analogies with Colloidal Soft Matter. Thus, using the fact that the latter is perfectly described with the tools of Statistical Physics, one should determine how far these schemes can be extended to the granular domain.

3.14. Colloidal hydrodynamics

The idea that the effects of hydrodynamic interactions (HIs) on the diffusion coefficient of colloidal particles can be decoupled and factorable was proposed 30 years ago by Medina-Noyola [¹⁴⁶]. In his proposal, Medina-Noyola assumed that the long-time diffusion coefficient can be decomposed into two contributions: one associated with the shorttime dynamics (which contains all hydrodynamic effects) and another that depends solely on the direct interaction between colloidal particles. This proposal, widely accepted and used for three decades, has been put under the experimental scrutiny [¹⁴⁷] finding that, although the idea of factoring the effects is correct, the long-time diffusion coefficient does not seem to depend, surprisingly, on the HIs in a two-dimensional system. Similarly, in a recent theoretical-experimental contribution, the dynamics of short times in mixtures of spherical and non-spherical particles has been studied [⁸¹]; the results suggest that the dynamics of short times in asymmetric mixtures can also be uncoupled and factored in terms that depend on the HIs and the direct interactions between the molecules. It is therefore interesting to understand the connection between the dynamics of short times and those of long times [¹⁴⁸], since they determine many of the dynamical processes that give rise to the non-equilibrium states of matter. Thus, it is crucial to carry out a theoretical-experimental study to establish the relationship between these dynamics in, for example, spherical and non-spherical colloidal systems.

In the short-time regime [⁹], the transport coefficients in colloidal suspensions, such as the diffusion coefficients at different length scales and the effective viscosity of a suspension, are entirely determined by the HIs between the colloidal particles. The precise and computationally efficient inclusion of HIs in approximate theoretical schemes or simulations represents a formidable challenge to date: The most complete theory of short-time hydrodynamic interactions in colloids is based on a renormalized fluctuation expansion that was originally introduced by Beenakker and Mazur [^149,150], and which has been recently re-adapted [^151-153]. The modifications allow one the application of the theory in the case of charged colloidal particles and polydisperse systems with different hydrodynamic radii. However, a significant further development of the theory is necessary to allow its application also in the case of particles with different shapes, and in the case of colloidal particles under severe confinement.

3.15. Machine learning and colloidal soft matter physics

Colloidal Soft Matter Physics has been significantly impacted by the current development in Machine Learning (ML) [¹⁵⁴]. Methods ranging from computer vision, feature engineering, classification tasks and many others have been successfully applied to the characterization and description of several colloidal systems. These areas are highlighted in the diagram displayed in Fig. 8. The most important aspect of deploying ML methods to colloidal systems is having a set of features that correctly represent the physical properties of the system itself. These features must have a representative structure such that conventional ML methods can be readily applied to the data set. One such example is the work by Boattini et al. [¹⁵⁵], where a feature set composed of bond orientational order parameters was used, together with a dimensionality reduction algorithm called an autoencoder [¹⁵⁶], to perform automatic discovery of local structural motifs in colloidal systems. Once features have been set, engineered, or discovered for a given system, the task one wishes to solve depends entirely on the physics of the system itself.

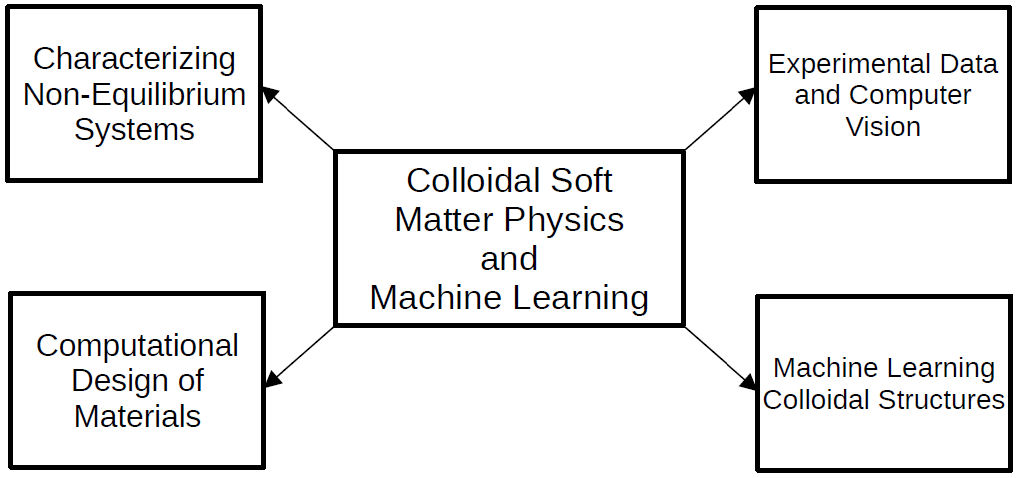
FIGURE 8 Schematic diagram that highlights the intersections between Machine Learning and Colloidal Soft Matter Physics.  

Whether we want to characterize colloidal systems directly from experimental data [¹⁵⁷], or we wish to discover new correlations in non-equilibrium systems such as glasses [^158-160], ML methods have proven useful in these and other important aspects of colloidal matter research. Although very successful, ML methods require large quantities of data, with important features from the studied systems, and these are some of the main disadvantages. Having to deal with massive amounts of data is still a challenge that needs to be solved if these methods want to see mainstream applications. Nevertheless, two important uses of ML methods can be recognized for colloidal systems. One of them is the ability to use a robust and novel ML method that can deal with difficult tasks. On the other hand, some other research groups aim at investigating the model itself, and more classical models haven been used to understand the true nature of colloidal matter. For a more in depth view of this fertile research area we point the interested reader to a recent review on soft matter [¹⁶¹], and to a related review where colloidal active matter is the main topic of discussion [¹⁶²].