1. Introduction
Studies on fractional differential equations have recently increased to model some complex phenomena more accurately. There are many different definitions of fractional derivatives in literature. Some of them are the Caputo derivative [1], the Caputo-Fabrizio derivative [2], the Riemann-Liouville derivative [1], Jumarie’s modified Riemann-Liouville derivative [3], and Atangana-Baleanu derivative [4]. Fractional partial differential equations (FPDEs) have been used in various areas such as physics, control theory, biology, mathematical physics, applied mathematics, optics, chemistry [5-10].
In this article, two reliable methods have been applied to reach the exact solutions of the fractional Phi-4 equation with Atangana’s beta-derivative. One of the methods is the functional variable method [11-12] and the other one is first integral method [13-14]. In some applications in literature, various techniques have been applied to FPDEs [15-26].
The paper is organized as follows: Some basic definitions and properties of Atangana’s beta-derivative are introduced in Sec. 2. In Sec. 3, the functional variable method and the first integral method are examined in detail. In Sec. 4, methods are applied to the fractional Phi-4 equation to obtain some new exact solutions. The final section includes a conclusion containing all outputs in this article.
2. Definition of Atangana’s beta-derivative
Definition 1: Let h : [0,∞) → R be a function. Then its fractional conformable derivative of h order α is,
Khalil et al. defined the above theorem for the fractional derivatives [27].
However, there are similar features between conformable fractional derivatives and ordinary derivatives. For instance, the product derivative and the quotient derivative of two functions. Thus, mathematicians, physicists, and engineers have made many studies on conformable derivatives [28]. Definition 2: Atangana’s beta-derivative is as following
Atangana’s derivative allows us to remove some weak properties of the conformable derivative. For example; A differentiable function’s derivative is equal to zero at the zero points [29]. Thanks to beta derivative, real-world problems which arise in applied mathematics and physics are modeled more accurately. Thus, the physical behavior of the graphics can be interpreted more precisely.
Atangana’s derivative can be preferred because it provides the maximum properties of the fundamental derivatives. Some important features for Atangana’s beta derivatives [30]:
Let us take h 6= 0 and g are two function differentiable with β-order and β ∈ (0,1]. Then
For any d ∈ R. Then,
Using Eq. (2), ε = (x + (1/Γ(α))) 1−α f, if ε → 0 then f → 0. The Eq. (7) has been obtained.
and
where γ is a constant. Finally, we can write the following equation
3. Description of methods
3.1. Functional variable method (FVM)
A brief description of the suggested method:
Step 1. FPDE can be written in the form:
Step 2. Using wave transformation
Taking into account Eq. (12), we reduce the FPDE to a nonlinear ordinary differential equation:
where U ’(ξ) = dU(ξ)/dξ.
P is a polynomial of U and its derivatives while u ξ = du/dξ, u ξξ = d 2 u/dξ 2 and so on.
Step 3. We introduce a functional variable for making a new transformation to unknown function U
and some successive derivatives of u(ξ) to following:
Step 4. After substituting (14) and (15) into (13) the ODE can be reduced as
After integration, Eq. (16) provides the expression of F, and this gives the appropriate solutions to the original problem, together with Eq. (14).
3.2. First integral method (FIM)
A summary of the FIM is presented,
Step 1. FPDE can be written in the form:
Step 2. Using wave transformation
Taking into account Eq. (19), we reduce the FPDE to a nonlinear ordinary differential equation:
where U ’() = dU(ξ)/dξ.
Step 3. Afterwards, defining some new independent variables
then we get a new system of the following form:
Step 4. By using the division theorem, we can reach a first integral to Eq. (22). The exact solutions of Eq. (17) are obtained by solving this equation.
Division Theorem: Suppose that R(x,y) and Q(x,y) are polynomials in C[x,y]; and R(x,y) is irreducible in C[x,y]. If Q(x,y) vanishes at all zero points of R(x,y), then there exists a polynomial H(x,y) in C[x,y] such that
4. Solution of the space-time fractional Phi-4 equation
The conformable space-time fractional Phi-4 equation [31]:
Using the following transformation:
where ξ is the transformation variable and l,λ be the constants. Eq. (23) changes into the form an ordinary differential equation:
4.1. Solution by functional variable method
Equation (25) can be written as follows:
Then we use the transformation u ξξ = (1/2)(F 2)’ in in Eq. (15), we get Eq. (27) from Eq. (26)
Integrating (27) with respect to u and we obtain
From (14) and (28), we deduce that
where ξ 0 is a integration constant. After integrating (29), we have the following exact solutions:
Case 1. If 2m 2 /n > 0 ⇒ m = 0, then
Case 2. If 2m 2 /n > 0 ⇒ m = 0, then
Case 3. If 2m 2 < 0, then
4.2. Solution by first integral method
Using Eq. (21) and Eq. (22), we can write two dimensional autonomous system
According to the first integral method, we suppose that X and Y are non-trivial solutions of the Eq. (39). Also,
where a m (X) 6= 0 and i = 0,1,...,m. By division theorem ∃ a polyn. g(X) + h(X)Y , such that
Assume that m = 1 then coefficients of Y i(i = 0,1) in Eq. (40), we have:
Since a i (X) are polynomials, then we deduce that a 1(X) is constant and h(X) = 0. Let us take a 1(X) = 1 and for the equilibrium of a 0(X) and g(X) degrees, deg(g(X)) = 1. Suppose that g(X) = A 0 + A 1 X and we find
where C is the integration constant. We obtain a nonlinear system of the algebraic equations from a 0(X), g(X), and Eq. (44).
And
Under the conditions given by Eqs. (46) and (47) in Eq. (40), we have,
Using Eq. (48) and Eq. (11), we can convert to Eq. (48) following Ricatti equation
Some special solutions are achieved:
Type 1. If 1/(l 2−λ 2) > 0, then
Type 2. If 1/(l 2 − λ 2) < 0, then
5. Graphical representations
5.1. Graphs of solutions with FVM
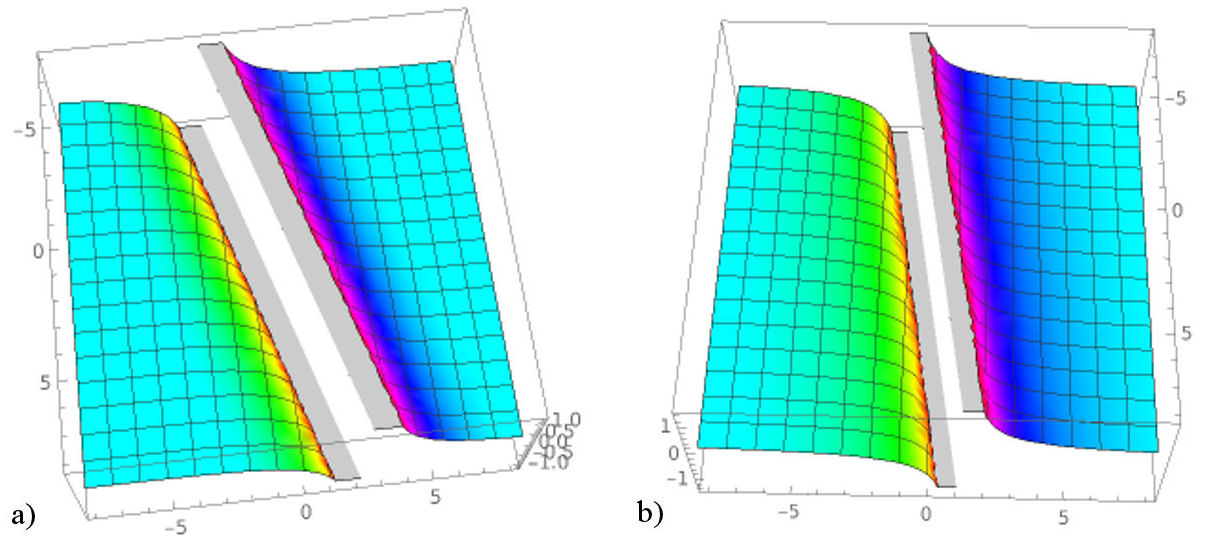
FIGURE 2 a) Graph of u 2 for m = −0.6, n = 1.06, λ = −0.2 and l = −0.7. b) Graph of u 2 for m = −0.2, n = 1.7, λ = −0.1 and l = −0.7.
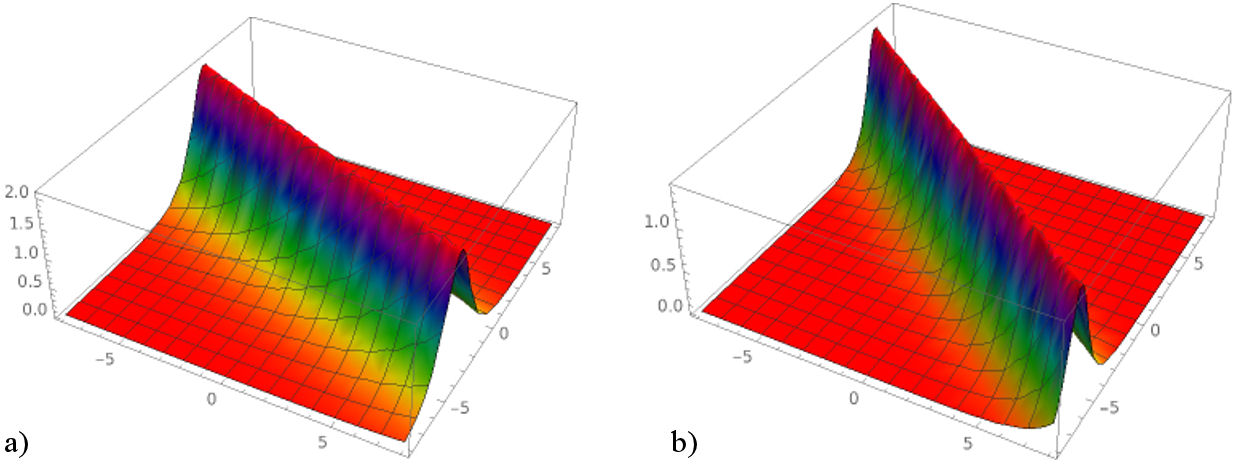
FIGURE 3 a) Graph of u 4 for m = −0.8, n = 0.3, λ = −0.4 and l = 0.9. b) Graph of u 4 for m = −0.8, n = 0.6, λ = −1 and l = 1.3.
5.2. Graphs of solutions with FIM
In this section, 3D graphs of the solutions have been included. Some specific parameters have been chosen to reach different types of wave graphs. Figures 2, 3, and 4 can give an opinion about the physical behavior of solutions based on the change of amplitude and width of the waves. While periodic solutions, hyperbolic solutions and rational solutions have been achieved by using FVM (Figs. 1-4), hyperbolic solutions, and trigonometric solutions have been obtained by using FIM (Figs. 5-8). The first method gives compacton waves and bell-shaped soliton waves whereas the second one gives compacton waves and kink soliton waves. Thanks to these powerful methods, different types of solutions can be helpful to understand the physical behavior of other nonlinear FPDEs in mathematical and nuclear physics.
6. Conclusions
In this paper, two powerful and reliable analytical techniques have been applied to Atangana’s conformable space-time fractional Phi-4 equation. Tha main advantage of FVM is its wide applicability. The main idea of FIM is reducing fractional partial differential equation to ordinary differential equation and then generating the first integral with the help of division theorem. The idea shows that the FIM is concisely direct. Thanks to FVM and FIM, we have obtained more solution functions than the other famous analytical methods. All solution functions have been checked by using the Mathematica program. Additionally, physical behaviors of solution functions have been examined for some appropriate values of the parameters. Results show that the proposed methods are very effective, straightforward, and strong to solve nonlinear FPDEs defined by Atangana’s derivative.











 nueva página del texto (beta)
nueva página del texto (beta)








