1. Introduction
Studies on entangled states have increased over the past years owing to further development of quantum mechanics [1-5]. Although Einstein and Schrödinger discovered entanglement in 1935 [6,7], some of its properties remain as a mystery. Schrödinger proposed his famous thought experiment where a cat is in a superposition the two distinct states ”alive” and “dead”. The life of the cat is uncertain until a measurement determines its destiny. Entanglement is the special state of two Schrödinger cats in quantum superposition. In the same year, Niels Bohr published an article [8] with the same title as the Einstein-Podolsky-Rosen article. Entanglement is a property of correlations between two or more quantum systems. These correlations defy classical description and are associated with intrinsically quantum phenomena. Researchers have made considerable contributions to quantum communication that have produced several approaches to allocating bipartite entanglement [4-9]. Entanglement of qutrit states [9] is attested by a quantum structure for the lower order terms of the density matrix. It is characterized by quantum dynamics of a three-level trapped ion using the quantum entropy of the system with a time-dependent Rabi frequency [10]. This entanglement is addressed with quantum correlations in negativity (N) and concurrence (C) [9,10] concerning the reduced and the total density matrices. Quantum discord is an optimal source for the difference between total correlation and classical correlation in a bipartite system [7,11] .
In nonclassical state generation in trapped ions, an external classical driving field is used to manipulate the coupling of internal electronic levels of the ion with its phonons. Physical models of such ion-phonon systems contain exponential nonlinearities in the motional degrees of freedom. However, these properties of entanglement result from the assumed linearity in the Lamb-Dicke limit (LDL). Beyond the LDL, the coupling between the internal and the external degrees of freedom becomes nonlinear. Studying the persistence of such effects beyond the LDL requires going beyond the linear assumption. A further rotating-wave approximation (RWA) yields the two-level quantum optical Hamiltonian governing phonon dynamics.
The GP has drawn considerable attention as a worthwhile means of attaining different phenomena in the processing of fault-tolerance in quantum information. In this sense, many scientists investigated some applications of this phenomenon [12-14]. First, we can review the outcomes as a modulation during the stage introduced by Berry [15]. It is shown that the Berry’s phase might be modified by weakly dissipative ”Liouville equation for the density matrix” through presenting imaginary correction [16] or damping the density matrix elements [17]. Recently, the influence of time-dependent coupling on the evolution of GP via the atomic speed and acceleration has been examined [18]. It is shown that the dynamic behavior of the GP and the entanglement of a threelevel atom with two fields in presence of the RWA include a richer structure than the absence of the RWA [19]. AbdelKhalek et al. [20] studied the impact of the cavity damping on the features of the GP and the entanglement of the three-level atom and field.
Trapped ions represent the most interesting applications of quantum bits (qubits) in processing quantum information because of long coherence times [21]. Ions restricted to a linear radio-frequency (Paul) trap are cooled with a spatial array. The Hilbert space of the composite quantum system takes the form
where d ion = 3 and d phonon = 4 are the dimensions of the three-level ion and photons, respectively. It is shown that the quantum dynamics with C [22], N [23], and quantum entropy [10] for a trapped three-level ion that interacts with two photons in time-dependent Hamiltonians. N and C are two measure of entanglement, which is a valuable representation in quantum information, especially in the ionic system. Entangled base and product base can be presented as a generalization of Schmidt coefficients. [24] show that the vibronic motion of a trapped ion far from the Lamb-Dicke regime (LDR) can be defined. It is shown that the full information on the quantum state of the vibrational center-of-mass (c.m.) motion of a trapped ion can be transferred to its electronic dynamics by long-living electronic transition by laser light [25].
A configuration for generating even and odd coherent states of the motion of a trapped ion is proposed with respect to laser excitation of two vibronic transitions [26]. Qubits are robust against noise
The outline of this paper is as follows. Section 2 presents the theoretical model and its solution under a classical field. The evolution of a qubit pure state from an initially unentangled state is described in Sec. 3. Section 4 investigates the temporal behavior of the GP and the population probabilities. Section 5 quantifies the entanglement according to the concurrence and the fidelity of the proposed system. Our main findings are summarized in Sec. 6.
2. Theoretical model and its solution under the classical field
A trapped three-level ion interacting with two laser beams in Λ configuration is proposed. In
this quantum system, the dimension of Hilbert space is 12. The quantum dynamics of
the trapped ion-phonon system has been previously investigated [8-10,33]. Additionally, the status of an ion-phonon system is
also valid for superposition of macroscopic quantum states with coupling of two
laser beams [34]. Trapped ions are
considered one of the best candidates to perform quantum information. Many of the
Ion-laser interactions cover the complete solutions [35]. The probability amplitudes of atomic levels of ion
are given:
The Λ scheme, namely a quantum scheme, in our model system is characterized by the total Hamiltonian Ĥ = Ĥ ion+ Ĥ 1 +Ĥ 2 +Ĥ c. The trapped ion Hamiltonian Ĥ ion and interaction Hamiltonians H 1 and H 2 are given as (ℏ = 1)
where mass of trapped ion is m, the harmonic trap frequency is ν in H
ion. The c.m. motion of the trapped ion can be described using the standard harmonic oscillator quantization of H
ion. This quantization includes the momentum and position operators
The matrix Ŝ rg is the r-g interaction of the classical field [37], and Ŝ gr the vice versa interaction. The last term Ĥ c represents the classical field, which has coefficient ε. Equation (2) includes the raman level energy ω r , the ground level energy ω g and the excited level energy ω e . The frequencies of the two laser beams are supposed to be equal ω = ω 1 = ω 2 and the Rabi frequencies of the dipole interactions between the lasers and the trapped ion are given by Ω. Thus, equality of Rabi frequencies such as Ω = Ω1 = Ω2 is given by the interaction Hamiltonians, in H 1 and H 2.
The relation between the Rabi and the harmonic trap frequencies is in the form of Ω/2 = ν in ion-phonon system.
The transition Rabi frequencies Ω e −g and Ω e −r are assumed to be equal and represented by
with tan(2β) = arctan(2ε/ω
g
− ω
r
). Here, β is the classical field effect.
Glauber displacement operators are given as D(±η) =
here
Two studies on ion-laser interaction help us understand photon dynamics [35,38]. The Hamiltonian of our model system is
The transformation is performed with the matrix
where,
where K(t) represents the eminent propagator for the cascade Hamiltonian [34], and e −itH̃0 is the rotating frame transformation representing the interaction. This shows the original state of our system, where the lower-order subsystem is in a coherent state. Under such settings, we obtain a robust entangled state in Figs. 1-4.
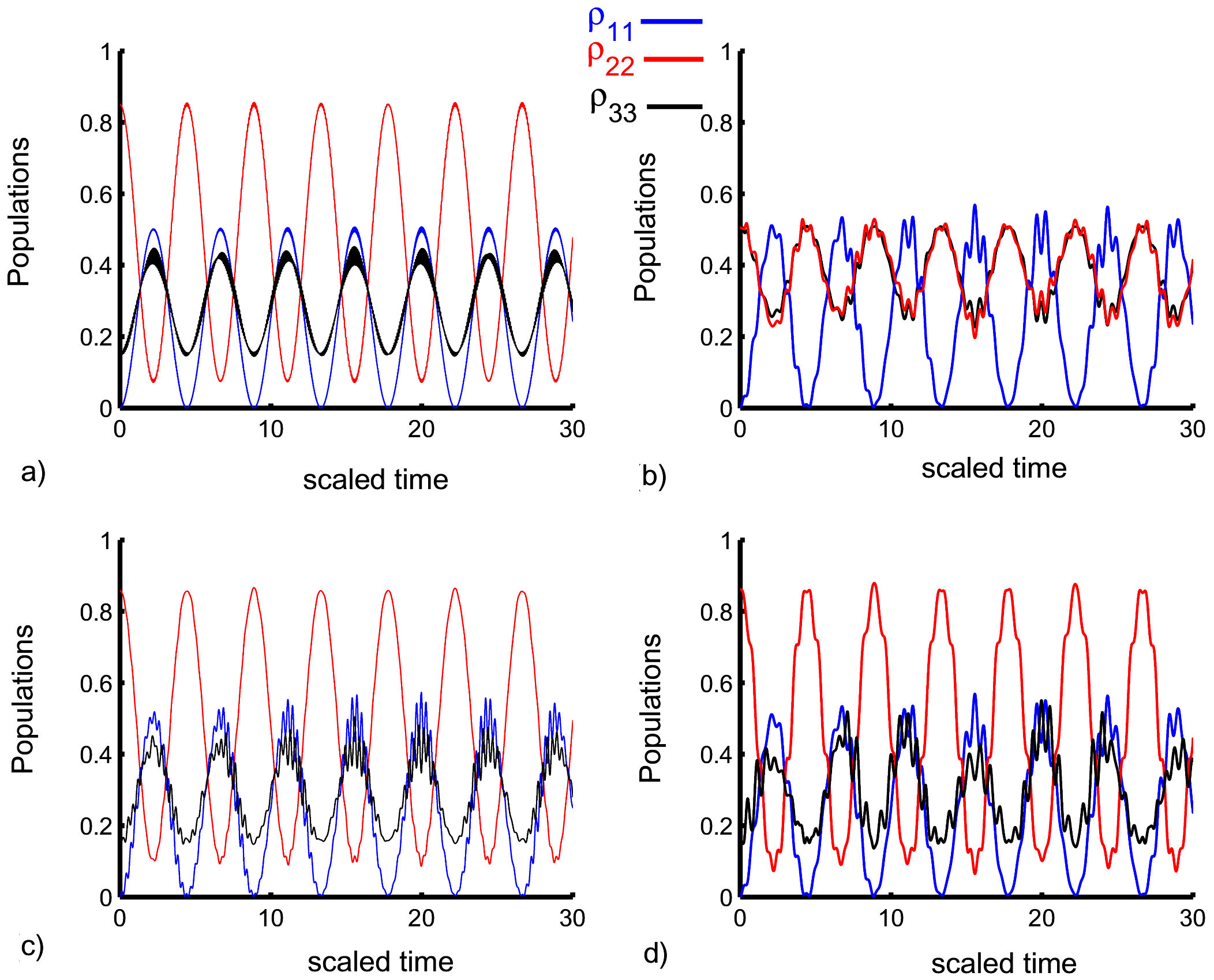
FIGURE 1 Population probabilities ρ 11(blue curve), ρ 22(red curve), and ρ 33 (black curve) versus scaled time for α = 0.05 with the two LDPs η =0.01 (a,c) and η = 0.1 (b,d) using the Planck constant equal to one, ℏ = 1. The classical field is ignored (i.e. β = 0) in (a,c) and considered for β = 0.49 in (b, d). The variable t is dimensionless time scaled with νη. The other coupling parameters are ω eg = 5×1014 Hz and ν = 1 MHz.
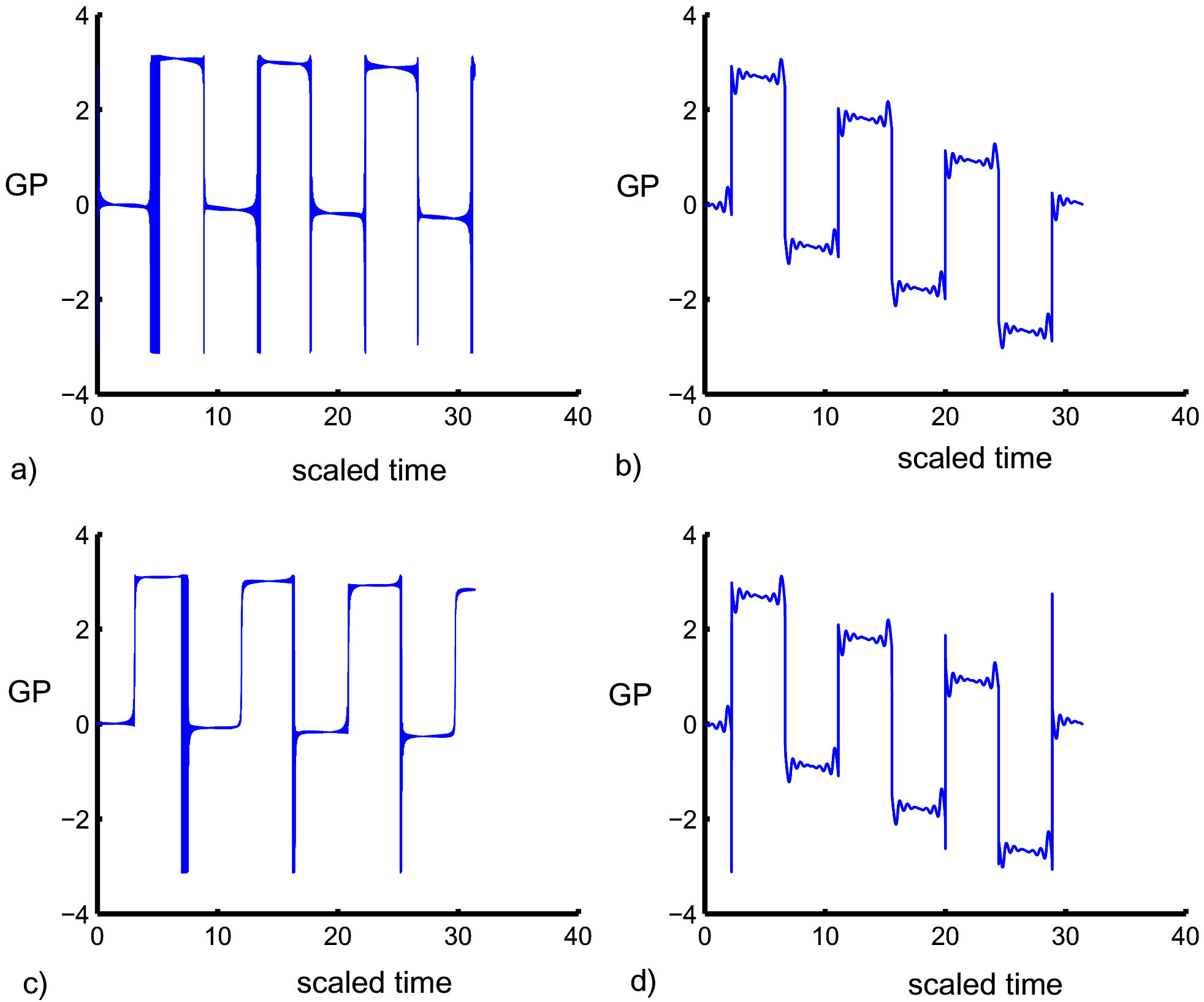
FIGURE 2 GP versus scaled time for α = 0.05 with the two LDPs η = 0.01 (a,c) and η =0.1 (b,d) using the Planck constant equal to one, ℏ = 1. The classical field is ignored (i.e. β = 0) in (a,c) and considered for β = 0.49 in (b,d). The other coupling parameters are the same as Fig. 1.
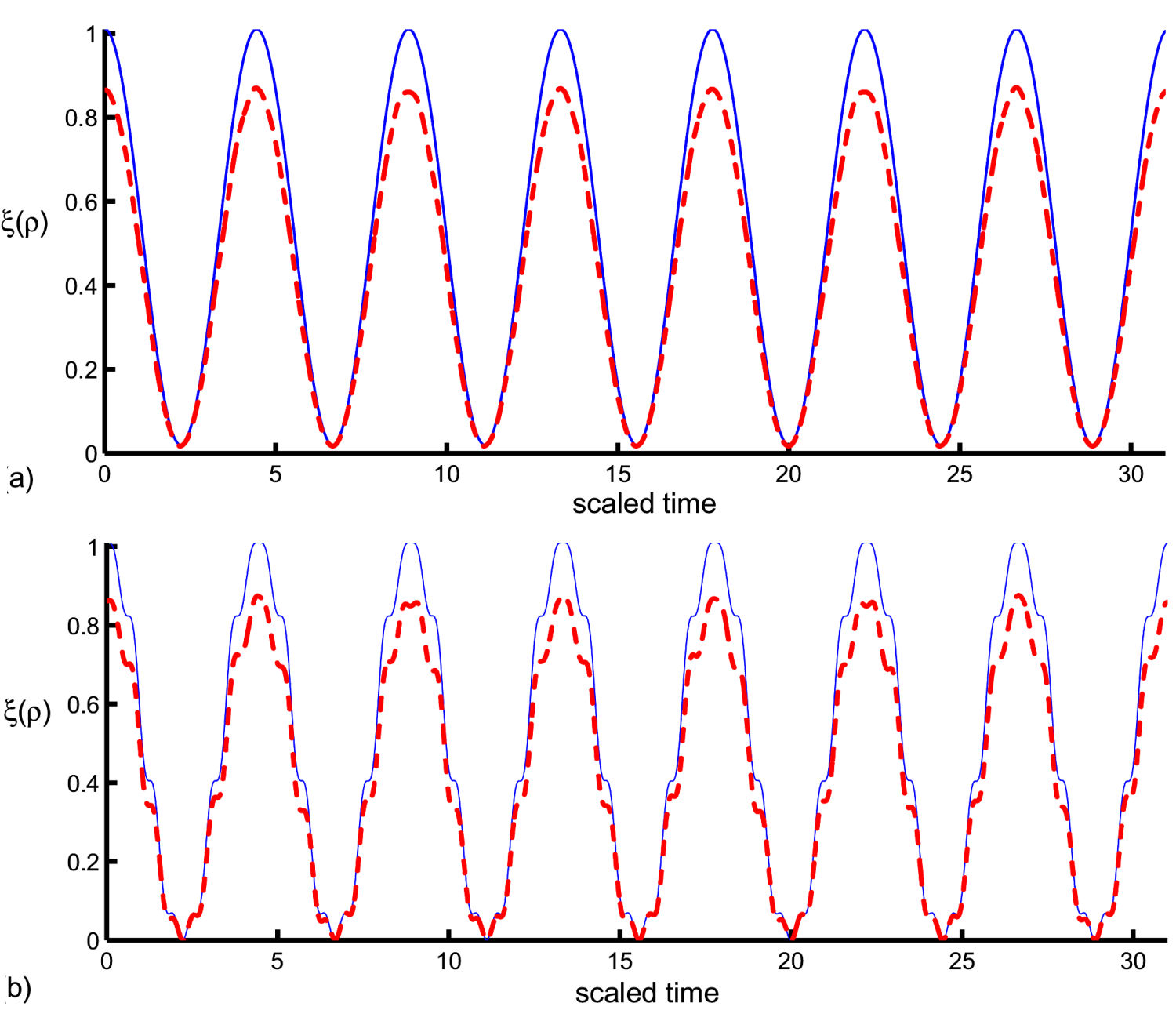
FIGURE 3 Fidelity ξ(ρ) versus scaled time for α = 0.05. The classical field is ignored (i.e. β = 0) along the (blue curve) and considered for β = 0.49 along the (dashed red curve). The two LDP values are η = 0.01 a) and η = 0.1 b). The other coupling parameters are the same as Fig. 1.
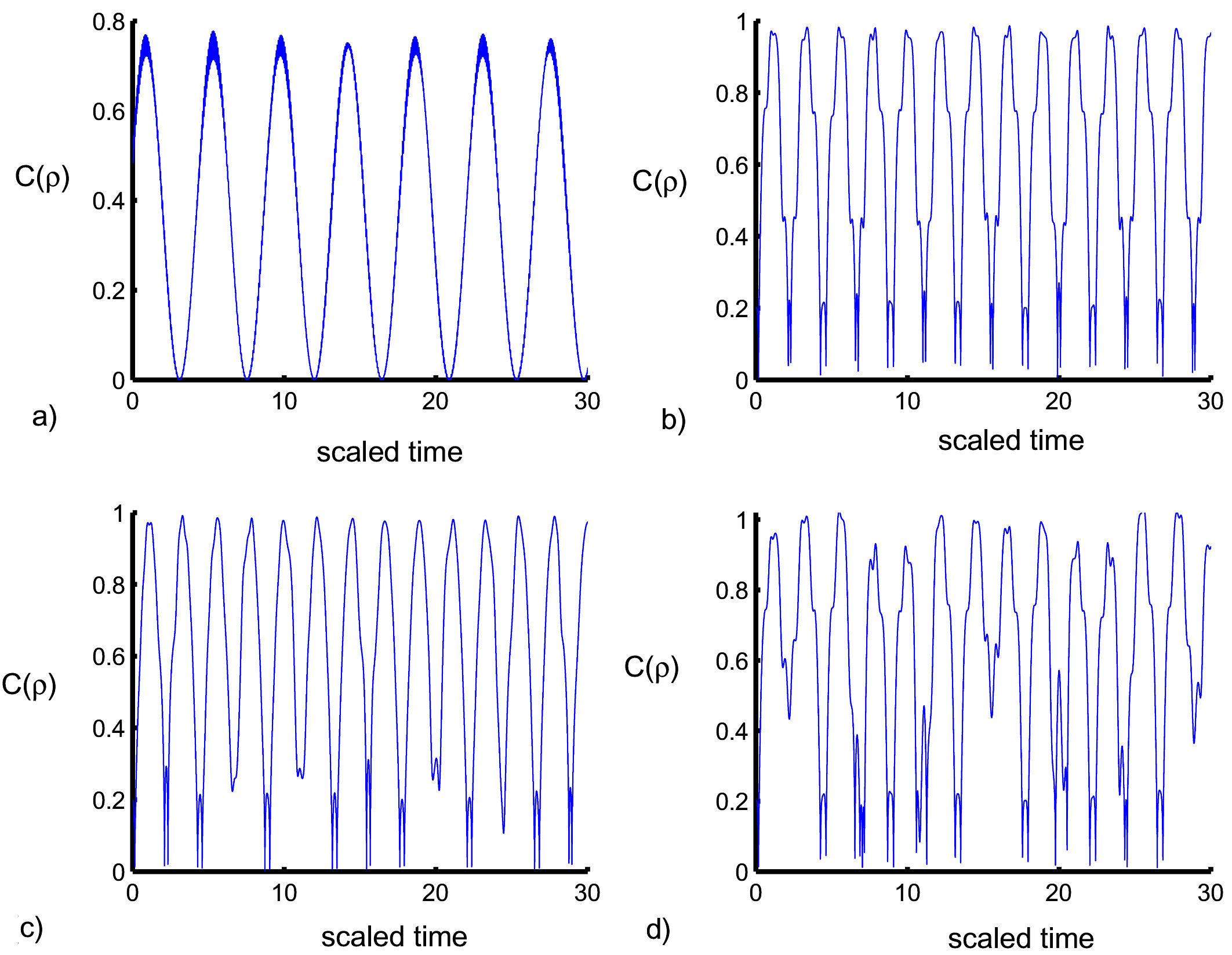
FIGURE 4 Concurrence versus scaled time for α = 0.05, with LDPs η = 0.01 (a,c) and η = 0.1 (b,d). The classical field is ignored (i.e. β = 0) in (a,b) and considered for β = 0.49 in (c,d). The other coupling parameters are the same as Fig. 1.
3. Evolution of a qubit pure state from an initially unentangled state
In the initial state of the ion-phonons system, the phonon subsystem is in a coherent state and the trapped ion is in the superposition state of its ground and raman levels that is
In optimal conditions, only a small mean photon number is required for producing entanglement.
This composite state is transformed into an initial case of the cascade
where t is dimensionless time scaled with νη (harmonic trap frequency-the LDP). In Figs. 1-4, a scaled time of 5 is equal to 500 microseconds for LDP=0.01. The calculation is as follows: If η = 0,01 and ν = 1 × 106 Hz, then νη = 104, (5/νη) = 500 × 10−6 = 500 microseconds. With the back unitary transformation U from the Ξ scheme to the Λ scheme, the wave function in the original space (e,r,g) takes the form
According to Eq. (3) and Eq. (4), the state vector of the system is precise in the infinite-dimensional Hilbert space. The situation of the system [34] is much more complicated than our system in the limited Hilbert space. The measurement of entanglement is very hard to comprehend owing to the complex construction of the system and the infinite-dimensional Hilbert space. The exact system is unclear in this case. Thus, we limit the Hilbert space so that the quantum state can be easily examined through Eq. (8). This equation eliminates the difficulties encountered in quantum measurements. The noteworthy coefficients becomes;
where ω = ω eg − η 2 ν and ω eg = ω 13 = 5 × 1014 Hz is the resonance frequency of the g − e transition.
4. Theoretical framework of population probabilities and the GP
The atomic population is very important in studying the entanglement between the parts of the system. In this section, we study the effects of both the classical field and the LDP on the atomic population.
First, we neglect the classical field (β = 0) and take the smallest value of the LDP (η = 0.01). It is clear that ρ
11(t) oscillates periodically between 0 and 0.5, while both ρ
22(t) and ρ
33(t) fluctuate identically between 0.25 and 0.5 as shown in Fig. 1a). The maximum values of the function ρ
22(t) increases strongly and reaches 0.83, but the amplitude of the oscillations decreases with respect to ρ
33(t) after the classical field is added (β = 0.49). The quantity ρ
11(t) is not affected as expected (the classical field rotates between ρ
22(t) and ρ
33(t)), as shown in Fig. 1(b). The fluctuations increase with the parameter η. The atomic population has the same behavior as in the previous case with an increasing maximum value under the classical field, as evident in Figs. 1c) and 1d). Here ρ
11 is the first diagonal term
where κ indicates a real scalar. GP is the phase achieved over the evolution of a state from
The classical field is initially excluded, and the LDP is at its smallest value (η = 0.01). The GP oscillates harmonically between −π and π with a period of 3π, as shown in Fig. 2a). These oscillations have rectangular form in the middle of the period, precisely at (3π/2). The rectangular oscillations in the previous case are shifted to the end of the period, precisely at (3π), after adding the classical field is added in to the interaction cavity (β = 0.49). The negative values of the GP function are reduced, as seen in Fig. 2b). Considering the large value of the LDP (η = 0.1) and the exclusion of the classical field, the GP has more oscillations and the fluctuations are still vertical between −π and π, as shown in Fig. 2c). The oscillations are reduced after the classical field is taken into account, as shown in Fig. 2d).
5. Entanglement measures and fidelity
In the quantum information scheme, fidelity is used to evaluate the transformation between the changing and fixed states.
In this part, we study fidelity defined as [41,42]
where |ψ(t)i is given by Eq. (7).
For the minimum LDP value (η = 0.01), the fidelity fluctuates smoothly between 0 and 1 every π without the classical field. This indicates weak entanglement between the two phonons and the trapped ion. The function ξ(t) decreases after the classical field is added to the interaction cavity, as shown in Fig. 3a). Previous oscillations are decreased slightly after the LDP is increased (η = 0.01 → 0.1), so the parameter is influenced by the entanglement of the system parts. Comparing the previous results, we notice that the classic field reduces the entanglement in ion-phonon system, as shown in Fig. 3b).
The total density operator ρ
ion−phonon is represented by a 12×12 D matrix in the base of
where the diagonal terms,
where
An arbitrary bipartite pure state is written as [43-45]
where ρion = Tr phonon(ρion−phonon) is the reduced density operator. We are currently discussing concurrence through the same aforementioned conditions. For the smallest values of the LDP (η = 0.01) without the classical field, the concurrence C(t) oscillates regularly between 0 and 1 and reaches the minimum values periodically, as shown in Fig. 4a). The oscillations of the function C(t) increase and decrease to the smallest values after the increase in η.
In addition, the maximum values are raised to the top by increasing η as shown in Fig. 4c). For the small values of the η, the high values of the function C(t) rise sharply. Furthermore, some lower values decrease after the addition of the classical field to the interaction cavity as see in Fig. 4c). While the maximum values that is the peaks decrease, the minimum increases after the parameter η increases. Therefore, entanglement is greatly influenced by the parameter η of the classical field as shown in Fig. 4d).
Consequently, the optimum values in our figures agree with the results of other studies, that deal with elaborated quantum measurements such as fidelity and C [7,46-51]. This is because, in an ion-phonon system, the amount and duration of entanglement are developed in comparison with other studies.
6. Conclusion
We considered the interaction between a three-level trapped ion with two laser beams in a Λ (lambda) configuration. The general solution for the present system was obtained with a wave function. Using this wave function in 12-D space, we obtained an analytic solution of the total density operator, ρ ion−phonon = U †(t)[ρ i(0) ⊗ ρ p(0]U(t). The resulting population and GP were considered in the presence and absence of a classical field. It turns out that the classical field strongly affects the population and the geometric phase. We used four different variations of these two factors, the LDP and the classical field. We observed that the physical and dynamical properties of the quantum quantifiers can be controlled by appropriately selecting the classical field and the LDP. In population inversion, the amplitude of the oscillations decreases in the presence of the classical field. The oscillations improve as the LDP increases. In the GP, the negative portions decrease after the classical field is included in the interaction cavity.
When the classical field comes from 0 to 0.49, fidelity and C values rise in Figs. 3-4. We can say that fidelity and C are two measures elaborated for entangled qudit states. The phenomenon of sudden death and sudden birth decreases with increasing LDP and the classical field. The entanglement fluctuates regularly with increasing LDP and reaches a state of separation periodically. This insight may have useful applications in quantum optics and information processing.











 nueva página del texto (beta)
nueva página del texto (beta)


