1. Introduction
The search for clean and renewable energy is currently an urgent challenge globally.
The utilization of waste heat has been gaining increasing attention with the
increasingly serious problems of fossil energy depletion and environmental
pollution. Thermoelectric materials have attracted increasing attention because they
can harvest waste heat and convert it directly into electricity, given their
promising performances in energy conversion applications. The conversion efficiency
is measured by the dimensionless figure of merit
Research on Heusler alloys, Half Heusler (HH) and Full Heusler (FH), having,
respectively, a general formula XYZ and X2YZ (X/Y are transition metals,
Z = p-block elements) have constantly drawn the attention of the researchers due to
their remarkable various applications, such as Half metals 1, ferromagnetic shape memory alloys 2, superconductivity 3, and spintronics 4. Also, as for compounds HH
compounds, the Full Heusler (FH) materials have thus attracted attention as
thermoelectric (TE) materials 5-9. Although very high PFs at room temperature have been
reported in FH compounds based on Fe2VAl 10-12, the effective ZT values are merely around 0.13-0.2 at
300 K due to the high thermal conductivity (intrinsic κL = 28 W
Nevertheless, the search for novel, highly efficient, and cost-effective materials is an open challenge to researchers; and in contrast to conventional FH compounds, there are a new class of stable semiconducting FH compounds with intrinsically high PFs and extremely low lattice thermal conductivity due to atomic rattling, which we call R. Heusler (Rattling Heusler) compounds. These compounds, which to our knowledge have very little been reported in the literature, contain ten valence electrons per f.u. 14-16. In order to enlarge studies in this new field of material, we investigate in this paper the structural, electronic, thermodynamic, and thermoelectric properties of the three new Rattling Heuslers Ba2AgZ (Z = As, Sb, Bi) with alkaline earth elements Ba in the X sublattice, whereas Ag is a noble metal and Z is As, Sb and Bi elements. It is expected that this paper will open new avenues for especially thermoelectric applications. The remainder of the article is organized as follows: The technical details of calculations have been reported in Sec. 2. The details of crystal structure and the main results for the structural, electronic, thermodynamic, and thermoelectric properties are presented in Sec. 3. A brief conclusion of the results is finally given in Sec.4.
2.Method of calculations
We have carried out first the principles calculations 17,18 with both Full potential and linear augmented plane wave (FP-LAPW) methods 19 as implemented in the WIEN2k code 20. The exchange-correlation effects were described with the parameterization of the generalized gradient approximation (GGA) 21. Well-converged basis sets are chosen with RMT Kmax = 8 while Gmax =12Ry1/2 for the Fourier charge density expansion of the potential in the interstitial region is used. A mesh of 104 special k-points was made in the irreducible wedge of the Brillouin zone. An energy threshold of - 6 Ry is used to separate the valance and core states for all calculations.
3.Results and discussions
3.1.Structural properties
As is known, the so-called Full Heusler alloys crystallize in a highly ordered
cubic structure, and their properties are related to the site preference of the
atoms inside the structure. There are two types of highly ordered atomic
arrangements 22:
AlCu2Mn (space group 225 F -m3m) and CuHg2Ti-type
structures (space group 216 F-43m). For Ba2AgZ (Z = As, Sb, Bi)
alloys in the AlCu2Mn-type structure, the atomic sites are described
as follows in Wyckoff coordinates: Ba (0,0,0), Ba (0.5,0.5,0.5), Ag
(0.25,0.25,0.25), and Z (0.75,0.75,0.75), and in the CuHg2Ti-type
structure, they are Ba (0,0,0), Ba (0.25,0.25,0.25), Ag (0.5,0.5,0.5), and Z
(0.75,0.75,0.75). Structural optimizations on the Ba2AgZ (Z = As, Sb,
Bi) alloys were performed first to determine their equilibrium lattice
constants. The total energy-lattice constant curves for these alloys are plotted
in Fig.1. Clearly, the
AlCu2Mn-type structure state is energetically the most stable
structure in comparison to the Hg2CuTi-type at the equilibrium
lattice constant for these three alloys. The values of the optimized parameters
are given in Table I and are 8.06, 8.35,
and 8.46 A for Ba2AgAs, Ba2AgSb and Ba2AgBi,
respectively. The equilibrium lattice constant of these alloys increases with
the increasing covalent radii of the Z atoms (i.e., As→Sb→Bi). The formation
energy E
f
determines whether a compound can be experimentally synthesized or not
23. E
f
is the change in energy when a material is formed from its constituent
elements in its bulk states and can be calculated for Ba2AgZ (Z = As,
Sb, Bi) compounds as

Figure 1 Total energy as a function of unit cell volume for the Ba2AgZ (Z = As, Sb, Bi) compounds in both Cu2MnAl and Hg2CuTi type structure.
Table I Calculated total energies Etot (in Ry) per formula unit, equilibrium lattice constant a0 (in Å), the bulk modulus B (in GPa), the formation energy (in Ry) and the energy gap Eg (L − ∆)(in eV) for Ba2AgZ (Z= As, Sb, Bi) compounds in theirs different structures type configurations
| Compound | structure | E tot | a0 | B0 | E f | Eg (L − ∆) |
| Ba2AgAs | Cu2MnAl | -47714.477781 | 8.065 | 32.43 | -0.84 | 0.566 |
| Hg2CuTi | -47714.329083 | 7.890 | 30.77 | -0.56 | ||
| Ba2AgSb | Cu2MnAl | -56159.551580 | 8.353 | 28.24 | -0.748 | 0.548 |
| Hg2CuTi | -56159.413848 | 8.143 | 26.38 | -0.535 | ||
| Ba2AgBi | Cu2MnAl | -86355.348178 | 8.460 | 25.62 | -0.52 | 0.433 |
| Hg2CuTi | -86355.223962 | 8.273 | 24.09 | -0.19 | ||
| Ba2AuSb[15]FP-LAPW | Cu2MnAl | 8.28 | 32 | 0.72 | ||
| Ba2AuBi[15]FP-LAPW | Cu2MnAl | 8.37 | 30 | 0.57 |
3.2.Electronic properties
It is well known that the band structure is vital for determining the thermoelectric properties because these properties depend greatly on the band structure. The calculated band structures of Ba2AgZ (Z = As, Sb, Bi) R compounds have been illustrated in (2-4)a. As it can be seen, the general band structures of are similar for our R FH compounds. The valence band maximum (VBM) and conduction band minimum (CBM) are located at the low symmetry points L and Δ (between Γ and X) in the Brillouin zone indicate that Ba2AgZ (Z = As, Sb, Bi) alloys are indirect bandgap semiconductors. The indirect energy gap Eg (L - Δ) of 0.566 eV for Ba2AgAs, 0.548 eV Ba2AgSb and 0.433 eV for Ba2AgBi is obtained. Unfortunately, so far, no experimental measurements and theoretical data bandgap Eg for the investigated compounds are carried out to compare with. However, our results for bandgap Eg listed in Table I are in good agreement with the other theoretically work for the same family of rattling Full Heusler Ba2AuZ (Z = Sb, Bi) 15.
Furthermore, multiple bands have energies close to the VBM and CBM and lead to a
sharp increase in the density of states around the Fermi level, which is
favorable for large Seebeck coefficients. Bilc et al. 13 recently showed that bands that are flat
along one direction and highly dispersive along others lead to a high Power
factor (PF) in FH materials. In fact, such bands are present in ours new R
compounds Ba2AgZ (Z = As, Sb, Bi) as well, where the valence band
along
Table II Calculated elastic constants C ij (in GPa), Bulk modulus B (in GPa), Poisson’s ratio v, anisotropy factor A and B/G ratio for Ba2AgZ (Z = As, Sb, Bi) compounds
| Compound | C11 | C12 | C44 | B | v | A | B/G |
| Ba2AgAs | 59.96 | 18.86 | 15.64 | 32.56 | 0.27 | 0.76 | 1.87 |
| Ba2AgSb | 55.67 | 14.33 | 7.97 | 28.11 | 0.33 | 0.38 | 2.38 |
| Ba2AgBi | 57.12 | 11.72 | 17.80 | 26.85 | 0.21 | 0.78 | 1.37 |
Table III Calculated values of heat capacity C V (in J·mol −1·K −1), entropy S (J·mol −1·K −1) and Debye temperature θ D (in K) at 300 K for Ba2AgZ (Z= As, Sb, Bi) compounds.
| Compound | C v | S | θ D |
| Ba2AgAs | 98.08 | 185.35 | 175.55 |
| Ba2AgSb | 98.35 | 195.68 | 161.26 |
| Ba2AgBi | 98.56 | 203.73 | 148.61 |
| Ba2AuSb[15]FP-LAPW | 98.362 | 196.214 | 160.39 |
| Ba2AuSb[15] FP-LAPW | 98.644 | 207.3 | 143.32 |
We observe that above the Fermi level, the conduction band is heavily dominated by Ba-4d and (As-4p*, Sb-5p*, Bi-6p*) states for all R Heusler compounds, while below the Fermi level, in the top of the valence band represented by the three bands between 0 and -2 eV, TDOS is predominant by (As-4p, Sb-5p, Bi-6p) orbitals with a minor contribution from Ag-5𝑠 represented by the single valence band around -2.5 eV for Ba2Ag(As, Sb, Bi) compounds, respectively. The two most electropositive atoms Ba donate their four 5s electrons to the electronegative Ag and (As, Sb, Bi) atoms. Thus, the Fully occupied 4d (represented by the flat valence bands around -4.5 eV) and 5s states of the Ag atom are extremely localized and far below the Fermi level, such that Ag only weakly interacts with its neighboring atoms. Also, the As-4s, Sb-5s, and Bi-6𝑠 electron lone pairs are deep below the Fermi level and are chemically inactive, represented by the single valence band around -9 eV. Therefore, as it is presented in Figs. (2-4)c, although the R compounds have in total ten valence electrons per f.u., these latter inactive (As-4s, Sb-5s, and Bi-6s) lone pairs lead effectively to an eight-electron system, resulting in filled bonding and empty antibonding states following the electron counting rule to obtain a semiconductor.
3.3.Thermodynamic properties
Thermodynamic properties of materials are closely related to their volume;
therefore, examining the volume change under different working conditions of
temperature and pressure is very important to design materials. Thermodynamic
properties of the Ba2AgZ (Z = As, Sb, Bi) R compounds have been
determined using the GIBBS2 code, which is an implementation of the
quasi-harmonic Debye model 24,
in which the non-equilibrium Gibbs function
where E(v) is the total energy per unit cell, PV corresponds to the constant
hydrostatic pressure condition,
where n is the number of atoms per formula unit,
where M is the molecular mass per unit cell and Bs the adiabatic bulk modulus, approximated by the static compressibility 26:
where f(σ) is given by Ref. 26; σ is the Poisson ratio. Therefore, the non-equilibrium Gibbs function G * (V;P,T) as the function of (V; P,T) can be minimized with respect to volume V,
By solving Eq. (18), one can obtain the thermal equation of state (EOS) V(P,T). The heat capacity CV and the thermal expansion coefficient α are given by 27,
where
In this work, properties are calculated in a wide range of temperature and pressure, from 0 to 1000 K and from 0 to 20 GPa, respectively. Heat capacity CV is related to the lattice vibrations and internal energy, which are responsible for many physical properties of materials. The variation of Ba2AgZ (Z = As, Sb, Bi) heat capacity CV as a function of temperature at fixed pressures is displayed in Fig. 5a). It is important to mention that at temperature 0 K, the heat capacity always takes zero value, implying the absence of lattice vibrations in the material.
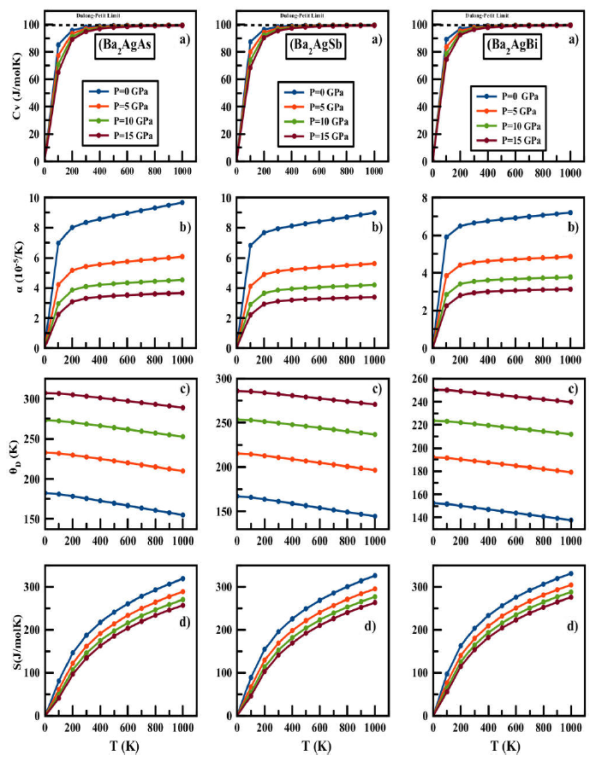
Figure 5 a) Heat capacity C V , b) thermal expansion coefficient α, c) Debye temperature θ D , and d) entropy S vs temperature and pressure for Ba2AgZ (Z = As, Sb, Bi) alloys calculated by quasiharmonic Debye approximation.
The CV, along with the temperature of all compounds, increases rapidly
up to 200 K. Beyond this temperature, the rising rate decreases considerably,
and the heat capacity tends to the saturation value, corresponding to the
Dulong-Petit limit, indicating the thermal excitation of all phonon modes in all
ours R compound. Results suggest that the lattice vibrations will become
stronger by increasing temperature, and a contrary behavior can be obtained when
raising pressure. A stronger dependence on temperature of the heat capacity is
obtained than on pressure. The predicted values of specific heat of
Ba2AgAs, Ba2AgSb, and Ba2AgBi alloys at 300
K and 0 GPa are 98.08, 98.35, and 98.56 J
Debye temperature is another thermodynamic parameter, which can be used to
characterize the strength of covalent bonds. High values of Debye temperature
also suggests the good hardness of the material, while low values are frequently
found in soft materials. Figure 5c) shows
the change of the Debye temperature under the effect of temperature (at several
constant pressures). From these plots, it is found that the
3.4.Thermoelectric properties
In order to estimate the thermoelectric performance of ours compounds, we have
computed the transport properties such as Seebeck coefficient S, thermopower
factor PF, electrical conductivity σ, electronic thermal conductivity
The transport coefficients σ , κ, S, ZT and PF as a function of temperature (T) and chemical potential (μ) are obtained from the following equations:
where Ω is the volume of the unit cell and f0 is the Fermi-Dirac
distribution function, and
The results are plotted in Fig 6(a-f). An
efficient thermoelectric material is required to have high electrical
conductivity, low thermal conductivity, and a large Seebeck coefficient. The
variation of the electrical conductivity

Figure 6 The variation of electrical conductivity σ / τ a), electronic thermal conductivity ·e, lattice thermal conductivity · κ L , total thermal conductivity · κ tot b)-d), Seebeck coefficient S e) and figure of merit ZT f) as a function of temperature for Ba2AgZ (Z = As, Sb, Bi) alloys.
Figures 6(b-d) displays the temperature
dependences of total thermal conductivity (
where
It is clear that the temperature dependence of the electronic thermal
conductivity κe is similar to the behavior of electrical
conductivity. The lattice thermal conductivity decreased as the temperature
increased in all materials because, at high temperatures, the phonon scattering
is dominated by Umklapp processes and may stand it as a potential candidate for
thermoelectrics. All ours R Heusler compound exhibit extremely low κL
of 0.275, 0.323 and 0.384 W.m-1
We have estimated the electrical conductivity as shown in Figs. 6a). As the temperature increases, an exponentially increasing trend can be seen, which may trigger its thermoelectric efficiency. This increasing conductivity is attributed to the semiconducting behavior of the alloys.
The variation of total thermal conductivity κ is shown in Figs. 6b)-d), where the electronic thermal conductivity κe increases with temperature, while the lattice part κL decreases with an increase in temperature. In the case of electronic thermal conductivity κe, as the temperature increases from 300 to 1000 K, the exponential increase occurs from 0.041, 0.0382, and 0.0373 W/mK to 0.825, 0.71, and 0.72 W/mK for Ba2AgAs, Ba2AgSb and Ba2AgBi, respectively. In the case of lattice thermal conductivity κL, there is a decrease from 0.83, 0.97 and 1.15 W/mK at 100 K to 0.0825, 0.097, and 0.16 W/m Kat 1000 K for Ba2AgAs, Ba2AgSb, and Ba2AgBi, respectively. These values are very small as compared to traditional Full Heusler alloys 6,10,13. The capability of showing lower lattice thermal conductivity may stand it as a potential candidate for thermoelectrics.
The total thermal conductivity κtot shows an exponential decaying trend in all compounds up to 400 K due to the abrupt increase of large phonon vibrations before increasing slightly with temperature. We also computed the total Seebeck coefficient S variation calculated to designate its nature as shown in 6e). As one can see, the Seebeck coefficient of our R. Heusler compound is positive. The positive sign of S explains that the holes are dominant charge carriers. Therefore, our R. Heusler compounds are p-type materials. The calculated transport coefficients are now used to estimate the thermoelectric efficiency through the figure of merit ZT measurement. The materials are considered as good elements for thermoelectric devices if their ZT is about or greater than unity 33. The variation of ZT is shown in 6f), which shows linearly that ZT increase with increasing temperature. At room temperature, these values are respectively 0.175, 0.143 and 0.121 for Ba2AgAs, Ba2AgSb and Ba2AgBi. At 1000 K, its respective maximum values are 0.76, 0.73 and 0.52 respectively. It is clear that a higher temperature results in a higher figure of merit for the compound Ba2AgAs with respect to Ba2AgSb and Ba2AgBi but Ba2AgAs is regarded as a promising thermoelectric material. The value of electrical conductivity, thermal conductivity, Seebeck coefficient, and figure of merit ZT at room temperature are summarized in and compared with other R. Heusler 14-16 and Full Heusler compounds 6,7,9.
Table IV Values of electrical conductivity σ / τ (in 1018
| Compound | σ / τ | κ L | κ tot | S | ZT |
| Ba2AgAs | 3.1 | 0.275 | 0.316 | 260 | 0.1 |
| Ba2AgSb | 3.2 | 0.323 | 0.361 | 244 | 0.143 |
| Ba2AgBi | 3.3 | 0.384 | 0.421 | 237 | 0.121 |
| Ba2AuSb[15] | 1106.23FP-LAPW | ||||
| Ba2AuBi | 0.5[14]PAWF | 848.30[15]FP-LAPW | |||
| Ba2HgPb[14] | 0.5[14]PAWF | ||||
| Sr2PtSe[16] | 7.9FP-LAPW | 21.7FP-LAPW | 2:08 x 10-3 FP-LAPW | ||
| Sr2PtTe[16] | 8.7FP-LAPW | 9.02FP-LAPW | 1:27 x 10-3 FP-LAPW | ||
| Li2ZnGe[6] | 2.37FP-LAPW | 2.65FP-LAPW | ∼-60FP-LAPW | 0.025 FP-LAPW | |
| Zr2NiAl[7] | 3.0206FP-LAPW | ∼-25FP-LAPW | ∼0.055 FP-LAPW | ||
| Zr2NiGa[7] | 2.1607FP-LAPW | ∼-17.5FP-LAPW | ∼0.01 FP-LAPW | ||
| Fe2VAl | 15[8]Exp | 16[8]Exp | ∼-20[8]Exp | ||
| 3.3[13]B1-WC | 28[10]Exp | ||||
| Ru2VAl[9] | ∼10Exp | ∼-12.5Exp | ∼0:35 x 10-3 Exp | ||
| Ru2VGa[9] | ∼13.5Exp | ∼8Exp | ∼0:6 x 10-3 Exp |
Table V Calculated thermoelectric power factors PF (
| Compound | p-type doping level | PF | n-type doping level | PF |
| Ba2AgAs | -0,45 | 15 | +0.35 | 6.1 |
| Ba2AgSb | -0.461 | 9.6 | +0.34 | 6.5 |
| Ba2AgBi | -0.422 | 9.2 | +0.265 | 6.8 |
| Ba2AuBi[14]PAWF | ∼-0.6 | 10 | ∼+0.4 | 6 |
| Sr2AuBi[14]PAWF | ∼-0.55 | ∼10.5 | ∼+0.375 | ∼15.5 |
| Fe2VAl[13]B1-WC | ∼-0.6 | ∼7 | ∼+0.45 | ∼3 |
Finally, the applicability of material for thermoelectric technology is reflected
in terms of power factor PF. The high power factor of material suggests high
efficiency. The variation of power factor PF at 300 K as a function of chemical
potentials (μ) are plotted in Fig. 7. The
compound is considered pure at the zero chemical potential (μ = 0 eV), which is
located at the middle of the bandgap. The positive value of μ represents the
n-type doping, while the negative μ describes the p-type doping. The optimal
doping level at which the power factor reaches the highest value is one of the
main aspects in the domain of thermoelectric compounds. From 7, it is clear that
the PF of hole-doping (p-doping) is larger than that of electron-doping
(n-doping); this signifies that p-type is better than n-type doping. Following
the work of Bilc et al., 13
and He et al. 14, a constant
relaxation time of
4.Conclusion
Based on the density functional theory, we have employed the FP-LAPW method with the GGA approximation to investigate the structural, electronic, thermodynamic, and thermoelectric properties of the new Ba-based Rattling Full Heusler alloys Ba2AgZ (Z = As, Sb, Bi). In all compounds, the stable AlCu2Mn-type structure was energetically more favorable than the Hg2CuTi-type structure. The calculated lattice constants and bulk modulus of the compounds are in good agreement with other theoretical data. From the study of the electronic properties, we predicted that these compounds have a semiconductor behavior with an indirect bandgap (L - Δ). The quasi-harmonic Debye model was used to determine the thermodynamic properties comprising the thermal expansion, heat capacity, entropy, and Debye temperature parameter in the pressure range of 0-15 GPa when the temperature varied from 0 to 1000 K. Boltzmann’s theory was employed to study the thermoelectric properties which include electrical conductivity, electronic thermal conductivity, lattice thermal conductivity, Seebeck coefficient and power factor. These materials exhibit high values of Seebeck coefficient, and power factor and low lattice thermal conductivity with room temperature due to flat-and-dispersive valence bands. These properties establish these novel Rattling Full Heusler compounds as very promising thermoelectric materials. To our knowledge, no other studies of thermoelectric are available in the literature for these materials; thus, it would be beneficial to verify experimentally our predicted results.











 nueva página del texto (beta)
nueva página del texto (beta)






