1.Introduction

Several methods as the Reverse Monte Carlo (RMC) and the Rietveld for Disordered Materials (RDM), have been applied to make a structural study of the BaMn(Fe/V)F₇ transition metal Fluoride glass, assuming isomorphous replacement. The results show that only the six (6) first F atom neighbours were constrained around Mn and Fe/V atoms. And the octahedra [MnF₆, (FeF₆/VF₆)] linkage is realized by corner and edge sharing into the BaMn(Fe/V)F₇ in crystallized compounds. The Barium atom is inserted into the interstice between MnF₆ octahedra ^1-5 as shown in Fig. 1.

Figure 1 The BaMn(Fe/V)F7 structure by the (RMC) simulation. (Fe,V)F6 polyhedra in blue, MnF₆ polyhedra in green, Ba atoms as yellow spheres ¹. 

In recent years, the structural properties of the BaMn(Fe/V)F₇ Fluoride glass have been studied by displaying the partial pair distribution functions (PDFs) g(r) between all species of the system using the RMC and the Hybrid Reverse Monte Carlo (HRMC) simulation techniques . The HRMC method is obtained by a modified simulation protocol based on the RMC algorithm, whose physical or chemical constraint is introduced based on the understanding of the material being modelled. In our last study, we introduced an energy penalty term (Buckingham potential) in the acceptance criteria to give it a move realistic feature, and to remedy the problem of the artificial satellite peaks, which appear in the PDFs in the RMC simulation ^5,6.

It is possible to model complex systems by potential pairs for many classes of liquids and to use simple fluid theory for the description of their structural and thermodynamic properties. Indeed the choice of the interatomic potential type, describing the interaction between the different constituents in the simulation, is fundamental for obtaining a reliable initial structure in which the glassy state will be prepared. In our case, the best results are obtained by the Buckingham potential.

Describing the thermodynamic properties of the glassy state of binary and multicomponent mixtures of molecular and ionic compounds is still poorly understood ^7,8. The phenomenological model of the vitreous transition for a glass has a single parameter of structural order, and since this parameter manifests extreme similarity between the liquid state and the glassy state, it shows that there is no important evolution of the structure of the glass transition. This confirms the hypothesis that the glass retains the structure presented by the liquid at the glass transition temperature T_g⁹.

This paper represents a modest attempt to provide information on the structure, and to predict thermodynamic properties of the BaMn(Fe/V)F₇ Fluoride glass by using the structural parameter g(r) derived from the application of the Buckingham potential in the RMC simulation (5).

2.Computational methods

A complete description of the HRMC method has been detailed in our previous papers ^4-6,10-14. We present here a brief summary. The RMC method ^15-17 is combined with the Metropolis Monte Carlo (MMC) method ¹⁸, in an attempt to minimize the agreement factor χ of an atomic system. The χ obtained from the atom positions in the system, represents a weighted difference between the calculated and the experimental system structural features for the RMC method and a temperature-weighted total energy, the form of which depends on the interatomic potential used, for the MMC method in the different ensembles (NVT), (μVT), and (NPT). The explicit form of χ for the G(r) is given by:

where σ(ri) is an estimate of the experimental error and ω is a weighting parameter.

Minimization of χ is carried out through random individual displacements of atoms, where the χ_old and χ_new calculated before and after each displacement, respectively, are compared. If χnew<χold, the move is accepted. If χnew>χold, the move is not rejected outright but accepted with a conditional probability

where χ_old is calculated using G(r)oldRMC and U_old, and χ_new using G(r)newRMC and U_new.

The energy of the system is calculated by using the Coulomb-Buckingham potential expressed by:

where q_i, q_j are the charges of the individual ions, ε0 is the permittivity of free space, A_ij is a parameter characterizing the depth of the potential well, and ρij is the slope of the short range exponential repulsion known as the hardness parameter ¹⁹. The Buckingham potential parameters are selected by fixing the hardness parameters for all the ions. The addition of the potential constraint as a weighted energy term in the agreement factor, allows reducing the occurrence of very unlikely, high energy configurations, and consequently, limits the spectrum of acceptable configurations and eliminates unrealistic features. A very important advantage added to this is the acquisition of thermodynamic consistency to the RMC models ¹⁵.

In this paper, the atomic configuration is a 20.647 Å length cubic box of 5000 atoms with periodic boundary conditions, including 3500 atoms of fluorine and 500 for each of the other species (Fe/V, Mn, and Ba). The resulting atomic density is about 0.0710 atoms/ų. Geometric and coordination constraints are used during the random distribution of constituents to generate the initial configuration as well as during the atomic random displacements to generate the new configurations after every test of χ values. First, each Fe atom has six (06) F neighbours between 0 and 2.20 Å and, second, each Mn atom has six (06) F neighbours between 0 and 2.40 Å. While running the HRMC code, we allow a maximum displacement of 0.08 Å for Ba and Fe, and 0.4 Å for Mn and F.

The idea of this paper is to use the obtained structural features such as the partial pair distribution functions (PDFs) g(r), to determine and to predict some structural and thermodynamic properties of the BaMnFeF₇ Fluoride glass.

3.Results and discussion

3.1.Structural property

3.1.1.Running coordination number nij(r)

The coordination number n _ij(r) of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it, obtained by integrating the respective partial pair distribution functions .

nij(r)=4πρ∫r2g(r)dr. (4)

Considering the anion-anion and anion-cation interactions, we represent the partial pair distribution functions (gXF(r), X = F, Fe, Mn, Ba ) in 2a), b), c) and d) respectively. We can initially verify the two constraints of coordination required for the FeF and MnF by calculating the number of the first near neighbour, using (4). For the FeF interaction: n _coord = 5.98 and n_coord = 6.18 for the MnF interaction, we observe the existence of the polyhedrons MnF₆ and FeF₆. These findings confirm the geometrical constraints used in the RMC simulation, each Fe atom has six (06) F neighbours between 0 and 2.20 Å and each Mn atom has six (06) F neighbours between 0 and 2.40 Å, (2b), and 2c)).

Figure 2 Partial pair distribution functions g _ij (r) by HRMC simulation, and running coordination number n _ij (r) of: a) FF, b) FeF, c) MnF and d) BaF at T _g = 572 K. 

The difference between the trainers FeF and the modifiers BaF appears clearly. The first peak around the trainers is narrow and well defined in Fig. 2b), which is indicative of a well-ordered local environment. However, for the modifiers, it can be seen that the appearance of the first peak is more spatially distributed with a lower intensity compared to the trainer in Fig. 2d), which means a greater distribution of local structures. While the distribution of MnF Fig.2c), has an intermediate characteristic between the trainers and the modifiers.

From the order point of view, we can classify the distributions as follows: gFeF(r), gMnF(r) and gBaF(r). So the MnF can play both the role of the trainers and the modifiers, hence the name of the intermediate element ¹.

3.2.Thermodynamic property

The thermodynamic properties of a system are described using a limited number of macroscopic variables such as the temperature T, the pressure P, the volume V and the number of particles N which depend on the statistical set used. In the grand canonical ensemble, they are connected to the partition function by the relation:

PV=kBTln Ξ. (5)

This relationship links the microscopic and macroscopic descriptions. The aim of this paper is to give the thermodynamic properties by using an analytical expression as a function of g(r).

3.2.1.Energy equation

The energy is an extensive variable that can be separated into a corresponding ideal part with perfect gas, therefore purely kinetic, and a part of the excess coming from interactions :

E=Eid+Eex. (6)

The interaction energy of a molecule with the molecules contained in an element of volume dr located at a distance r is: ρg(r)u(r)dr, and the sum of the interaction energies of a molecule with all the other molecules of the fluid is the integral over the entire volume,

ρ∫g(r)u(r)dr. (7)

For N molecules, the energy becomes:

N2ρ∫g(r)u(r)dr. (8)

The factor 1/2 takes into account the fact that each pair of molecules is counted twice. Furthermore, in spherical coordinates, we have dr=4πr2dr, the excess energy equation becomes:

Eex=2πNρ∫g(r)u(r)r2dr. (9)

Thus, the total energy of the liquid is written as follows:

E=32NkBT+2πNρ∫g(r)u(r)r2dr. (10)

From this equation, we can deduce the total energy of each interaction of the Fluoride glass. We are only interested in some important interactions FeF and MnF.

The first remark that we can draw about the potential is that it is purely attractive, for both interactions, FeF 3a) and MnF 3c). The partial pair distribution functions g(r) of the fluoride glass in question are deduced at Tg = 572 K (liquid state), therefore the relation which gives g(r) as a function of the potential u(r) is given by ^21,22:

g(r)=exp-u(r)+W(r)kBT, (11)

where W(r) is a function which depends on g(r). So the two Fig. 3a) and 3c) give the g(r) as a function of the interaction potential. We can notice that the potential for the MnF interaction begins to cancel at the distance of r = 5.25 Å, and at the distance of r = 6.25 Å for the FeF interaction. We can deduce the expression of W(r) as a function of g(r) at u(r) = 0. The W(r) represents the work of all constituents due to their motions around the equilibrium positions.

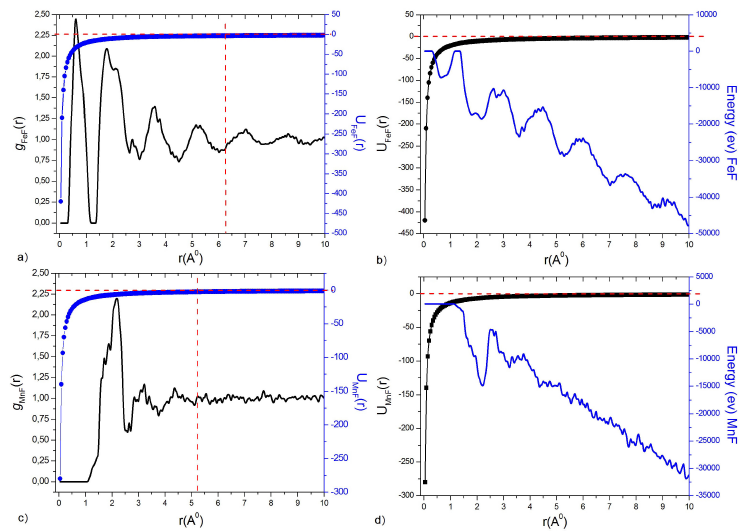
Figure 3 Potential of Buckingham u _ij (r), Radial pair distribution function g _ij (r) and the total energy E of : a), b) FeF and c), d) MnF at T _g = 572 K. 

Concerning the thermodynamic properties, we are interested in the total energy of the system, expressed by (10), and according to 3b) and 3d), we can conclude that EFeF>EMnF, and we confirm that the trainer remains the essential element in the formation of a glass, and the kinetic energy E _id for the two types of interaction is equal to 37 eV. The energy strongly depends on the chosen potential and the partial pair distribution functions g(r).

4.Conclusion

Based on the partial pair distribution functions g(r), calculated by the HRMC simulation using the Buckingham potential, the structural and thermodynamic properties for the BaMn(Fe/V)F₇ Fluoride glass system were calculated at T_g = 572K K.

The structural properties such as the coordination number n(r), computed by the RMC, show a good agreement with those provided by the Rietveld for RDM and confirm that the first coordinance neighborhood of Manganese, Mn and Iron, Fe is of six (6) F as considered by the coordination constraints.

In this work, we confirmed that the variation of the g(r) is a function of the potential u(r) and another term of energy W(r) through the comparison of the shape of the potential and that of the partial pair distribution function g(r).

For the thermodynamic properties, we calculate the energy of the system as a function of the partial pair distribution function g(r), which depends on the potential u(r). The chosen model takes into account the bonding environments. So we can conclude that the trainers always have the highest energy, followed simultaneously by the intermediate and modifier elements.

Finally the chosen potential is highly recommended for very complex systems to consider a maximum of the possible interactions.