1.Introduction
Mercury-cadmium telluride Hg1-xCdxTe and Mercury-Zinc Telluride Hg1-xZnxTe are two competitive materials used in infrared radiation detection 1,2. They have important applications in medicine and biology (laser IR, infrared camera) 3, in the industry (control of food products, rubber industry...) 4,5, and security (surveillance in military fields) 6. They are also used as Solar cells and photo-conductors 2-7-8. These are pseudo-binary semiconductors in the (II-VI) groups with small gaps and the same structural properties 9,10. The gap energies of the Hg1-xCdxTe alloys are between - 0.3 eV (HgTe) and 1.6 eV (CdTe) and fall within the infrared radiation energy range (IR) [ E ≤ 1.65eV]. However, the Hg1-xZnxTe possesses gap energies from -0.3 eV (HgTe) to 2.38 eV (ZnTe) and mechanical hardness that is greater than those of the Hg1-xCdxTe. These alloys are found to have the same nature of gaps 11,12.
Recently, M. Debbarma et al.,13 investigated the elastic and thermal properties of zinc Blende Hg1-xCdxTe ternary alloys using the FP-LAPW method. F. Kadari et al.,14 used WIEN2K code to study the structural properties of Hg1-xCdxTe and Hg1-xZnxTe alloys and the electronic properties of Hg1-xCdxTe and Hg1-xZnxTe alloys for X = 0.5 within the PBE-GGA and WC-GGA approximations in the zinc blende structure. The TB-mBJGGA potential combined with the PBE-GGA approximation was again used to study the electronic properties of the same materials. The results obtained are in agreement with experimental data. A. Laref et al.,15 studied the electronic structure, and optical characteristics of ZnHgTe alloys at concentrations x=0.25, 0.50, 0.75 by using the mBJ-GGA approach S. Al-Rajoub and B. Hamad 16 have studied the structural, electronic, and optical properties of the ternary alloy (X = 0.0, 0.25, 0.5 and 0.75), using WIEN2K code. In the same study, calculations of the structural properties are carried out with the LDA and GGA approximations for X = 0.0, 0.25, and 0.75 in the zinc blende structure and the tetragonal structure for X = 0.5. However, the electronic properties are determined with different approximations, namely: LDA, GGA, (LDA/GGA) + U, and (LDA / GGA) +mBJ. The mBJ+GGA approach gives better results for the electronic properties, except in the case of HgTe, where the GGA+U is better. The dielectric function was calculated using data obtained from the approximations giving the best gap values. B.V. Robouch et al 17 presented experimental results of the optical properties (dielectric function and reflectivity) of Hg1-xCdxTe and Hg1-xZnxTe for different concentrations. To our knowledge, there are no results published on the optical properties of Hg1-xZnxTe alloys for X = 0.25, 0.5, and 0.75 except Laref et al., 15. Moreover, there are no published results on the absorption spectrum of Hg1-xCdxTe, the refractive, and the reflection indexes of Hg1-xCdxTe (X=0.25, 0.75). Our contribution to the research topic is the use of two theoretical approaches, namely, the DFT and TB-mBJLDA for a detailed investigation of electronic and optical properties. To show the importance of the lattice parameter values in the computation of gap energy, the lattice parameter optimized either by LDA or GGA approximation has been used as an input parameter of the ‘TB-mBJLDA’ approach. As for the optical properties, a more comprehensive study and a detailed analysis of the optical coefficients, namely, the absorption spectrum, the refractive, and reflectivity index has been carried out an aspect that has found little interest in the published theoretical results in the literature.
The DFT is known for its underestimation of the gap energy 18, which has a direct impact on the computation of physical properties that are functions of gap energy, namely the linear optical properties 14. The option of using the DFT combined with the TB-mBJLDA potential 19 is considered, knowing that small variations of the lattice parameter values may generate important variations in the gap energy 20. In this work, the DFT (LDA and GGA) is used for the optimization of the lattice parameter of Hg1-xCdxTe and Hg1-xZnxTe for X = 0.0, 0.25, 0.5, 0.75, and 1.0. A comparative study of the electronic properties of these materials is carried out. It consists in performing a series of ab-initio calculations (LDA and GGA) with and without the TB-mBJLDA potential. Previous work using the TB-mBJLDA 21 has proved that the approach is successful for determining electronic and optical properties. Results from the first principle calculations are used to compute optical properties of Hg1-xCdxTe and Hg1-xZnxTe alloys in the zinc-blende structure at concentrations X in the range (0,1). The determination of the dielectric function will use data based on the approach giving the best gap energy. Our objective is to complete previous theoretical works regarding the structural, electronic, and mainly optical properties of Hg1-xCdxTe and Hg1-xZnxTe alloys for different values of X. In the following, the methodology is exposed, followed by an analysis of the obtained results and a conclusion.
2.Computational details
The method used in this work is the self-consistent full-potential linearized augmented plane wave (FP-LAPW) 22 as implemented in the ELK code 23, within the limits of LDA 24 and GGA 25 approximations. The study is concerned with the stability of HgTe, CdTe, ZnTe materials, and their ternary alloys Hg1-xCdxTe and Hg1-xZnxTe with concentrations X = 0.25, 0.5, 0.75, in the zinc blende structure.
The used values of muffin-Tin sphere radii (RMT) in (u.a) are 2.62 for (Hg and Cd)
and 2.42 for (Zn and Te). The K points grid in the Brillouin zone is chosen to be 14
x 14 x 14 and the maximum length of (G+K) vectors is fixed so that
Besides the use of LDA and GGA approximations, the study of electronic properties has required the use of the Tran-Blaha modified Becke-Johnson+LDA potential (TB-mBJLDA) 26, whose formulation is given by:
where c, is the added parameter by Tran and Blaha to the mBJ potential,
Optical properties were studied using the TB-mBJLDA approximation and a choice of lattice parameter values that guarantee the best gap energies in the range (0-24 eV).
3.Results and discussion
3.1.Structural properties
The equilibrium lattice parameter, the bulk modulus, and the derivative of the bulk modulus of the chosen materials are determined in the zinc blende structure where the binary alloys have the F-43m (2 1 6) space group, where Cd, Zn, or Hg atoms occupy the (0,0,0) position, and Te occupy the (0.25,0.25,0.25); however, the ternary alloys Hg1-xCdxTe and Hg1-xZnxTe (x = 0.25,0,5 and x = 0.75) are the results of the injection of Cd or Zn atoms in the unit cell of HgTe. The atomic positions of the different atoms and the different concentrations are reported in Table I; however, the crystal structures are shown in Fig. 1. The variation of the total energy as a function of the lattice volume of each alloy has been represented in the ET-lattice parameter (a) plane. The analytical expressions of these variations have been obtained by the Birch-Murnaghan 28 fit, whose equation of state is:
Table I Atomic positions of Hg 1-x Cd x Te and Hg1-x Zn x Te: ternary alloys.
| X | Atomes | Positions |
| 0.25 | Hg | (0, 0, 0), (0.5, 0, 0.5), (0.5, 0.5, 0) |
| Cd or Zn | (0, 0.5, 0.5) | |
| Te | (0.25, 0.25, 0.25), (0.75, 0.75, 0.25), (0.75, 0.25, 0.75), (0.25, 0.75, 0.75) | |
| 0.5 | Hg | (0, 0, 0), (0.5, 0.5, 0) |
| Cd or Zn | (0.5, 0, 0.5), (0, 0.5, 0.5) | |
| Te | (0.25, 0.25, 0.25), (0.75, 0.75, 0.25), (0.75, 0.25, 0.75), (0.25, 0.75, 0.75) | |
| 0.75 | Hg | (0, 0, 0) |
| Cd or Zn | (0.5, 0, 0.5), (0.5, 0.5, 0), (0, 0.5, 0.5) | |
| Te | (0.25, 0.25, 0.25), (0.75, 0.75, 0.25), (0.75, 0.25, 0.75), (0.25, 0.75, 0.75) |
Table II shows the structural properties of the binary materials: HgTe, CdTe, and ZnTe, which are compared with the available theoretical and experimental data. The lattice parameters obtained by the LDA approximation are close to the experimental values. However, those obtained by the GGA approximation are overestimated. The lattice parameters of HgTe, CdTe, and ZnTe are in good agreement with the theoretical 11-14-16-42 and experimental data 45-57-58-60. LDA calculations underestimate values of the lattice constants of HgTe, CdTe and, ZnTe, by about 0.23% (HgTe),0.10% (CdTe), and 1.78% (ZnTe) when compared to the experimental values of 6.46 A, 6.48 A, and 6,10 A17-43-45. However, GGA calculations overestimate values of the lattice constants of HgTe, CdTe and, ZnTe, by about 3.09% (HgTe), 3.9% (CdTe), and 1.29% (ZnTe) when compared to the experimental values 17-43-45. Values of the bulk modulus calculated by GGA are smaller than those values found by LDA approximation which are in good agreement with theoretical 11-14,42 and experimental data 59,51,45. Among the different compounds, it is found that ZnTe has the largest value of bulk modulus (53.09 GPa).
Table II Optimized lattice constant (a), bulk modulus (B) and bulk modulus derivative B´ of HgTe, CdTe, and ZnTe in zinc blende structure.
| Parameter | This work | Other works | |||
| Theoretical | Experimental | ||||
| LDA | GGA | 6.453d, 6.461g | |||
| HgTe | a (Å) | 6.445 | 6.66 | 6.644a, 6.6385b, 6.458c | |
| B (Gpa) | 46,3 | 32.35 | 35.57b | 42.3i | |
| B’ | 5.85 | 5.78 | 5.494b | ||
| CdTe | a (Å) | 6,487 | 6,734 | 6.421c, 6.614b, 6.42m | 6.467h, 6.48e |
| B (Gpa) | 41,91 | 35,15 | 42.12b, 44.41m | 42.4l | |
| B’ | 4.90 | 3.41 | 4.99b | 6.40l | |
| ZnTe | a (Å) | 5,997 | 6,179 | 6.174b, 5.98f, 5.99m | 6.009l, 6.103j |
| B (Gpa) | 53.09 | 41,182 | 52.21f , 51.62m | 51l, 50.50k | |
| B’ | 4.80 | 4.86 | 4.86f | 4.7l, 5.00k | |
a Ref. 16, b Ref. 14, c Ref. 37, d Ref. 57, e Ref. 43, f Ref. 11, g Ref. 17, h Ref. 58, i Ref. 59, j Ref. 60, k Ref. 51, l Ref. 45, m Ref. 42.
Results of the optimized equilibrium lattice constant and bulk modulus of Hg1-xZnxTe and Hg1-xCdxTe, obtained by GGA and LDA approximations for various x concentrations, are listed in Table III. For the lattice parameter, it is found that data relative to Hg1-xZnxTe and Hg1-xCdxTe alloys are in agreement with the theoretical and experimental results 14-17-44-58. It is observed that an increase in the composition X results in a lattice parameter increase. To the best of our knowledge, there are no bulk modulus experimental data available in the literature for Hg1-xZnxTe and Hg1-xCdxTe alloys in the range of X= 0.25 to X = 0.75. Figure 2 shows the plot of the lattice parameter of Hg1-xZnxTe and Hg1-xCdxTe alloys as a function of concentration X, as calculated by LDA and GGA approximations. It is found that an increase in the concentration x results in a nonlinear variation of the lattice parameter.
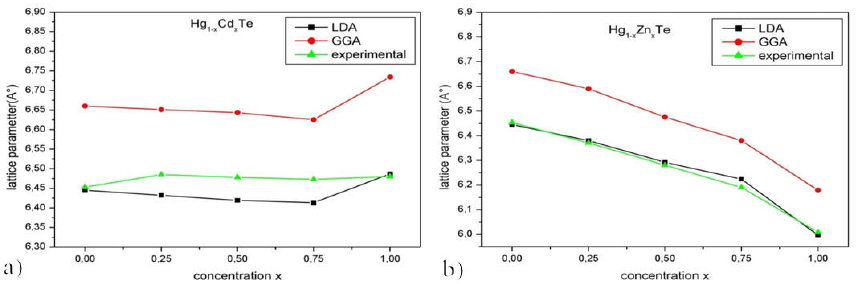
Figure 2 Lattice parameter variation of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys as a function of concentration x (LDA and GGA approximations).
Table III Optimized lattice constant (a), bulk modulus (B) and bulk modulus derivative B´ of ternary alloys Hg1-xCdxTe and Hg1-xZnxTe in zinc blende structure.
| Parameter | This work | Other works | ||||
| x | LDA | GGA | Theoretical | Experimental | ||
| a (Å) | 6.432 | 6,651 | 6.434a | 6.485d | ||
| x = 0.25 | B (Gpa) | 46.77 | 34.26 | |||
| B’ | 5.96 | 4.58 | ||||
| a (Å) | 6,419 | 6,643 | 6.6281b | 6.478d | ||
| Hg1−xCdxTe | x = 0.50 | B (Gpa) | 46,62 | 33.09 | 35.07b | |
| B’ | 6.19 | 4.79 | 4.96b | |||
| a (Å) | 6,413 | 6,625 | 6.416a | 6.473d | ||
| x = 0.75 | B (Gpa) | 48.38 | 34.12 | |||
| B’ | 5.18 | 5.10 | ||||
| a (Å) | 6,380 | 6,590 | 6.37075c | |||
| x = 0.25 | B (Gpa) | 49.56 | 36.03 | |||
| B’ | 4.70 | 4.57 | ||||
| a (Å) | 6,292 | 6.475 | 6.328b | 6.2805c | ||
| Hg1−xZnxTe | x = 50 | B (Gpa) | 51.18 | 41.03 | 37.85b | |
| B’ | 4.83 | 4.85 | 4.765b | |||
| a (Å) | 6,224 | 6,380 | 6.1902c | |||
| x = 0.75 | B (Gpa) | 54.91 | 42,35 | |||
| B’ | 4.21 | 4.44 | ||||
3.2.Electronic properties
LDA and GGA approximations are used to compute the band structure of HgTe, CdTe, ZnTe, and their ternary alloys based on Hg. The gap energies obtained from the band structure as well as other theoretical (DFT) and experimental results are reported in Table IV and plotted in Fig.3. Good agreement is observed between our results and the available theoretical data 11-14-16-42 and far from agreeing with experimental results 10-54-55-56. The under-estimation of gap energy is one of the problems associated with the use of the DFT (LDA or GGA) while studying electronic properties 18. Despite the fact of being in good agreement with other theoretical (DFT) studies, the values of band gaps of HgTe, CdTe, and ZnTe materials differ from the experimental values. Band gaps associated with the ternary alloys Hg1-xCdxTe and Hg 1-x Zn x Te are found experimentally to have low values. In this work, the DFT calculations give very low gap values for X = 0.75 and even negative values for X = 0.25 and 0.5. For Hg0.25Cd0.75Te, the values of gap energy agree with theoretical data 16,37 and differ slightly for Hg0.75Cd0.25Te and Hg0.5Cd0.5Te compounds. For Hg0.5Zn0.5Te, the values of gap energy are different from those reported in , which use the PBE-GGA approximation. To the best of the author’s knowledge, no theoretical (DFT) results regarding the gap energies of the band gaps of at X = 0.25 and X = 0.75 are found in the literature.
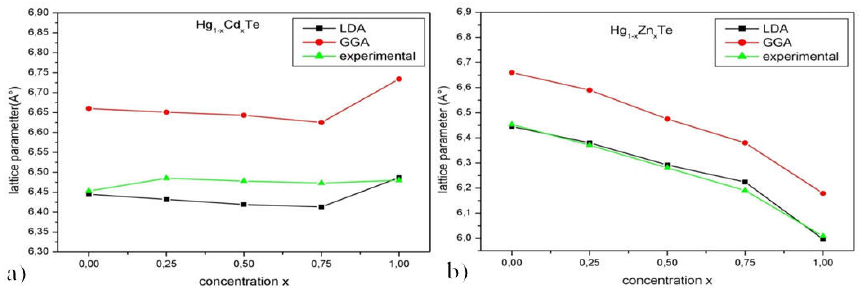
Figure 3 Gap energy variation of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys as function of concentration x (LDA, GGA + TB-mBJLDA and experimental data).
Table IV Gap energy values for binary and ternary alloys of Hg 1-x Cd x Te and Hg 1-x ZnxTe alloys for (x = 0:0, 0.25, 0.5, 0.75 and 1), using LDA and GGA approximations.
| Alloys | Material | This works | Other works | ||||
| Approximation | Gap energy (eV) | Gap nature | Theoretical (DFT) | Experimental | |||
| HgTe | LDA | −0.9074 | −0.907c | −0.3b | |||
| binary | CdTe | GGA LDA | −0.9318 0.501 | direct Γ − Γ | 0.59a, 0.48i | 1.606g | |
| GGA | 0.425 | direct Γ − Γ | |||||
| ZnTe | LDA | 1.2661 | direct Γ − Γ | 1.09a, 1.22i | 2.38g | ||
| x = 0.25 | GGA LDA | 1.05264 −0.5241 | direct Γ − Γ | 0.0f | 0.22h | ||
| GGA | −0.5579 | ||||||
| Hg1−xCdxTe | x = 0.5 | LDA | −0.1576 | 0.0c | 0.592h | ||
| GGA | −0.1997 | ||||||
| x = 0.75 | LDA | 0.21439 | direct Γ − Γ | 0.203c | 1.06h | ||
| Ternary | x = 0.25 | GGA LDA | 0.17872 −0.51398 | direct Γ − Γ | 0.380e | ||
| GGA | −0.5759 | ||||||
| Hg 1-x Zn x Te | x =0.5 | LDA | −0:0765 | 0.24d | 0.990e | ||
| GGA | −0:3421 | ||||||
| x =0.75 | LDA | 0.3922 | direct Γ - Γ | 1.621e | |||
| GGA | 0.3214 | direct Γ − Γ | |||||
a Ref. 11, b Ref. 56, c Ref. 16, d Ref. 14. e Ref. 10, f Ref. 37, g Ref. 54, h Ref. 55, i Ref. 42.
The same study has been extended to compute the band structure by using the Tran and Blaha modified Becke-Johnson potential (TB-mBJ) coupled with the LDA approximation and the insertion of the lattice parameters that have been optimized either by LDA or GGA approaches. The new gap energy values are reported in Table V. Comparison of the electronic properties data leads to ascertain that good agreement is observed between our results and other theoretical studies 14-16,29,15 for Hg 1-x Cd x Te and Hg 1-x ZnxTe alloys for (X = 0,0.25, 0.5, 0.75, and 1.0).
Table V Gap energy values of binary and ternary alloys of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys (x = 0:0, 0.25, 0.5, 0.75, and 1), using TB-mBJLDA potential.
| Material | This work | Otherworks | |||||
| Allaoys | Latticeparameter | Gap energy (eV) | Gap nature | Theoretical (mBJ or GW) | Experimental | ||
| Binary | Hg 1-x Cd x Te | HgTe | aLDA | −0.01968 | −0.701a, −0.03e, | −0.3h | |
| CdTe | aGGA | −0.1649 | −0.1f, −0.1g | ||||
| aLDA | 1.8137 | direct Γ − Γ | 1.541c, 1.57e | 1.606i | |||
| aGGA | 1.5273 | direct Γ − Γ | |||||
| ZnTe | aLDA | 2.6981 | direct Γ − Γ | 2.138c, 2.33f, | 2.38i | ||
| aGGA | 2.3253 | direct Γ − Γ | 2.2g | ||||
| x = 0.25 | aLDA | 0.4675 | direct Γ − Γ | 0.39a, 0.22e | 0.22b | ||
| aGGA | 0.2670 | direct Γ − Γ | |||||
| x = 0.5 | aLDA | 0,892 | direct Γ − Γ | 0.81a, 0.62e | 0.592b | ||
| Tenary | aGGA | 0.678 | direct Γ − Γ | ||||
| x = 0.75 | aLDA | 1,3486 | direct Γ − Γ | 1.27a | 1.06b | ||
| Hg 1-x Zn x Te | aGGA | 1.1360 | direct Γ − Γ | ||||
| x = 0.25 | aLDA | 0,5364 | direct Γ − Γ | 0.29c | 0.380d | ||
| aGGA | 0.3182 | direct Γ − Γ | |||||
| x = 0.5 | aLDA | 1.0729 | direct Γ − Γ | 0.773c, 0.72g | 0.990d | ||
| aGGA | 0.8526 | direct Γ − Γ | |||||
| x = 0.75 | aLDA | 1.6410 | direct Γ − Γ | 1.58c, 1.35g | 1.621d | ||
| aGGA | 1.4266 | direct Γ − Γ | |||||
a Ref. 16, b Ref. 55, c Ref. 14, d Ref. 10, e ref. 29. f Ref. 50, g Ref. 15, h Ref56, i Ref. 54.
The gap energy values obtained using the (TB-mBJLDA) approach are, generally, in agreement with the experimental results, which are plotted in Fig. 3, representing a clear improvement when compared to the simple DFT (LDA, GGA) results. Given that the gap energy value is very sensitive to small variations in the lattice parameter values, the use of aGGA instead of aLDA in the computation of gap energy of the binary materials HgTe, CdTe, and ZnTe lead to results that are comparable to the experimental data. The same observation is valid for the ternary Hg 1-x Cd x Te. However, for Hg 1-x Zn x Te, the best gap energies are obtained with aGGA for Hg0.75Zn0.25Te alloy and with aLDA for Hg0.5Zn0.5Te and Hg0.25Zn0.75Te alloys. Figure 4 shows the calculated electronic band structures of the binary materials: HgTe, CdTe, and ZnTe. The valence band maximum (VBMa) and the conduction band minimum (CBMi) for the considered compounds are located at Γ point. The band gap being direct and located at Γ- Γ. Figure 5 shows plots of the energy bands as calculated with the TB-mBJLDA for Hg 1-x Cd x Te. An almost linear increase of the gap energy is observed with increasing Cd concentrations (0.25 to 0.75). Hence, these alloys can be considered semiconductors with direct band gaps at the Γ-point. Plots of the electronic band structure of Hg0.5Zn0.5Te, for x = 0.25 to 0.75, using TB-mBJLDA correction are shown in Fig. 6. An increasing trend of the energy gap is observed with an increasing X.

Figure 4 Band structure of HgTe, CdTe, and ZnTe using TB-mBJLDA potential and aGGA lattice parameters.

Figure 5 Band structure of Hg 1-x Cd x Te alloy (x = 0:25, 5, and x = 0:75), using TB-mBJLDA and aGGA lattice parameters.
3.3.Optical properties
The complex dielectric function is the starting point for the computation of the
optical properties of different materials. These functions are completely determined
by the band structures of the considered materials. Hence, knowledge of the complex
dielectric function
In Fig. 7 and 8, the spectrums of the real and imaginary parts of the dielectric
function are represented. They summarize the optical processes resulting from the
interaction of an electromagnetic wave with a given material. Each material exhibits
a Mie resonance when

Figure 7 Spectrum of the real part of the dielectric function of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75 and 1).

Figure 8 Spectrum of the imaginary part of the dielectric function of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75 and 1).
The loss of electron’s energy, when moving in a given material, is defined by the
energy loss function L(ω) given in Fig 9, for
which the main peaks are associated with the Plasmon frequencies ωp
(

Figure 9 Energy loss function L(ω) of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75 and 1) as a function of energy.
The absorption coefficient α(ω) is related to the extinction coefficient K(ω) (5 and 7) and accounts for the average distance traveled by photons, before being absorbed in the material 35. For the binary alloys, absorption starts from energy values: 1.2 eV [HgTe], 1.85 eV [CdTe] and 2.68 eV [ZnTe]. It reaches maximal values at 6.30 eV [HgTe], 7.13 eV [CdTe] and 4.90 eV [ZnTe]. These results are comparable to those cited in 49. For the ternary alloy Hg 1-x Cd x Te (X=0.25, 0.5 and 0.75), the absorption starts at 1.58 eV, 1.43 eV and 1.77 eV, respectively. It reaches maximum values at 6.60 eV, 6.64 eV and 6.60 eV. In the case of the ternary alloy Hg 1-x Zn x Te (X = 0.25 0.5 and 0.75), the absorption starts at 1.20 eV, 1.85 eV and 2.34 eV, respectively. It becomes maximal at 6.30 eV, 6.68 eV, and 6.75 eV. Extinction coefficient and absorption coefficient spectrum are reported in Fig 10 and 11, respectively. The absorption coefficients relative to the ternary alloy Hg 1-x Cd x Te are found to agree with 15. For alloy, Hg 1-x Cd x Te the absorption coefficient spectrums, as reported in this work, are published for the first time and may constitute data to be compared within future works.
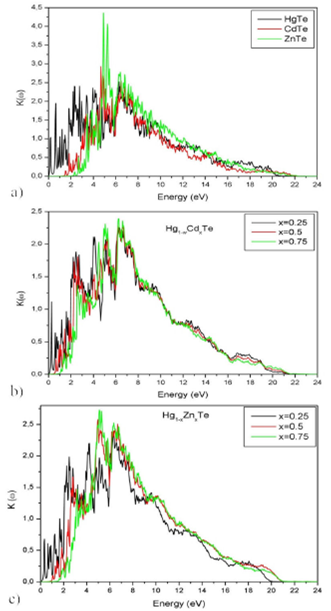
Figure 10 Extinction coefficient of Hg1-xCdxTe and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75 and 1) as a function of energy.
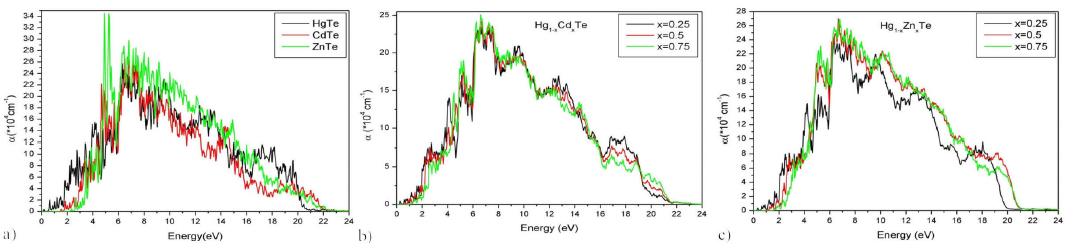
Figure 11 Absorption coefficient α (ω) of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75, 1) as a function of energy.
The refractive index n(ω) plot presented in Fig. 12 and that of the reflection coefficient R(ω) in Fig. 13 of the based HgTe ternary alloys shows a decreasing trend as a function of Cd and Zn concentrations. For a given frequency ω and for the binary materials: HgTe, CdTe, and ZnTe, the maximal values of the reflection coefficient fall into the Ultraviolet C (UVC) region. The same conclusion is valid for all concentrations X of Cd in the Hg 1-x Cd x Te and of Zn in the Hg 1-x Zn x Te materials.

Figure 12 Refractive index of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75 and 1) as a function of energy.
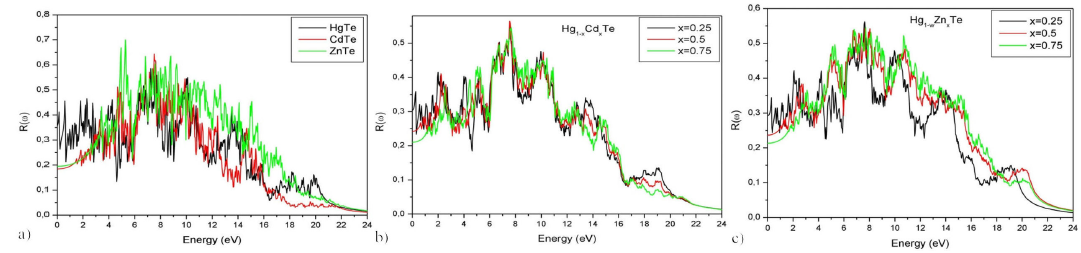
Figure 13 Reflectivity R(ω) of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys for (x = 0, 0.25, 0.5, 0.75 and 1) as a function of energy.
The refractive index n(ω), the reflection coefficient R(ω), and the static value ε1(0), associated with different alloys, are reported in Table VI and are represented, in Fig. 14, as functions of concentration x. The values of ε1(0) for CdTe, ZnTe, and Hg0.25Cd0.75Te are in agreement with the results of other theoretical works; however, for HgTe, ZnTe, Hg0.75Cd0.25Te and Hg0.5Cd0.5Te materials ε1(0) differ sensibly from the results reported in . It should be noted that for CdTe and ZnTe, the values of ε1(0) are in disagreement with the experimental results in Ref. 46 47. The calculated refractive index is in good agreement with other theoretical 29-31 and experimental 40-41-47 results for HgTe, CdTe, Hg0.5Cd0.5Te and Hg1-xZnxTe (for X = 0.25, 0.5 and 0.75). For ZnTe, the value of n(0) is in agreement with other theoretical results 31 but differs from the experimental data 40. Since no theoretical or experimental studies have been carried out on the optical properties, namely refractive index and reflection index of Hg0.75Cd0.25Te and Hg0.25Cd0.75Te, no conclusions can be drawn on the validity of our results, for they are still open to experimental verification.
Table VI Static dielectric function ε1(0), refractive index n(0) and reflectivity R(0) of Hg 1-x Cd x Te and Hg 1-x Zn x Te alloys, using TB-mBJLDA potential.
| Alloys | ε1(0) | n(0) | R(0) | |||||||
| Material | This work | Other works | This work | This work | Other works | |||||
| Theoritical | Experimental | Theorital | Experimental | |||||||
| Binary | HgTe | 15.85 | 16.9d,15,35j | 3.98 | 3.7e | 4.51g | 0.358 | 0.374a | ||
| CdTe | 6.27 | 6.7c | 10.31f | 2.50 | 2.55e | 3.26h | 0.184 | - | ||
| ZnTe | 6.65 | 6.75b, 7.1j | 9.63h | 2.58 | 2.5b | 4.5g | 0.194 | - | ||
| x=0.25 | 11.93 | 15.35c | - | 3.45 | 3.30e | 0.303 | - | |||
| Hg1−xCdxTe | x=0.5 | 8.62 | 10,41c | - | 2.93 | 3.00e | 3.13i | 0.242 | - | |
| x=0.75 | 7.25 | 7.53c | - | 2.69 | 2.74e | 0.210 | - | |||
| Tenary | x=0.25 | 11.71 | - | - | 3.422 | - | - | 0.300 | - | |
| Hg1−xZnxTe | x=0.5 | 8.36 | - | - | 2.892 | - | - | 0.236 | - | |
| x=0.75 | 7.37 | - | - | 2.716 | - | - | 0.213 | - | ||
4.Conclusion
In summary, the structural, electronic, and optical properties of Hg 1-x Zn x Te and Hg 1-x Zn x Te alloys were investigated using the full-potential linearized augmented plane wave (FP-LAPW). The study of structural properties of Hg 1-x Zn x Te and Hg 1-x Zn x Te materials, as done in this work, has confirmed that results obtained by the LDA approximation are better than those obtained by the GGA approach. The bulk modulus of Hg 1-x Zn x Te is greater than those of Hg 1-x Zn x Te alloys. The gap energies deduced from the band structures are underestimated by the LDA and the GGA for the two ternary alloys; however, they compare well to the experimental results when the mBJ-LDA potential is used. The same potential mBJ-LDA gives different values of gaps depending on the use of the lattice parameter aLDA calculated by the LDA approximation, or the use of the lattice parameter aGGA calculated by the GGA approximation. For all alloys, the coupling of mBJ-LDA potential with the lattice parameter aGGA, gives better results except for the case of Hg0.5Zn0.5Te and Hg0.25Zn0.75Te, where the use of the lattice parameter aLDA is preferable. For the binary and ternary alloys, the electronic properties, evaluated under either the LDA, GGA, or TB-mBJLDA potential schemes, are found to be those of semiconductors with direct band gaps at the Γ-point. The critical points of the optical constant spectrum (first peaks, main peaks, etc.) calculated from the dielectric function of Hg 1-x Zn x Te and Hg 1-x Zn x Te alloys are distinct. This distinction can be attributed to the difference in gap energies and the nature of the elements composing the different materials. In conclusion, one can say that the two ternary alloys possess comparable optical properties (refractive index, dielectric constant, and reflectivity). Results relative to the optical properties of the studied compounds could bear practical importance; especially, in applications such as microelectronic, optoelectronic, solar cell, and nuclear systems.











 nueva página del texto (beta)
nueva página del texto (beta)





