1. Introduction

Many microinhomogeneous materials, for instance, sedimentary rocks, contain a system of oriented or partially oriented inhomogeneities (inclusions). Thus, carbonate hydrocarbon reservoirs may be represented as a system of fluid-filled microcracks that are either randomly oriented or oriented along certain directions [^1-18]. The presence of such systems of cracks leads to a considerable anisotropy of the physical characteristics of the medium, such as effective electrical or thermal conductivity or elastic moduli. Identification of oriented systems of cracks and the evaluation of their parameters is an important problem that is of interest for many areas of physics of composite materials and petrophysics. The materials, containing high-conductivity inclusions, may be considered as homogeneous with certain effective properties, when their physical properties are determined in a larger scale compared to the characteristic size of inclusions.

During the past one hundred years, starting from the pioneering works by [^5,6,19] a number of methodologies of calculation of effective conductivity of a medium with inclusions of different shapes have been developed [^25-29]. A review of such methods that includes the works, published before 1990, was given in the papers by [^3,26,30]. An overview of the more recent works is given in Refs. [^4,29]. As a rule, in the majority of the works, that are based on the effective medium approach, the authors consider the media that contain either random or parallel inclusions. In the case of real media, such models may be frequently considered only as a rough approximation [¹⁸]. In the current work, we consider the model of a microinhomogeneous medium with inclusions that are not strictly oriented. Their spatial distribution is described by some angular function. Such models have long been in the interest of researchers. For elastic cracked solids, for example, such models are considered in Refs. [^15,28,31]. The solid review about the effect of orientation distribution on the effective properties of the fiber reinforced materials can be found in Ref. [²⁰]. In the works by [^8,9,17] the influence of the inhomogeneity orientation on the elastic and conductive properties of microinhomogeneous materials are studied. The results obtained in the last works were based on the so-called non-interaction approximation that slightly reduced the area of possible application. Our calculations are based on the so-named effective field method that allows considering the interaction between the inclusions. According to this method, every inclusion in the inhomogeneous medium is considered as an isolated one, embedded in the homogeneous background medium (matrix). The field that acts on this inclusion (effective field) does not coincide with the “external” field applied to the medium, but it is the sum of this “external” field and disturbances induced by all surrounding inclusions. This method has a long history, and it was mainly used in nuclear physics and the theory of phase transitions for the description of various types of many particle interactions. In application to the mechanics of composite materials, this method was developed by [^10,13]. This method has gained popularity for the calculation of effective elastic properties due to its simplicity. The most complete explanation of the method is given in the monographs by [¹³].

However, this method is not frequently used in application to the problems of thermal or electric conductivity. In our previous work by [¹⁶], we have applied this method to calculate the coefficients of the conductivity tensor of randomly oriented and parallel inclusions. In the present work, we apply the effective field method for the calculation of conductivity tensor of microheterogeneous media containing thin (crack-like) high-conductivity inclusions that are distributed in the space, and this distribution is characterized by some distribution density. In the second section of the paper, we discuss the homogenization problem, while in the third one we present the solution of the so-called one-particle problem that is the building block of any homogenization scheme. Then, the effective field method is shortly presented, and the effective conductivity of the material containing a random set of thin high-conductivity inclusions are calculated. After that we study the changes of the overall conductive material symmetry depending on the changes in the parameters of the distribution function over the orientation of the inclusions.

2. Homogenization problem

Let us consider a set of dispersed isotropic particles (inclusions), having the conductivity coefficient C, randomly distributed in an infinitely isotropic homogeneous medium, having the conductivity coefficient C ₀. The vector of the local flux q _i (x) and the field e_i (x) in such a medium satisfy the system of equations:

where x is an arbitrary point in 3D-space. These equations can describe various physical processes in solids, including stationary thermal conductivity and filtration, static electroconductivity in conductors and dielectrics, as well as, magneto- and electrostriction. All functions in Eqs. (3) are random functions of coordinates. Determination of the relation between the mathematical expectations of the fields qix and eix that generally has the form:

where Cij* is the tensor of effective (or overall) conductivity. The determination of this tensor is the central problem of micromechanics (the homogenization problem). For the random set of inclusions, the exact solution to this problem is impossible, and only approximate methods are available. There are several such approximate homogenization schemes that are named self-consistent methods [¹³]. The main distinguishing feature of these methods is the reduction of the problem for many randomly placed particles to the problem for only one separate particle (one-particle problem), that is the building block of these methods. In what follow, we consider a special kind of particle: the thin inclusion with high conductivity. Such inclusion can be used for example as a model of crack, filled with saltwater in a rock formation.

3. One-particle problem for a thin high-conductivity inclusion in a homogeneous medium

This problem has been solved by [¹⁶]. Here, we present this solution only briefly, the details can be seen in the mentioned publication. Let us examine a homogeneous isotropic medium having the conductivity coefficient C ₀, containing a single inclusion with the conductivity coefficient C, occupying the region v. The fields This problem has been solved by [¹⁶]. Here, we present this solution only briefly, the details can be seen in the mentioned publication. Let us examine a homogeneous isotropic medium having the conductivity coefficient C ₀, containing a single inclusion with the conductivity coefficient C, occupying the region v. The fields q _i (x) and e _i (x) satisfy the integral equations [¹⁶]:

where it is denoted

and qi0x are the “ external” fields that would be in the medium without inclusion; δx is the 3D-Dirac-delta function.

We assume that one characteristic length h of the region v is smaller than two others of order l. Thus the ratio δ ₁ = h/l is small. A thin inclusion with conductivity greater than that of the surrounding medium is of prime interest in application. In this case, the ratio δ ₂ = C₀/C is also small. The most valuable information about the fields e_i (x) and q _i (x) in the vicinity of the inclusion is contained in the principal terms of the asymptotic expansion of these fields over the parameters δ ₁ and δ ₂. In order to construct these terms, it is necessary to find the limiting solution of the conductivity problem, when δ ₁ ,δ ₂ → 0, and the ratio δ ₁ /δ ₂ is of unit order and remains constant.

Let us assume that the middle surface of the inclusion Ω is a smooth enough surface with a given continuous field of its normal vector n _i (x). The surface Ω bounded by the closed contour Γ. We take a point x on Ω and put it in the origin of the local coordinate system with We assume that one characteristic length h of the region v is smaller than two others of order l. Thus the ratio δ ₁ = h/l is small. A thin inclusion with conductivity greater than that of the surrounding medium is of prime interest in application. In this case, the ratio δ ₂ = C ₀ /C is also small. The most valuable information about the fields e _i (x) and q _i (x) in the vicinity of the inclusion is contained in the principal terms of the asymptotic expansion of these fields over the parameters δ ₁ and δ ₂. In order to construct these terms, it is necessary to find the limiting solution of the conductivity problem, when δ ₁ ,δ ₂ → 0, and the ratio δ ₁ /δ ₂ is of unit order and remains constant. Let us assume that the middle surface of the inclusion Ω is a smooth enough surface with a given continuous field of its normal vector We assume that one characteristic length h of the region v is smaller than two others of order l. Thus the ratio δ ₁ = h/l is small. A thin inclusion with conductivity greater than that of the surrounding medium is of prime interest in application. In this case, the ratio δ ₂ = C ₀ /C is also small. The most valuable information about the fields e _i (x) and q _i (x) in the vicinity of the inclusion is contained in the principal terms of the asymptotic expansion of these fields over the parameters δ ₁ and δ ₂. In order to construct these terms, it is necessary to find the limiting solution of the conductivity problem, when δ ₁ ,δ ₂ → 0, and the ratio δ ₁ /δ ₂ is of unit order and remains constant.

Let us assume that the middle surface of the inclusion Ω is a smooth enough surface with a given continuous field of its normal vector n _i (x). The surface Ω bounded by the closed contour Γ. We take a point x on Ω and put it in the origin of the local coordinate system with z-axis directed along the normal n _i (x). We denote by h(x) the transverse size of the inclusion along the normal n _i (x). Then, we denote h(x) = δ ₁ l and take into account that δ ₁ /δ ₂ is O(1). It follows from Eqs. (3.1) that the main terms of the field expansion of e _i (x) and q _i (x) over δ ₁ and δ ₂ in the medium with thin high-conductivity inclusion can be expressed as:

where

and it is necessary to consider the main terms of expansion over δ ₁ and δ ₂ in the expansion for η _i (x). To construct these terms (for which we will preserve the same notation η _i (x)), we will use the method of matched asymptotic expansion. Using the results of [¹²], where one can find the details of the proof, it is possible to show that η _i (x) is the vector of the surface Ω satisfying the equality:

This vector is the solution of the following integral equation:

where it is denoted

and the action of the operator with kernel U_ij (x,x⁰) on a smooth enough function (regularization of this operator) can be obtained in Ref. [¹²].

Solving (3.6) for the function ηix and substituting the result in the right-hand side of (3.3), we obtain expressions for the field eix and qix. These fields approximate the real fields in the medium with inhomogeneity except for the small vicinity of the contour Γ. For an inclusion of arbitrary shape, (3.6) can be solved only numerically. But for ellipsoidal thin inclusion and constant “external” field ei0 this equation can be solved in the closed analytical form.

Let the inclusion be a thin ellipsoid with semi-axes a1,a2,h,(h/a1,h/a2≪1. Then Ω becomes a plane elliptical surface. Let ni denotes its normal. In the system of coordinates with the axes that coincide with the major ellipsoid axes, function hx can be written as:

In the results of calculations, the details of which are presented in Appendix A, we obtain that the fields eix and qix outside of the thin inclusion can be expressed as:

Here, Zx is denoted

and tensor Λ _ij in same system of coordinates with unit vectors n ¹ _i ,n ² _i ,n ³ _i (n ³ _i is coincided with the normal n _i of the surface Ω) has the form:

where

K(k) and E(k) are the complete elliptic integrals of the first and the second kind, respectively:

4. Random set of thin low-resistivity inclusions in an isotropic homogeneous medium

We consider a microinhomogeneous medium consisting of a homogeneous isotropic host material (matrix) and random set of thin low-resistivity inclusions. The “one-particle” problem, considered in the previous Section, is basic for self-consistent homogenization schemes [^11,13]. Here, we use one of these schemes that is named the effective field method (EFM). According to this method, we introduce a local “external” field ei*x that acts on each inclusion. This field is composed of an “external” field ei0 and the fields induced by surrounding inclusions. The main hypothesis of the effective field method is as follows: every inclusion in the composite material can be considered as an isolated one in the homogeneous matrix in a local uniform “external” field ei*, which depends on the orientation of the inclusion (vector n). Using this hypothesis, the expressions for the fields eix and qix can be represented in a form like Eqs. (3.3), in which:

Here, Ωkx is a generalized function concentrated on the surface of the k-th inclusion, the function nx coincides with the normal n to the surface Ωk, when x∈Ωk. The function Λijx is equal to the constant value Λija1k,a2k determined in (3.11), when x∈Ωk and:

The procedure of the homogenization by the effective field method is presented in Appendix B. The final result is:

where ⋅ means the averaging over ensemble distribution of the sizes and orientation of the inclusions; n0 is the number concentration of the inclusions. Tensor Aijn in (4.3) is determined by the relations:

where α1,α2,α3 are the semi-axes of the ellipsoidal “correlation hole” (see Appendix B).

The cases of parallel and completely disoriented thin high-conductivity inclusions were considered by [¹⁶]. In what follows, our attention is concentrated on the effects of partly oriented inclusions.

5. Description of the inclusion orientation distribution

For the description of the thin inclusion orientation, we introduce a global Cartesian basis eii=1,2,3 of the axes x1,x2,x3, where x3 is the vertical axis (Fig. 1). The orientation of the basis nkk=1,2,3 that defines the symmetry axes of the elliptical thin inclusion with respect to the global basis ei is described by the three Euler angles ψ,θ,φ, and the connection between these bases is given by the relations:

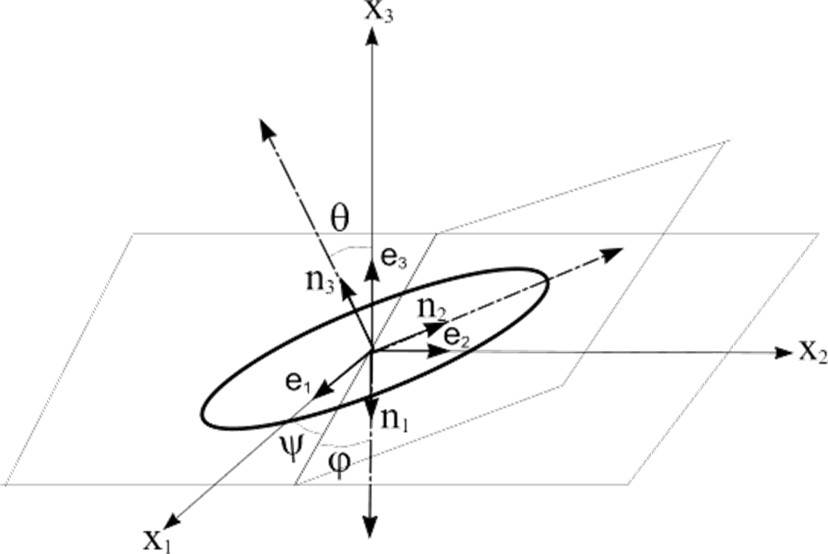
FIGURE 1 The global basis is e_i , and the basis n_i defines the symmetry axes of the elliptical crack-like inclusion, (ψ,θ,ϕ) are the Euler angles.  

Substituting these formulas into (4.3), we obtain the presentation of the tensor Cij* in the global basis ei.

Let us consider some special cases.

Let the thin inclusions be the same size and shape, but randomly oriented with respect to the global coordinate system. In this case, the formula (4.3) takes the form:

and the Euler angles in Eqs. (5.1) become random variables. The parameter τ in Eq. (5.2) is the so-called crack density.

We introduce the function of distribution fψ,θ,φ of the inclusion orientation over the angles ψ,θ,φ. This function must satisfy the normalization conditions:

Suppose that the orientations of the inclusions, described by the angles ψ,θ,φ, are statistically independent. Therefore, the function fψ,θ,φ can be represented as:

The normalization conditions take the form:

We consider the case, when fψψ=1, fφφ=1, fθθ≠1. The medium has the macroscopically transversely isotropic conductive properties with symmetry axis x3:

where it is denoted:

The case fθθ=1 (the uniform distribution over the angle θ) leads to Sθ=1/3, that corresponds to the full isotropy of the material:

6. Numerical examples

To validate our model, we calculated the effective conductivity of the medium, which contains parallel spheroidal inclusions, using the effective field method and the well-known Effective Medium Approximation (EMA) by [^3,4,5]. The semi-axes of the inclusions were chosen as a ₁ = a ₂ = 1, a ₃ = 0.001. The inclusions conductivity is equal to 1, and the matrix conductivity is equal to 0.01. To compare the results obtained with the EMA model and the effective field method, we use the inclusion concentration Φ instead of the crack density τ. For spheroidal inclusions τ = 3Φ/(4πα), where α is the aspect ratio of the spheroid. The comparison of the results obtained shows that both methods give close results for parallel inclusions [Fig. 2], but to calculate the effective conductivity of the material with partially oriented inclusions by the EMA method is a complicated mathematical problem,while the (EFM) gives the explicit expressions for the effective conductivity coefficients.

FIGURE 2 Effective conductivity as a function of the inclusion concentration. The calculations are presented for parallel spheroidal inclusions.  

Further, we present examples of the effective conductivity calculation for partially oriented inclusions. We assume that the inclusion conductivity is equal to 1, and the matrix conductivity is equal to 0.01. The semi-axes of the inclusions were chosen as a ₁ = 1, a₂ = 0.5, a₃ = 0.01. Such parameters are typical, for example, for sedimentary carbonate rocks containing cracks, filled with conductive formation water [¹]. We assume that the correlation hole has a spherical shape: A ₁ = A₂ = A₃ = 1. Figures 3 and 4 show the dependences of the conductivity tensor components of the horizontal and vertical crack-like inclusions, homogeneously distributed in the sector [−β,β], where β is the disorientation angle. The angle distribution function is described by (5.11). The calculations were fulfilled for the disorientation angle θ = π/2 and θ = 0(ϕ = 0) for vertical and horizontal inclusions, respectively. The aspect ratio of the correlation hole is close to 1. As expected, the effective medium is orthorhombic C1*≠C2*≠C3*, but with increasing of the value of the parameter β the difference between the conductivities C1* and C2* decreases. When the β value is close to π/2, the difference between C1* and C2* tends to zero, and the medium becomes transversely isotropic (Figs. 3 and 4).

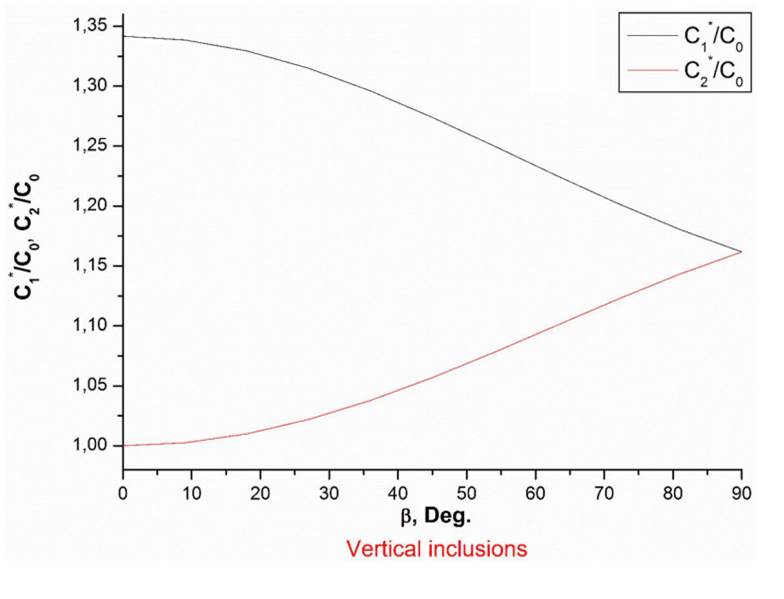
FIGURE 3 Normalized components of the conductivity tensor as a function of the disorientation angle β. The crack density τ = 1. The results are presented for the system of vertical inclusions (θ = π/2, ϕ = 0) and the first model of the angular distribution (inclusions homogeneously distributed in the sector [−β,β]). 

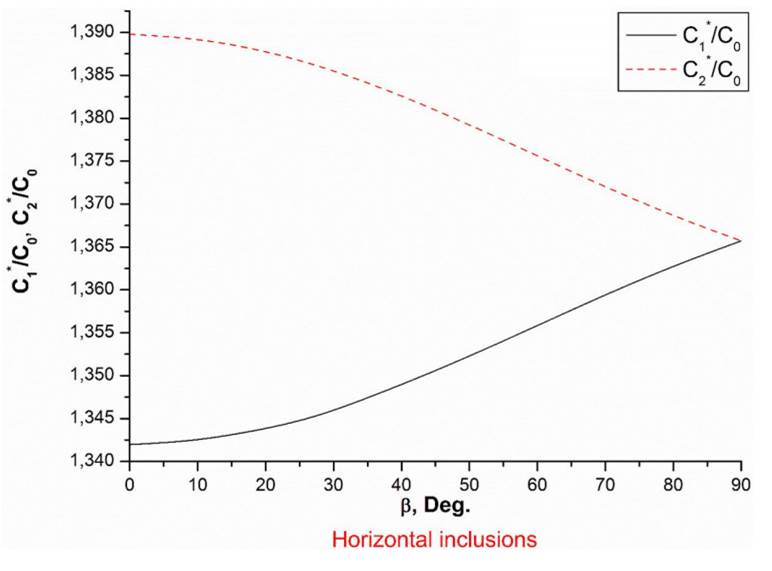
FIGURE 4 Normalized components of the conductivity tensor as a function of the disorientation angle β. The crack density τ = 1. The results are presented for the system of horizontal inclusions (θ = 0, ϕ = 0) and the first model of the angular distribution (inclusions homogeneously distributed in the sector [−β,β]).  

Figures 5-6 show the dependences of the normalized components of the conductivity tensor as a function of the disorientation parameter σ (the distribution function (5.21). The results are presented for vertical and horizontal cracklike inclusions. In the general case, the effective medium is orthorhombic, but in the case, when σ→∞, the effective medium becomes transversely isotropic.

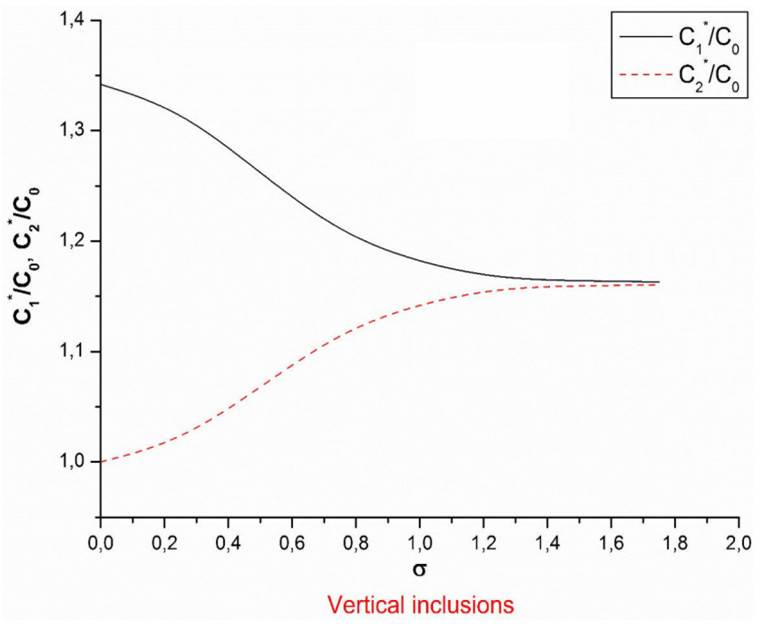
FIGURE 5 Normalized components of the conductivity tensor as a function of the disorientation parameter σ. The crack density τ = 1. The results are presented for the system of vertical inclusions (θ = π/2, ϕ = 0) and the second model of the angular distribution of the inclusions (Eq.(5.21)).  

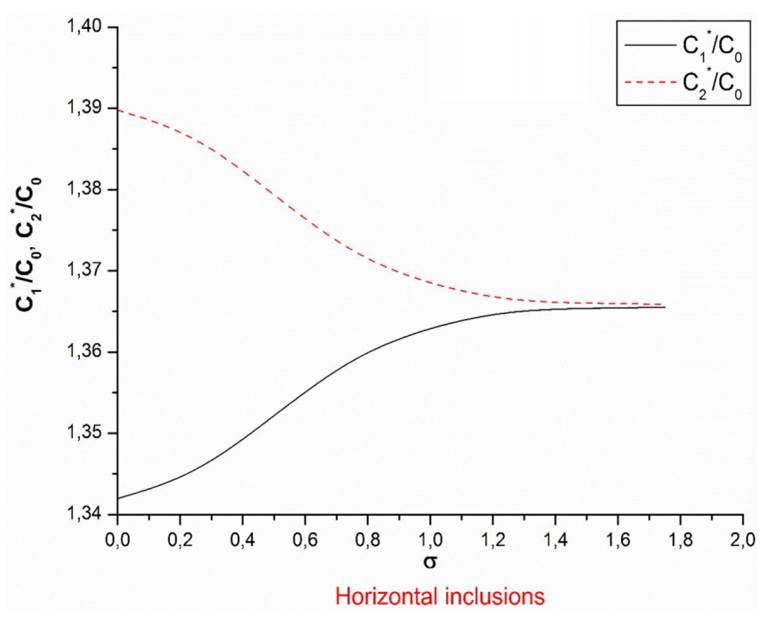
FIGURE 6 Normalized components of the conductivity tensor as a function of the disorientation parameter σ. The crack density τ = 1. The results are presented for the system of vertical inclusions (θ = 0, ϕ = 0) and the second model of the angular distribution of the inclusions (Eq.(5.21)).  

Figure 7 illustrates the dependences of the normalized components of the conductivity tensor as a function of the disorientation angle β for different crack densities. The results are presented for vertical inclusions. In the general case, the effective medium is orthorhombic, but in the case, when β=π/2, the effective medium becomes transversely isotropic.

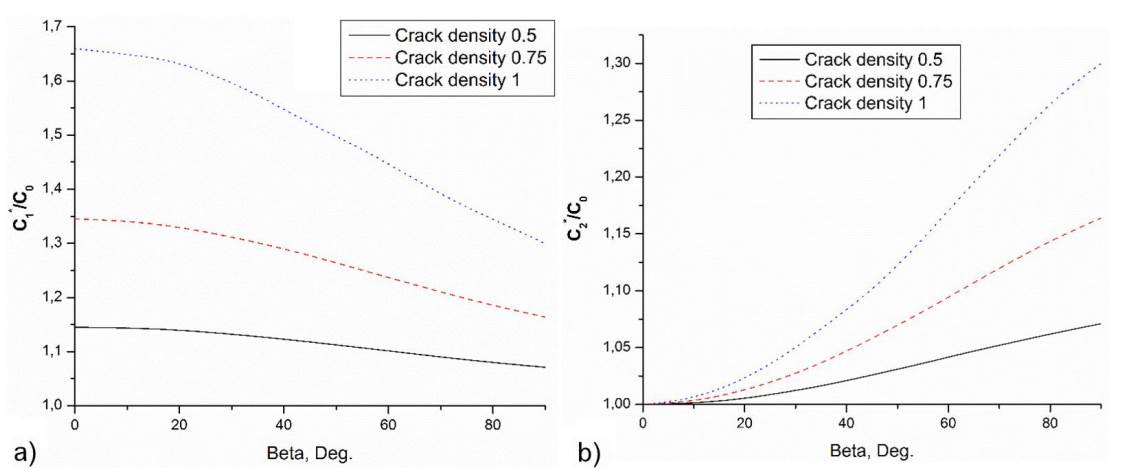
FIGURE 7 Normalized components of the conductivity tensor as a function of the disorientation angle β. Different curves correspond to the different values of crack densities. Figure 7A corresponds to the conductivity in the direction x ₁, and Figure 7B corresponds to the conductivity in the direction x ₂. The results are presented for the first model of angular distribution (inclusions homogeneously distributed in the sector [−β,β]).  

7. Conclusion

We have presented an approach for calculating the effective conductivity tensor of material containing a system of cracks that are not strictly oriented. Their spatial distribution is described by some angular function. The approach is based on the effective field method. This method is sufficiently general and contains the well-known method of Mori-Tanaka and the Maxwell method as particular cases. The advantage of the effective field method lies in its simple numerical realization compared with other methods. The application of this method permits us to take into account the texture of a microinhomogeneous medium. The general theory was illustrated by numerical results obtained for crack-like inclusions homogeneously distributed in the sector. We have shown that in the case of circular penny-shaped inclusions with the same aspect ratio, the effective medium can be orthorhombic, transversely isotropic, or isotropic depending on the choice of the distribution function of the normal to the crack surface from Euler angles. From our point of view, the dependences, obtained in the framework of this work, may be interesting for many areas of applications, including the rock physics and physics of micro-inhomogeneous (cracked) materials.