1. Introduction
Elastic scattering processes between two colliding nuclei still remain an important topic in nuclear physics studies. The scientific community has been attracted to 4,6,8He because of its special aspects in scattering with heavy targets. The weakly bound nucleus 6He has a broad neutron distribution and a low 2n-binding energy, which is well known[1-4]. These characteristics favor neutron transfer and breakup, and therefore should affect the angular distribution of elastic cross sections [5-9]. 8He has more valence neutrons but is more tightly bound, with binding energies comparable for 1n and 2n systems, whereas 6He favors two-neutron breakup. The elastic and reaction cross sections for collisions with heavy targets at Coulomb barrier energies are expected to reflect the differences between the two helium isotopes.
A. M. Sanchez-Bentez et al [5] analyzed data of elastic scattering of 6He+208Pb measured at laboratory energies of 14, 16, 18, and 22 MeV using phenomenological Woods Saxon form factors and optical model calculations. The dispersion relations that connect the real and imaginary parts of the optical potential were found to be consistent with the energy variation of the optical potential.
The goal of this research is to see how sensitive 4,6,8He + 208Pb elastic scattering is to various phenomenological and semi-microscopic potentials [10-16]. Various models have been used to explain nuclear-particle interactions.
Some of these approaches include the double-folding model (DFM), the Woods-Saxon (WS) potential, and various variations of the WS potential. However, for analyzing experimental angular distributions of low-energy scattering of exotic nuclei on stable nuclei, the well-known double-folding (DF) model is the most widely used method. The phenomenological OM as well as the DF with the appropriate optimized parameter sets accurately reproduce the elastic scattering angular distributions for 4,6,8He + 208Pb elastic scattering. We reanalyzed the experimental data of the 4,6,8He + 208Pb reaction at 22 MeV [8-16] by calculating the nuclear potential using a variety of potentials, including Sao Paulo potentials, CDM3Y6 potentials with and without the rearrangement term (RT), and phenomenological WS potentials [17-22].
The paper is organized as follows. Section 2 discusses the nuclear potentials that are used in the data analysis, while Sec. 3 discusses the results and discussion. The summary is provided in Sec. 4.
2. Theoretical methods
As a first step for probing the interaction mechanism for the considered nuclear systems, OM of the nucleus is applied. The implemented phenomenological OM potential has the following form:
The V
c
(r) is the Coulomb potential due to a uniform sphere with a charge equal to that of the target nucleus and radius r
c
According to the different parameter ambiguities both discrete and continuous associated with the OM calculations, and the fact that phenomenological representations do not include a description of the projectile or target’s structure, the real part of potential was constructed using the microscopic double folding (DF) procedure extracted from the CDM3Y6 interactions with and without rearrangement term RT as well as Sao Paulo potential (SPP) via the double convolution integral
where
R = 6.8 fm , a = 0.515 fm and root-mean-square (rms) matter radius of 5.604 fm, respectively while ρ 0 can be determined from the normalization condition.
The DF potential consists mainly of two parts:
The direct part is
and the knock-on exchange part in the infinite-range exchange is
In this study, a modified version of the CDM3Y6 interaction is used, which includes the rearrangement term (RT) (CDM3Y6-RT). The density-dependent version (CDM3Y6) of the M3Y effective NN interaction based on the G-matrix elements of the Paris potential is used for the direct and exchange terms in Eqs. (5) and (6). [21], which is the full CDM3Y6 interaction form.
where, the density dependent function F is written as [21]
And g(E) is the additional energy dependent factor written as [21],
The term ΔF(ρ) is added to the folding model calculation for the modified (CDM3Y6-RT) interaction with the inclusion of the RT term, where ΔF(ρ) can be written as [29],
In the SPP model, the following two equations link the real part of the local-equivalent interaction to the DF potential V F (R) as
where ρ p (r p ) and ρ T (r T ), respectively are the nuclear matter density distributions for the two colliding nuclei. The following two equations link the real part of the local-equivalent interaction to the DF potential V F (R) as
Where V is the nuclei’s local relative velocity and C is the speed of light. The nuclear densities were obtained from the Dirac-Hartree-Bogoliubov model [30], and the Sao Paulo potential (SPP2) was calculated using the REGINA code [20].
3. Results and discussion
For incident energies of E tab = 22 MeV, elastic scattering results for the 4,6,8He + 208Pb reactions were obtained. Three different theoretical approaches were used for this purpose microscopic double folding model based on Sao Paulo potential, CDM3Y6 interaction with and without RT, and phenomenological Woods Saxon (WS) model. The potentials that resulted are represented in Fig. 1. The comparisons between the experimental 4,6,8He nuclei elastically scattered from a 208Pb target at E = 22 MeV and the theoretical calculations using both phenomenological OM and microscopic model are shown in the Fig. 2.
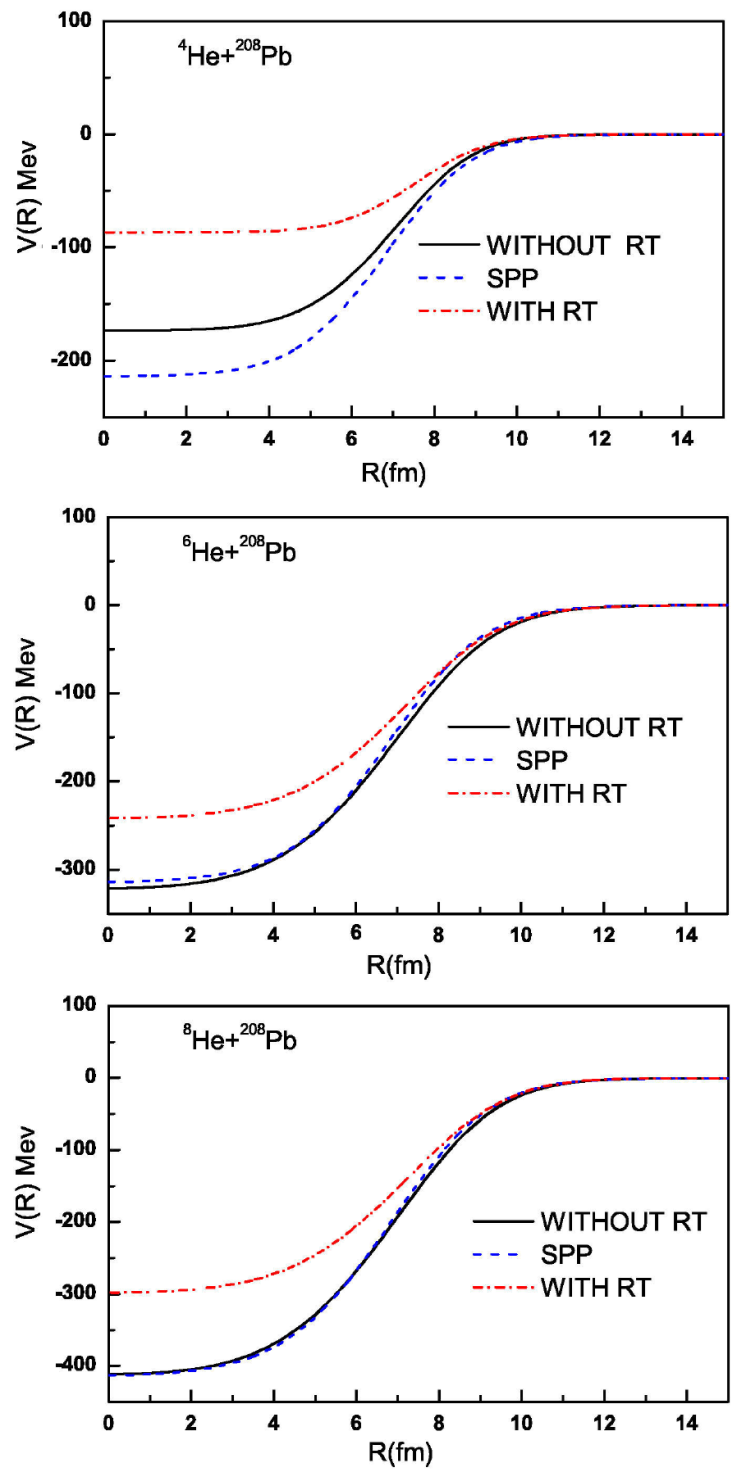
Figure 1 The generated real SPP as well as CDM3Y6 with and without RT for 4,6,8He + 208Pb target at E tab = 22 MeV.
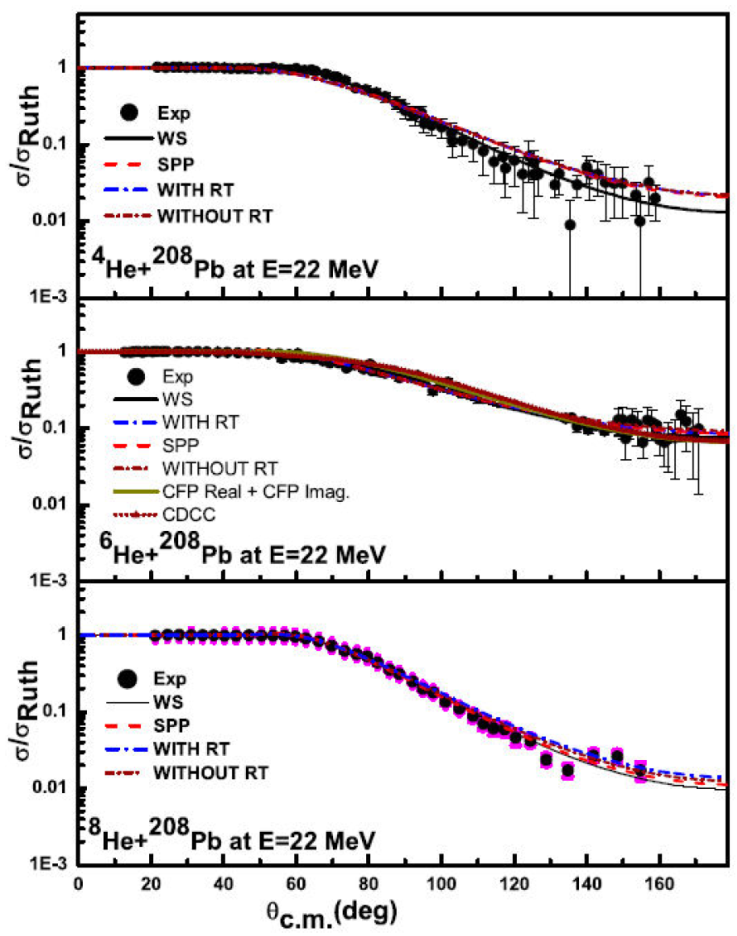
Figure 2 Comparison of experimental angular distributions (solid black circles) and theoretical calculations (solid red curves) for 4,6,8He+ 208Pb elastic scattering using WS and real folded potential at E tab = 22 MeV. Ref. [10-16] provided the experimental data. Cluster folding potential for 6He+ 208Pb is performed by considering triton + triton cluster structure for 6He as well as the CDCC calculations.
For the real and imaginary potentials, three parameters were used in the OM computations. Depths, radius, and diffuseness for the real (v 0, r 0, a 0) and imaginary (w 0, r w , a w ) volume parts of the interaction potential were freely changed until the best fit for the data was achieved by minimizing the χ 2 value defined by
where N is the number of data points, σ(θ i ) cal and σ(θ i ) exp are the calculated and experimental differential cross sections (DCs) and Δσ(θ i ) is the relative uncertainty in experimental data.
The parameters with the best fit are listed in the table. The theoretical fits were done with the FRESCO code [27], and the optimal potential parameters were found with the SFRESCO search code. For the 6,8He, it is obvious that the agreement between theoretical results and experimental data is almost perfect. The results of the 4He+ 28Pb reaction, in particular, are shown to be almost excellent for the WS model, which properly represents the experimental data for both small and large angles. However, the conclusions of the SPP and CDM3Y6 models for all incidence energy exclude some angles of the experimental data.
For each reaction, we calculated volume integrals as well as chi square χ 2 values. Using various versions of the nuclear model of the 4,6,8He nucleus, we found that the phenomenological potential (WS) with 6-free parameters provides good fitting for all systems, as evidenced by the chi square values in Table I, whereas the other microscopic potentials, the obtained values for the chi square value give a closed value to each other. Real real (J R ) and imaginary (J I ) volume integrals are used to calculate the volume integral. The J R and J R volume integrals are crucial for demonstrating the evaluated potential’s strength. In this context, the Table shows the J R and J I values for the WS, SPP, and CDM3Y6 models. It has been found that altering the used model results in similar J R and J R values. The smallest values for the WS results can be seen when the χ 2 values are examined. Of course, a lower chi square χ 2 value corresponds to a more accurate description description of the experimental data in terms of the chosen theoretical representation. As a result, similar cross sections for various approaches can indicate similar experimental results [6-12]. As a result, it is reasonable to assume that various approaches have resulted in a successful analysis of the experimental data.
Table I The Optical potential parameters obtained from analysis of the 4,6,8He + 208Pb elastic scattering at E = 22 MeV using WS, folded potential based on CDM3Y6 with and without rearrangement term, Sao Paulo potential (SPP), as well as cluster folding potential (CFP). Volume depth (V 0, W 0), radius and diffuseness parameters (r i , a i ), i = v, w. “Real and imaginary volume integrals (J R and J I ), total reaction cross section (σR) and the best fit χ2 are presented.
| Model | V(N r ) | rV | a V | W | rW | a W | χ2/N | σ R | J R | J I |
|---|---|---|---|---|---|---|---|---|---|---|
| 4He+ 208Pb | ||||||||||
| WS | 9.442 | 1.850 | 0.850 | 9.11 | 1.850 | 0.7932 | 0.759 | 1255 | 66.32 | 63.52 |
| SPP | 1.0 | 6.178 | 1.850 | 1.306 | 1.688 | 1661 | 399.29 | 46.46 | ||
| RT | 1.0 | 7.319 | 1.850 | 1.2658 | 1.972 | 1693 | 196.32 | 54.86 | ||
| RT=0 | 0.95 | 7.303 | 1.850 | 1.266 | 1.984 | 1693 | 335.68 | 54.74 | ||
| 6He+ 208Pb | ||||||||||
| WS | 23.72 | 1.4817 | 0.8501 | 139.99 | 1.850 | 0.300 | 3.05 | 1159 | 88.28 | 935.06 |
| SPP | 0.996 | 139.62 | 1.5949 | 0.850 | 2.543 | 1280 | 400.1 | 640.53 | ||
| RT | 0.998 | 39.365 | 1.850 | 0.7382 | 2.822 | 1333 | 350.89 | 272.69 | ||
| RT=0 | 0.995 | 39.205 | 1.850 | 0.7420 | 2.835 | 1340 | 430.47 | 271.70 | ||
| CFP | 0.1 | 3.0 | 3.0 | 1330 | 43.2 | 187.4 | ||||
| 8He+ 208Pb | ||||||||||
| WS | 17.15 | 1.5456 | 0.850 | 139.91 | 1.850 | 0.6506 | 5.33 | 1461 | 71.94 | 959.92 |
| SPP | 0.95 | 137.95 | 1.5834 | 0.7975 | 7.13 | 1408 | 286.75 | 614.38 | ||
| RT | 1.0 | 149.99 | 1.5834 | 0.7975 | 7.74 | 1412 | 326.30 | 668.01 | ||
| RT=0 | 1.06 | 149.99 | 1.5834 | 0.7975 | 6.84 | 1420 | 439.12 | 668.01 | ||
To validate our analysis, we plotted expression (12) at 22 MeV for 4,6,8He+ 208Pb and, against the DF potential with finite-range exchange contribution for the densities under consideration, as shown in Fig. 1. At the center (R=0),
A strong absorption radius R
S
(closest approach) through the surface radial region can be defined as the distance between colliding particles in terms of the transmission coefficient T
1/2, which is a function of the partial wave and momentum L1/2, as well as the Sommerfield parameter
3.1 Cluster folding Potential for 6He+ 208Pb
Cluster folding (CF) potential obtained from the t + t probable cluster structure for 6 He + 208 Pb elastic scattering data is used to fit the data. Based on the suggested t + t model, the real and imaginary CF potentials for 6He + 208Pb system can be defined on the basis of t + 208Pb potentials as: the real and imaginary CF potentials for the 6He + 208Pb system may be defined on the basis of t + t model. Using the recommended t + t model as follows, we can write the 6He + 208Pb potential as
The
The 6He + 208Pb experimental angular distribution at E = 22 MeV “see Fig. 2” is reanalyzed within the framework of cluster folding model using two adjustable parameters N RCF and N ICF , namely the renormalization factor for the real and imaginary cluster folding potentials, respectively, derived based on Eq. (14) and presented in Fig. 1. The analysis showed the necessity to reduce the real cluster folding potential strength by about 90%. Although, it is well known that, in order to fit the experimental cross sections for systems induced by weakly projectiles such as 6,7Li and 6He, the potential strength should be reduced by ~ 40-60 % [30-35], the reported reduction (90%) in the potential strength could infer the less probability of 6He to be treated as a cluster of two tritons. More sophisticated approaches could be preferable to derive the interaction potential based on three body treatment (4He+n+n) for 6He. Generally, the adopted potentials either Woods-Saxon or double folded CDM3Y6 potentials with and without considering the rearrangement term fairly described the considered data for 4,6,8He scattered from 208Pb at E = 22 MeV, where the extracted N r is very close to unity.
The Continuum discretized coupled channels (CDCC) were used to investigate a three-body projectile 6He (n+n+ 4He), assuming that the two neutrons are di-neutrons and thus take the shape of a two-body projectile (6He+2n). Moro et al. [40] improved this di-neutron model to account for four-body effects by using an effective di-neutron separation energy, they observed an effective binding energy of around 1.6 MeV rather than the 0.973 MeV predicted in the previous model [40-42]. To investigate the effect of couplings to the breakup channels, the (CDCC) method is used to analyze the experimental elastic scattering angular distributions for 6He+ 208Pb at E = 22 MeV. The results of the differential cross section using CDCC and other models are compared in Fig. 2. The total reaction cross section calculated by CDCC is equal 1313.4 mb, which agrees with the results of the other microscopic models.
4. Summary
The current study’s main goal is to conduct a further analysis of the interaction mechanism and peculiarities resulting from the scattering of 4,6,8He from the heavy target 208Pb at energy E = 22 MeV, above the Coulomb barrier. Analysis performed within both the derived real potential and the phenomenological WS potential. The DF potentials with CDM3Y6 effective interaction is considered with and without taking into consideration the effect of rearrangement term as well as Sao Paulo calculations. For 4,6,8He+ 208Pb nuclear system, the strength of the real double folded part is closed to unity to reproduce the data. All of the results are compared to the experimental data as well as to each other. On the other hand, due to the lower probability of 6He being treated as a cluster of two tritons, the analysis revealed the need to reduce the real cluster folding potential strength by approximately 90%. Additionally, for each theoretical approach, we provide potential parameters, cross sections, volume integrals, and chi square values. The calculated potential’s renormalization factor is maintained near unity. At all angular regions where the real part of potential plays a critical role in cross section calculations, the agreement between experimental data and calculated cross sections using folded potential is fairly good.











 nueva página del texto (beta)
nueva página del texto (beta)



