3.1. Structural properties

The full Heusler compounds crystallize in an ordered cubic structure with four interpenetrating face-centered-cubic (FCC) sublattices, which can be defined by four Wyckoff coordinates: A(0,0,0), B(0.25,0.25,0.25), C(0.5,0.5,0.5) and D(0.75,0.75,0.75). Two types of structure with different atomic ordering are present: the Cu₂MnAl structure (Fm3m space group, No. 225), also called L2₁- type, in which two X atoms occupy the A and B sites while the Y atom enters into the C site, or the Hg₂CuTi structure (F43m space group, No. 216), also called as XA-type, in which two X atoms occupy the A and C sites while the Y atom enters into the B site. The main group Z atom is always located at the D site for both types. According to the site preference rule in Heusler alloys, the two X atoms with more valence electrons occupy A and C positions and form the L2₁-type structure, and the two X atoms with less valence electron occupy A and B positions and form the XA-type structure. The two crystal structures of Pd₂PrX(X=Cl, F) are shown in Fig. 1. For L21-type structure of our compounds, the four Wyckoff sites A, B, C and D are occupied by Pd(A), Pr, Pd(C) and X(Cl, F) atoms, respectively. On the other hand, for the XA-type structure, the four Wyckoff sites A, B, C and D are occupied by Pd(A), Pd(B), Pr and X(Cl, F) atoms, respectively.

In order to find the equilibrium bulk structure of Pd₂PrX (X=Cl and F) compounds, the total energy with respect to the unit cell volume is minimized and fitted to the empirical Murnaghan equation of state [²⁹]. The Energy-Volume curves for the two compounds in the ferromagnetic (FM), anti-ferromagnetic (AFM) and non-magnetic (NM) states for Cu₂MnAl and Hg₂CuTi-type structures were plotted in Fig. 2. Accordingly, in the two compounds, the Hg₂CuTi -type structure in FM state is more stable than other structure and is introduced as the ground state structure. The equilibrium structural parameters including lattice parameter (a), bulk modulus (B), derivative of bulk modulus (B’), the cohesive energy Ec (eV), formation energy Ef (eV) and the total energy differences between AFM and FM states E=EAFM-EFM for the two compounds for Cu₂MnAl and Hg₂CuTi-type structures in the ferromagnetic (FM), anti-ferromagnetic (AFM) and non-magnetic (NM) states were listed in Table I.

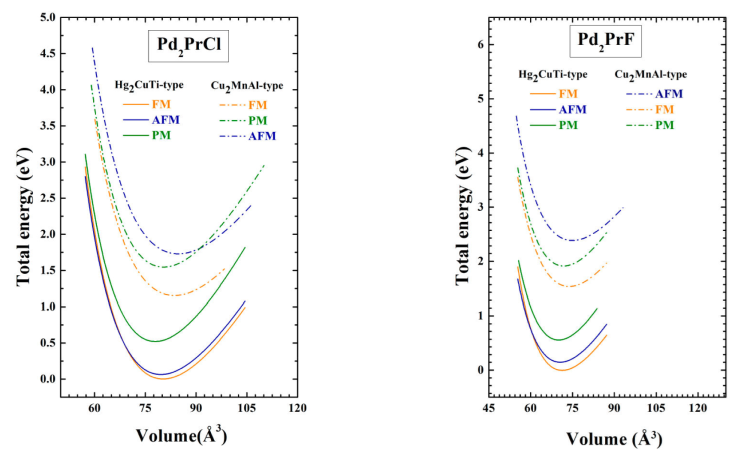
Figure 2 Total energies as functions of volume per formula unit are compared for the ferromagnetic (FM), anti-ferromagnetic (AFM) and non-magnetic (NM) states of Pd₂PrX (X=Cl, F) in the Cu₂MnAl and Hg₂CuTi-type structures, using the GGA-PBE approximation. 

The cohesive energy (E _c ) is always determined as the difference between the average energy of the atoms of a solid (particularly a crystal) and that of the free atoms for Pd₂PrX (X=Cl, F), the E _c is calculated as:

where EtotPd2PrX is the equilibrium total energy of Pd₂PrX compound, and EPd,EPr, and EX (X=Cl, F) are the total energies of the isolated atoms, the energy of an isolated atom is calculated by using a FCC lattice with lattice parameter of 20 a.u.

The negative values of E _c for Pd₂PrX (X=Cl, F) compounds show that our compounds are expected to be more stable with Cu₂MnAl structure in FM state. So, they are possible to be synthesized in the experiment.

There is no experimental or theoretical data to compare the obtained results.

EPd2PrXform represents the formation energy of the solid and this one illustrates the energy difference between a crystal and its constituents in bulk structure, which is calculated as:

where EtotPd2PrX is the equilibrium total energy of Pd₂PrX (X=Cl, F) compounds, EPdbulk, EPrbulk and EXbulk are the total energies of atomic components in bulk structure. The bulk states that adopted in our calculation of Pd is face centered cubic (f.c.c) structure, Pr is hexagonal structure, F is cubic (c) and F is orthorhombic structure. According to Table I, the negative values of formation energies indicate that these two alloys are probable to form and also are thermodynamically stable.

3.2. Elastic properties

Elastic properties of a solid are very essential seeing that they report to diverse principal solid-state characteristics such as equation of state, phonon spectra and interatomic potentials. Elastic properties are also related thermodynamically to the specific heat, thermal expansion, Debye temperature, Gruneisen parameter and melting point. So, it is necessary to determine elastic constants of solids.

Since the structure of our compounds is cubic, which need only three elastic constants in the tensor Cij, which are C ₁₁ to measure the longitudinal deformation, C ₁₂ to measure the transversal expansion and the Shear modulus C ₄₄, these constants have a primordial influence to find all the major details about the elastic, structural and mechanical properties. As shown in Table II, the values of the calculated Cij constants are positive and C12<B<C11, both the compounds satisfy the Born-Huang stability criteria [³⁰, ³²] as given in the Eq. (3).

The bulk modulus B and the shear modulus G are two reputed modules for measuring compressibility and stiffness of materials. The shear modulus G defines the resistance to plastic deformation and B determines the resistance to fracture. Using the relations (4) and (5) the values of these parameters are calculated.

where GV and GR are determined from the Eqs. (6) and (7), where V and R represent Voigt and Reuss bounds, respectively.

The bulk module B of the compounds is listed in the Table II, we see that the values of B calculated with the elastic constants are in accordance with our results found previously. Our results indicate that Pd₂PrCl and Pd₂PrF are mechanically stable.

We have also calculated Young’s modulus E which is a quantity that measures an object or substance’s resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress-strain curve in the elastic deformation region. A stiffer material will have a higher elastic modulus [³³]. The Eq. (8) [³⁴, ³⁵] determines E according to G and B.

The value of the Young’s modulus E is greater for Pd₂PrF as shown in Table II, so we can say that Pd₂PrF is the stiffer.

The Kleinman parameter ζ It describes the relative positions of cation and anion sub lattices under volume conserving strain distortions for which positions are not fixed by symmetry [³⁶] and can be expressed as:

It is current that the result of minimization of bond bending and bond stretching, respectively are ζ = 0 and ζ = 1. It is known that if the value of Kleinman parameter ζ is close to 0 the bond bending is dominated and when it closes to 1 the bond stretching is dominated. The calculated values of Kleinman parameter for our compounds are listed in Table II and the values are close to 1, thus in Pd₂PrCl and Pd₂PrF studied here the bond stretching will be dominated over bond bending.

The Lamé parameters (also called the Lamé coefficients, Lamé constants or Lamé moduli) are two material-dependent measures indicated by the first coefficient (λ) and second coefficient (μ) that arise in strain-stress relationships [³⁷], this two coefficients are always positive for most of the materials and we can calculate them by the following relations (10)

Any material is isotropic when μ=(C11-C12)/2 [³⁸], our compounds are satisfying this condition, hence they can be called as isotropic materials.

The degree of elastic anisotropy of a solid material is measured by the anisotropic ratio (A). theoretically, it defines how far a material is from being isotropic (if A = 1 the material is purely isotropic while it deviates from this value is called anisotropic material) and its mathematical definition is given by this following equation [³⁹]:

As shown in Table II, we observe that the values of A are not equal to unity, indicating the fact that our compounds are anisotropic.

Another important mechanical parameter is Cauchy pressure C _p , used to illustrate the bonding nature of compounds. If the pressure is positive the material is expected to be ductile, and in the case of a negative pressure it is brittle, the C _p is determined by the Eq. (12) [⁴⁰].

From the Table II, for our materials the value of Cp is positive, this shows that the compounds are ductile.

Pugh’s ratio B/G [⁴¹] is also the factor which attributes to describe the brittle or ductile property of compounds, if B/G > 1.75 the material is ductile, otherwise the material is brittle.

Our two materials are ductile because their B/G is larger than 1.75 which is equal to 3.11 and 2.47 for Pd₂PrCl and 2.69 and 3.10 for Pd₂PrF with GGA-PBE and GGA-PBE+U respectively.

The Poisson’s ratio v, It is defined as the ratio of transverse contraction strain to longitudinal extension strain in the direction of stretching force, is also another element which allows to defined the ductile/brittle character of a material, according to Frantsevich rule if the poisson’s ratio is smaller than 1/3 the material will be brittle or else the material will be ductile [⁴²], v is determined by the following equation.

As shown in Table II, we observe that the values of v are greater than 1/3 for Pd₂PrX with GGA-PBE and GGA-PBE+U, again confirming the above results.

3.3. Electronic properties

The self-consistent scalar relativistic band structures for the Pd₂PrX (X=Cl ,F) along the various symmetry lines within the GGA-PBE and GGA-PBE+U scheme are given in Figs. 3 and 4, there is an overall topological resemblance for the two methods. The majority spin band is metallic, while the minority spin band shows a semiconducting gap around the Fermi level, where the values are shown in Table III.

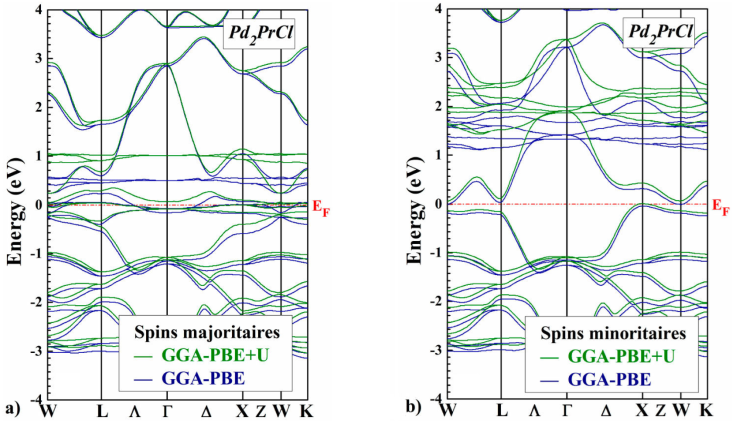
Figure 3 Comparison of GGA-PBE and GGA-PBE+U spin-polarized band structures a) spin up, and b) spin down of Pd₂PrCl for the Hg₂CuTi-type structure, calculated at the equilibrium lattice constant. The horizontal dashed line indicates the Fermi level. 

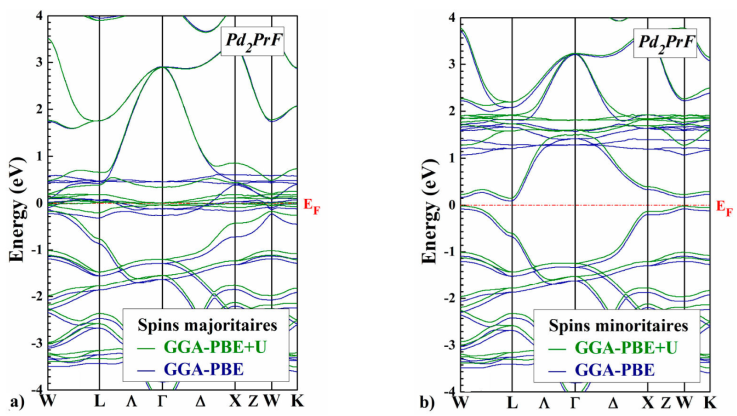
Figure 4 Comparison of GGA-PBE and GGA-PBE+U spin-polarized band structures a) spin up, and b) spin down of Pd₂PrF for the Hg₂CuTi-type structure, calculated at the equilibrium lattice constant. The horizontal dashed line indicates the Fermi level. 

The energy gap in the minority-spin band gap leads to 100% spin polarization at the Fermi level, resulting in the half-metallic behavior at equilibrium state.

The electron spin polarization (P) at the Fermi energy (E _F ) of a material is defined by the following equation:

where ρ​​↑ and ρ​​↓ are the spin up and spin down density of states at the Fermi level E _F [⁴³].

The main difference which appears between the two approaches lies in the band gap of the spin-down channels of Pd₂PrX (X=Cl, F). More precisely, with GGA-PBE+U approach, we can see that the band gap is more significant than the previous two. For the two approaches, we observe that the minimum of conduction band is situated at the (W) point and the maximum of valence band is located at (Γ) point and (W) for Pd₂PrCl and Pd₂PrF respectively, this implies that Pd₂PrCl presents an indirect band gap equal to 0.06 eV and Pd₂PrF presents a indirect band gap equal to 0.25 eV with the GGA-PBE+U.

3.4. Magnetic properties

The calculated values of the total, local magnetic moments and the contribution of interstitial regions for Pd₂PrCl and Pd₂PrF with the GGA-PBE and GGA-PBE+U methods of the Hg₂CuTi-type are listed in the Table III, the magnetic moment is exactly 2 μB per unit cell.

The calculated total magnetic moment satisfies the rule of the Slater-Pauling behavior in the full-Heusler alloys [⁴⁴]. Mtot is related to the total valence electrons (Ztot) of alloys in this rule.

In order to obtain Slater-Pauling equations for HM Pd₂PrCl and Pd₂PrF compounds, the band structures of these alloys should be considered.

The majority spin bands are occupied with 17 electrons. Thus, the number of occupied minority states (N​​​↓) is calculated as:

where N​​↓ is the number of occupied majority (spin-up) states. Therefore, Mtot is calculated as:

Pd₂PrCl and Pd₂PrF compounds have 32 valence electrons (Ztot = 32, 20 from the two Pd atoms, 5 from Pr and 7 from Cl (7 from F)), and Mtot according to Eq. (16) the Mtot is equal to 2 μB for our compounds which are in a good agreement with the results of Table III, as expected, all HM ferromagnets investigated exhibit an integer magnetic moment for the two methods. The magnetic moment is mainly localized on the Pr atom. Indeed, this atom contribute a large and positive magnetic moment, the magnetic moment on the Pd, Cl and F atoms are small.

3.5. Thermodynamic properties

The thermodynamic properties of Pd₂PrX (X=Cl, F) are determined by using the Debye model, implemented in the GIBBS code [²⁸, ⁴⁵], It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to the Einstein model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low temperature dependence of the heat capacity, which is proportional to T³- the Debye T³ law [⁴⁶].

From the calculated energy-volume points, the quasiharmonic Debye model allows one to obtain all the thermodynamics quantities, in which the nonequilibrium Gibbs function G*(V,P,T) is expressed as follows [¹⁹]:

which is a function of (V, P, T), where Esta is the static energy and EVib* is the vibrational Helmholtz free energy in nonequilibrium condition. The electronic free energy is described by Fel*. The vibrational contribution in terms of Debye model is given as

where g(ω) is the phonon DOS (phDOS) and ω is the vibrational frequencies. Other thermodynamic properties such as entropy S, heat capacity Cv, thermal expansion coefficient (α) and Grüneisen parameter (γ) are calculated from the following relations:

We employed the E - V data (total energy E and volume V) of the primitive cell as data entered into the Gibbs program. These values E and V are determined in the previous part of the structural properties in the ground state T = 0 and P = 0 as part of the approximation (PBE-GGA) using the Wien2k code. These properties are determined in the temperature range from 0 K to 1000 K for Pd₂PrCl and Pd₂PrF.

The interest of the thermodynamic properties in material science motivated us to investigate the cell volume, bulk modulus and the specific heats C _v at constant volume and pressure.

The variation of the lattice parameter as a function of the temperature at different pressures for our compounds Pd₂PrCl and Pd₂PrF respectively are represented in Fig. 5.

Figure 5 Lattice parameter versus temperature at different pressures for Pd₂PrCl and Pd₂PrF. 

We observe that the parameter (a) increases with increasing temperature at a given pressure, but reduced with increasing pressure at a given temperature. The growth rate of the lattice parameter with reduced temperature and with increase pressure, temperature can cause expansion and pressure can suppress this effect.

The calculated values of lattice parameter for Pd₂PrCl and Pd₂PrF compounds respectively at T = 300 K and P = 0 GPa are equal to 6.87 and 6.61 Å.

The Bulk Modulus is a property that defines the resistance to change of volume when compressed [⁴⁷], the compressibility module variation according to the temperature at different pressures for the two compounds Pd₂PrCl and Pd₂PrF is represented in Fig. 6, Unlike the lattice constant, the compressibility module B ₀ increases with the increase of the pressure at a given temperature, and reduced with the increase of the temperature at a given pressure.

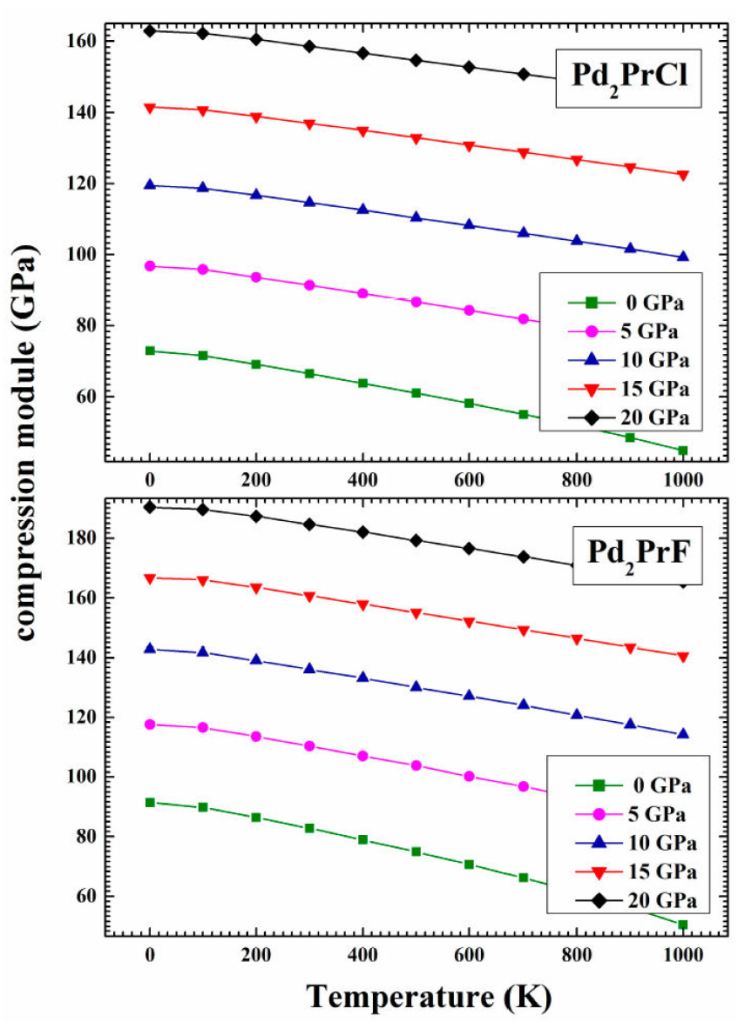
Figure 6 The compressibility module variation according to the temperature at different pressures for Pd₂PrCl and Pd₂PrF. 

The calculated values of the compressibility module for Pd₂PrCl and Pd₂PrF respectively at T = 300 K and P = 0 GPa are equal to 66.07 GPa and 82.82 GPa.

The Debye temperature θ _D is the temperature of a crystal’s highest normal mode of vibration, i.e., the highest temperature that can be achieved due to a single normal vibration [⁴⁸]. Figure 7 show the variation of the Debye temperature θ _D depending on the pressure and temperature for Pd₂PrCl and Pd₂PrF. We note that the debye temperature θ _D decreases with the increase of the temperature at a given pressure, and increases with increasing pressure to a given temperature and we can also note that θ _D is almost constant from 0 to 100 K and decreases when the temperature rises quadratically from T > 100 K, the Debye temperature values θ _D for Pd₂PrCl and Pd₂PrF respectively at T = 300 K and P = 0 GPa are equal to 271.64 and 304.49 K.

Figure 7 Debye temperature versus temperature at various pressures for Pd₂PrCl and Pd₂PrF. 

The Heat capacity C _v is an extensive property of matter, meaning that it is proportional to the size of the system. When expressing the same phenomenon as an intensive property, the heat capacity is divided by the amount of substance, mass, or volume, thus the quantity is independent of the size or extent of the sample [¹⁹].

Figure 8 represent the Variation of the heat capacity C _v versus temperature at some different pressures for Pd₂PrCl and Pd₂PrF, at Low temperature (T < 500, T < 600. k) for Pd₂PrCl and Pd₂PrF respectively, the heat capacity C _v is proportional to T ³.

Figure 8 Heat capacity C _v versus temperature at different pressures for Pd₂PrCl and Pd₂PrF. 

For high temperatures C _v is quite close to the classic limit of Petit and Dulong [⁴⁸]. Where C _v approaches approximately 99.29 and 99.30 JM^-1K^-1 for Pd₂PrCl and Pd₂PrF respectively. The calculated values of heat capacity C _v at T = 300 K and P = 0 GPa are equal to 96.03 and 94.67 JM^-1K^-1 for Pd₂PrCl and Pd₂PrF respectively.

The Entropy of system S was introduced by Rudolf Clausius, he considered transfers of energy as heat and work between bodies of matter, taking temperature into account. Bodies of radiation are also covered by the same kind of reasoning [¹⁹]. The results of calculating the entropy according to the temperature at different pressures for Pd₂PrCl and Pd₂PrF are illustrated in Fig. 9.

Figure 9 Entropy versus temperature at various pressures for Pd₂PrCl and Pd₂PrF. 

We note that the entropy increases almost linearly with the increase temperature and decreases with each given pressure value. The calculated values of entropy S for Pd₂PrCl and Pd₂PrF respectively at T = 300 K and P = 0 GPa are equal to 146.50 and 134.81 JM^-1K^-1.