1. Introduction

Recent advances in nano-fabrication technology have offered a wide range of opportunities for realizing quantum dots QD with various kind of shapes and confining potentials, which have attracted considerable attention due to their unique optical properties like broad absorption, tunable and narrow emission [¹], as well as their potential applications in electronics and optoelectronic devices, such as solar cells [², ³], lasers [⁴, ⁵], photodetectors [⁶], light emitting diodes (LEDs) [⁷] and bioimaging [⁸]. Today, multiple layered QDs are attracting widespread interest in modern materials science and technology, with far more advantages and tuning capabilities compared with a single QD material. However, is well known that the strain originates from the lattice mismatch during the growth of the quantum dots [⁹-¹²]. Under an applied stress, there will be piezoelectric charges produced, so in order to avoid such nuisance, the material’s crystal structure must be the same for all layers while the lattice constants should not differ by more than 12 % [¹³].

We use a single band description intended for one electron state in the conduction band with its minima located at the center of the first Brillouin zone Γ. This simple model was designed as an approximation if the considered semiconductor has a fairly isolated conduction band at least for a finite region in k space near the band edge. This is typically true for the conduction band of most III-V and II-VI semiconductors [¹⁴]. In order to add boundary conditions or take into account some external smooth and slowly varying perturbations, we use the well known envelope function approximation (EFA) which proved quite useful for cases similar to our own [¹⁵-¹⁷]. This model has been used for quite a long time as a reliable tool to describe many different types of nanostructures, in particular, quantum wells (QW’s), superlattices, quantum wires and nanowires, and quantum dots [¹⁸]. What makes this model easy to choose is determined by several advantages such as the overall simplicity compared to other computational tools, while including all complexities such as the periodicity of the crystal, strain [¹⁹] in addition to the effect of remote bands in the effective mass tensor. However the (EFA) method has also some limitations, as it is applicable only to nanocrystals with radii more than approximately 1 nm [²⁰], while author in [²¹] concluded that even though (EFA) is not perfectly accurate, it can be very useful from the conceptual point of view and often provides valuable physical insight.

Within the framework of the effective mass approximation (EMA), several numerical methods are employed to solve the effective mass Schrodinger equation associated with several confining potentials in a multi-layered quantum dot, such as the finite difference method [²², ²³], the finite element method [²⁴, ²⁵] the fourth-order Runge-Kutta method [²⁶], the Shooting method [²⁷] and the numerical potential morphing method (PMM) [²⁸] which was used to investigate theoretically the combination effects of the tilted electric and magnetic fields on the binding energy of an on-center donor impurity localized in a GaAs/Al_0.3Ga_0.7As cylindrical QD [²⁹, ³⁰]. These numerical methods can be quite useful downright mandatory when the targeted potential does not have a closed analytical solution, which is unfortunately the case most of the time.

A great deal of work has been done on the nonlinear optical properties of low-dimensional semiconductor quantum systems while taking into account the variation of both the geometrical and dimensional properties for potential applications in non-linear optical devices. Cylindrical quantum dots were and still a very common geometrical choice for the study of nonlinear optical phenomena in low dimensional structures [³¹-³⁴]. The study in Ref. [²] indicates that, by changing the shape of quantum dots, the performance of solar cells is slightly modified. Moreover, it has been demonstrated that the quantum dots size, and light concentration play a key role in searching the maximum efficiency of multiple quantum dot solar cells. Various results indicate that large optical nonlinearities compared to bulk materials can be enhanced due to the quantum confinement effects [³⁵]. While linear and nonlinear dielectric function have been theoretically investigated for CdS/ZnS cylindrical core/shell quantum dot embedded in PVA, PMMA and SiO₂ matrices. Results showed that the presence of the dielectric mismatch in the QD-matrix system can lead to a significant enhancement of the nonlinear dielectric function [³⁶]. On the other hand, applying an external electric field is also a powerful tool to change the electronic and optical properties of low-dimensional semiconductor structures. Ungan et al. have analyzed the effects of the external electric and the intense laser fields on optical properties in a cylindrical quantum dot with axial Morse confinement potential using the total optical absorption coefficient as well as relative refractive index changes [³⁷]. The influences of the electric fields on the systems can lead to different results depending on the confinement potential of the QDs, which can in turn modify its optical properties. Author in Ref. [³⁸] have theoretically studied the size dependent third-order nonlinear optical susceptibilities for third-harmonic generation (THG) and quadratic electro-optic effects (QEOE) of ZnS/CdSe cylindrical quantum dot quantum well (QDQW) under strong confinement. In Ref. [³⁹], it has been shown that by applying and varying external electric field, one can control the magnitude and resonance wavelength of third-order nonlinear susceptibility of GaN/AlGaN spherical quantum dot. While using the variational method, author in Ref. [⁴⁰] performed a theoretical study of the ground state binding energy and the photoionization cross section of an impurity confined in a hollow cylindrical core-shell quantum dot under the influence of the hydrostatic pressure and temperature, which reveals how much the electronic and optical properties are sensitive to variation of the pressure and temperature.

The main purpose of this paper is to explore the effects induced by the application of an electrostatic field parallel to the z axis, on both the electronic and optical properties of a fixed size cylindrical multi-layer quantum dot, while taking into account the variation of the internal layer thicknesses by considering four different layer thickness configurations. All calculations are made within the framework of the effective mass approximation, using the finite difference method to generate the required energy eigenvalues and eigenfunctions needed to calculate the transition energy, transition dipole moment and absorption coefficient.

2. Theoretical framework

Here we shall consider the motion of a conduction band electron confined inside a multi-layered cylindrical quantum dot, formed by alternating different semiconductor materials on each layer, chosen to be based of ZnS and ZnO grown along the principal axis of the quantum dot which is selected parallel to the z-direction, which result in a low dimensional system with four ZnS barriers encapsulating three parabolic ZnO wells, while making sure that first and last layer are composed of ZnS, as it have the highest conduction band edge compared to ZnO.

Figure 1 Schematic plot of a multi-layer cylindrical quantum dot grown along the z-direction. 

The Hamiltonian describing such system is given in the form suggested by BenDaniel and Duke [⁴¹] as follows:

The first term describes the kinetic energy of the confined electron in a system with a position dependent effective mass me*(z), defined as follows:

The second term V(z) encapsulates both internal and external effects that can add further restrictions to the motion of the electron. For the system in question here, it can be treated using the following form:

where V _p (z) is the internal confining potential, which create a spacial restriction created by stacking various layers with different semiconductor materials which create barriers and wells as a result of having different conduction band edge energy. The wells that are based on ZnO are described by using a parabolic potential, as shown bellow:

where V ₀ is the potential offset, defined as the difference between the conduction band edges of ZnS and ZnO, while Δ _i is the thickness of the ith layer and p _i is defined in general as p _i = (L _i + L _i-1 )/2, where L _i is defined as the sum of all layer thicknesses up to the ith layer, meaning that L ₇ equals the total height of the quantum dot. The second term defines the external potential which describes the effects of an electrostatic field with field strength noted as F, pointing opposite to the z-direction, in order to create lower potential energy spots located at the other end of the quantum dot.

This type of equation with such boundary conditions in addition to the influence of an external electrostatic field potential can be quite challenging to solve analytically if that is even possible, which leads us to rely completely on numerical methods in order to overcome this major difficulty, in this paper we apply the finite difference method (FDM).

The formula needed to compute the absorption coefficient α(ω) can be retrieved by solving the master equation defined as follows:

A two-level system is used with a transition starting from an initial state with lower energy E _i to a final state with higher energy E _f , this eigenvalues alongside their corresponding eigenfunctions can generated by solving Eq. (1), while including the viscous damping Operator Γ^. In order to solve such system, we use an iterative scheme using the Dirac picture within the electric dipole approximation on the total Hamiltonian given in the following:

where M _z is the z-axis component transition dipole moment (TDM) while E _z (t) is the AC electric field polarized also in the z-direction.

By following the standard way of solving Eq. (5), we can find the density of order (n), ρ ⁽ⁿ⁾ (ω) which is required in order to calculate the electric susceptibility of order (n), χe(n)(ω) in the frequency domain, which is expressed for the first and third order as follows:

thus we can write the total absorption coefficient in the form:

where n _r is the refractive index and c is the speed of light.

3. Results and discussion

In the numerical calculations carried out for this quantum dot, we fix both the quantum dot’s radius and height respectively to R = 5 nm and h = 10 nm, we set the reference energy at the bottom of the conduction band situated in ZnO. We take all the parameters from Ref. [²⁹]: the band offset at the interface between the two materials V ₀ = 292.8 meV, the effective mass for the electron’s conduction band m1e*=0.24m0 for ZnS and m2e*=0.265m0 for ZnO, where m ₀ is the free electron mass; the charge carrier density σ _v = 1.7 × 10²⁴ m^-3; the refractive index n _r = 2.9629; and the state lifetime τ = 1 ps. Throughout this simulation, we define firstly the representation of the electron’s state confined inside the quantum dot as (n _z , n _r , l), then we consider four distinct layer thickness configurations, starting by labeling the first configuration as the layout where all thicknesses are chosen to have equal widths, which makes each layer have thickness equal to Δ = 10/7 nm, as for all the remainders, we lower all the ZnS barrier thicknesses to Δ_1,3,5,7 = 1 nm and concentrate only on varying the ZnO layer thicknesses. With that being said we define the second configuration as Δ₂ = 8/3 nm and Δ_4,6 = 5/3 nm, then the third configuration is defined as Δ₄ = 8/3 nm and Δ_2,6 = 5/3 nm, finally the fourth configuration as Δ₆ = 8/3 nm and Δ_2,4 = 5/3 nm.

In Figs. 3 and 4 we show respectively the ground state and first excited state electron probability density within a 10 nm height multi-layered cylindrical quantum dot, for four layer thickness configurations, while varying the electric field strength starting from 0 kV/cm up to 500 kV/cm. All probability densities computed in this simulation are along the principal axis of the quantum dot chosen parallel to the z-axis, since the electron state in the xy-plane is fixed at the ground state (n _r = 1, l = 0), this plan state has a high probability density right at the center of the circular cross section, and drop significantly as we move away from it until it vanishes at the boundary of the quantum dot. Even the electric field have no effect when all its strength is pointed in the z-direction, so we are only required to concentrate the axial probability density.

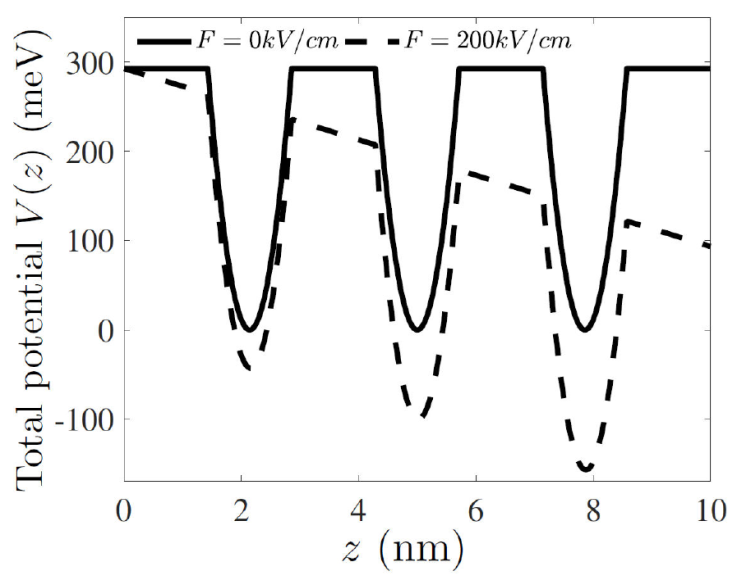
Figure 2 Plot of the confining parabolic potential with and without the effect of the external static electric field. 

Figure 3 Ground state electron probability density for different layer thickness configurations. 

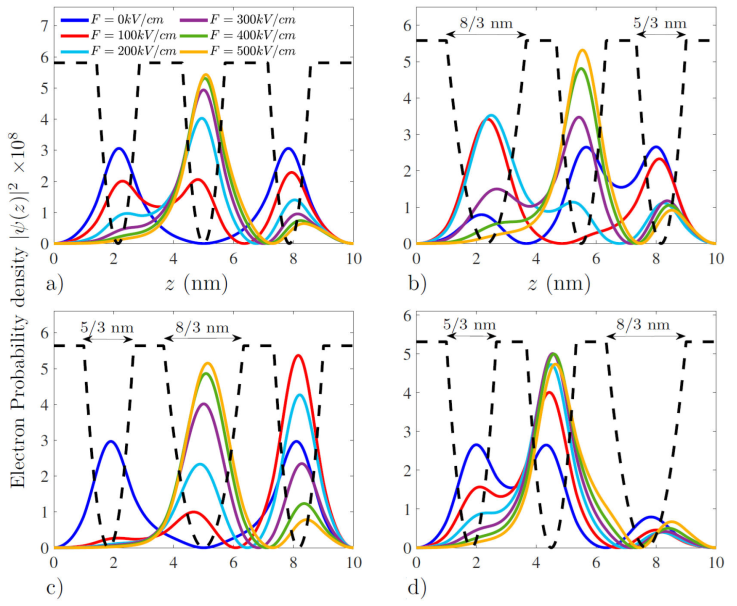
Figure 4 First excited electron state probability density for different layer thickness configurations. 

We start by looking at Fig. 3a) which gives the electron’s probability density corresponding to a layer thickness layout belonging to the first configuration. We observe at zero electric field a symmetrical distribution of the probability density across the structure, peaking up at all three ZnO wells with a general maximum value located right in the middle well, beside having a confinement energy equal to 225.22 meV. As we apply the electric field starting with a strength equal to 100 kV/cm, we observe a drop in the confinement energy to 166.31 meV in addition to a probability density shift toward the right of the structure opposite to the applied electric field direction, where newly founded states with lower energies can be occupied, while some probability density traces can be spotted in the second well. As we keep increasing the electric field strength, the electron’s confinement energy keeps decreasing accordingly until reaching -132.79 meV at a strength value of 500 kV/cm. The remaining of the probability density keeps being drained toward the third well, where the magnitude of the probability density summits. We turn next to Fig. 3b) where we treat the second configuration, where the width of the left well is superior to the rest. For the case of zero electric field, the electron starts off with a confinement energy equal to 176.4 meV, we see that the probability density is pretty much non existent anywhere except in the left ZnO well, with an insignificant value in the middle well. As we apply the electric field strength with an initial value equal to 100 kV/cm, we see a drop in the confinement energy to 139.07 meV, with a significant re-localization of the probability density out of the left well as it rearranges itself almost equally within the three ZnO well. As we further increase the electric field strength, the probability density totally changes location from the starting position corresponding to zero electric field, toward the lower energy states located at right well with a confinement energy of -159.79 meV when F is equal to 500 kV/cm. We now look at the effects of using the third configuration on the probability density as shown in Fig. 3c) which is chosen so that the middle well has the largest width compared with the others. As usual we start with the case with no electric field, we observe some similarities with the zero electric field case of the first configuration, as well as some differences such as the significantly lower confinement energy of 170.63 meV and the magnitude of the density which is more defined at the middle of the structure. As we apply an electric field strength of 100 kV/cm, no major changes were observed in the density as we saw previously, the electron experiences a big energy decrease to 118.63 meV, despite the continuing increase of the strength to 200 kV/cm the electron still retain a high probability density at the middle ZnO layer with a corresponding energy equal to 60.84 meV, however we see that the table turns when we reach 300 kV/cm as the density becomes superior at the right well with an energy around -6.35 meV, and keeps increasing as we further rise the magnitude of F, while the energy keeps dropping until reaching -159.69 meV at 500 kV/cm. Finally, while employing the fourth configuration shown in Fig. 3d), we observe that the system is just a mirror reflection of the second configuration case when there is no applied electric field, this idea can be confirmed by the fact that both cases possesses equal confinement energies of 176.4 meV, the only noticeable difference is the location of the probability density across the structure which in this case mostly settled at the right ZnO well, as it is considered a favorable position for non-zero electric field strengths, since lower energy states will be created in that neighborhood, when the electric field is applied, we see a huge energy decrease around 103.02 meV, which is the highest energy drop so far, while we observe a small shift of the probability density toward the middle of the right well, with an increase in the magnitude at the expense of both the left and middle wells, when the electric field strength reaches 500 kV/cm the confinement energy drops to -202.88 meV, which is the lowest confinement energy yet.

When considering the first excited state shown in Fig. 4a), we observe some major changes. When compared with the ground state, even though the same set of conditions are applied as before. As the electric field is absent, the probability density still remains at the low energy states located inside the ZnO wells with a confinement energy of 261.13 meV, however its divided between the left and right ZnO layers, completely ignoring the middle ZnO well, even though all layers have equal thicknesses as shown in in Fig. 4a). Then right when we apply the electric field starting with a strength of 100 kV/cm, the energy gets lowered to 211.63 meV and the probability density slowly begins to decrease at both previous ZnO wells, while filling the middle well which suffers some improvement, with a non zero probability density right within the ZnS barrier separating the left and middle well. As we keep increasing the intensity of the electric field, the electron energy keeps getting lower and the probability density magnitude keeps rising at the middle ZnO well which is apparently a more suitable for high electric field strengths, while keeping a non zero probability density in the right wells even when the electric field strength is as high as 500 kV/cm which correspond to a confinement energy of 5.9246 meV. When we consider the second configuration given in Fig. 4b) we see that unlike the ground state, the peak of the probability density is not at the largest thickness, but located with equal magnitudes within the narrow wells with a confinement energy of 219.32 meV, when we apply the electric field with strength equal to 100 kV/cm, as usual the energy decrease to 161.33 meV, and we observe a considerable increase in the probability density magnitude at the left well, while almost vanishes in the middle well, as we keep rising the strength F the probability density drops gradually form the left well and transfers to the middle well while the confinement energy keeps decreasing until reaching -31.19 meV for strength equal to 500 kV/cm. Thus we saw that the peaks keep going back and forth for field strengths bellow 300 kV/cm and settle at high electric field strength surprisingly in the middle ZnO layer just like what we saw in the first configuration. Figure 4c) shows the third case where the middle well is chosen to have the biggest thickness compared with the others. Similar behaviors with the first configuration can be seen when the electric field is absent, both cases have their peak values located in the narrow ZnO layers, while avoiding the largest well width layer, this case also has slightly lower confinement energy equal to 244.11 meV, as we apply an electric field with strength equal to 100 kV/cm, the electron’s confinement energy drops to 176.98 meV, in addition to a fast probability density transfer out of the left well, passing through the middle well where a small probability density remains there, to end up accumulating in the right well with a very high probability density peak. As we keep rising the electric field strength, the electron’s probability density ends up shifting back to the middle well once again as previously observed, while the confinement energy decrease persists as it reaches -69.0153 meV for F equal to 500 kV/cm. We conclude this section by looking at the effects of considering the fourth configuration given in Fig. 4d), which actually looks very familiar to the second configuration when the electric field is turned off as we see in Fig. 4b) with equal confinement energy of 219.32 meV. Similar thing is reported with the ground state, however there is quite a noticeable change when we apply the electric field, as the right well which presumably have the largest width, have an overall weak probability density throughout the process of varying the electric field strength. The confinement energy takes the value of 180.62 meV for strength equal to 100 kV/cm, which can be considered a bit low compared to the second configuration. Additional increase in the electric field strength obviously implies further decrease in the confinement energy until it settles down at -3.2823 meV when we reach 500 kV/cm.

Figure 5 shows the variation of the expectation value of the electrostatic electric field potential, as a function of the field strength F, first for the ground state Fig. 5a) and then for the first excited state as shown in Fig. 5b), which was computed as the energy difference between the electron state when there is no electric field and when it is present, both solutions of Eq. (1), for different layer thickness configurations, which can be computed as the following:

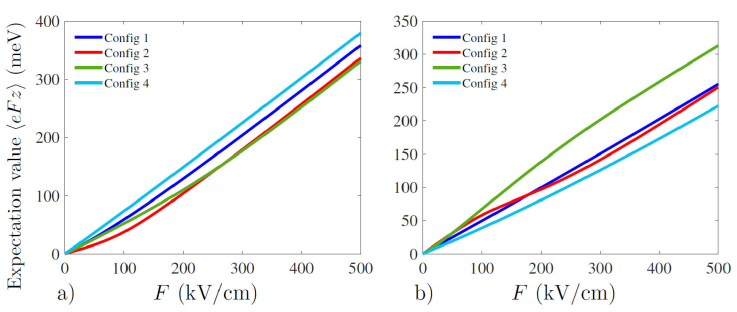
Figure 5 Expectation value of the electric field potantial as a function of the electric field strength F, a) for the ground state, b) for the first excited state. 

At first look, it might seem that this expectation value must scale linearly with the strength F, however Fig. 5 shows that it does not always have to be the case, and that can be principally due to the inner complexity of the wells modeled by the parabolic confining potential shown in Fig. 2. This expectation value which is defined similar to the binding energy, gauge the electron’s susceptibility to feel the effect of the electric field strength. As the value of the expectation value gets larger as the electron gets more vulnerable to give up energy and shift to positions with lower energies. We begin by considering the ground state shown in Fig. 5a), we see that the fourth configuration has a near linear response with a superior energy drop compared with the other cases for any given value of the electric field strength, meanwhile the second configuration started as the layout which have the lowest energy drop with a small curvature for low electric field strength below 200 kV/cm. As we further increase the strength F, the third configuration finishes by having the smallest energy drop by an insignificant difference compared with the second configuration when the strength is superior or equal to 266.33 kV/cm. Next we look at Fig. 5b) which gives the case where the first excited state is considered. We see literally the opposite of what was observed in the ground state, as the fourth configuration has this time around the lowest energy drop across all values of the electric field strength, while the second configuration started off with the highest energy drop for all electric field strength bellow 48 kV/cm. As we pass this threshold the third configuration takes its place as the highest energy drops, furthermore we observe that the second configuration gets passed once more by the first configuration starting from 178.2 kV/cm onward with a small margin which grows weaker and weaker as the strength is kept on the rise.

Now we look at the transition dipole moment briefly noted (TDM), which is a crucial parameter required for the computation of the absorption coefficient (AC), since it has a direct dependency on each electron state involved in the transition, therefore it can be altered quite easily by varying the external electrostatic field strength as we can see in Fig. 6b). The importance of this parameter lays in the knowledge offered of whether a transition can take place or not and how weak its amplitude can be compared with others, since it has to obeys strict selection rules. So in order to compute this parameter, we need to use eigenstates generated beforehand by solving Eq. (1) using the finite difference method. We see that even though the height of the cylindrical quantum dot is kept fixed, varying the inner layer thicknesses does have a visible impact on the (TDM), it can be seen by looking at the noticeable difference between the second and fourth configuration, for instance we see that all three latter configurations start off almost sharing the same value at zero electric field strength, then all deviate from one another when it is in effect, as the second configuration increases exponentially the moment we apply the electric field, peaking around 91.6 kV/cm, then rapidly decreases in a steep way as the strength value further go up, while we observe a completely different scenario with the fourth configuration as the (TDM) decreases exponentially when the strength is increased, while having the weakest (TDM) magnitude overall for all considered values of the electric field strength. We see a relatively similar behavior between the third and the second configuration, with the exception of a minuscule (TDM) decrease for strength values less than 40 kV/cm, followed by a shallow slope increase reaching a peak value shifted to a higher strength value around 226.7 kV/cm then gradually decreases as we pass that turning point. The first configuration does have some common points with the fourth one, and also stand out from all other cases as having the highest (TDM) for zero electric field strength. It can be observed that in all considered configurations the application of the electric field has mostly a negative effect on the magnitude of the (TDM) especially at high electric field strength approximately over 300 kV/cm, as all experience a reduction in the (TDM), with the exception of the second and third configuration which benefit from a magnitude boost respectively at 91.6 kV/cm and 226.7 kV/cm, which will be beneficial for the intensity of the linear and non-linear absorption coefficient peaks, assuming that this boost shall not be reduced by having a low value transition energy at the same electric field strength.

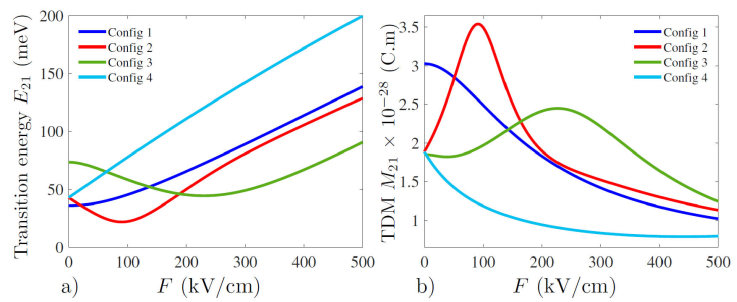
Figure 6 Transition energy a), absolute value of the transition dipole moment (TDM) b), as a function of the electrostatic electric field strength F for different layer thickness configurations. 

When we turn to the transition energy expressed as a function of the electric field strength F, it also can provide some useful pieces of information, such as the energy interval in which the peaks will vary in, and most importantly the direction and how far the peaks will shift based on the sign and magnitude of the slope at each point in the graph. Thus if the sign of the slope at a certain point is positive it will mean that the absorption coefficient will experience a blue shift while a negative sign means a red shift, then the magnitude will enable us to know how far the peaks will be displaced from one another when the electric field strength is varied by a certain amount. In Fig. 6a) we can see that the first and fourth configurations have positive slopes whatever value the electric field strength takes, which means that the peaks will only experience blue shifts, as the absorption peak start off at a low transition energy when the electric field is absent and move to higher transition energies as we increase the strength F. On the other hand the second and third configuration contain a turning point, which implies that the absorption peak will experience both red and blue shift while varying the strength F in this interval. We also observe some common traits with the transition dipole moment in Fig. 6b), like the similarity between the electric field strength corresponding to the minimum transition energy and maximum transition dipole moment for the second configuration which is in the vicinity of 90.7 kV/cm. Same thing can be seen for the third configuration where the minimum point is approximately 229.8 kV/cm which is close to the maximum point of the (TDM) shown previously, which can relatively speaking reduce the effect of the high valued (TDM) on the peak of the absorption coefficient at that electric field strength.

Figure 7 shows the variation of the absorption coefficient (AC) as a function of the incident electromagnetic radiation polarized along the z-direction with a fixed intensity of I = 10⁵ W/cm², computed for several values of the electric field strength F, while considering four different layer thickness layouts, for a fixed transition starting from a low energy state (110) toward a higher energy excited state (210). This will allow us to quantify the impact of varying both the electric field strength and the layer thicknesses on the linear and third-order nonlinear optical responses. We start by looking at Fig. 7a), which gives the linear, third order and total absorption coefficient (AC) while employing the first configuration. All Lorentzian peaks are scattered each at a specific transition energy value, as it seems that the peaks positions strongly depends on the electric field strength F. We observe that the peak corresponding to zero strength has the lowest transition energy, while having the largest optical non-linearity, however as we apply a non zero value, we observe a blue shift accompanied with a significant magnitude reduction for the third order absorption coefficient (AC). The reason why the peaks are shifting in this manner, can be explained by looking at the corresponding transition energy (blue) curve shown in Fig. 6a) which depicts the transition energy as a monotonic function. Furthermore we notice that the absorption coefficient is more pronounced for low electric field strength values, which is due to the high values that the transition dipole moment takes at low electric field strength as we see in Fig. 6b). If we then move to the second configuration, shown in Fig. 7b), we see a different peaks distribution while varying the electric field strength, as the zero valued electric field peak does not start off as the lowest transition energy as we saw beforehand, moreover having a relatively low peak magnitude with an insignificant non-linearity. When we take into account the external fields effect, we see a red shift for low electric field strength up to 100 kV/cm. We also observe a noticeable increase in the magnitude of the third order (AC) which is achieved without even increasing the incident light intensity or altering the structure of the quantum dot. The only thing of interest that was changed is the transition dipole moment and the transition energy both shown in Fig. 6, as the (TDM) summits around 91.6 kV/cm and drops that value in a steep manner until reaching 200 kV/cm, which imply that the peaks magnitude will decrease faster compared to the case where the steepness’s value is inferior. Same thing can be said about the transition energy as it reaches a minimum value around the same electric field strength which triggers a sign flip of the slope from negative to positive, which is the reason why we observe a blue shift with an important reduction in the magnitude of the absorption peak when the strength is superior or equal to 200 kV/cm. Next we look at Fig. 7c) which shows the plot of the linear, third order and total absorption coefficients depicting the case where the third configuration is used. We see that the peak corresponding to zero electric field strength starts off with a high total absorption peak with a mildly non-linearity. As we increase the strength to 100 kV/cm, we observe a red shift with a noticeable decrease in the overall peak magnitude, however we see that the third order (AC) magnitude stays approximately intact. When we reach 200 kV/cm, the peak has shifted further to lower transition energy values while we observe an increase in both the linear and nonlinear peaks. Then as we further rise the strength to 300 kV/cm we observe a blue shift, since we passed the turning point located at 229.8 kV/cm shown in Fig. 6a), which means that the slope at 300 kV/cm onward has a positive sign. On the other hand we see that the (TDM) have a slope with negative sign as we pass the turning point at 226.7 kV/cm, which will result in the reduction of the magnitude of the peaks from that point onward. We finish by looking at the case where we employ the fourth configuration Fig. 7d). We do observe some similarities with the first case which is defined as having equal layer thicknesses. Both the transition energy and dipole moment have a strictly mono-tonic behavior as shown in Fig. 6, in addition to the non-linearity which is barely visible for null or weak electric field strengths just like in the first configuration, with the exception that the transition energy steepness at electric field strengths less than 100 kV/cm is more important in this case, which results in a peak distribution with almost equal spacing throughout the variation of the strength F. Moreover there are no turning points, which will make the peaks shift solely to higher transition energies as we increase the electric field strength since the transition energy slope is always positive. However unlike all other configurations, we observe that the peaks magnitude begin to increase when we pass 300 kV/cm, which results from the almost constant value of the (TDM) in this interval as we see in Fig. 6b), while the transition energy keep increasing accordingly, as the maximum value of any absorption peak is proportional to the transition energy times the transition dipole moment squared. By looking at Fig. 7 as a whole, a conclusion can be made regarding the effects of varying both the layer thicknesses and the electric field strength, which can alter the electronic and optical properties of the quantum dot, just as the increase previously observed of the non-linearity when the electric field is applied with a strength varying bellow 200 kV/cm shown in both Fig. 7b) and c), while the opposite occurred in the remaining cases, as the non-linearity start off high valued then drops as the electric field strength is increased.

Figure 7 Total Absorption coefficient as a function of the electric field strength F, when all layers have equal thickness a), for Δ₂ = 8/3nm b), for Δ₄ = 8/3nm c), for Δ₆ = 8/3nm d). 

4. Conclusion

In this study, while using the effective mass approximation, the electronic and optical properties for a ZnO/ZnS multi-layer cylindrical quantum dot under the influence of an external static electric field has been investigated. Using the finite difference method, we have calculated the electron’s eigenvalues and eigenstates which were used to extract the probability densities and the expectation value for the electrostatic field potential for both the ground state and first excited states as a function of the electric field strength. Furthermore we computed the variation of the transition dipole moment in addition to the transition energy as a function of the electric field strength. Finally we use all the previous results to deduce the linear, third order and total absorption coefficient. All computations were done while fixing the height of the quantum dot at 10 nm but varying the internal layer thicknesses by adopting four distinct layer thickness configurations. It has been shown that varying the electric field strength alone can induce some apparent changes in the electronic and optical properties of the multi-layer quantum dot.