1. Introduction

In this work we study electron and hole transport in a semiconductor material. We wonder if an analogous effect to that of the rectification of heat flux exists in the case of particle transport in semiconductor materials. Thermal rectification is achieved when an asymmetry in the heat flow appears when the thermal boundary conditions are inverted. It has a wide range of applications which has generated great theoretical and experimental interest for many years. Thermal rectification seems to be a concomitant phenomenon of non-homogeneity, which can originate in almost any physical property of the system such as a concentration of impurities, thermal conductivity, porosity, mass density, etc. Thus, studies on thermal rectification have been carried out on systems as diverse as lattices, segmented materials, graded materials, porous media, interfaces, nanofluids, suspensions, and others. In order to address the above question we study a slightly inhomogeneosly doped Silicon layer in low injection regime and quasi-neutrality stationary condition. We assume that the particle transport in such a system can be properly described through a linear model derived within the framework of linear irreversible thermodynamics [¹-¹²]. Quasi-neutrality condition is achieved if the excess electron concentration equals the excess hole concentration across the entire sample of the semiconductor material [¹⁴]. It leads to the so called ambipolar equation which we use to obtain the stationary spatial distribution of the excess hole (electron) concentration.

Models obtained from linear irreversible thermodynamics may be applied to current transport problems which affect the transport of particles and energy in semiconductor materials. Among others, particular cases are the following. Firstly, we mention the relation of thermoelectric efficiency with the microstructure of the material. For example, the effect of bipolar transport coming from the band structure on the figure of merit [¹⁵-¹⁷]. Other examples are: the effect of local compositional inhomogeneities resulting from compaction processes on the transport properties and hence on the efficiency of the conversion [¹⁸-²⁰]. When the material is optimally doped, its thermoelectric performance can be improved. The effect of doping on both the figure of merit and the efficiency conversion may be seen in [²¹-²²]. Finally, low lattice thermal conductivity may be obtained through structural complexity on various length scales. It may be investigated microstructres like nanometer-sized inclusions among others [²³-²⁵]. This is a promising research field.

Here the ambipolar equation in quasi-neutrality regime is solved by using Wolfram Mathematica subjected to Dirichlet-Neumann boundary conditions in order to study the particle transport in a slightly non homogeneously doped Silicon layer. We obtain the stationary particle concentrations distributions for the cases defined by different boundary conditions. Our main result shows an asymmetry in the particle distribution in the case of low excess hole concentration (δp < p ₀) when the boundary conditions are reversed from Dirichlet-Neumann to Neumann-Dirichlet. The development is as follows. In Sec. 2 the ambipolar equation is obtained and the energy conservation and Poisson equations are shown. In Sec. 3 the model is simplified by considering the isothermal and quasi-neutrality conditions. We study the particle transport in a homogeneous and non-homogeneous Silicon layer in low injection regime and quasi-neutrality condition in two cases, namely, the so defined here the low level regime (LL) and the high level regime (HL). We examine the stationary state when the boundary conditions are reversed and calculate a hole flux rectification effect, which is the main result of this work. In Sec. 4 are exposed our results. We close with a discussion and conclusive remarks in Sec. 5.

2. Constitutive, transport and recombination equations

The constitutive equations for electron flux (𝐉 _n ) and hole flux (𝐉 _p ) include a term in the electrochemical potential gradient plus a contribution due to the cross effect known as the Seebeck effect in terms of the temperature gradient. According to [3], the electrochemical potential of electrons (EFn) and holes (EFp) is

respectively. In this expressions E _i is the intrinsic Fermi level, q (q > 0) is the absolute value of the elementary charge, ψ is the total electric potential, k _B is the Boltzmann constant, T is the temperature, n and p are the non-equilibrium charge concentrations and n ₀ and p ₀ are the equilibrium charge concentrations for electrons and holes respectively. So, the flow of electrons and holes are written as

here μ _n and μ _p are the electron and holes mobilities, S _n and S _p are the Seebeck coefficient for electrons and holes respectively. It is assumed that the transport properties of the material are obtained through experimental measurement.

The near equilibrium charge concentration of electrons and holes are written as follows

with

where δn and δp are the excess electron and hole concentrations, respectively. n ₀ and p ₀ are the equilibrium charge concentrations which are composed of the intrinsic charge concentration n _i and the donor N _D and acceptor N _A concentrations. The equilibrium charge concentrations satisfy

The electron and hole continuity equations are given by

where R describes the net generation and recombination of electron-hole pairs. The continuity equations above have been written to give a precise physical meaning to R [³]. Positive R means that the recombination rate overpasses the generation of electron-hole pairs while negative R means the opposite. In this investigation we consider that just the Shockley-Read Hall (SRH) generation-recombination mechanism contributes to R [²⁶, ²⁷]. It can be simplified as follows

where τ _n and τ _p are usually identified as the carrier recombination times. Here, we refer them as the recombination times. n ₁ and p ₁ are the equilibrium concentrations for electrons and holes, respectively, for the special case in which the energy level of the trap coincides with the Fermi level. In Eq. (12) it is supposed that τ _n = τ _p = τ. Moreover, the expressions for the concentrations n and p were used in the exponential form that involve the electrochemical potentials of electrons and holes.

The energy balance equation can be obtained from the principles of the linear reversible thermodynamics. It reads

where ρ and c _v are the mass density and specific heat at constant volume of the material, respectively. Note that Eq. (13) does not include lighting. The set of equations presented is closed with the Poisson equation

Here ε is the electric permittivity.

3. Quasi-neutrality and the ambipolar equation

The quasi-neutrality condition and the consequent ambipolar equation, is a frequently used model to study slightly doped materials near equilibrium. It is assumed a negligible spatial electric charge within homogeneously doped semiconductors away from junctions or boundaries, that is, the quasi-neutrality condition assumes that excess electrons concentration is balanced by an equal excess holes concentration at any point in space and time [¹³], i.e.

The quasi-neutrality condition implies ∇2ψ=0, which means that Poisson’s equation is no longer needed since it becomes decoupled from the continuity and energy balance equations. The parameter δ = (δp - δn)/δp is often used as a measure of the deviation that exists from the quasi-neutrality condition. According to [¹⁴], |δ|≪1 is an equivalent form of this condition. As it is observed in Eq. (15) we have not included a possible charge concentration in the traps as it is made in [²⁸-³¹].

Using Eqs. (3), (4), (5), (6) and (12) in (10) and (11), we can obtain the non-linear ambipolar equation for the non-isothermal case. The procedure implies multiplying by μ _p p the Eq. (10) and by μ _n n the Eq. (11). Adding these equations we get

where

In Eq. (16) the parameter D _a is called the ambipolar diffusion coefficient and μ _a the ambipolar mobility coefficient. Note that in the isothermal case the ambipolar equation reduces to

This form of the ambipolar equation is commonly found in the literature [¹⁴, ³², ³³].

The low injection condition implies that the charge carriers excess concentration δn and δp is much lower than the majority carrier concentration (n ₀ for an n-type or p ₀ for a p-type semiconductor) in thermal equilibrium. For a n-type semiconductor in low-level injection the ambipolar mobility coefficient μ _a → - μ _p and the ambipolar diffusion coefficient D _a → D _p . Similarly, for a p-type semiconductor, μ _a → - μ _n and D _a → D _n . This shows that for a doped semiconductor, the diffusion and mobility coefficient are reduced to a constant, which corresponds to that of the minority carriers for each case respectively.

The ambipolar Eq. (16), is written in terms of the charge carriers excess δp, the electric field -∇ψ and the temperature T. Using Eqs. (3) and (4) the electric field is obtained for the non-isothermal case, which in quasi-neutrality condition becomes

where J=Jn+Jp is the total electric charge flux.

The equation for the temperature is obtained from the energy balance equation. In the quasi-neutrality condition it is reduced to

In the non-isothermal case the diffusive term of the charge carriers excess ∇² δp is influenced by the temperature due to the coefficient T/T0. As expected, as the temperature T increases, there is a greater diffusion of charge carriers due to the term ∇² δp.

We finish this section by pointing out that in the quasi-neutrality condition (δn = δp) the variables of interest are the excess of charge carriers δp, the electric field -∇ψ, and the temperature T. The solutions for these variables are obtained through Eqs. (16), (19) and (20), with suitable initial and boundary conditions.

In the following section we rewrite the above equations for the particular case which is addressed in this work.

4. N-type semiconductor in quasi-neutrality condition and isothermal low injection regime

The description of electric charge and energy transport in semiconductor materials then implies the use of highly non-linear equations. In this section we discuss the equations for the isothermal case in the quasi-neutrality condition.

For the sake of clarity, in the following discussion the steady state will be considered for a n-type semiconductor (n ₀ ≈ N _D and p ₀ ≪ n ₀) and the low-injection condition (δn ≪ n ₀). Let us consider that the system can be described in one dimension and that it is subjected to Dirichlet-Neumann boundary conditions. We will also assume a negligible electric field.

The ambipolar equation then reduces to

We approximate the logarithm in the above equation to rewrite it as

with the assumption δp ≪ p ₀. Lp=(Dpτ)1/2 is known as the minority carrier hole diffusion length [³³].

Equation (22) is quite different from Eq. (21). Some differences will be here discussed and further analysis will be left to Sec. 6. Note that the low-injection condition, δp ≪ n ₀, and the quasi-neutrality condition, δp = δn, are met in both equations. However, in Eq. (22) the approximation made for the logarithm function requires that δp ≪ p ₀, while in Eq. (21) this is not necessarily required. Equation (21) is valid even if p ₀ ≪ δp. For the sake of simplicity, The case p ₀ ≪ δp will be named high level (HL) of excess carriers and the case δp ≪ p ₀ the low level (LL) of excess charge carriers. Solutions of Eq. (21) are obtained by applying the boundary conditions

where k _B is Boltzmann constant, 𝐽₀ is the value of the excess hole flux caused by the non-homogeneity of the hole concentration at the boundary x = 0 and the constant c is such that δp(1) ≪ n ₀. Equation (23) is the reduced form of the constitutive Eq. (4) (under isothermal conditions and with negligible electric field). Conditions (23) and (24) must be compatible with p ₀ ≪ δp.

On the other hand, Eq. (22) has the analytical solution

where A and B are constants determined by the boundary conditions. These conditions read

being J0' the excess hole flux caused by the non-homogeneity of the hole excess concentration at the boundary x = 0, the constant c’ should assure that δp(1) ≪ p ₀.

The non-dimensional transport equations for both of the conditions p ₀ ≪ δp, Eq. (21), and δp≪p0, Eq. (22), are obtained through the scaling

Here on, we limit the study to the one dimension case. In the previous expressions L is the length of the layer, τ ₀ a characteristic time and 𝐽₀ a typical excess flux.

If the coefficients of Eq. (21) are constants, as it is the case of a homogeneous material, the corresponding non-dimensional equation becomes

The non-homogeneous case, when the recombination time τ and the equilibrium concentration p ₀ depend on the position, the system is described by the non-dimensional version of Eq. (21). It reads

where p0*(x)=p(x)/p0 and Lp2(x)=Dpτ(x).

On the other hand, the non-dimensional version of Eq. (22) with constant coefficients takes the form

while for the non-homogeneous case we have

We continue this part by writing the non-dimensional boundary conditions of Eqs. (29) and (30) as follows

where (dp/dx) _eff is the effective slope of the excess hole spatial distribution. Similar expressions are obtained of the boundary conditions for Eqs. (31) and (32):

Here on the symbol * will be omitted in the expressions.

We now consider the slightly non-homogeneous doped semiconductor layer. In order to obtain physically meaningful expressions for the non-homogeneous recombination time and the equilibrium hole concentration, we start from the fact that in a semiconductor with indirect band gap, such as Silicon, recombination depends on the impurity concentration and that this determines the recombination time of electron-hole pairs. As a consequence, the recombination time depends on the position as well. This point will be further discussed in Sec. 6. We explore the effects of the spatial dependence of doping, by introducing a dependence of the equilibrium hole concentration p ₀ and the recombination time τ on the position. We make this by following the results of reference [³⁴] shown in Fig. 1 from their paper. Along with [³⁴] we assume that the material is crystalline Silicon with interstitial Iron. We adopt the values of N _D shown in Fig. 1 from [³⁴] for an excess hole concentration with value 10¹⁴ m^-3.

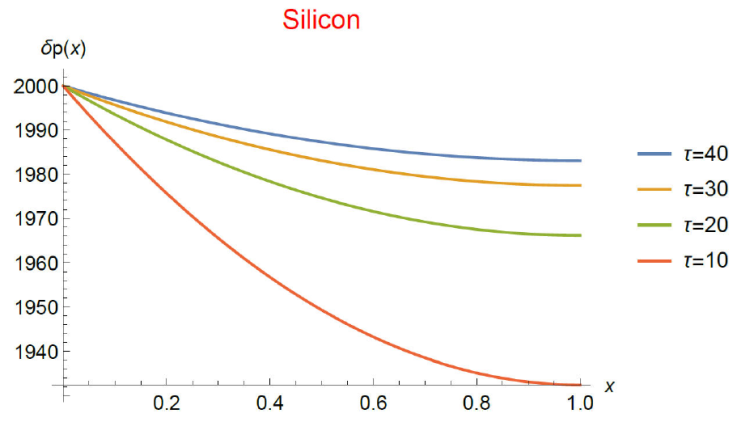
Figure 1 Stationary isothermal spatial distribution of the dimensionless excess hole concentration for a Silicon layer in low-injection regime (δp ≪ n ₀). It is obtained from numerical solution of Eq. (29) (high level (HL) condition, i.e., p ₀ ≪ δp) subjected to Dirichlet-Neumann (D-N) type boundary conditions. The recombination time is spatially homogeneous and it is measured in units of 10^-5 s. The constant 𝐽₀ in Eq. (33) has the value 10^-3 and c in Eq. (34) is 10^-2. The dimensional material length L ₀ = 10^-3 m. 

The expression we use for the spatially dependent recombination time is

with a a fitting constant and τ ₀ a recombination time fitting value, while for the doping concentration we use

being b a fitting constant and N _D0 a fitting value.

Transport equations were then solved with the specified boundary conditions. Here on, the Neumann-Dirichlet case is named N-D boundary conditions and the inverted boundary conditions, i.e. the Dirichlet-Neumann case, is named D-N boundary conditions.

Results are presented in the following section and further discussed in Sec. 6.

5. Results

For solving the transport equations we take the following values of the parameters: kB=1.38⋅10-23   JK-1, T0=300   K, μp=4.5⋅10-2   m2V-1s-1, ND0=1022   m-3. The characteristic parameters are L = 10^-3 m,

and 𝐽₀ = 1.3 · 10^-5 Am^-2. Note that the characteristic value of the flux is in other units 𝐽₀ = 1.3 · 10^-2 mAcm^-2.

The stationary spatial distribution of the excess hole concentration for different constant values of the recombination time, as derived from Eq. (29) with boundary conditions (33) and (34), is shown in Fig. 1. The same can be seen in Fig. 2 from Eq. (31) with (35) and (36).

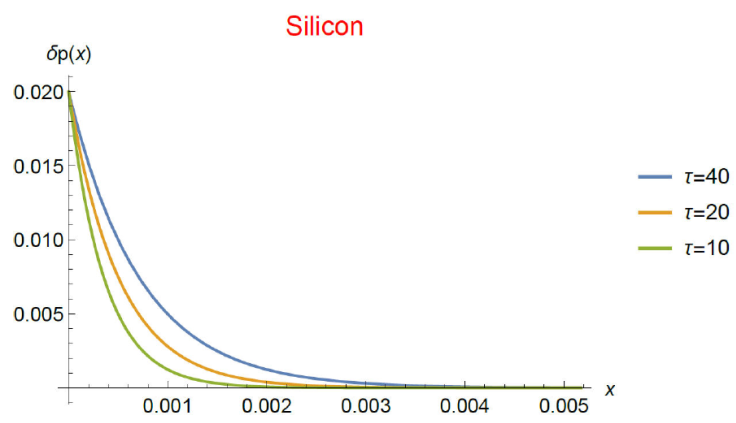
Figure 2 Stationary isothermal spatial distribution of the dimensionless excess hole concentration for a Silicon layer in low-injection regime (δp ≪ n ₀). It is obtained from the analytical solution of Eq. (31) (low level (LL) condition, i.e., δp ≪ p ₀) subjected to Dirichlet-Neumann (D-N) type boundary conditions. Position varies from 0 to 12L _p , with the diffusion length L _p = 4 · 10^-4 m. The recombination time is spatially homogeneous and it is measured in units of 10^-5 s. The constant J0' in Eq. (35) has the value 10^-3 and c’ in Eq. (36) is 2 · 10^-2. The dimensional material length L ₀ = 10^-3 m. 

The stationary spatial distribution of excess hole concentration for different constant values of the recombination time, as obtained from Eq. (29) with boundary conditions (33) and (34), is shown in Fig. 1. The same can be seen in Fig. 2 from Eq. (31) with (35) and (36). The strictly decaying behavior of the excess hole concentration observed in Fig. 2 comes from the fact that the constant B in the analytical solution Eq. (31) vanishes in all cases.

6. Discussion and concluding remarks

In summary, the low-injection particle transport regime in an isothermal Silicon film in quasi-neutrality condition was analysed. The effects of homogeneous and non-homogeneous doping on the stationary particle distributions were examined. The influence of doping was introduced in the physical model, which was derived from linear irreversible thermodynamics, Eqs (21) and (22), through the doping concentration and the electron-hole recombination time. The proposed expressions, Eqs (37) and (38) are supported by the fact that, according with the used model of particle transport, a non-homogeneous impurity concentration affects the recombination time and the equilibrium hole concentration p ₀. This last became

where we have emphasized the fact that the recombination center concentration N _D depends on position.

The influence of the non-homogeneous doping on the electric potential was left for future consideration since Poisson equation became decoupled from the continuity equations.

Firstly, we obtained the stationary charge excess concentration distribution in the low injection regime for a homogeneous material. We examined two cases, namely, when i) p ₀ ≪ δp (HL case) and ii) δp < p ₀ (LL case). The results can be seen in Figs. 1 and 2. As the figures show, the excess hole concentration in the HL case has a different behavior with respect to the concentration in the LL case. The first one has a slow decaying variation with position whereas the second one abruptly decreases in a space scale of L _dec = 5 · 10^-6m which is around 12 times the minority hole diffusion length which has a value of L _p = 4 · 10^-4m. Let us recall that the boundary condition at x = 0 is Neumann type, meaning that the system is open to particle passing. Moreover, Figs. 1 and 2 allow to make a rather obvious conclusion, namely, the bigger the recombination time the bigger the charge excess concentration. It is worth noting that the fact that the decaying length is much smaller than the diffusive length may be indicating that in the LL regime the hole transport may be of non-diffusive type.

The stationary distributions were compared when the boundary conditions (denoted b.c. here on) are inverted in the presence of doping. It is necessary to remark that the non-homogeneous spatial distribution of doping was not inverted when the boundary conditions (b.c.) did. Figure 3 shows the excess concentration distributions in the LL case for D-N b.c. (blue line) and N-D b.c. (orange line). It is observed that the distribution is asymmetric as a result of the inversion of the b.c. We mean, one is not obtained through a reflection transformation from the other. A similar result is obtained in the HL case. As it may be seen in Fig. 4, the distribution of the excess charge is clearly non-symmetric. The following considerations, which are intended to help qualitatively understand this results, are based on the fact that the only contribution to the particle flux comes from the particle concentration gradient. Let us consider then that the particle flux goes from right to left for N-D b.c, and that the flux inverts for reversed D-N b.c. According to Eq. (37), the higher values of the recombination time are located near the left hand side of the material (this distribution was maintained unchanged when the boundary conditions were inverted). This way, the particles flow from a low to a high recombination time region when the b.c. are of the D-N type and vice versa. In other words, particles move towards a region of higher recombination rate in the boundary conditions of the D-N type. In the N-D b.c. case, the situation is reversed, i.e., particles move towards a region with a low recombination rate. The charge excess concentration in the HL regime seems to be affected less by the inversion of the b.c. than the LL case. We state our main conclusion, namely, that non-homogeneity doping results in a symmetry breaking of the particle distribution of excess electric charge concentration in steady state when the boundary conditions are reversed. The fact that the particle flux is mainly maintained by the particle concentration gradient allows us to glimpse that an asymmetric particle flow is also present.

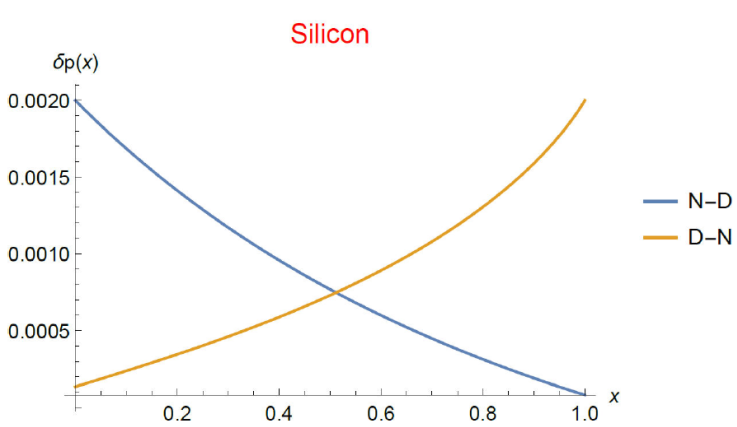
Figure 3 Stationary isothermal spatial distribution of the dimensionless excess hole concentration for a Silicon layer in low-injection regime (δp ≪ n ₀). It is obtained from numerical solution of Eq. (32) (low level (LL) condition, i.e., δp ≪ p ₀) subjected to Dirichlet-Neumann (D-N) type boundary conditions (blue) and Neumann-Dirichlet (N-D) boundary conditions (orange). The constant J0' in Eq. (35) has the value 10^-3 and c’ in i.e.(36) is 2 · 10^-2. The recombination time is taken τ ₀ = 4 · 10^-4 s. The dimensional material length L ₀ = 10^-3 m. 

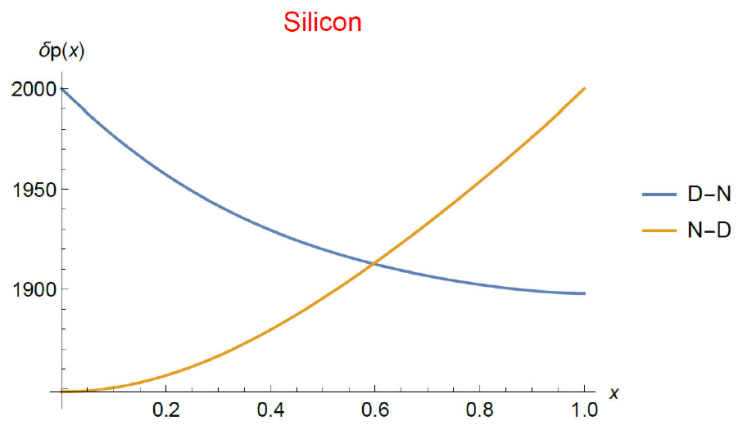
Figure 4 Stationary isothermal spatial distribution of the dimensionless excess hole concentration for a Silicon layer in low-injection regime (δp ≪ n ₀). It is obtained from numerical solution of Eq. (30) (high level (HL) condition, i.e., p ₀ ≪ δp) subjected to N-D boundary conditions (blue) and D-N boundary conditions (orange). The recombination time and the doping concentration are spatially non-homogeneous. The constant 𝐽₀ in Eq. (33) has the value 10^-3 and c in Eq. (34) is 10^-2. The recombination time is taken τ ₀ = 4 · 10^-4 s. The dimensional material length L ₀ = 10^-3 m. 

The last comment was analysed by calculating a rectification factor r defined in terms of the charge excess fluxes at the boundaries of the material. This factor is defined as

The superscript N-D (D-N) indicates the kind of b.c. used to calculate the corresponding excess flux. Note that this is made at the material extreme which is subjected to Dirichlet type b.c. condition. We obtain two different values of r in the non-homogeneous LL and HL regimes. We have

and

The above values were both obtained by taking a = 3, τ ₀ = 4 · 10^-4 s and 𝐽₀ = 1.3 · 10^-1 Am^-2.

Our conclusions may be summarized as follows: a) the excess electric charge flux in a slightly non-homogeneously doped semiconductor is asymmetric when the boundary conditions are inverted, b) the flux rectification is around 0.35 in the LL regime (δp < p ₀) while in the HL regime (p ₀ < δp) rectification does not in fact exists.

Finally, our general conclusion: particle flux rectification seems to be featuring the particle transport in slightly non-homogeneously doped semiconductor when the excess hole concentration is smaller than the equilibrium hole concentration.

A less restrictive physical situation than the one considered in this work, in which the fields of temperature and self-consistent electric potential will couple to the continuity equations, will be studied in the future.