1 Introduction

The amount of information and data generated from computer equipment, data storage clouds and cell phones continues to increase rapidly and has generated traffic jam in communications. Among the trends in optical interconnect technologies ^[1], an important part of improving communications is to use a hybrid technology, based on electronics and photonics, in a CMOS-type silicon microdevice to realize microscale optical communication functions and increase the operating bandwidth of devices ^[2]. The basic functions required by hybrid devices, e.g., coupling, modulation, and detection of an optical communication signal can be realized by narrow waveguides, ring resonators ^[3], and fiber-to-waveguide grating couplers ^[4,5,6]. A grating coupler is a periodic structure that allows coupling of a fiber to a waveguide and viceversa, being an important issue in integrated photonics microdevices.

The use of fiber-to-waveguide coupling gratings is necessary due to the discrepancy in dimensions of the intensity distribution of the fiber optic propagation mode to the waveguide propagation mode, there is an order of magnitude between them and hence low coupling efficiency ^[7]. In addition, diffraction grating coupling has better alignment tolerance and is compatible with silicon technology. Another important achievement proposes a bidirectional grating for vertical coupling. Such an improvement was achieved by using a Si₃N₄ layer on the grating, which decreases the reflected power to the fiber and increases coupling to the guide ^[8]. An interesting strategy, which has allowed the improvement in the efficiency of grating couplers, has been the use of grating period apodization and fill factor (FF), together with the optimization of the etch depth of the grating coupler and presented the best performance for SOI structures without the use of any self-reflector ^[9,10].

The development of coupling gratings ranges from communications to biodetection ^[11,12,13], but their implementation particularly in the integration of photonic functions has major limitations, and this is due to the use of Si-based nanotechnology that operates at optical communications wavelengths from 1330 nm to 1550 nm. There are several applications that operate at shorter wavelengths and this prevents them from being manufactured, due to the absorption of Si. This requires the use of materials, for example Si₃N₄ ^[14,15], Ti₂O ^[16], Al₂O₃ ^[17], among others, that allow the realization of devices of smaller waveguides, which operate in a wider spectral range e.g. 200 nm to 2000 nm ^[18,19,20].

The aim of this paper is to explore the possibility of realizing integrated optics components by means of an Al₂O₃ atomic layer deposition process (ALD) ^[21,22]. The synthesis of submicron optical waveguides and design of ring resonators by means of Al₂O₃ atomic layer deposition technique has been performed ^[23]. Therefore, the design of grating couplers with etched grooves at the same height as the submicron waveguide, is presented in this paper, which allows the fabrication of a single etching step ^[24]. The gratings analyzed are of binary and sinusoidal type for visible (633 nm) and NIR (1550 nm) wavelengths. The coupling efficiency was analyzed using the finite element method (FEM). It was calculated as a function of the main physical parameters of the grating: waveguide thickness, period, etching depth and beam incidence angle ^[25].

The rest of this paper is organized as follows. The operational concept of the gratings is presented in Sec. 2 The simulation and results of this work are shown in Sec. 3 Finally, our conclusions are summarized in Sec. 4.

2 Operating principle

A grating coupler is a periodic structure located on a waveguide to couple/decouple light towards a waveguide circuit by means of an optical fiber placed on the coupling grating ^[26]. In general, the grating coupler generates a radiation pattern that can be coupled to the fundamental mode of the waveguide; this is because one of the diffraction orders of the grating fulfills the coupling conditions since its propagation constant reaches the same value of the effective refractive index of the propagation mode of the waveguide ^[27,28]. Thus, in order for a grating coupler to allow the input-output of light from a waveguide it must satisfy the following Bragg condition:

where βc, βω are the propagation constants in the environment and waveguide, respectively; nc, nω, ns, are the refractive indices of the environment, waveguide and substrate; Λ is the spatial period of the grating, m is the diffraction order, see Fig. 1.

Figure 1 Structure of a grid coupler and decoupler. 

The waveguide propagation constant is determined by:

where neff is the effective refractive index of the waveguide propagation mode.

Equation (1) determines the entrance and exit angles of the light entering and leaving the structure as a function of the effective refractive index and the diffraction mode order. This relationship is also the basis of biosensors based on grating couplers and is given by:

Figure 2 shows the two study configurations, which is the binary grating coupler Fig. 2a) and the sinusoidal grating coupler Fig. 2b), for each configuration, the second grating is identical, presenting the same parameters (thickness of guide H, etching depth h, period Λ) as the first grating. The etching depth of the grating h forms the etched part LE and the non-etched part LO. The grating period Λ, which corresponds to the length of a scattering element, is expressed as follows:

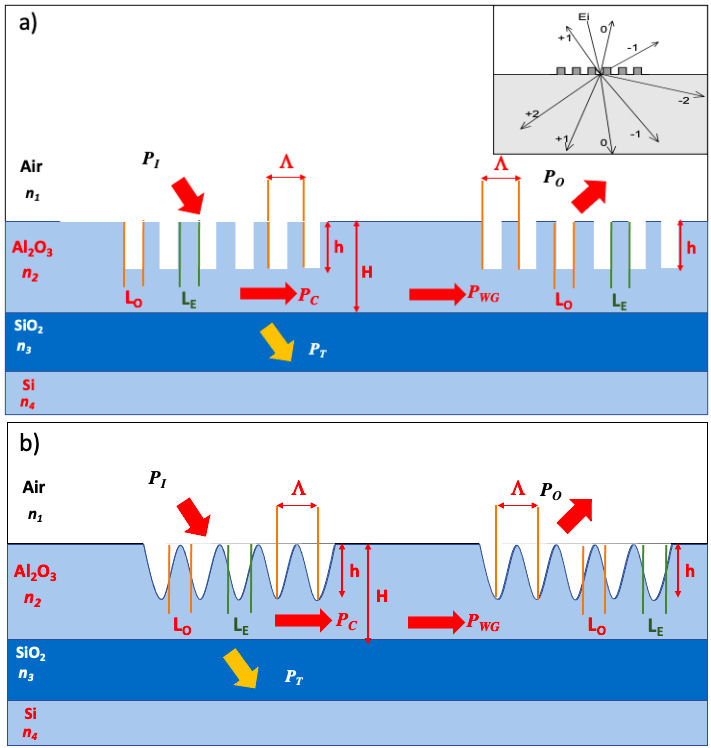
Figure 2 Schematic diagram of the geometry of a fiber-to-grating coupling. a) Binary grating, and b) Sinusoidal grating. 

The grid fill factor (FF) indicates the ratio between LO and the grid period Λ:

The first order effective refractive index of the grating is determined by the effective index of the etched section (nE) and the non-etched section (nO):

The ratio between coupled PC and incident PI powers determines the coupling efficiency ηC^[29]. And the power PT is the power that leaks to the substrate, as shown in Fig. 2.

while the decoupling efficiency ηd is calculated with the coupling power from waveguide PWG and the decoupling power PO.

The overall efficiency of the optoelectronic device is:

In general the coupling efficiency is defined as the coupled optical power from the waveguide mode to the fiber mode (or vice versa), and is mainly determined by the grating directivity, the reflected power from the grating to the waveguide, and the overlap between the radiated mode and the fiber mode ^[30]. The mechanism of how the gratings interact to redirect incident light in diffractive orders is described next. The k-mode vector of the waveguide and the variation in grating period are located toward the x-axis.

3 Simulation

It is essential to consider a starting point for the design of grating couplers; in this work, once the physical parameters of the waveguide structure are defined, the design of the grating coupler is initiated by evaluating the dependence of the grating period on the angle of incidence. With the selected values of the grating period and the angle of incidence, the variation of the grating depth for coupling efficiency is evaluated. Upon finding an observed optimum parameter, the value is fixed, and the next parameter is varied, and so on, as shown in Fig. 3.

Figure 3 Diagram for optimizing the coupling of a guide-fiber through a diffraction grating. 

After finding the maximum coupling efficiency of the first grating, the maximum efficiency of the second grating is calculated, varying only the parameters of the grating period and the grating height.

3.1 Physical parameters

TE polarization was chosen for these simulations since most SOI devices are designed to work in this mode ^[8]. In this work, the physical parameters are optimized by taking measurements of the electric field below the first grating (P1), in the middle of the two gratings (P2) and above the second grating (P3) shown in Fig. 4, with which the optimal cou-pling and decoupling efficiency conditions are obtained. The optical interconnect in Fig. 4, consists of two gratings etched on Al₂O₃/SiO₂/Si waveguide; the first grating is the coupling grating, and the second one corresponds to the decoupling. The efficiency analysis was performed for two wavelengths λ of 1.55 μm and 0.633 μm, and two types of coupling gratings, the binary and sinusoidal grating. For each of the above configurations: wavelength, and grating type, a variation of the guide thickness was performed from 800 to 1000 nm for operation 1550 nm, and from 300 to 500 nm for operation 633 nm, for the binary and sinusoidal grating, respectively, and from the simulation, the optimum thickness that showed the best coupling was determined. The FF factor in the binary grid was always close to 0.5, while in the case of the sinusoidal grid the FF factor is 0.5, because it has a sinusoidal shape.

Figure 4 Points of analysis of the electric field. 

3.1.1 Efficiency analysis at 1550 nm

A first analysis to determine the period of the coupling grating is to choose a coupling angle. In this paper, we choose a fiber optic beam initiation angle from the solution to Eq. (1), as shown in Fig. 5.

Figure 5 Variation of the period with respect to the angle of incidence for a H = 900 nm waveguide. 

The simulation was carried out with the starting parameters shown in Table I.

Table I Initial parameters of the coupling grating. 

Parameters	Initial Value
Wavelength λ (μm)	1.55
Refractive index Al2O3 (n2)	1.74
Refractive index SiO2 (n3)	1.444
Refractive index Si (n4)	3.4467
Thickness of guide H (nm)	900

According to Fig. 5, for an incidence angle of 30^o, it corresponds to a period of Λ=1400 nm. The effect of the electric field with respect to the variation of the period of the first grating at points P1 and P2 , is shown in Fig. 6a). At a wavelength of 1550 nm, in the binary coupling grating, the maximum electric field is at a period of 1570 nm, in the case of the sinusoidal grating the maximum electric field is at a period of 1705 nm. In Fig. 6b), the analysis of the electric field vs. etch depth for positions P1 and P2 is shown. In the binary grating, the maximum field is at an etch depth of h = 425 nm, with the sinusoidal grating the maximum electric field is at h = 550 nm. Next, the analysis of the electric field variation vs. the angle of incidence was performed at positions P1 and P2, Fig. 4. From Fig. 6c), it is observed that the optimal angles for the first binary grating is 30 and for the first sinusoidal grating is 31. The optimal parameters obtained are: for the binary grating a period of 1570 nm, an etch depth of 425 nm, and an incidence angle of 30^o; for the sinusoidal grating a period of 1705 nm, an etch depth of 550 nm, and an incidence angle of 31^o. The coupling efficiency of the first grating was determined considering the input power of the Gaussian beam in Fig. 7, and the power of the light propagation inside the waveguide, at the position shown in Fig. 8. The power flow analized through cross section of the waveguide is found in Figs. 8b) and 8c), whose field distribution is shown in Fig. 11.

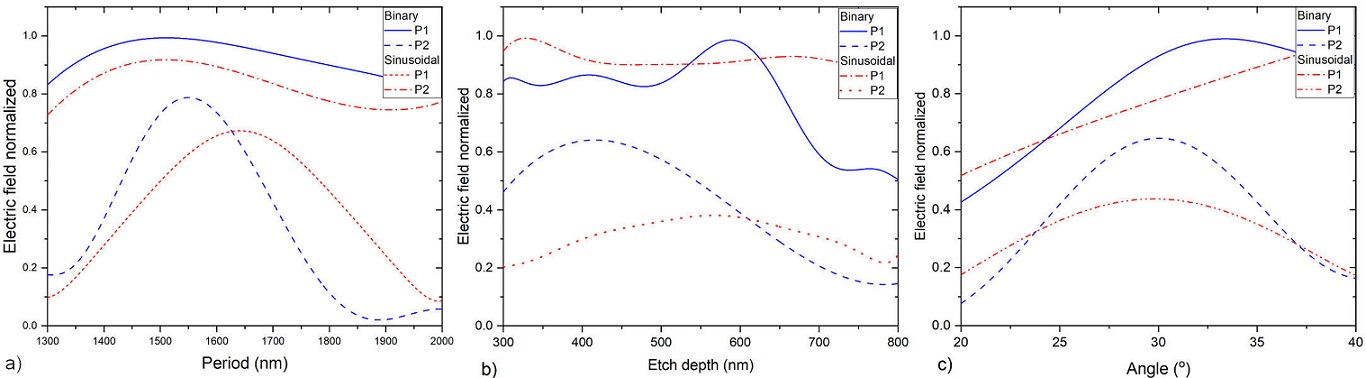
Figure 6 Electric field normalized vs. physical parameters of the coupling grating. a) Period, in both grids Λ=1570 nm, b) Etch depth, in binary grid h = 425 nm and in sinusoidal grid h = 550 nm, and c) Incident beam angle, in binary grid θ = 30^o and in sinusoidal grid θ = 31^o. 

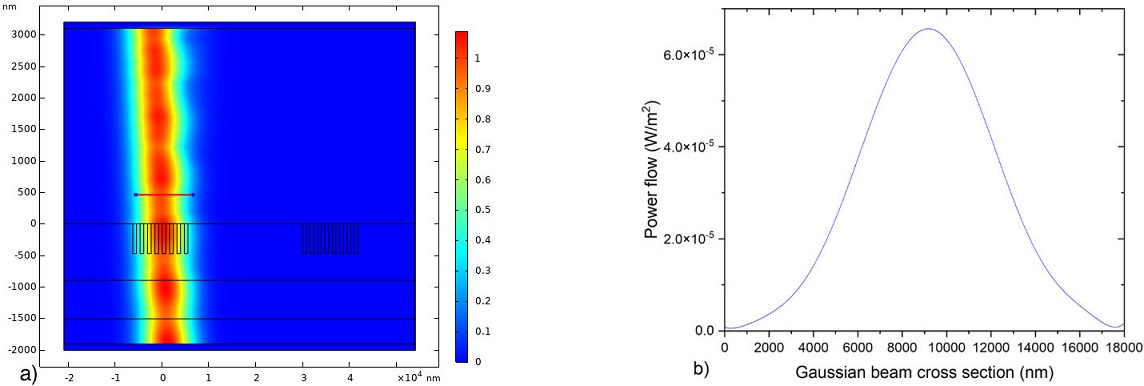
Figure 7 Simulation of the Gaussian beam with incidence angle θ = 30^o and line where the incident power flux was calculated.a) Gaussian beam, and b) Incident power profile. 

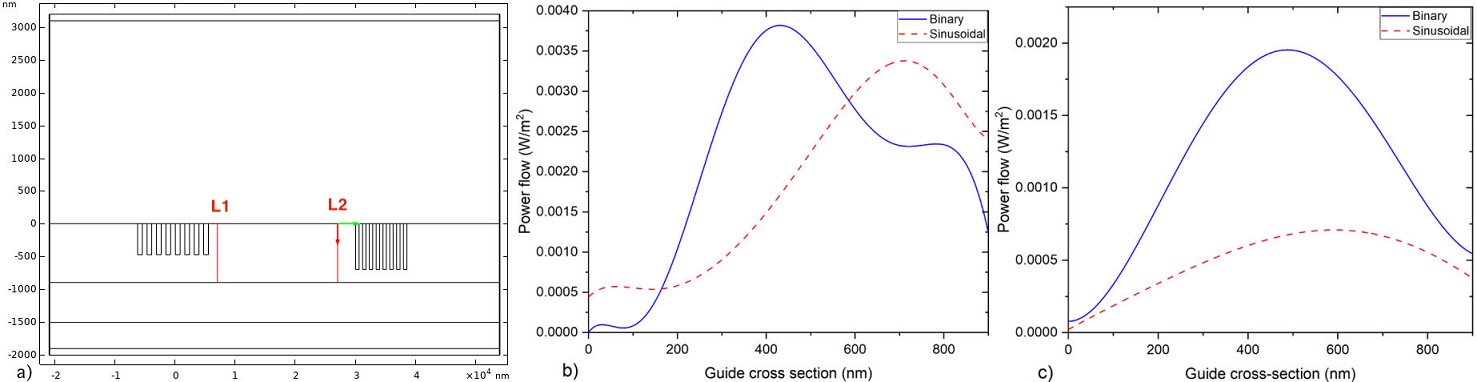
Figure 8 Power profiles. a) Lines L1 and L2 are cross section of the waveguide, b) Power distribution L1, and c) Power distribution L2. 

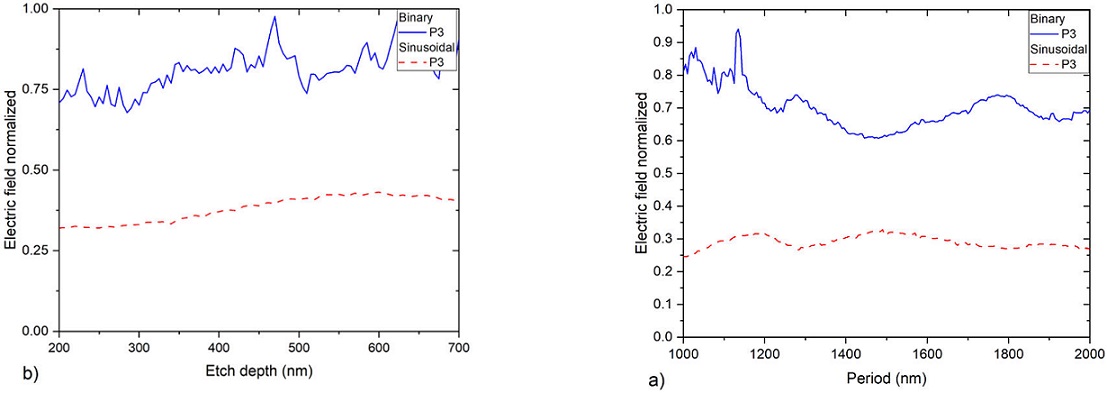
Figure 9 Electric field vs. physical parameters of the decoupling grating. a) Period, in binary grid Λ=1135 nm, and in sinusoidal grid Λ=1190 nm, and b) Etch depth, in binary grid h = 475 nm, and in sinusoidal grid h = 600 nm. 

Figure 10 Decoupling power. a) Power calculation position, and b) Power flow. 

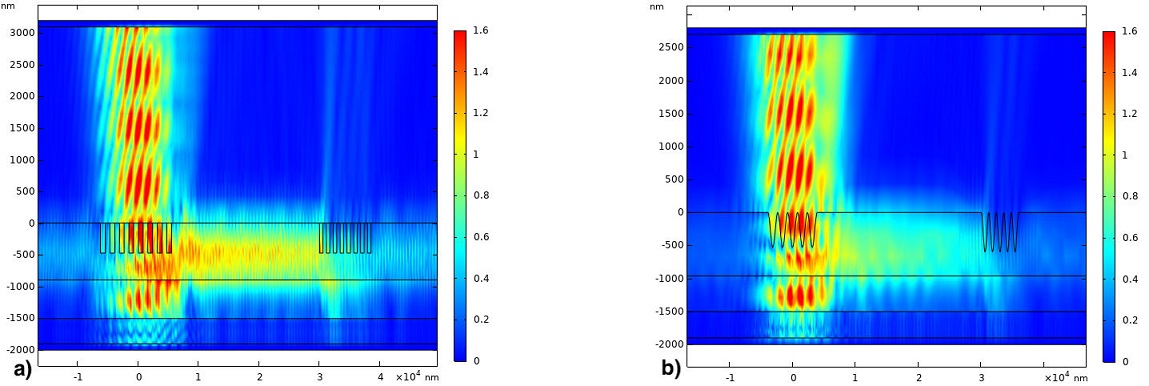
Figure 11 Intensity distribution coupling and the decoupling for a waveguide of 900 nm and λ = 1550 nm. a) Binary grating, and b) Sinusoidal grating. 

Integrating the power plots, a coupling efficiency ηC is calculated with Eq. (7), with respect to the input power PI Fig. 7 and the power in the guide PC, line L2 Fig. 8b), whose value in the first binary grating is 21% and in the first sinusoidal grating is 15%.

The maximum efficiency of the second grating was determined by varying only two physical parameters, the period and the etching depth of the grating with respect to the electric field at point P3, Fig. 9. The optimum period for decoupling according to Fig. 9a) is 1135 nm and 1190 nm, the etching depth is 475 nm and 600 nm, Fig. 9b), for the binary and sinusoidal grating, respectively. The efficiency of the second grating ηd was obtained from the power of the beam that traveled through the waveguide PWG, line L2 Fig. 8c), and the power of the decoupled beam PO, Fig. 10b). In this figure, a strong peak can be observed at the left end, the output power is unevenly distributed in the second grating, which corresponds to the expected behavior of a decoupling grating ^[9,31]. The efficiency of the second grating is 25% and 22%, for the binary and sinusoidal grating, respectively.

In Fig. 11, the simulations with the optimal coupling parameters for the case of each coupling grating are shown.

3.1.2 Efficiency analysis at λ = 633 nm

To analyze the two coupling and decoupling gratings operating at 633 nm, binary and sinusoidal, a similar procedure as above was performed. First, from Fig. 12, the period for an angle of 30^o, Λ=705 nm, was determined. In addition, the starting parameters are in Table II.

Figure 12 Variation of period concerning the angle of incidence for a H = 350 nm waveguide. 

Table II Initial parameters of the coupling grating. 

Parameters	Initial Values
Wavelength λ (μm)	0.633
Refractive index Al2O3 (n2)	1.64
Refractive index SiO2 (n3)	1.457
Refractive index Si (n4)	3.8736
Thickness of guide H (nm)	350

Figure 13a) shows the variation of the electric field vs. period. The maximum electric field is found at a period of Λ=705 nm, both for the binary grating and the sinusoidal grating. Analyzing the effect of the etching depth of the coupling grating Fig. 13b), it is observed that the optimum depth for a binary and sinusoidal grating is h = 140 nm for both. The optimal incidence angle is observed in Fig. 13c), for a binary grating θ = 30^o and for the sinusoidal grating θ = 33.5^o..The optimal parameters obtained are: for the binary grating a period of 705 nm, an etch depth of 140 nm, and an incidence angle of 30^o; for the sinusoidal grating a period of 705 nm, an etch depth of 140 nm, and an incidence angle of 33.5. From the power flux in the guide Fig. 14a), calculated at the cross section of the guide, line L1 Fig. 8a), whose field distribution can be seen in Fig. 17, the coupling efficiency ηC is 7.8% and 7.6%, for the binary and sinusoidal grating, respectively.

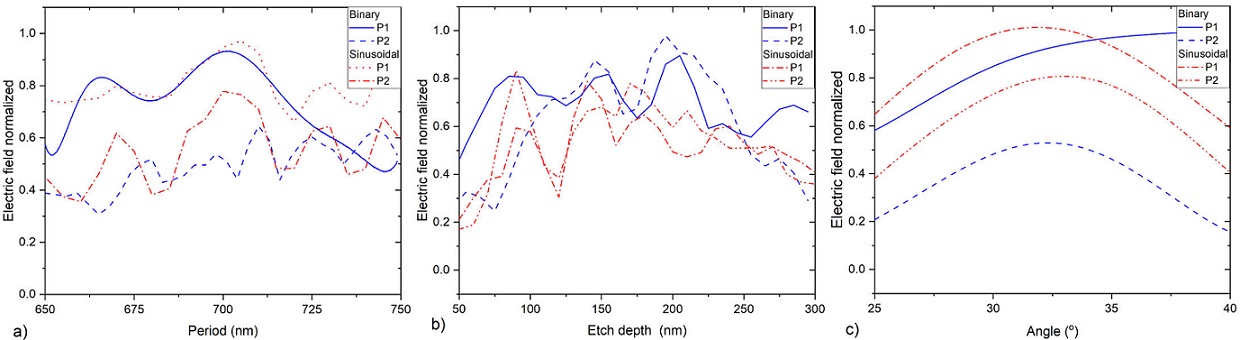
Figure 13 Electric field normalized vs. physical parameters of the coupling grating. a) Period, in both grids Λ=705 nm, b) Etch depth, in both grids h = 140 nm, and c) Incident beam angle, in binary grid θ = 30^o and in sinusoidal grid θ = 33.5^o. 

Figure 14 Power profiles. a) Line power L1, and b) Line power L2. 

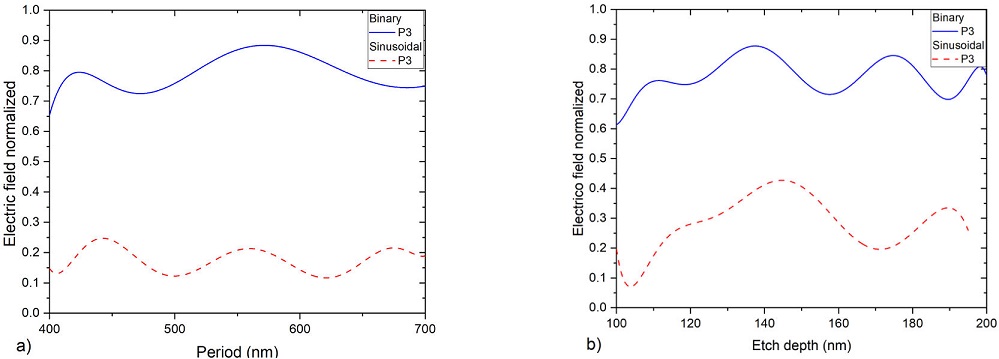
Figure 15 Electric field vs. physical parameters of the decoupling grating. a) Period, in binary grid Λ=590 nm, and in sinusoidal grid Λ=450 nm, b) Etch depth, in both grids h = 140 nm. 

Figure 16 Uncoupling power flow. 

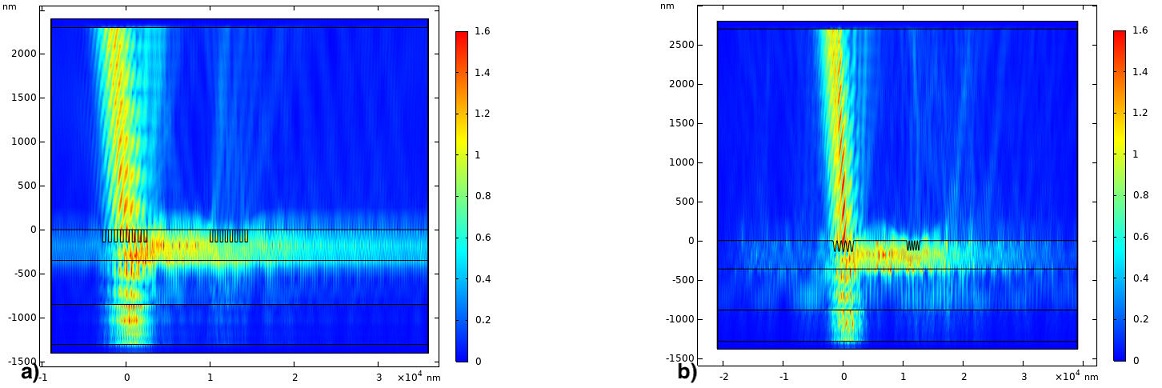
Figure 17 Intensity distribution coupling and the coupling for a waveguide of 350 nm and λ = 633 nm. a) Binary grating, and b) Sinusoidal grating. 

The calculation of the decoupling efficiency of the second grating was performed with a procedure similar to the previous one. The optimum decoupling period obtained from Fig. 15a) is 590 nm and 450 nm for the second binary and sinusoidal grating, respectively; the optimum etch depth, Fig. 15b), is 140 nm for both decoupling gratings, calculated at point P3. The decoupling efficiency ηd of the second grating was determined from the power flow in the guide PWG, line L2 Fig. 8a), whose profile is shown in Fig. 16 for both gratings. The decoupling efficiency of the second grating ηd is 25% and 22%, for the binary and sinusoidal grating, respectively. According to Figs. 9b) and 17, the decoupling efficiency of the second grating ηd is 53% and 34%, for the binary and sinusoidal grating, respectively. Figure 17 shows the simulation of the optical system with the optimal coupling and outcoupling parameters for the binary grating Fig. 17a) and the sinusoidal grating Fig. 17b).

Finally, the overall efficiency of the optoelectronic device ηT is calculated with Eq. (9), at a wavelength of 1550 nm, the efficiency is 3.3% and 1%, for the binary and sinusoidal configuration, respectively. While for a wavelength of 633 nm, the efficiency is 2.3% and 1.5%, for the binary and sinusoidal configuration, respectively. The efficiency of the coupling gratings achieved for both wavelengths is adequate and far superior to the typical efficiency with a direct fiber optic to waveguide coupling due to the discrepancy in core sizes of the two components.

4 Conclusions

In this paper, the light propagation in an optical coupler and decoupler of optical waveguides based on binary and sinusoidal diffraction gratings using the finite element method was analyzed. The results indicated coupling efficiencies of 21% and 15%, decoupling efficiencies of 25% and 22% at a wavelength of 1550 nm, coupling efficiencies of 7.8% and 7.6%, and decoupling efficiencies of 53% and 34% for a wavelength of 633 nm, can be obtained for binary and sinusoidal gratings, respectively. The optimal physical parameters of the binary and sinusoidal coupling gratings for 1550 nm were a coupling period of 1570 nm and 1705 nm, etching depth of 425 nm and 550 nm, coupling angles of 30^o and 31^o, of the decoupling gratings are periods of 1135 nm and 1190 nm, etching depth of 475 nm and 600 nm, for a thickness guide of 900 nm. Likewise, for operation at a wavelength of 633 nm, the optimum parameters achieved a coupling period of 705 nm, etch depth of 140 nm, coupling angles of 30^o and 33.5^o, and the decoupling parameters of the second grating are 590 nm and 450 nm, and etch depth of 140 nm for both gratings, for a waveguide thickness of 350 nm. These results show the feasibility of developing this type of components by optical microlithography techniques. However, there is a technological challenge that the must be taken into consideration the design parameters of the coupling gratings, their efficiency, and the coupling angle with the typical dimensions of components to be reproduced by an optical lithography, laser lithography, and X-ray lithography manufacturing process, among others.