1. Introduction
The performance of any mechanical component depends on mechanical properties of the material such as the Young’s modulus, Poisson’s ratio, strength, yielding stress, tearing stress, etc. Usually, the assessment of the performance of mechanical components is made by considering these mechanical properties, which are generally considered as constant and non-dependent on stress, temperature and time [1]. However, all the materials are actually time- and temperature-dependents. The only difference is that in some of them this dependence is more evident than in others. Polymers, and more particularly elastomers, exhibit stress, temperature, and time dependent behavior, even at the minimum variation [2]. Thus, they should be studied as viscoelastic materials. Elastomers are used as mechanical elements in several applications due to their good compliances, high friction coefficient, good sealing performance, high impact energy absorption, etc., [3]. In many applications, these materials work under severe conditions of stress and temperature, which compromise their service life and performance. On the other hand, in many applications these materials work under constant stress or constant deformation during long periods. In such conditions, creep or stress relaxation behavior of elastomers become critical [4,5]. Clearly, each elastomer has its own viscoelastic behavior for each specific stress and temperature condition, so they should be characterized under the particular conditions of the application. However, it is known that in the linear viscoelastic regime, a viscoelastic material can be characterized in term of its elastic and viscous parameters. The viscoelasticity of these materials is rarely considered in the design of engineering components or in stress/strain analysis, due to the complexity for its characterization and simulation. For example, in Ref. [6], the authors conducted creep tests to determine the creep compliance and the viscoelastic Poisson’s ratio and evaluate the effect of these mechanical properties on the stress distribution in the packaging process. Also, the linear viscoelasticity principle (although not using the viscoelastic Poisson’s ratio) was considered in the semi-analytical evaluation of the creep deformation of asphalt in the research work presented in Ref. [7]. On the other hand, due to the complexity for obtaining these properties and their inclusion in simulation models, viscoelastic properties are not commonly taken into account in the evaluation of the sealing performance of elastomers [8], neither in the prediction of multiaxial mechanical behavior of polymers [9] nor in the stress-strain analysis of biomechanical artificial replacement [10]. Thus, this work aims to characterize and compare the creep behavior of five engineering elastomers (Ethylene-Propylene-Diene Monomer, Flouroelastomer (Vitonr), nitrile butadiene rubber, silicon rubber and neoprene/chloroprene rubber) under different stresses and temperatures by short-term creep tests (25 minutes). The creep strains data obtained were fitted to a creep model, allowing to obtain the elastic and viscous parameters of each material in the linear viscoelastic regime. It was observed that these parameters decrease with temperature for all the cases. Also, the viscoelastic constants obtained were useful to compare the creep resistance of the elastomers studied.
2. Creep phenomenon
The creep phenomenon describes the behavior of a material when it is subjected under a constant stress during long times. When a mechanical element suffers a constants stress (tension or compressive), it tends to “flow” and deforms continuously. Creep tests are usually long-term experiments. A creep test consists of applying a fixed load to a specimen and determining its deformation as a function of time. This deformation varies depending on the type of material and temperature being studied. Creep experiments can be performed in a simple way since the applied constant stress over time can be achieved by applying a dead weight to the specimen. The grip points of the specimen must be uniform in order to ensure a good distribution of the stress during the test [5]. In a complete creep test (which is carried out until the fracture of the material), the behavior of the transient strain can be described by three stages, as illustrated in Fig. 1. In the first stage, which is also called primary creep, strain occurs at a decreasing rate; in the second or secondary creep stage it increases at an almost constant rate; and in the third stage or tertiary creep, strain occurs at an increasing rate and ends in the fracture of the material [4].
The creep behavior of a material can be represented by the well-known creep compliance, D(t), which is expressed with (1).
where ε(t) is the time-dependent (creep) strain and σ 0 is the applied constant stress. In the linear viscoelastic regime, the In the Burgers model the strain ε t , is the sum of the strain (ε 1 , ε 2 and ε 3) in the three elements shown in Fig. 2a); ε 1 and ε 2 being the strains produced in the spring, R 1 and dashpot, η 1 from the Maxwell model, respectively, meanwhile ε 3 being the strain generated in the parallel connection of spring, R 2 and dashpot, η 2. The viscoelastic parameters from the Burgers model can be obtained from Fig. 2b) through creep compliance is independent on stress level, i.e., it is the same for different stresses [4]. Also, the creep compliance is related to the creep resistance of a material (low creep compliance means a high creep resistance). Thus, the resistance of a material to “flow” can be assessed in terms of creep tests determining the creep compliance.
Commonly, it is impractical to conduct long-term creep tests to know the creep behavior of a material [11-13]. Instead, short-term tests are sufficient to fit the data to creep models, and thus, predict creep for longer times. The creep phenomenon can be modeled by using standard viscoelastic models, such as the Maxwell and Kelvin-Voight standard linear solid (SLS) models. However, especially for plastics and mostly for elastomers, the 4-elements or Burgers model, which consists on a Maxwell and a Kelvin-Voight model connected in series, has been widely used since it can be accurately fitted to the behavior of these materials. The procedure of obtaining the creep model of elastomers has been published elsewhere [14,15]. Basically, it consists of obtaining the elastic and viscous parameters from the experimental data of the primary and secondary creep stage. The Burgers creep strain model may be expressed by (2) [4].
where σ 0 is the applied constant stress, R 1 and R 2 are the elastic constants and η 1 and η 2 the viscous constants.
3. Experimental
3.1. Experimental set-up
In this work, Digital Image Correlation (DIC) was implemented for strain measurement. DIC is an optical hole-field measurement technique based on the comparison of digital images of an object at different states of deformation in transient or dynamic analysis [16]. It recognizes an intensity pattern of a small area in both the undeformed and deformed images. Any point in the undeformed image is defined by the light intensity pattern from the surrounding area (usually sprayed speckle pattern paint). According to the light intensity of the point, the identical point is identified in the deformed image through tracking algorithms. Then, numerical methods are employed to compute the deformation of the set of points, generating displacement or train maps of the object surface studied. In this paper, the DIC equipment Dantec Dynamics System Q-450 was employed. This system uses a CCD camera Phantom SpeedSense 9070 (Zeiss Makro-Planar 50 mm f/2 ZF.2 lens) with image resolution of 1280 × 800 pixels. The hardware is connected to the software Istra 4D for camera configuration, image processing strain computing and graphics deployment.
On the other hand, the experimental set up shown in Fig. 3 was implemented for conducting the creep experiments. It consists of a temperature chamber with the capability of controlling temperatures up to 120°C. It integrates an electromechanical lever system for load application. The material specimen is fastened in its top and bottom sides by gripping clamps as shown in Fig. 3. In the bottom side of the specimen the dead load is applied slowly by hanging a weight stack (with a predefined weight) on the clamp through the lever system (linear actuator). When the lever displaces down, the dead load is progressively transferred to the specimen. When the weight stack hangs to the clamp, the dead load is fully transferred to the specimen producing a constant stress. The load application is synchronized with the image acquisition.
Prior to the real tests, some pre-tests (using higher loads) were conducted in order to verify if no displacements the specimen and the grips occur. It was found that no occurred even at 1 MPa. Besides, if some of these displacements occur, they would be evident when constructing the creep strain curves, e.g., a strange abrupt jump in the strain values, which did not happen.
3.2. Materials and test conditions
Five common, commercial and cross-linked engineering elastomers were considered in this study, namely Ethylene-Propylene-Diene Monomer (EPDM), neoprene/chloroprene rubber (CR), nitrile butadiene rubber (NBR), silicon rubber (VMQ) and Fluoroelastomer (Viton® or FKM). The tested samples were cut in a rectangle shape (60 × 5 mm) from commercial 2 mm thickness black sheets.
The specimens were finely specked with a white paint for allowing the contrasting pattern required for DIC. The creep tests were conducted at three levels of stress (200, 400 and 600 kPa) and three temperatures (25, 50 and 80°C). For the case of FKM, two additional temperatures were considered (100 and 120°C). The tests were run in triplicate using new specimens, without load history. Each test was run for 25 minutes, for all elastomers and conditions. The time selected was enough to generate the first and second creep stages consistently in all the cases. The image acquisition was set at 1 fps for 25 minutes.
4. Results and discussion
Linear viscoelasticity test
From the repeatability test, the average of creep strain was computed for all the test conditions. Then, in order to determine the temperature and stress regimes for which the tested materials are linear viscoelastic, the creep compliances (1) for each stress and temperature were obtained. It is important to point out that before fitting a creep model to the experimental data, it is necessary to determine the linear viscoelastic regimes. Some examples of the obtained creep compliances are shown in Fig. 4 (for CR) and 5 (for FKM). According to the definition of the linear viscoelastic behavior, the creep compliance for different stresses at a certain temperature should be equal. Thus, for the cases where the creep compliance curves are similar, it could be said the material is linear viscoelastic. For example, in Fig. 4, it can be observed that at room temperature (25°C) the creep compliance curves of the three stresses almost overlap, indicating that at that temperature and until 600 kPa CR is linear viscoelastic. However, at 50°C and 80°C in Figs. 4b) and 4c) the creep compliances for 200 kPa and 400 kPa remain similar but for 600 kPa are completely different. Therefore, it can be inferred that at 50°C and 80°C CR is linear viscoelastic only at a maximum stress of 400 kPa.
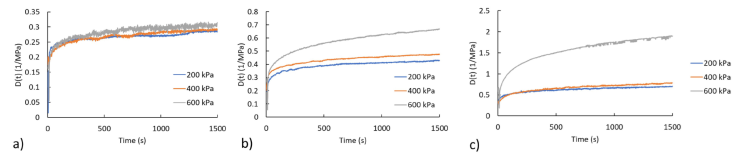
Figure 4 Creep compliances of the three stresses obtained for CR at different temperatures: a) 25°C, b) 50°C and c) 80°C.
On the other hand, from Fig. 5 it can be observed that the creep compliance curves of the three stresses are almost similar, even at 100°. In fact, FKM was found to be linear viscoelastic at 120°C and 600 kPa. This analysis was applied to the other three materials. In Table I, the temperature and stress conditions of linear viscoelastic behavior of the five materials are summarized. VMQ was linear viscoelastic only at room temperature with a maximum stress of 400 kPa. It can be also observed that the material with a wide range of linear viscoelastic regime was FKM.
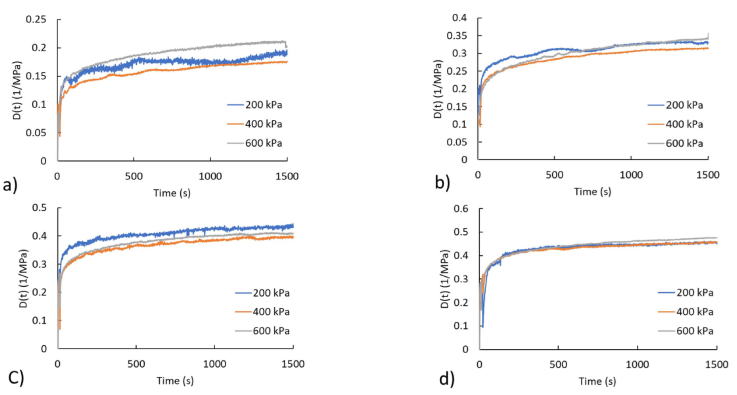
Figure 5 Creep compliances of the three stresses obtained for FKM at different temperatures: a) 25°C, b) 50°C, c) 80°C and d) 100°C.
Table I Temperature and maximum stress conditions for linear viscoelastic behavior of the tested materials.
| Material | Temperature (°C) | Maximun Stress (kPa) |
|---|---|---|
| 25 | ||
| EPDM | 50 | 400 |
| 80 | ||
| 25 | 600 | |
| CR | 50 | 400 |
| 80 | ||
| NBR | 25 | 400 |
| 50 | ||
| VMQ | 25 | 400 |
| 25 | ||
| 50 | ||
| FKM | 80 | 600 |
| 100 | ||
| 120 |
Once the conditions of linear viscoelastic behavior were identified, now it is possible to determine the elastic and viscous parameters (in the linear viscoelastic regime) of each material by fitting the creep data to the viscoelastic Burgers model, which is known to describe very well the viscoelastic behavior of most of the elastomers [14,15]. Thus, the average creep curves of each stress and temperature condition reported in Table I were fitted to the Burgers creep model Eq. (2).
The plots of the experimental creep strains as well as their respective fitted models for the stresses and temperatures in the linear viscoelastic regime are shown in Figs. 6-10. It can be observed that for the five elastomers the creep increases with temperature. It can be seen that EPDM and Neoprene (CR) have a similar creep behavior in Figs. 6 and 7. However, at the highest stress (600 kPa) and at room temperature CR still behaves linearly viscoelastic.
On the other hand, for NBR Fig. 8, a moderate creep strain can be observed even at the highest temperatures. However, NBR was found to be linear viscoelastic only until 400 kPa and 50°C.
Silicon rubber (VMQ) exhibited a particular behavior Fig. 9. A large instantaneous (elastic) strain and a very small viscous deformation, i.e., curves with a small slope, can be observed. An obvious implication of this behavior is that the strain does not increase considerably in the long-term.
In the case of Viton (FKM), additional tests were conducted since it was observed that it exhibited a high creep resistance in comparison with the other elastomers. Thus, this elastomer was also tested at 100 and 120°C for the three stresses. According to the creep compliance tests mentioned before and summarized in Table I, FKM was found to behave linearly viscoelastic even at the highest stress (600 kPa) and temperature (120°C). Moreover, FKM does not exhibit a high instantaneous strain as the VMQ, as can be observed in Fig. 10. Instead, it is characterized by a steady and moderate increase of strain with time, which can be understood as an equilibrium between elastic and viscous behavior. It is noteworthy that this elastomer can endure higher temperatures without an excessive creep deformation. However, because of the limitation of the temperature chamber, temperatures above 120°C cannot be reached. It is also important to mention that for the other elastomers, extra tests were conducted at temperatures > 80 C, however it was observed that in almost all the cases the samples reached the third stage of creep and fractured. Hence, it can be concluded that, in the case of tensile creep, the elastomer with the best resistance to creep is the Fluoroelastomer (Viton® or FKM) rubber.
In order to quantify the degree of correlation between the prediction model and the experimental data, the coefficient of determination for all the cases was calculated and is reported in Table II. The main sources of error could be: 1) rigid body motion and 2) calibration error (DIC system).
Table II Errors of the fitted models.
| Material |
|
|
R 2 |
|---|---|---|---|
| 200 | 25 | 0.89 | |
| 50 | 0.93 | ||
| EPDM | 80 | 0.94 | |
| 400 | 25 | 0.95 | |
| 50 | 0.92 | ||
| 80 | 0.84 | ||
| 200 | 25 | 0.86 | |
| 50 | 0.95 | ||
| 80 | 0.97 | ||
| CR | 400 | 25 | 0.91 |
| 50 | 0.95 | ||
| 80 | 0.98 | ||
| 600 | 25 | 0.88 | |
| 200 | 25 | 0.92 | |
| NBR | 50 | 0.85 | |
| 400 | 25 | 0.9 | |
| 50 | 0.93 | ||
| VMQ | 200 | 25 | 0.82 |
| 400 | 25 | 0.84 | |
| 200 | 25 | 0.87 | |
| 50 | 0.92 | ||
| 80 | 0.94 | ||
| 100 | 0.89 | ||
| 120 | 0.9 | ||
| FKM | 400 | 25 | 0.91 |
| 50 | 0.94 | ||
| 80 | 0.94 | ||
| 100 | 0.96 | ||
| 120 | 0.92 | ||
| 600 | 25 | 0.91 | |
| 50 | 0.95 | ||
| 80 | 0.94 | ||
| 100 | 0.96 | ||
| 120 | 0.96 |
According to the theory of the linear viscoelasticity, when a material works in its linear viscoelastic regime, it should have the same elastic and viscous constants at any level of stress. Thus, once the creep functions were obtained, the elastic and viscous parameters (R 1, R 2, η 1, η 2, from (2)) of the stresses at each temperature can be averaged, in order to fully characterize the viscoelastic behavior of the tested elastomers. The average of each parameter of the five elastomers are summarized in Table III. These constants give a much more quantitative illustration of the resistance the elastomers to the creep phenomenon. R 1, and R 2 represent the elastic responses and η 1 and η 2 the viscous behavior. Specially, the values of R 1 and η 1 dictate the creep strength of the materials. In Table III it can be seen that the lower values of R 1 correspond to VMQ, which explains the large instantaneous strains (i.e., lower elastic resistance). Also, the same material presented the higher values of η 1, which explains the low viscous strain. On the other hand, FKM exhibited the higher elastic constant R 1 and also high viscous constant η 1. Finally, EPDM and CR presented the lower viscous constants. For all the cases, these constants decrease with temperature.The percentages of degradation of each parameter with respect to the room temperature are reported in Table IV.
Table III Elastic and viscous parameter of the tested materials.
| Material | Temperature (°C) | R 1 (MPa) | R 2 (MPa) | η 1 (MPa.s) | η 2 (MPa.s) | Maximum Stress (kPa) |
|---|---|---|---|---|---|---|
| 25 | 10.00 | 5.71 | 28646.66 | 203.34 | ||
| EPDM | 50 | 6.46 | 5.00 | 22916.80 | 146.38 | 400 |
| 80 | 4.85 | 2.35 | 11456.22 | 97.32 | ||
| 25 | 6.24 | 11.15 | 32738.47 | 284.28 | 600 | |
| CR | 50 | 4.60 | 6.41 | 17627.54 | 287.47 | 400 |
| 80 | 2.78 | 4.44 | 9545.78 | 353.66 | ||
| 25 | 10.00 | 11.27 | 57295.06 | 235.61 | ||
| NBR | 50 | 8.00 | 8.89 | 38196.22 | 236.10 | 400 |
| 80 | - | - | - | - | ||
| 25 | 3.27 | 10.00 | 152788.17 | 235.01 | 400 | |
| VQM | 50 | - | - | - | - | |
| 80 | - | - | - | - | ||
| 25 | 14.35 | 11.02 | 52085.76 | 434.86 | ||
| 50 | 6.82 | 7.71 | 23870.58 | 242.81 | ||
| FKM | 80 | 4.39 | 7.71 | 22915.54 | 348.03 | 600 |
| 100 | 4.15 | 6.35 | 22915.54 | 352.17 | ||
| 120 | 3.27 | 6.24 | 22915.54 | 233.23 |
Table IV Percentage of change in the viscoelastic parameters of the elastomer due to temperature.
| Material | Temperature (°C) | R 1 | R 2 | η 1 | η 2 |
|---|---|---|---|---|---|
| EPDM | 50 | 35.42 | 12.50 | 20.00 | 28.01 |
| 80 | 51.47 | 58.82 | 60.01 | 52.14 | |
| CR | 50 | 26.26 | 42.51 | 46.16 | 1.12 |
| 80 | 55.47 | 60.14 | 70.84 | 24.41 | |
| NBR | 50 | 25.00 | 26.72 | 50.00 | 0.21 |
| 50 | 52.48 | 29.97 | 54.17 | 44.16 | |
| FKM | 80 | 69.40 | 29.97 | 56.00 | 19.97 |
| 100 | 71.10 | 42.36 | 56.00 | 19.01 | |
| 120 | 77.23 | 43.35 | 56.00 | 46.37 |
It can be observed from Table IV that temperature can reduce the viscoelastic parameters of the elastomers. It is interesting to note that at 50°C, FKM reduces more than 50% of its elastic parameter R 1, whereas for CR and EPDM it is only reduced 26% and 35%, respectively. However, it should also be observed that the other parameters of FKM do not seem to be reduced considerably, comparing with EPDM, CR and NBR. VMQ does not appear in Table IV since it was found to be linear viscoelastic only at room temperature. Once the viscoelastic parameters were obtained, the creep compliance curves of each material can be constructed. In Figs. 11-13, the creep compliance curves of the five elastomers, in their previously established linear viscoelastic regime and for 1500 s, are presented. From Fig. 11 it can be observed that EPDM and CR have similar creep compliance curves, reaching a maximum creep compliance of ≈ 0.8 MPa, which means that they have similar behavior under creep phenomenon. Also, they were linear viscoelastic at 80°C and 400 kPa. From Fig. 12 the creep compliance of NBR and VMQ can be seen. For the case of NBR, the maximum creep compliance (at 50°C) was ≈ 0.3 MPa, which is less than that obtained for EPDM and CR at the same temperature. On the other hand, for VMQ, a single curve is available, which correspond to a maximum stress of 400 kPa and 25°C.
Finally, in Fig. 13, the creep compliance curves of FKM can be observed. Note that the highest creep compliance reached (at 120°C) is even smaller than that obtained for EPDM and CR at 80°C. Through a visual comparison of the curves in Figs. 11-13 it can be said that FKM is the most resistant to tensile creep, since exhibited the lowest creep compliance values. This can be also observed quantitatively from Table III.
5. Conclusions
In this work a simple and effective experimental set-up of creep tests, integrated with a digital image correlation measurement system was successfully applied for the construction of creep curves of elastomers. In this paper, a comparison of the creep behavior of five common engineering elastomers (Ethylene-Propylene-Diene Monomer (EPDM), neoprene/chloroprene rubber (CR), nitrile butadiene rubber (NBR), silicon rubber (VMQ) and Fluoroelastomer (VitonⓇ or FKM)) is presented. 25 minutes creep test were conducted at different stresses and temperatures and the linear viscoelastic regimes were evaluated and then, the creep curves were fitted to the Burgers creep model. For all the materials and conditions, the first and second stages of creep were deployed, which was suitable for fitting the data to a model, enabling to predict strains for further times. The effect of temperature on the viscoelastic parameter of the five elastomers was evaluated. It was found that exists a generalized decrease on the values of the elastic and viscous parameters with temperature. From the creep curves obtained, it was observed that VMQ exhibited the highest elastic behavior (small elastic parameter) but small viscous deformation (high viscous parameters) and a narrow linear viscoelastic regime (25°C and 40 kPa). NBR also showed a narrow linear viscoelastic regime but resist until 50°C and 400 kPa. EPDM, Neoprene (CR) were found to be still linear viscoelastic at 80°C but at a maximum stress of 400 kPa. On the other hand, Fluoroelastomer (FKM) rubber showed moderate creep strain curves, even at 100 and 120°C. Moreover, it was found that FKM has the widest linear viscoelastic regime, behaving still linear viscoelastic at 600 kPa and 120°C. In summary, the results obtained in this work showed that FKM has the highest tensile creep resistance at high temperatures. Finally, though it was not the main objective of this work, from extra tests it was demonstrated that the experimental system is versatile for recovery measurement.











 nueva página del texto (beta)
nueva página del texto (beta)













