On the radiative and multiple reflection corrections of the van der Waals force between two particles/atoms: dipolar contribution

Zurita-Sánchez, Jorge R.; Zurita-Sánchez, Jorge R.

doi:10.31349/revmexfis.69.040403

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.69 no.4 México jul./ago. 2023 Epub 19-Nov-2024

https://doi.org/10.31349/revmexfis.69.040403

Atomic and molecular physics

On the radiative and multiple reflection corrections of the van der Waals force between two particles/atoms: dipolar contribution

Jorge R. Zurita-Sánchez^a

^{^a} Instituto Nacional de Astrofísica, Óptica y Electrónica; Luis Enrique Erro 1, Tonantzintla, Pue. 72840, México.

ABSTRACT

We present a theoretical formalism based on fluctuational electrodynamics and the Maxwell-stress tensor for describing the impact of radiative and multiple reflections corrections on the van der Waals force between two nanoscale spherical particles and a pair of atoms in the dipolar approximation. Particularly, we examine the van der Waals forces for two metallic particles whose dielectric constant is represented by the Drude model, for two dielectric particles in which their material response has phononic resonances, and for two atoms with dynamic polarizabilities containing a single resonant frequency. For the metallic particles, in relation to the case in which the aforementioned effects are omitted, the van der Waals force is unchanged by the radiative corrections of the polarizabilities, whereas the mechanism of multiple reflections perturbs force about a few percentage points when the spheres nearly touch each other. In contrast to the metallic case, the radiative corrections of the polarizabilities of the dielectric particles modify peculiarly the van der Waals force in comparison to the case where such corrections are neglected; there is a critical interparticle separation that divides two regimes: when the interparticle separation is smaller (larger) than this critical distance the force with radiative corrections is smaller (greater) than that without these corrections. Moreover, the van der Waals force is practically unchanged when effect of multiple reflections is taken into account. For the atomic case, the deviation of the van der Waals force due to multiple reflections is about a few percentage points when the interatomic separation corresponds to twice the van der Waals radius, and this deviation can reach about seventeen percent at a separation of 2.5 times the atomic radius. This work might have implications concerning the fine-tuning between theoretical and experimental outcomes of the van der Waals forces.

Keywords: Van der Waals force; Casimir force; electromagnetic fluctuations

1 Introduction

The presence of electromagnetic fluctuations in matter and space is ineludible; they still exist at absolute zero temperature, which are the so-called vacuum fluctuations. As a consequence of these fluctuations, forces between neutral atoms or macroscopic objects arise ^[1, ^2], and they are denominated as van der Waals or Casimir forces. We mention that van der Waals forces are usually associated with interaction of particles or atoms, whereas Casimir forces involve macroscopic objects. The van der Waals forces take part in stability of some inorganic materials ^[3, ^4] as well in biological elements ^[5, ^6]. Also Casimir forces can impact the performance of the motion on micro- and nano-mechanical devices ^[7]. Recent research of Casimir forces is related to new materials such as metamaterials ^[8], graphene ^[9], topological insulators ^[10], Weyl-semimetals ^[11], complex geometries ^[12, ^13], as well as conditions out of thermal equilibrium ^[14, ^15]. Since there exists a very vast literature about this topic, we refer to the reader to the following texts ^[16, ^17, ^18, ^19].

The current technological capabilities for manipulating and fabricating nano- and atomic-structures have allowed the continuous improving of the accuracy for measuring van der Waals or Casimir forces. However, there are still discrepancies between the experimental outcomes and theoretical predictions. There is a long list of causes that gives rise to such discrepancies. For example, since the theoretical formalism of these forces demands the a priori knowledge of the dielectric function of the particles in the whole electromagnetic spectrum, sometimes this information is not available, in other cases, the models of the dielectric function can yield inaccurate estimations of the dielectric response of the material in some spectral ranges ^[20, ^21]. Moreover, the superficial roughness of realistic objects can yield significant deviation of experimental outcomes of the Casimir force from the calculation of the force arising from a smooth surface ^[22, ^23]. Moreover, the van der Waals force between two noble gas atoms was measured with a functionalized tip of an atomic force microscope, obtaining, in comparison with the case of isolated atoms, a stronger interaction due to adsorption effects in the setup; also the van der Waals potential energy deviates from the theoretical power law when heavy atoms interact ^[24].

Herein we explore another mechanisms that could influence the theoretical outcome. Our aim is to analyze until what extent the van der Waals force between two spherical particles is perturbed when multiple scattering and radiative corrections of the polarizabilities are considered; the influence on the van der Waals force due to the multiple reflections is also examined for two atoms.

Our paper is organized as follows. Section 2 presents the theoretical formalism for obtaining the van der Waals force between two spherical particles when the effect of multiple reflections and radiative corrections of the polarizabilities are taken into account. This section is complemented by two Appendices. In Sec. 3, the results for three different scenarios are shown; van der Waals forces for metallic and dielectric particles, and for a pair of atoms. Section 4 contains the conclusions.

2 Theory

We consider a spherical particle that is located at rs=dnz (center), and it has radius a _s and frequency-dependent dielectric function ϵs(ω); ω is the angular frequency and nz is the Cartesian unit vector in the direction of the z-axis. In the vicinity of this particle, there exists another spherical particle, whose center position, radius, and dielectric function are rp=0, ap, and ϵp(ω), respectively. The nonabsorbing environment in which the particles are embedded has dielectric constant ϵ1. Furthermore, we assume that the environment and particles are non-magnetic, and they are held at temperature T, that is, the whole system is at thermal equilibrium. This setup is depicted in Fig. 1a).

To calculate the van der Waals force due to vacuum and thermal fluctuations that is exerted on any of these particles, we require the electric response of an arbitrary electric dipole located at the background medium in presence of the two particles; as will be seen, the electromagnetic field correlations of vacuum and thermal fluctuations are needed for obtaining the force and they depend on this response. Then, the electric response is expressed as

E(r)=k12ε0ϵ1G↔(r,r0,ω)⋅p (1)

where E(r) is the electric field generated by the dipole, ε0 is the vacuum permittivity, k1=ωϵ1/c (c is the speed of light in vacuum), G↔ is the Green tensor, and p and r0 are the moment and position of the dipole, respectively. It turns out that the Green tensor for our setup is explicitly

Gil(r,r0,ω)=G0il(r,r0,ω)+k12ε0ϵ1αp(ω)βj(k1d)×G0ij(r,0,ω)G0jl(0,r0,ω)+k12ε0ϵ1×αs(ω)βj(k1d)G0ij(r,dnz,ω)G0jl(dnz,r0,ω)+14πk15(ε0ϵ1)2αp(ω)αs(ω)ξj(k1d)βj(k1d)G0ij(r,0,ω)G0jl(dnz,r0,ω)+G0ij(r,dnz,ω)G0jl(0,r0,ω) (2)

where i, j, l = x, y, z, G0il is the Green tensor of the bulk medium (background without particles) which is explicitly

G↔0(r,r',ω)=I↔+∇∇k12exp(ik1|r-r'|)4π|r-r'|, (3)

(I↔ is the unit dyadic). Here, αν(ω) (v = p, s) is the polarizability with radiative correction, given by

αν(ω)=α~ν(ω)/Γν, (4)

where α~ν(ω) is the static polarizability and Γν is the radiative correction factor, which are given by

α~ν(ω)=4πaν3ϵ0ϵ1(ϵν-ϵ1)ϵν+2ϵ1, (5)

Γν=1-ik136πϵ0ϵ1α~ν(ω). (6)

The factors ξi(k1d) are defined as

ξx(k1d)=ξy(k1d)=exp⁡ik1d(k1d)3(k1d)2+ik1d-1) (7)

ξz(k1d)=2exp(ik1d)(k1d)3(-ik1d+1), (8)

and βi are the factors arising from multiple scattering which are given by

βi(k1d)=1-k16(4πε0ϵ1)2αp(ω)αs(ω)ξi2(k1d) (9)

The five additive terms of the right-hand side of Eq. (2) correspond respectively to the interacting paths I, II, III, IV, and V of Fig. 1b). The derivation of Green tensor Eq. (2) is found in Appendix A.

Figure 1 a) Setup. b) The five interacting path of the Green tensor.

2.1 Force

The background medium is vacuum hereafter, thus ϵ1=1. The force (along the axis joining the centers of the particles) that is exerted on the particle located at the origin is calculated from

Fz=∮∂V‍〈Txz〉 dax+〈Tyz〉 day+〈Tzz〉 daz (10)

Here, 〈…〉 denotes ensemble average, T_ij (i, j, = x, y, z) are the Cartesian components of the Maxwell stress tensor which are given by

Tij=ε0EiEj-δ~ijε0E2/2+μ0HiHj-δ~ijμ0H2/2 (11)

where δ~ij is the Kronecker-δ tensor, μ0 is the vacuum permeability, E_i and H_i are the Cartesian components of the fluctuating electric and magnetic fields, respectively. The integration is carried over the spherical surface rc=bnr (ap<b<d-as) which encloses the aforementioned particle; da_i (i = x, y, z) are the Cartesian components of a differential segment of area of this surface, that is, da=b2sinθdθdϕnr where nr is the unit vector along the radial direction, and θ and ϕ are the polar and azimuthal angles, respectively.

By using the properties of the stochastic thermal fields corresponding to our environment, the force Eq. (10) turns out to be

Fz=ℏ4π3ε02d7∫0∞Im{αp(ω)αs(ω)e2ikdg1(kd)γ1(k,d)+g2(kd)γ2(k,d)}1/2+Θ(ω,T)dω. (12)

Here, Im{…} denotes imaginary part, k=ω/c, Θ(ω,T)={expℏω/(kBT)-1}-1 is the mean photon number,

g1(kd)=-i(kd)5+3(kd)4+6i(kd)3-8(kd)2-6ikd+3 (13)

g2(kd)=2(i(kd)3-4(kd)2-6ikd+3) (14)

γ1(k,d)=1-1(4πε0)2d6αp(ω)αs(ω)e2ikd(kd)4+2i(kd)3-3(kd)2-2ikd+1, (15)

γ2(k,d)=1-4(4πε0)2d6αp(ω)αs(ω)e2ikd-(kd)2-2ikd+1 (16)

ℏ and k_B are the reduced Planck and Boltzmann constants, respectively. Equation (12) is derived in Appendix B. We mention that if the multiple scattering effect is neglected, that is, second terms of the right-hand side of (15) and (16) are disregarded, then the conventional formula of the van der Waals force is recovered.

3 Results

To determine how strong is the impact of the polarizabilities with radiative corrections and the effect of multiple reflections on the van der Waals force, we examine three particular cases. The first one considers that the particles are metallic, whereas the second case involves the interaction between dielectric particles. The last case deals with the force between a pair of atoms. The temperature for all cases is set to T = 0 K, thus only the contribution arising from vacuum fluctuations is considered.

3.1 Metallic Particles

We consider that the size and dielectric functions of the metallic particles are the same, namely, a = a_p = a_s and ϵ=ϵp=ϵs. Furthermore, the dielectric function of the metallic particles is described by the Drude model as

ϵ(ω)=ϵ∞-ωp2ω2+iγω, (17)

where ωp is the plasma frequency, γ is the collision rate, and ϵ∞ is the dielectric function in the limit ω→∞. In particular, we assume that these parameters have the following values: ωp/c=5×10-2 nm-1 γ/ωp=2.4×10-3, and ϵ∞=1; these values are of the order of those that correspond to the dielectric function of noble metals due to free-charge carriers ^[25].

Figure 2 depicts the force F_z for several radii of particles as a function of the separation d; three curves are shown for each particle size: (1) the curve that considers only the static polarizabilities of particles without the effect of multiple reflections, denominated simply as “static case"; (2) the curve that comes from polarizabilities with radiative corrections and excludes multiple reflections, denominated as “radiative case"; (3) the curve that takes into account both polarizabilities with radiative corrections and the effect of multiple reflections, named “multireflection case". As seen in the curves of Fig. 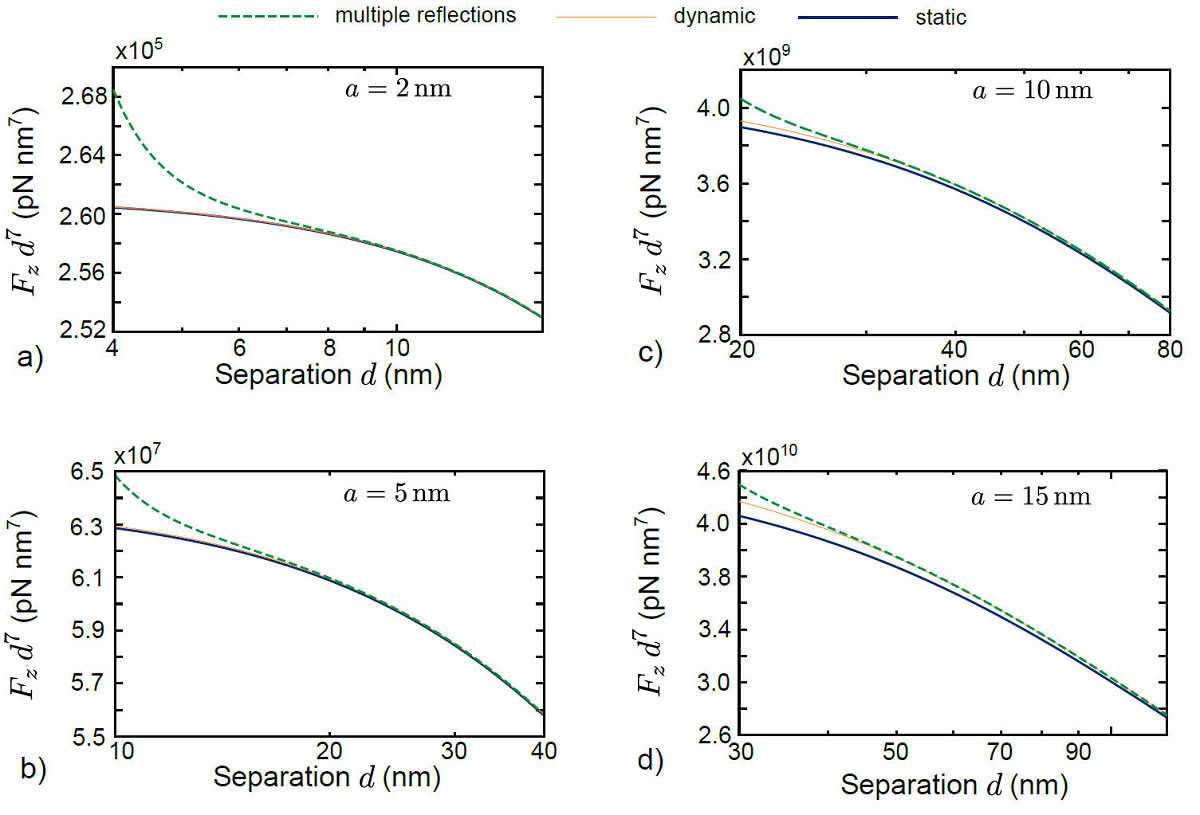2, the information of the force F_z versus separation d is indirectly provided since the vertical axis of these curves is Fzd7, thus this information is extracted by dividing the strength of the curves by the factor d⁷. The reason for this presentation is that the deviation of the force from the London dispersion force law (∝d-7) can be easily visualized; this applies for the rest of the curves that are shown ahead.

Figure 2 Van der Waals forces for metallic particles; static, radiative, and multireflection cases. F_z d⁷ versus d. a) a = 2nm. b) a = 5nm. c) a = 10nm. d) a = 15nm. For these plots, 2a<d<8a.

By disregarding the effect of the multiple reflections, when a = 2nm (Fig. 2a)), we notice that there is practically no difference between the curves corresponding to the static and radiative cases. However, by comparing Figs. 2a)-d), as the radius of the particles increases, the difference between these curves grows; the strength force for the radiative case is larger than that for the static case. By considering the effect of multiple reflections, we notice that, in comparison with the radiative case, the force is perturbed; as seen in Figs. 2a)-d), the multireflection effect becomes appreciable in the range 2a<d≲4a and the deviation between these curves is approximately 3% when the spheres almost touch each other (d→2a). We mention that as d approaches to the contact point (d=2a) of the spheres, multipolar contributions of high-order must be taken into account.

3.2 Dielectric particles

We now consider two identical dielectric particles; the nomenclature is the same as previous case (a=ap=as and ϵ=ϵp=ϵs). For this case, we assume that the dielectric function of the particles has phononic resonances. This material can be described by a single oscillator model, that is,

ϵ(ω)=ϵ∞1+ωA2ωT2-ω2-iΓω, (18)

where ωT is the resonant frequency of the transverse-optical phonon, ωA2=ωL2-ωT2 (ωL2 being the frequency of the longitudinal-optical phonon), Γ is the damping factor. The parameters are set to those that correspond approximately to SiC ^[26]: ωT/c=5×10-4 nm-1, Γ/ωT=0.006, ωA/c=3.5×10-4 nm-1, and ϵ∞=6.7.

We keep the same shorthand as in previous subsection when we refer to “static", “radiative", and “multireflection" cases. Figure 3 illustrates the force F_z versus the separation d for the static, radiative, and multireflection cases and different particle sizes.

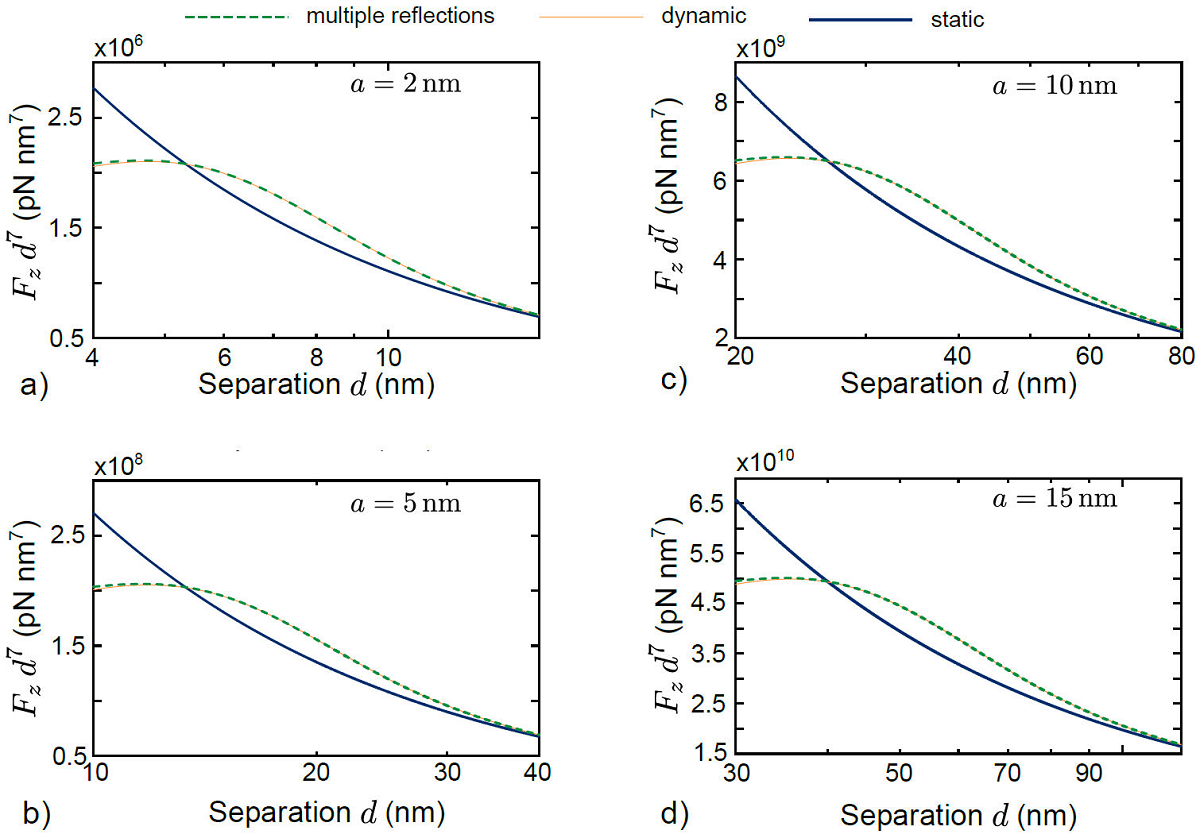
Figure 3 Van der Waals forces for dielectric particles; static, radiative, and multireflection cases. F_z d⁷ versus d. a) a = 2nm.. b) a = 5nm. c) a = 10nm. d) a = 10nm. For these plots, 2a<d<8a.

We notice that the curves for the static and radiative cases intersect; the crossing point is denoted d_c . When d < d_c , the strength of the force is larger for the static case than that for the radiative case. For a particular particle size, the largest difference occurs when d = 2a and it is about 34.6%. On the contrary, when d < d_c , the magnitude of the force for the radiative case exceeds the one for the static case; maximum difference is about 14.7% and it happens when d = 3.61a. Moreover, the crossing point of the aforementioned curves is located at dc≈8a/3. In comparison to the radiative curve, the impact of the multiple reflections is practically null; there is a slight perturbation when particles nearly touch. The comparison of the figures for different sizes of particles, together with the aforementioned features, suggests a proportionality connection among them. By defining Φ(d,a)≡Fz(d,a)d7 and two different sets of two-equal-size particles (radii a₁ and a₂), we found the relation:

Φ(fa1,a1)/Φ(fa2,a2)=(a1/a2)5 (19)

that applies, at least, in the range 2 < f < 8 where f is a dimensionless factor.

3.3 Atoms

We extrapolate the Eq. (12) for calculating the van der Waals force between two identical atoms due to vacuum fluctuations. Consequently, we replaced the polarizabilities αs and αp by the atomic polarizability α(ω) which is expressed as ^[27]

α(ω)=|μ|2ℏ1ω0-ω-iΥ/2+1ω0+ω+iΥ/2 (20)

where μ is the transition dipole moment, ω0 is the resonant frequency with linewidth Υ; this description assumes only a single resonance.

To find the impact of multiple reflections, we consider the atomic pair Ca-Ca. The atomic radius of Ca is Ra=180pm, whereas, for this pair of atoms, the van der Waal radius is Rw=262pm ^[28]. The experimental dipole-dipole van der Waals coefficient is C6=2188Eha06 (Eh is the Hartree energy and a0 is the Bohr radius) ^[29]; the interacting potential is U=-C6/(d6). For the atomic force, we consider two cases: the first one in which the multireflection terms are neglected, denominated as the “conventional case”; the second takes into account the effect of multiple reflections, known as the “multireflection case”. Figure 4 depicts the van der Waals force against the interatomic separation d for the conventional and multireflection cases. We have set ω0/c=0.01nm-1, Υ/ω0=0.001, and μ=1.2922 eÅ (e is the electron’s charge); these parameters yield a force curve for the conventional case that coincides exactly with the curve that arises from the aforementioned interaction involving coefficient C₆, as seen in Fig. 4. In comparison with the conventional case, the effect of multiple reflection influences noticeably the van der Waals force in the range d<2Rw. When the separation is d=2Rw, the deviation from curve corresponding to the conventional case is about 5.88 %, whereas this deviation grows to 17% for an interatomic separation d=2.5Ra. However, when the atoms get closer, contributions of high-order become important ^[29]; also if the atomic clouds overlap, the electronic interaction becomes complex ^[18, ^19].

Figure 4 Van der Waals force for a Ca-Ca pair. F_z d⁷ versus separation d for conventional and multireflection cases. The distances 2.5 R_a and 2R_w are indicated with vertical dashed lines.

3.4 Additional remarks

The frequency-integrals have been carried out numerically by the methods of ^[30, ^31]. For illustrative purposes, we have considered simple models for describing the dielectric function of a metal or dielectric. However, the modelling of the dielectric function for a realistic material is more complex. For example, the electric response of a noble metal, in addition to the the contribution of free-electrons, comes from bound electrons (interband transitions) which are important in the optical spectrum; this contribution can be described by using the expression Eq. (18). With this limitation, our results are intended for presenting an estimation of the impact of the effect of multiple reflection and the radiative corrections of the polarizabilities of particles.

4 Conclusions

We have derived the analytical expression for calculating the van der Waals force in a setup composed of two spherical particles that takes into account the multiple reflections and the radiative correction of the polarizabilities (dipole-dipole interaction). To determine the influence of these effects, we have obtained the van der Waals for three particular cases: metallic particles, dielectric particles, and a pair of atoms.

The dielectric response of the metal was described by the Drude metal. In comparison with the case where the aforementioned mechanisms are neglected, the van der Waals force is practically unperturbed by radiative correction of the polarizabilities, whereas the effect of multiple reflections causes a deviation of the force at most of a few percentage points when the spheres are close to each other (2a<d<3a).

A single oscillator model was considered for the dielectric particles. The van der Waals force suffers a noticeable and peculiar perturbation when the radiation corrections to the polarizabilities are considered. The van der Waals force with these corrections is smaller than that without them when d≲8a/3, whereas, the opposite happens when d≳8a/3. Different from the case of metallic particles, the van der Waals force practically is unchanged with the inclusion of multiple reflections.

In the atomic case, the polarizability of each of the atoms is described by a single resonance. The effect of multiple reflections changes with respect to the van der Waals force law d^-7; the force difference between these curves at equilibrium separation (d=2Rw) is also a few percentage points and it grows to about 17% when d=2.5Ra.

Our work might have repercussions related to fine adjustments between theory and experiments of the van der Waals interaction between particles.

Acknowledgements

JRZ-S thanks Prof. Carsten Henkel from Universität Potsdam for his valuable feedback about some aspects of the content of this paper.

References

[1] F. London, The general theory of molecular forces, Trans. Faraday Soc. 33 (1937) 8b. [ Links ]

[2] H. G. B. Casimir, On the attraction between two perfectly conducting plates, Proc. Kon. Ned. Akad. Wetensch. B 51 (1948) 793. [ Links ]

[3] C. Kittel, Introduction to Solid State Physics, chap. 3, pp. 49-60, 8th ed. (John Wiley & Sons, Hoboken, NJ, 2005). [ Links ]

[4] G.-X. Zhang, A. Tkatchenko, J. Paier, H. Appel, and M. Scheffler, Van der Waals interactions in ionic and semiconductor solids, Phys. Rev. Lett. 107 (2011) 245501. [ Links ]

[5] D. Leckband and S. Sivasankar, Forces controlling protein interactions: theory and experiment, Colloid Surf. B 14 (1999) 83. [ Links ]

[6] B. Kollmitzer, P. Heftberger, R. Podgornik, J. F. Nagle, and G. Pabst, Bending rigidities and interdomain forces in membranes with coexisting lipid domains, Biophys. J. 108 (2015) 2833. [ Links ]

[7] F. M. Serry, D. Walliser, and G. J. Maclay, The role of the Casimir effect in the static deflection and stiction of membrane strips in microelectromechanical systems (MEMS), J. Appl. Phys. 84 (1998) 2501. [ Links ]

[8] C. Henkel and K. Joulain, Casimir force between designed materials: What is possible and what not, Europhys. Lett. 72 (2005) 929 [ Links ]

[9] J. F. Dobson, T. Gould, and G. Vignale, How many-body effects modify the van der Waals interaction between graphene sheets, Phys. Rev. X 4 (2014) 021040. [ Links ]

[10] W. Nie, R. Zeng, Y. Lan, and S. Zhu, Casimir force between topological insulator slabs, Phys. Rev. B 88 (2013) 085421. [ Links ]

[11] J. H. Wilson, A. A. Allocca, and V. Galitski, Repulsive Casimir force between Weyl semimetals, Phys. Rev. B 91 (2015) 235115. [ Links ]

[12] M. F. Maghrebi, S. J. Rahi, T. Emig, N. Graham, R. L. Jaffe, and M. Kardar, Analytical results on Casimir forces for conductors with edges and tips, P. Natl. Acad. Sci. USA 108 (2011) 6867. [ Links ]

[13] M. Levin, A. P. McCauley, A. W. Rodriguez, M. T. Homer Reid, and S. G. Johnson, Casimir repulsion between metallic objects in vacuum, Phys. Rev. Lett. 105 (2010) 090403. [ Links ]

[14] M. Antezza, Surface-atom force out of equilibrium and its effect on ultra-cold atoms, J.Phys. A: Math. Gen. 39 (2006) 6117. [ Links ]

[15] M. Krüger, T. Emig, and M. Kardar, Nonequilibrium electromagnetic fluctuations: Heat transfer and interactions, Phys. Rev. Lett. 106 (2011) 210404. [ Links ]

[16] V. A. Parsegian, Van der Waals Forces (Cambridge University Press, New York, NY, 2006). [ Links ]

[17] D. Dalvit, P. Milonni, D. Roberts, and F. da Rosa, eds., Casimir Physics, Lecture Notes in Physics (Springer, Berlin, 2011). [ Links ]

[18] L. M. Woods, D. A. R. Dalvit, A. Tkatchenko, P. Rodriguez-Lopez, A. W. Rodriguez, and R. Podgornik, Materials perspective on Casimir and van der Waals interactions, Rev. Mod. Phys. 88 (2016) 045003. [ Links ]

[19] J. Herman, R. A. DiStasio Jr., and A. Tkatchenko, First-principles models for van der Waals interactions in molecules and materials: Concepts, theory, and applications, Chem. Rev. 117 (2017) 4714 [ Links ]

[20] P. J. van Zwol, G. Palasantzas, and J. Th. M. De Hosson, Influence of dielectric properties on van der Waals/Casimir forces in solid-liquid systems, Phys. Rev. B 79 (2009) 195428. [ Links ]

[21] M. M. Gudarzi and S. H. Aboutabelu, Self-consistent dielectric functions of materials: Toward accurate computation of Casimir-van der Waals forces, Sci. Adv. 7 (2021) eabg2272. [ Links ]

[22] P. J. van Zwol, G. Palasantzas, and J. Th. M. De Hosson, Influence of random roughness on the Casimir force at small separations, Phys. Rev. B 77 (2008) 075412. [ Links ]

[23] W. Broer, G. Palasantzas, J. Knoester, and V. B. Svetovoy, Significance of the Casimir force and surface roughness for actuation dynamics of MEMS, Phys. Rev. B 87 (2013) 125413. [ Links ]

[24] S. Kawai et al., Van der Waals interactions and the limits of isolated atom models at interfaces, Nat. Comm. 7 (2016) 11559. [ Links ]

[25] M. A. Ordal, R. J. Bell, R. W. Alexander, L. L. Long, and M. R. Querry, Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W, Appl. Opt. 24 (1985) 4493. [ Links ]

[26] W. J. Choyke and E. D. Palik, Handbook of Optical Constants of Solids, chap. Silicon Carbide (SiC), pp. 587-595 (Academic Press, San Diego, 1985. [ Links ]

[27] L. Novotny and B. Hecht, Principle of Nano-optics, 1st ed. (Cambridge University Press, Cambridge, UK, 2006). [ Links ]

[28] WebElements, [28] WebElements, https://www.webelements.com , (last accessed September 6th, 2022). [ Links ]

[29] J. Tao, J. P. Perdew, and A. Ruzsinszky, Accurate van der Waals coefficients from density functional theory, P. Natl. Acad. Sci. (USA) 109 (2012) 18. [ Links ]

[30] T. Ooura and M. Mori, The double exponential formula for oscillatory functions over the half infinite interval, J. Comput. Appl. Math. 38 (1991) 353. [ Links ]

[31] M. Mori and M. Sugihara, The double-exponential transformation in numerical analysis, J. Comput. Appl. Math. 127 (2001) 287. [ Links ]

[32] A. D. Yaghjian, Electric dyadic Green’s functions in the source region, Proc. IEEE 68 (1980) 248. [ Links ]

[33] G. S. Agarwal, Quantum electrodynamics in the presence of dielectrics and conductors. I. Electromagnetic-field response functions and black-body fluctuations in finite geometries, Phys. Rev. A 11 (1975) 230. [ Links ]

[34] W. Eckhardt, First and second fluctuation-dissipation theorem in electromagnetic fluctuation theory, Opt. Commun. 41 (1982) 305. [ Links ]

[35] K. Joulain, J.-P. Mulet, F. Marquier, R. Carminati and J.-J. Greffet, Surface electromagnetic waves thermally excited: Radiative heat transfer, coherence properties and Casimir forces revisited in the near field, Surf. Sci. Rep. 57 (2005) 59. [ Links ]

Appendix

A. Green tensor derivation

When there is an external dipole with moment p at r0, the electric field that excites the particles is

E0(r)=k12ε0ϵ1G↔0(r,r0,ω)⋅p (A.1)

we recall that G↔0 is the Green tensor of the bulk medium (see Eq. (3)). Then, we solve the scattering problem with the dipolar excitation field Eq. (1). By using the volume integral method ^[27], it turns out that the electric field outside the particles is

E(r)=E0(r)+k12ϵ1P∫Vs(ϵs-ϵ1)G↔0(r,r',ω)⋅E(r')d3r'+k12ϵ1P∫VP(ϵp-ϵ1)G↔0(r,r',ω)⋅E(r')d3r'. (A.2)

Here, P denotes principal part and tensor G↔0 is ^[32]

G↔0(r,r',ω)=G↔0(r,r',ω)-I↔3k12δ(r-r'), (A.3)

where δ(…) is the Dirac-δ function; the last two terms of the right hand side of Eq. (2) correspond to the electric field that is scattered by each particle. As seen in (2), to obtain the electric field elsewhere outside the scatterers, we require to find the electric field inside each particle. From (2), the following equations are found

E(rp)=E0(rp)+i4πap33k136πϵ1E(rp)-ϵp-ϵ13ϵ1E(rp)+4πas33k12ϵ1(ϵs-ϵ1)G↔0(rp,rs,ω)⋅E(rs) (A.4)

E(rs)=E0(rs)+i4πas33k136πϵ1E(rs)-ϵs-ϵ13ϵ1E(rs)+4πap33k12ϵ1(ϵp-ϵ1)G↔0(rs,rp,ω)⋅E(rp) (A.5)

We mention that Eqs. (4) and (5) follow from the fact that, in the limit r→r', the real part of G↔0 is dominated by the Dirac-δ function of (3) whereas the imaginary part of G↔0 is

ImG↔0(r,r,ω)=ImG↔0(r,r,ω)=I↔k16π. (A.6)

Equations Eqs. (4) and (5) can be rearranged as

3ϵ1E0(rp)(ϵp+2ϵ1)Γp=E(rp)-4πas3k12ϵs-ϵ1(ϵp+2ϵ1)ΓpG↔0(rp,rs,ω)⋅E(rs), (A.7)

3ϵ1E0(rs)(ϵs+2ϵ1)Γs=E(rs)-4πap3k12ϵp-ϵ1(ϵs+2ϵ1)ΓsG↔0(rs,rp,ω)⋅E(rp). (A.8)

In Eq. (7), we solve for E(rp) and then it is substituted in Eq. (8), obtaining that the electric field inside the particle located at rs can be found by solving

Ei(rs)-k14αp(ω)αs(ω)(ε0ϵ1)2G0il(rs,rp,ω)G0lj(rp,rs,ω)Ej(rs)=3ϵ1(ϵs+2ϵ1)ΓsE0i(rs)+k12αp(ω)ε0ϵ1G0ij(rs,rp,ω)E0j(rp), (A.9)

i,j,l=x,y,z and this notation of indices is used for the remaining parts of the derivation; αp(ω) and αs(ω) have been already defined in Eq. (4). By using a similar procedure, the internal electric field inside of the particle placed at rp can be obtained by solving E(rs) from Eq. (8) and then substituting this result into (7), leading to

Ei(rp)-k14αp(ω)αs(ω)(ε0ϵ1)2G0il(rp,rs,ω)G0lj(rs,rp,ω)Ej(rp)=3ϵ1(ϵp+2ϵ1)ΓpE0i(rp)+k12αs(ω)ε0ϵ1G0ij(rp,rs,ω)E0j(rs) (A.10)

Without loss of generality, we consider that rp=0 and rs=dnz (d>0). By using the fact that

G0ij(dnz,0,ω)=G0ij(0,dnz,ω)=δ~ijk1ξi(k1d)4π, (A.11)

the electric fields inside the particles are

Ei(dnz)=3ϵ1(ϵs+2ϵ1)Γsβi(kd)k12ε0ϵ1G0ij(dnz,r0,ω)+k134πε0ϵ1αp(ω)ξi(k1d)G0ij(0,r0,ω)pj (A.12)

Ei(0)=3ϵ1(ϵp+2ϵ1)Γpβi(k1d)k12ε0ϵ1G0ij(0,r0,ω)+k134πε0ϵ1αs(ω)ξi(k1d)G0ij(dnz,r0,ω)pj (A.13)

we mention that the explicit factors ξi(k1d) and βi(k1d) are found in Eqs. (7)-(9). By substituting Eqs. (12) and (13) into (2), the electric field can written as Eq. (1) where the Green tensor is expressed as Eq. (2).

B. Force derivation

Any Cartesian component of the electric field Ei(r,t) can be decomposed in terms of its spectral Ei(r,ω) content as

Ei(r,t)=∫0∞Ei(r,ω)exp(-iωt)dω+∫0∞Ei*(r,ω)exp(iωt)dω (B.1)

Thus, the average between two signals is

〈Ei(r,t)Ej(r',t)〉=∬0‍〈Ei*(r,ω')Ej(r',ω)〉expi(ω'-ω)tdωdω'+∬0‍〈Ei(r,ω')Ej*(r',ω)〉exp-i(ω'-ω)tdωdω' (B.2)

According to the fluctuation-dissipation theorem ^[33, ^34]

〈Ei*(r,ω')Ej(r',ω)〉=WijE(r,r',ω)Θ(ω,T)δ(ω-ω') (B.3)

〈Ei(r,ω')Ej*(r',ω)〉=WijE(r,r',ω){1+Θ(ω,T)}δ(ω-ω') (B.4)

where

WijE(r,r',ω)=ℏω2πε0c2ImGij(r,r',ω) (B.5)

Notice that the vacuum and thermal correlations of the electric field depend on the Green tensor Eq. (2), that is, the electric response due to an electric dipole Eq. (1). Thus,

〈Ei(r,t)Ej(r',t)〉=2∫0∞WijE(r,r',ω){1/2+Θ(ω,T)}dω (B.6)

A similar procedure for the magnetic fields yields

〈Hi(r,t)Hj(r',t)〉=2∫0∞WijH(r,r',ω){1/2+Θ(ω,T)}dω (B.7)

Here,

WijH(r,r',ω)=ℏπμ0ImGij(r,r',ω) (B.8)

where Gij is the magnetic Green tensor, namely, the magnetic response due to a magnetic dipole. However, the magnetic Green tensor can be related to electric Green tensor by ^[35]

G↔(r,r',ω)=∇×∇'×G↔T(r,r',ω)T, (B.9)

(T denotes transpose). Hence, the spectral vacuum and thermal correlations of the magnetic field are now related to such a magnetic response as

〈Hi*(r,ω')Hj(r',ω)〉=WijH(r,r',ω)Θ(ω,T)δ(ω-ω') (B.10)

〈Hi(r,ω')Hj*(r',ω)〉=WijH(r,r',ω){1+Θ(ω,T)}δ(ω-ω') (B.11)

From (6) and (7), the elements of Maxwell-stress tensor can be found, and the force (10) becomes

Fz=∑ν=E,H‍2b2(ε0δ~νE+μ0δ~νH)∫0∞∫0π∫02π{Wxzν(rc,rc,ω)sin2θcosϕ+Wyzν(rc,rc,ω)sin2θsinϕ+Wzzν(rc,rc,ω)-Wxxν(rc,rc,ω)-Wyyν(rc,rc,ω)sinθcosθ/2}dϕdθ1/2+Θ(ω,T)dω. (B.12)

By using the explicit expression of the Green tensor (2), after a laborious algebraic manipulation, (12) becomes (12).

Received: October 11, 2022; Accepted: January 20, 2023

This is an open-access article distributed under the terms of the Creative Commons Attribution License