1 Introduction

A closed or conservative system evolves according to a Hermitian Hamiltonian in contrast with open or non conservative systems which are described by non-Hermitian Hamiltonians. There is a special class of non-Hermitian systems in which the energy exchange between the system and the environment is balanced. The entire balanced system exhibits a symmetry called PT symmetry where the symbol P stands for parity and interchanges the gain and loss components of the total system and T represents the operation of time reversal and has the effect of turning a system with loss into a system with gain and viceversa ^{[1, 2, 3]}.

Non-Hermitian PT symmetric systems can exhibit a rich and unexpected behavior and have broad applications in classical and quantum physics ^{[4, 5, 6, 7]}. PT symmetric systems have been intensively studied in optics in which many intriguing phenomena haven been experimentally confirmed and has led to the development of new ways of controlling light propagation ^{[8, 9, 10, 11]}.

Recently, anti-PT (APT) symmetric systems have attracted a lot of attention because they exhibit noteworthy effects different from the PT counterpart. An APT symmetric Hamiltonian can be defined in terms of a PT symmetric Hamiltonian by H(APT)=±iH(PT), but physically it is really difficult to implement it in the laboratory since it requires the coupling between the two subsystems to be a purely imaginary value, in contrast with the PT systems which requires a real coupling. Anti-PT symmetry has been demonstrated by using dissipatively coupled atomic beams^[12], cold atoms ^[13], electrical circuits ^[14], and optical devices ^{[15, 16, 17]}. These breakthroughs have initiated the field of exploring unique APT effects. More recently, Li et al reported the experimental realization of an APT symmetric diffusive system in Ref.^[18]. The system investigated in Ref.^[18] is depicted in Fig. 1 and consists of two identical solid rings with inner and outer radius given by R and R+δR, respectively. The thickness is b. The upper ring is rotating with angular velocity ω1, while the lower ring is rotating with angular velocity ω2=-ω1. There is an interface of thickness d and thermal conductivity k _i between the two rings. The temperature distribution along the inner edges of the upper and lower rings is given by the following diffusion coupled partial differential equations

where x is the coordinate along each edge, D=k/ρc is the diffusivity, v is the tangential velocity in the inner edge of the rings, hc=h/ρcb is the rate of heat exchange coupling, ρ is the density, c is the heat capacity and h = k _i /d is a coefficient that represents the heat exchange between the two rings. Using plane wave solutions, i.e. Ti=Aiei(κx-ωt), the system given in Eq. (1) can be cast into an APT symmetric Hamiltonian given by

where κ is the wave number and ω are the eigenvalues of the APT Hamiltonian which are given by

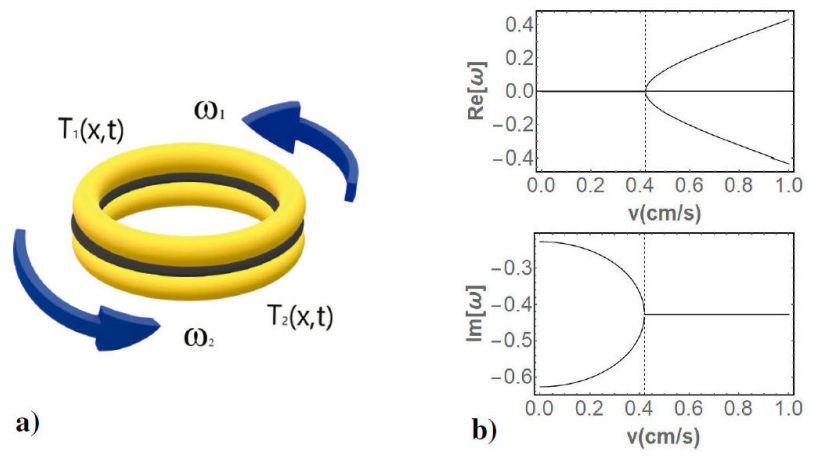
Figure 1 The figure a) shows two identical rotating rings with equal but opposite angular velocities joined together by a stationary intermediate layer and b) the imaginary and real parts of the eigenfrequencies as a function of the tangential velocity where the dotted line represents the exceptional point vEP=hc/κ.  

The exceptional point where the two eigenvectors coalesce is when vEP2=hc2/κ2, i.e. ω+=ω-. The sudden collapse of the eigenvectors and eigenvalues at the exceptional point leads to an abrupt reduction in dimensionality, i.e. the Hamiltonian matrix cannot be expressed in a diagonal form. Many of the interesting properties of non-Hermitian systems are found at or close to the exceptional point which have led to many novel and exotic phenomena. Exceptional points are currently the subject of many interesting and counter-intuitive phenomena associated with them such as topological mode switching ^{[19, 20]}, reflection and transmission ^{[21, 22, 23]}, instrinsic single-mode lasing ^{[24, 25]} and coherent perfect absorption ^[26].

In this work we study the APT symmetric diffusive system given by Eq. (1) when v=vEP and show that the system behaves as a pair of coupled linear oscillators one with gain and the other one with loss. The noteworthy feature of the exceptional point vEP is that it exhibits damped Rabi oscillations in the unbroken PT phase transition that depends on the radii of the rotating rings. We obtain the analytical temperature distribution of each ring at the exceptional point and obtain the conditions that have to be fulfill in order for the system to be in equilibrium.

2 Analysis at the exceptional point

We start our investigation by making the following change of variables in Eq. (1): τ=hct, z=hc(λ-1)/Dx where λ>1 is an auxiliary constant to be determined and ΔTi=Ti-T0 where T ₀ is a reference temperature. Rewriting Eq. (1) in terms of the new variables we have

Looking for solutions of the form ΔTi=e-λτfi(z) in Eq. (4) we end up with the following system of coupled ordinary differential equations

Inspection of Eqs. (5) reveals that they are invariant under combined parity, i.e. f1↔f2, and time reversal t→-t transformation. To solve the system of equations analytically we first differentiate one of the equations and then use the other equation to eliminate f₂ in order to get the following fourth order differential equation

where ϵ=1/(λ-1). By assuming a solution of the form f1(z)∝cosh(χz) for Eq. (6) we get the following condition over χ:

where a2=ϵvEP2/Dhc. The solution of Eq. (7) is given by

In order to have an oscillatory behavior we must demand that χ2<0, which implies that

Condition (ii) gives ϵ<1 and condition (i) gives

If ϵ<1 and a<acrit we get the following oscillatory solution for f₁

where χ1,2=|χ±2| and A₁ and B₁ are constants to be determined. In order to obtain the value of ϵ we must consider the periodicty of f1(z), i.e. f(0)=f(2πRhc/Dϵ), which gives us the following conditions

where n=±1,±2,…. Solving Eq. (11) we get the following value for ϵ

Using the fact that ϵ=1/(λ-1) we get the following value for λ

Equation (13) is in agreement with Eq. (3) when vEP2=hc2/κ2 and k = n/R. Interestingly, Eq. (13) is valid only when conditions (i) and (ii) are fulfilled.

Once we know the value of ϵ we can substitute in a2=ϵvEP2/Dhc in order to get a=ϵ. Substituting this value into Eq. (9), the conditions to be satisfied in order to have unbroken-PT symmetry at the exceptional point are 0<ϵ<1 and 0<ϵ<2(1-1-ϵ2), which gives us the following solution

Equation (14) is the main result of this study which states that two phase transitions take place at the exceptional point and depend only on the radii of the rotating rings. Substituting a=ϵ in Eq. (8) we get χ+2=ϵ2-1 and χ-2=-1, therefore f1(z)=A1cos(1-ϵ2z)+B1cos(z) which means we have to choose A₁ = 0 in order to fulfill the periodicity condition. Substituting f₁ into Eq. (5) we obtain the following ordinary differential equation for f₁:

The general solution for Eq. (15) is given by

where A₂, B₁, ϕ and n are constants to be determined by the initial conditions.

If we impose the following initial conditions over the temperature profiles in the rings

we need to choose n = 1 and B₁ = A in order to get

and

where α=1-(hcR2/2D)2 and

The solution given in Eq. (18) means that ΔT1(x,0)=f1(x), therefore the temperature distribution in the first ring will not change in position but will only decay on time, in contrast with the solution given in Eq. (19) which is different from the initial condition, therefore the temperature profile will change in position and decay on time. In Fig. 2 we show the Rabi oscillations as a function of position for different values of ϵ.

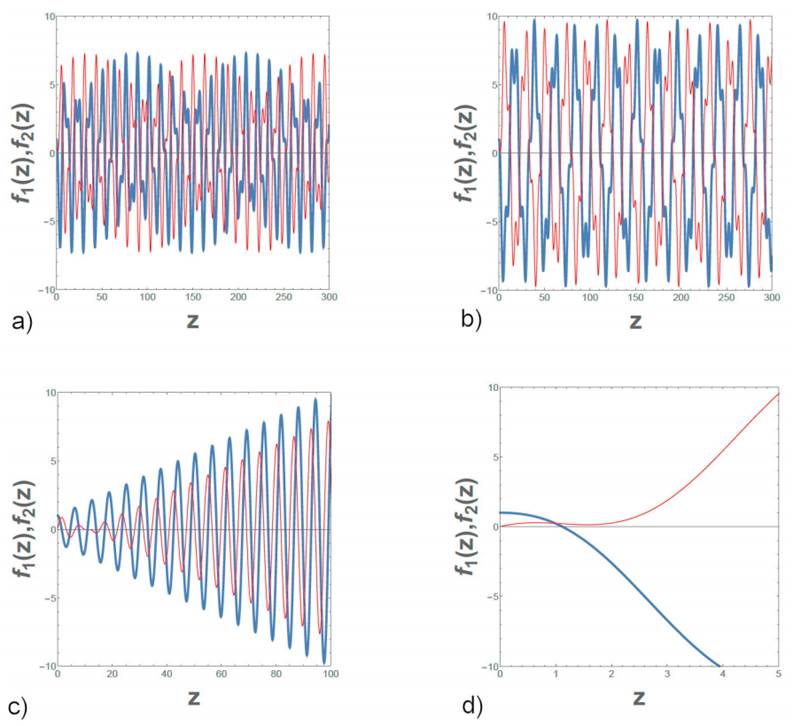
Figure 2 Numerical solution of the coupled equations given in Eq. (5). The initial values are f1(0)=1, f2(0)=0, f1'(0)=0 and f2'(0)=1. Plots are shown for different values of the ϵ: a) ϵ=0.86 and b) ϵ=0.96 presents the numerical solution in the region of unbroken PT symmetry, respectively. c) ϵ=0.09 and d) ϵ=1.1 in the broken PT symmetry, respectively. The behavior in the broken and unbroken regimes are qualitatively different. In the unbroken regime case the envelopes of the solutions exhibit oscillations, i.e. Rabi oscillations. In the broken regime case the solutions oscillate and grow exponentially.  

If we impose the following new conditions over the temperature profiles in the rings

we need to choose n = 1, B₁ = -A, A₂ = 0, which means that ΔTi(x,0)=fi(x), therefore both temperature distributions will remain invariant and will only decay on time.

Using the same experimental values given in Ref. ^[18], i.e. D = 100 mm²/s, ρ=1000 Kg/m³, c = 1000 J/Kg°K, k _i = 1 W/m°K, a = 100 mm, b = 5 mm and d = 1 mm, we find that Rabi oscillations take place for the fundamental wave if the inner ring radius is between 20mm<R<22mm and the rings are rotating with equal but opposite velocities given by vEP=hcR. In Fig. 3 we show the temperature fields for the unbroken-PT regime where damped Rabi oscillations occur in which the maximum and minimum temperatures are 90° out of phase.

Figure 3 The graph shows the temperature profiles of the rings for the following values D = 100 mm ²/s, ρ=1000 Kg/m³, c = 1000 J/Kg°K, k _i = 1 W/m °K, a = 100 mm, b = 5 mm, d = 1 mm and for the radii R = 21 mm and vEP=4.2 mm/s.  

3 Conclusions

In conclusion, we have predicted the existence of Rabi oscillations at the exceptional point in the diffusive system proposed by Li et al. We showed that at the exceptional point the system exhibits two PT phase transitions which take place at critical values for the radii of the rotating rings. Specifically, if the rings are rotating in opposite directions with equal tangential velocity given by vEP=hc/|κ| and the ring radius lies between 4D/5hc<R<D/hc for the fundamental wave, i.e. κ=±1/R, the temperature fields exhibit damped Rabi oscillations.

Let us now consider the case when the rings are rotating with different velocities close to the exceptional point, specifically we would like to solve the following system

where δv<<vEP. At first it seems that the system given in Eq. (22) is not APT symmetric, however if we make the following transformation ξ=x-δvt we obtain a system of equations identical to the one given in Eq. (1) replacing x→ξ and v→vEP. The solution for Eq. (22) is given by

which means that the temperature profiles are moving. This result shows that we can have a rest-to-motion temperature profile without having equal opposite rotating velocities. Our work reveals the rich structure of exceptional points in anti-parity-time symmetric diffusive systems.