1 Introduction
Using magnetic particles as building blocks to construct more complex structures is a well known approach to fabricate materials with tailored magnetic properties. A well developed and extensively studied class of such materials are the so-called soft magnetic composites[1], in which magnetic powders of a soft magnetic material are compacted to form a larger, macroscopic shape. These materials are very interesting for their application as soft materials [2, 3]. Such constructions using densely packed particles has also been explored with magnetic nanoparticles [4, 5, 6]. Another interesting example was reported by Merk, et al.[7], where they found that using wood as a template, an anisotropic composite material is obtained, related to the hierarchical structure of wood. In another report, magnetic particles have been printed using an inkjet printer leading to an anisotropic printed material [8]. These reports show that when particles are packed in a given geometry, the assembly tends to show a magnetic anisotropy having the symmetry of the enveloping volume [9, 10]. Interestingly, this has been observed when nearly spherical isotropic particles are packed together. This anisotropy is due to magnetostatic effects, in particular demagnetizing dipolar interaction between the particles. Moreover, there is evidence showing that changing the shape of the particle packing and forming arrays of such packings can lead to novel anisotropy properties which show symmetry properties derived from both the shape of the packing and the array formed with them [4, 5, 7, 8, 11].
Calculation of the magnetic anisotropy properties of these systems is complex and requires specialized software and computing resources [12]. In this sense, simple model calculations capable of providing a clear and practical view of the relation between the packing geometries and the resulting magnetic properties are needed. Specially given the current progress of current fabrication techniques that provide an unprecedented control at the nanoscale to produce extremely complex particle assemblies. In this sense, herein we propose and validate a simple mean-field model for spherical particle assemblies which accounts for the magnetostatic properties of these systems. These properties allow to obtain the magnetic shape anisotropy of the assembly. Moreover, we focus our analysis to cylinder shaped assemblies of packed spherical particles. The cylindrical shape includes the tube (hollow cylinder) and the homogeneous cylinder. For both cases, it is possible to use approximate expressions for the demagnetizing factors leading to simple analytical expressions. The model is extended to include the more complex case of a two dimensional array of cylinder shaped assemblies of packed spherical particles. The results show that despite using spherical isotropic particles, the assembly shows an effective magnetic anisotropy that originates in the dipolar interaction between the magnetized particles. The symmetry and magnitude of this anisotropy depends explicitly on the geometrical parameters of the system.
Overall, the model is shown to lead to the expected limiting cases without any inconsistency. Moreover, we show that it allows to vary independently all the relevant parameters of the system. The results provide insight into the role played by each parameter and sheds light to possible mechanisms viable to control and tailor the magnetic anisotropy of these particle assemblies.
2 Model for cylinder shaped assemblies of packed spherical particles
When forming a cylindrical packing of particles, we consider two main geometries: a homogeneous circular cylinder and the hollow circular cylinder, or tube, as the ones depicted schematically in Fig. 1a). In the following we assume that the long axis is along the z-axis. For the cylindrical packing we have the following parameters: cylinder diameter
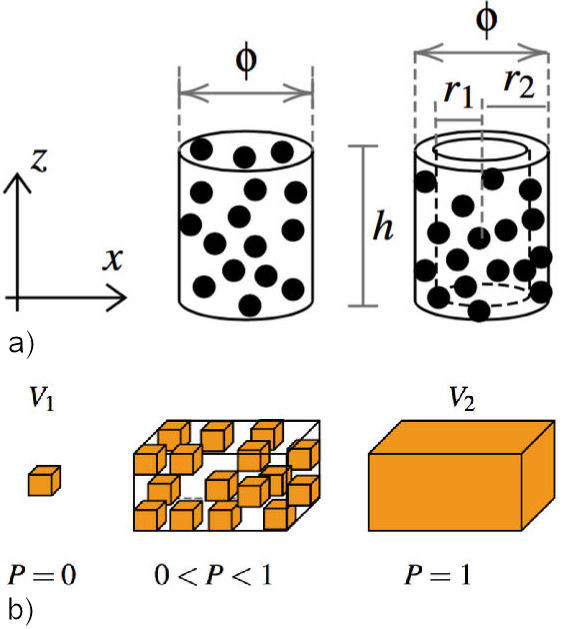
Figure 1 a) Two cylindrical packing of particles, a homogeneous cylinder and a tube, along with their main geometrical parameters. b) Particle assembly starting from the single isolated particle corresponding to a zero packing fraction, intermediate packing fractions and the completely filled volume P = 1.
To describe the magnetostatic effects of these systems we use the formulation of the effective demagnetizing field for particle assemblies reported by Martínez-Huerta, et al.[13]. The model considers the assembly as a collection of identical particles contained in a bounding outer volume as ilustrated in 1b). This particle is the elemental building block and it is characterized by its volume
This expression corresponds to the sum of the demagnetizing effects of the single elementary particle, namely the first term N
1, and the effects of the interaction between particles which are bounded by the external volume occupying a volume fraction P, which is the second term
Using these effective demagnetizing factors, the total magnetostatic or shape anisotropy can be determined. To this end, we recall that the shape anisotropy is defined as
Using Eq. (1) to calculate
This expression is proportional to the anisotropy energy
This model was used to study the particular cases where the external volume was a circular cylinder as well as a tube or hollow cylinder filled with a volume fraction P with spherical particles, as shown in Fig. 1a). Then, the model was extended to treat the case of a 2D array of such parallel tubes/cylinders packing of spheres, as those shown schematically in Fig. 2.
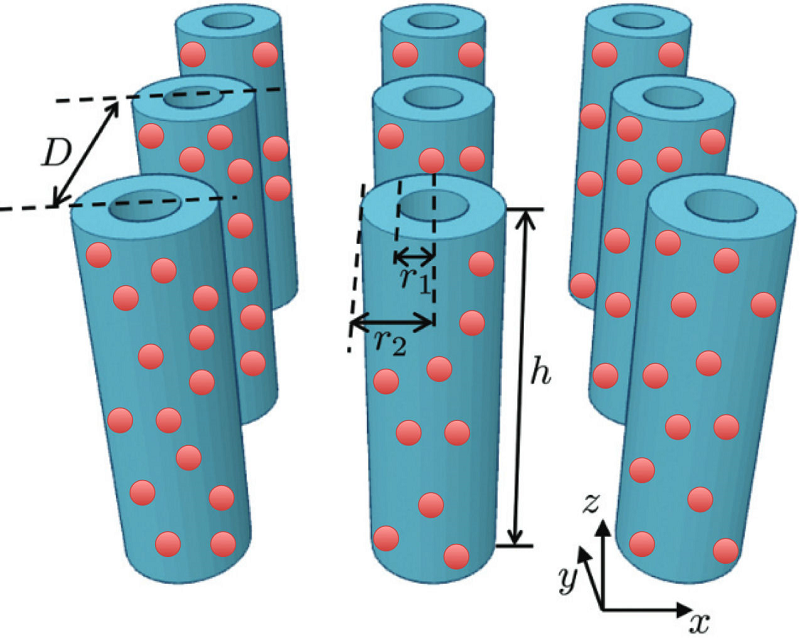
Figure 2 2D array of parallel tubes each containing spherical particles with a volume fraction P
1. The geometrical parameters of the system are the internal and external radii (
2.1 Cylinder shaped assemblies of packed spherical particles
Consider an assembly of spherical particles which have no magnetocrystalline anisotropy. The demagnetizing factor for this volume is
Since the particles are spherical,
Hereon, we drop the number 2 in the sub-index, so
While the axial demagnetizing factor of a homogeneous circular cylinder is computed as a function of the aspect ratio
Sustitution of Eqs. (4) and (5) in (3) leads to the following approximate analytical expression for the shape anisotropy of a tube containg spherical particles,
As we can see, the effective anisotropy depends on the aspect ratio of the tube,
2.2 Two dimensional array of cylinder shaped assemblies of packed spherical particles
We now extend the model for the case of a two dimensional array of cylinder shaped assemblies of packed spherical particles. This case leads to the interaction between tubes. Figure 2 shows a 2D array of parallel tubes each containing spherical particles. In this case, we have the same parameters (inner and outer radii, height) with the addition of the center-to-center distance D. For this system we have two packing fractions: P 1 corresponding to the volume fraction of the spherical particles in each tube, and a second packing fraction P 2 corresponding to the tubes in the 2D array.
This system can be described using three different volumes and their respective demagnetizing factors. As previously, the first volume is that of the spherical particles, N 1. The next volume is that of the cylindrical tube, N 2 and now we include a third volume which corresponds to a thin film, N 3, that contains the 2D array. Figure 2 depicts the system, where the same geometrical parameters are used as before with the addition of the center-to-center distance between cylinders D.
To extend the model we start with Eq. (1). Since the tubes N
2 form an array, we call
Now, for
as in the previous section, the effective anisotropy is given as
As done before, from this expression it is possible to analyze the most important limiting cases. The first one is when
The corresponding demagnetizing factors can be entered in Eq. (9). For the spheres and tubes, we use the same as before and for the thin film
Taking again
To further simplify, we use Eqs. (4) and (5) for N
z as before. For the packing fraction of the tubes in the thin film (P
2) we use the expression reported previously for a 2D hexagonal array of tubes with external diameter
Note that the first term in Eq. (10) reduces to Eq. (6). Substitution of the expressions for N z and P 2 leads to the following analytical expression for the (reduced) effective anisotropy,
This expression contains the sum of two terms and they both correspond to dipolar interaction field contributions. Comparing to Eq. (9), the first term in Eq. (12) is the dipolar interaction between the particles in a given tube. While the second term represents the dipolar interaction between tubes in the 2D array. Here again
We note that
3 Results and discussion
In the previous sections analytical approximate expressions have been obtained for the 2D array of tube shaped spherical particle arrays. These expressions can be easily evaluated making it practical and easy to obtain curves of the different quantities of interest. We analyze first the case of a single cylinder shaped assembly of packed spherical particles, and then we consider the 2D array of such cylinder shaped assemblies.
3.1 Single cylinder shaped assembly of packed spherical particles
From the expression derived in the previous sections it is possible to analyze the properties of the effective demagnetizing field and the effective shape anisotropy of the system.
As a first point, we note that the system has a finite magnetic anisotropy despite the fact that it is built using isotropic spherical particles. Indeed, despite
We can see that for
From Eq. (6) it is possible to derive some important limiting values of the effective shape anisotropy. The first important limit is for very tall tubes, this is
The case of an infinitely tall homogeneous cylinder follows when P = 1, which leads to the well known value of the shape anisotropy of
Another important property is the sign of
Analyzing Eq. (3), we can see that the sign of
To analyze this in more detail, N
z has been calculated as a function of the aspect ratio using Eqs. (4) and (5), for different values of the tube wall thickness
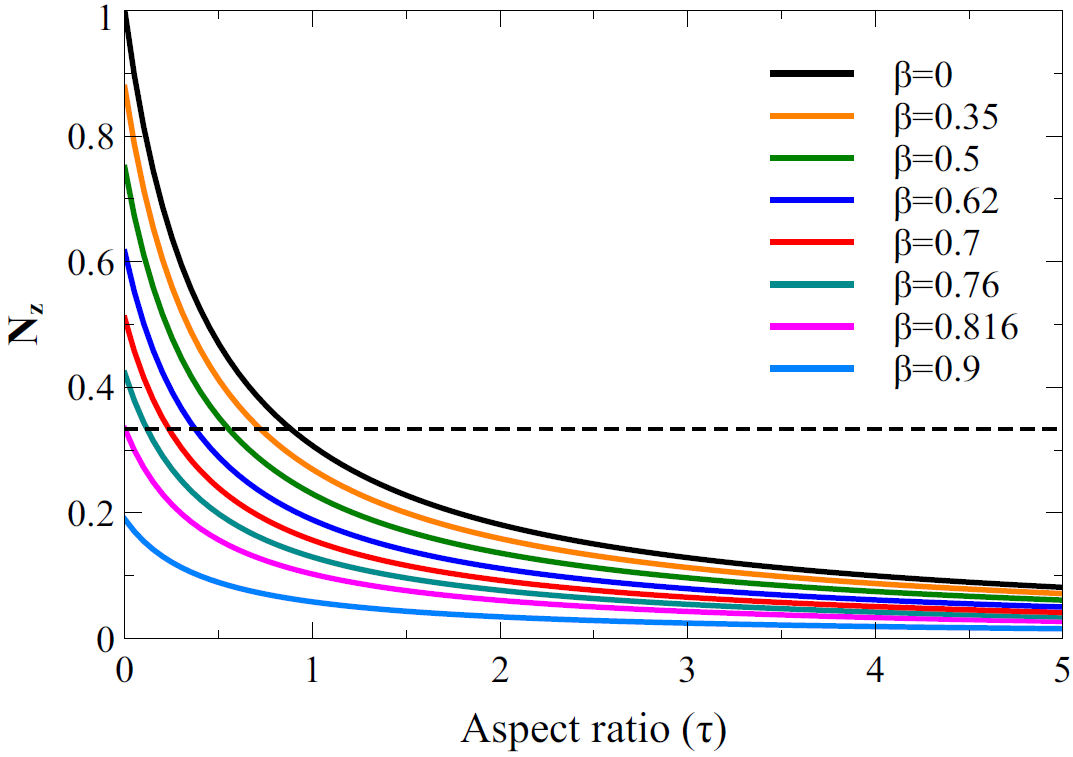
Figure 3 Axial demagnetizing factor, N
z as a function of the aspect ratio
As seen in the figure, the curves show the same general variation. They reach their maximum value when
Besides the effects of the aspect ratio and tube wall thickness on the demagnetizing factor and the resulting magnetic anisotropy, the packing fraction of the particles is another important parameter. Consider first the limiting case P = 1 and the material is a continuous and homogeneous tube (
Figure 4a) shows the reduced effective anisotropy as a function of the aspect ratio for different tube wall thickness
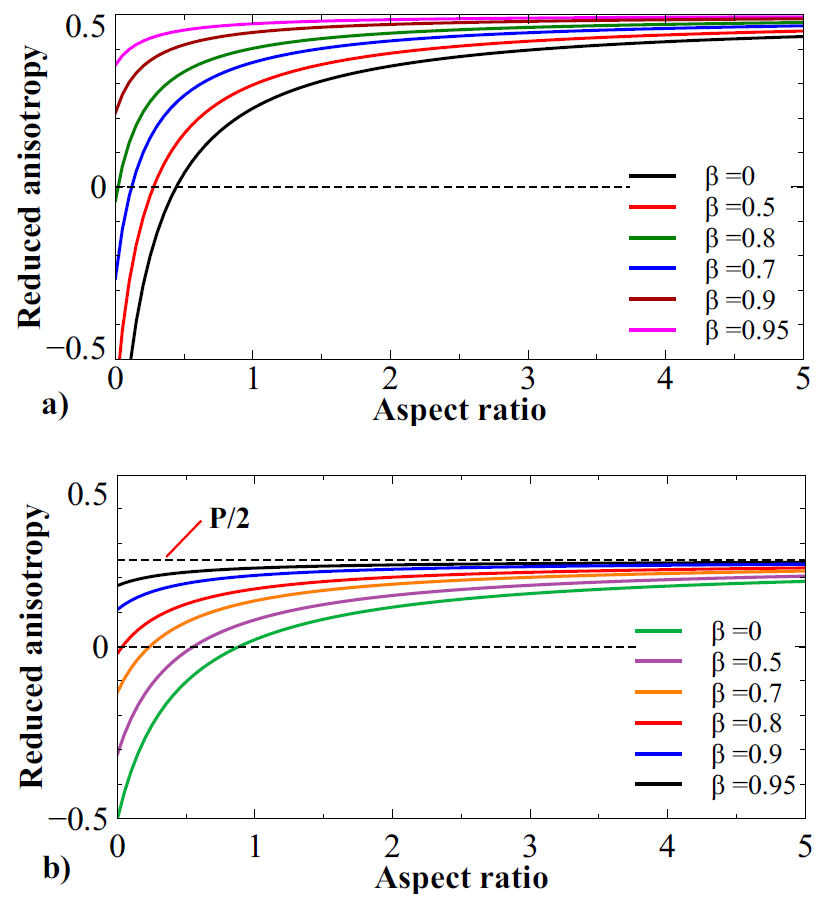
Figure 4 Reduced effective anisotropy as a function of the aspect ratio for different tube wall thickness
From the figure it can also be noted that for small values of
To gain further insight on the role of the packing fraction the effective anisotropy was calculated as a function of the aspect ratio while keeping the value of the tube wall thickness constant (
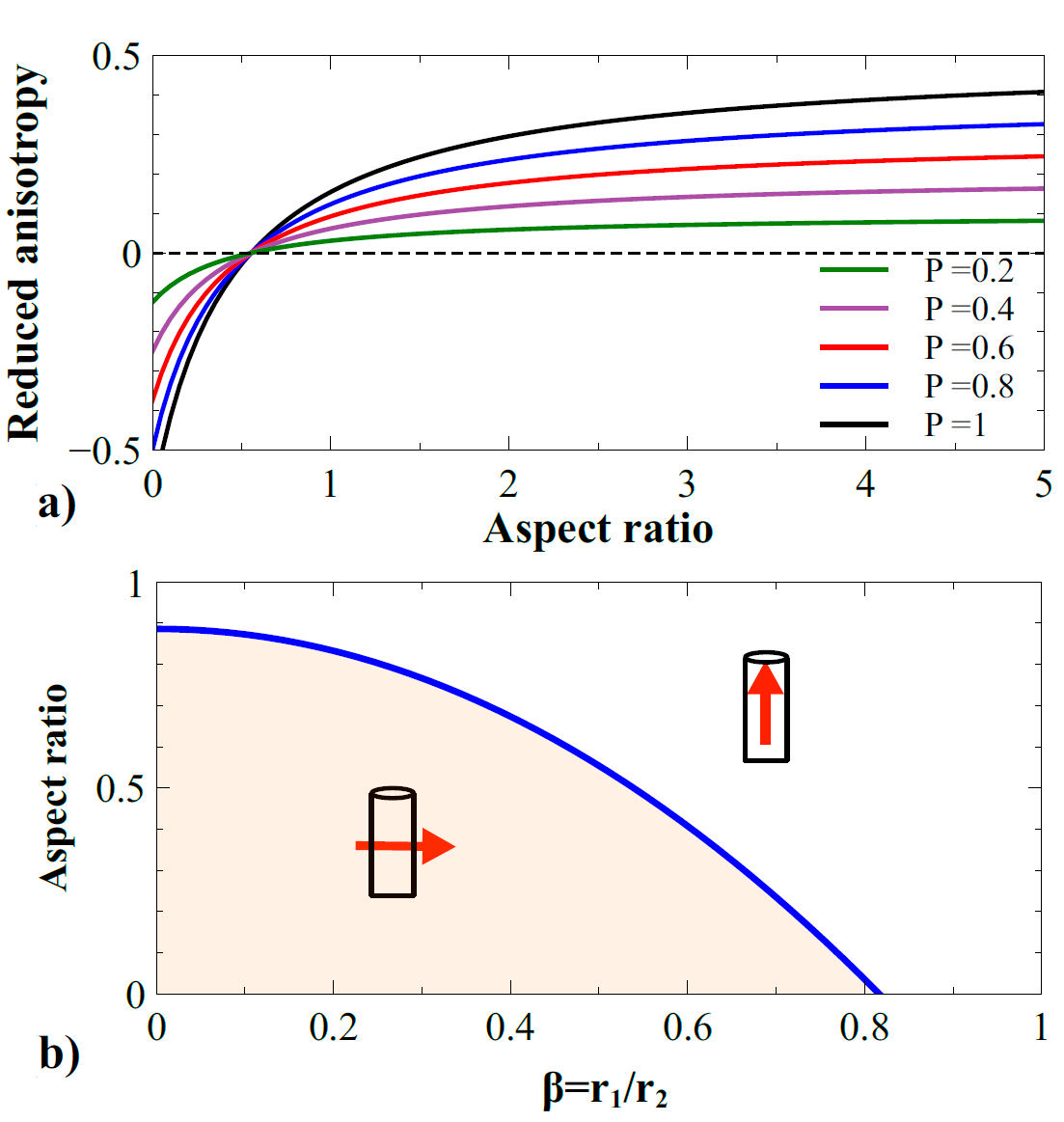
Figure 5. a) Reduced effective anisotropy as a function of the aspect ratio for different values of the packing fraction P for the particular case of
To find the condition for the isotropic point, we equate Eq. (6) to zero an solve to find the critical aspect ratio
This expression is equal to Eq. (13) in [19] which reflects a quadratic dependence on
This condition related to the tube wall thickness (
3.2 2D array of cylinder shaped assembly of packed spherical particles
In contrast to the single tube/cylinder, the 2D array introduces additional contributions to the effective anisotropy which originate in the classical dipolar interaction between the tubes/cylinders.
Equation Eq. (12) shows the sum of two terms. The first one is the interaction between spherical particles in a given tube. This is the case already analyzed in the previous section. The second term is the dipolar interaction between tubes in the 2D array. The second term is always negative which indicates that this interaction term favors an easy anisotropy axis perpendicular to the tube axis, or in the xy-plane. The amplitud of this term is modulated by both packing fractions: P 1 of the particles in the tube and P 2 volume occupied by the tubes in the thin film containing the 2D array.
To analyze the behavior and the effects of this second term, we have calculated separately the values of this term alone as well as the total anisotropy, Eq. (12). For this calculation, the tube aspect ratio was kept constant at a value of
The results are plotted as a function of the inverse of the reduced distance, this is 1/d since it is more practical. Indeed, it varies between [ 0,1], the value 1/d = 0 corresponds to the case were the tube and infinitely apart and the interaction goes to zero. Inversely, when 1/d = 1 corresponds to the limiting case where the tubes touch and its the smallest possible distance between them.
Figure 6a) and b) show the reduced interaction field, (c) and (d) the reduced anisotropy as a function of the inverse reduced distance (1/d) for different values of the tube wall thickness
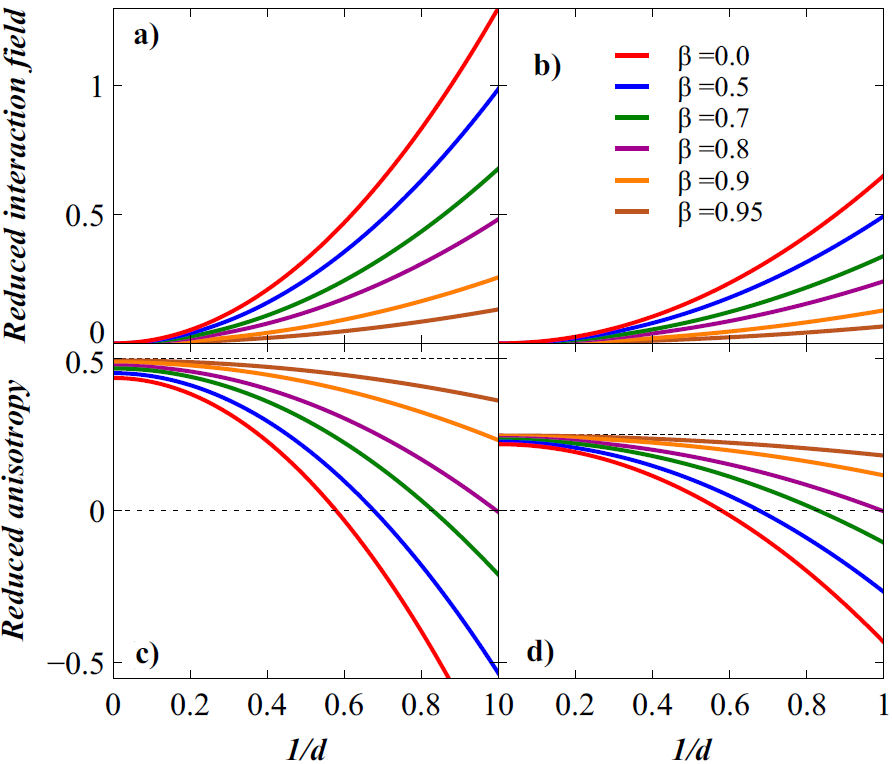
Figure 6 a) and b) Reduced interaction field, c) and d) reduced anisotropy as a function of the inverse reduced distance 1/d for different values of the tube wall thickness
For the interaction field between the tubes in the 2D array, Fig. 6a), it goes to zero when the tubes are separated (
As pointed out before, the amplitude of both terms in Eq. (12) is modulated by the factor
Regarding the effective magnetic anisotropy, this is shown in Fig. 6c) and d). The overall behavior reflects the sum of the shape anisotropy, the first term in Eq. (12), and the dipolar interaction between tubes, second term in Eq. (12), which is preceded by a negative sign. As seen in the figure, the total anisotropy is maximal when the tubes are apart, 1/d = 0, and as the distance between them is reduced, the interaction between them (with its negative sign) leads to a reduction of the total anisotropy, leading to a change in sign for certain values of
As mentioned before, the amplitude of the effective anisotropy is proportional to the packing fraction of the spheres
As already mentioned, the packing fraction of the particles in the tube
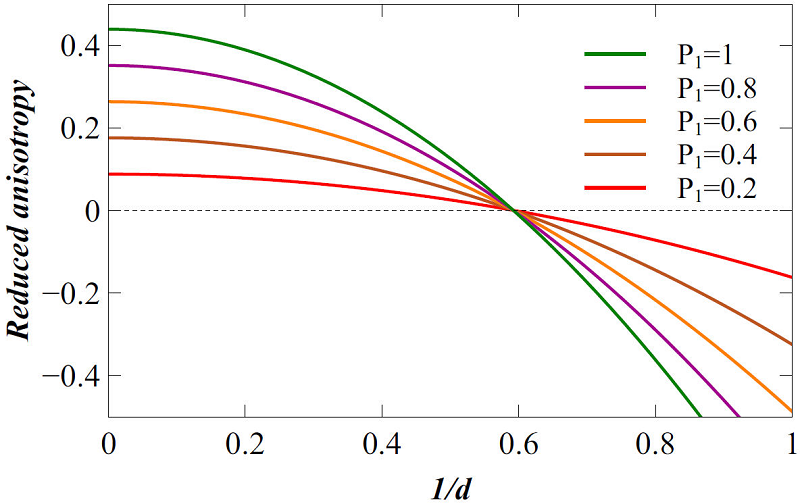
Figure 7 Reduced anisotropy as a function of the inverse of the reduced distance for different packing fractions of the spherical particles in the tubes P
1 with constant tube aspect ratio
As observed for the case of a single tube, the effective anisotropy shows a change of sign, as seen in Fig. 6c), d) and Fig. 7. However, this does not happen above certain values of
This expression shows that the critical aspect ratio (
Equation Eq. (16) allows calculating the zero anisotropy curves for the tube aspect ratio (

Figure 8 Isotropic curves for the tube aspect ratio
As we can see, each value of
A final remark is that Eq. (16) for the 2D array of tubes made of spherical particles is the same as equation Eq. (17) in [19] for the case of continuous tubes. This despite of being different systems. However, the case reported in [19] is obtained as a particular case of Eq. (12) when P 1 = 1. In this sense, the main reason why the same expression is obtained is that the spherical particles are isotropic and therefore they do not contribute to the shape anisotropy. Indeed, as seen from Eqs. (10) and (12), the only variable related to the spherical particles present in the effective anisotropy is their packing fraction P 1 which, as discussed above, only modulates the magnitude of the anisotropy without changing its behaviour.
To validate the model, we analyze selected experimental reports based on systems with affine geometrical features. The first case of interest is that of individual magnetic particles packed into, or confined to, a well defined geometry where the dipolar interaction between particles leads to an observable magnetic anisotropy. In these regards, there are two notable examples, the first one involves packing magnetic nanoparticles into cylinders, ideally as shown schematically in Fig. 1a). In a report, Pal, et al.[20], filled carbon nanotubes with small magnetic nanoparticles. In another report, Duong, et al.[5], filled cylindrical nano holes made in a polyacrylinitrile substrate with magnetite nanoparticles. In these two studies, the magnetic characterization showed an increase of both remanence and coercive field in the cylindrically confined particles with respect to the non-confined particles. This is an indication of the presence of a magnetic anisotropy. In both cases, these effects are attributed to the enhancement of the dipolar interaction between the confined particles. The other example is the work of Merk et al.[7], and Segmehl, et al.[21], who have performed the synthesis of magnetic nanoparticles within the hierarchical structure of wood. This structure is highly anisotropic with a predominant cylindrical structure as building block, similar to an array of pores aligned parallel to each other. The in-situ growth of nanoparticles from liquid solutions leads to an important fraction of the particles being fixed on the walls of the pores, leading to a tubular structure. This corresponds approximately to the situation depicted in Fig. 1a). In both studies, the analysis of the magnetic properties of the magnetic wood shows a magnetic anisotropy favoring an easy axis parallel to the symmetry axis of the tubes. This anisotropy is attributed to the dipolar interaction between particles that are confined to the tubular shape. In the context of our model, this follows from either Eqs. (3) or (6), where it is clear that a finite magnetostatic anisotropy arises from the dipolar interaction between the particles. Moreover, from Eq. (3) we see that the magnitude of the resulting anisotropy is a function of the cylinder aspect ratio N z and the packing fraction P of the particles. For the more complex case of analyzing the inter-cylinder dipolar interaction, these studies do not explore experimentally these effects, although they recognize its importance.
The model is also well suited for 2D arrays of magnetic nanowires grown by electrodeposition into nanoporous templates. These are 2D arrays of circular cylinders, arranged so that their long exes are parallel to each other and distributed spatially forming a film. In this case, the geometrical features are the circular cylinder and the thin film containing the 2D array. For this system, Eq. (12) needs to be simplified by taking P
1 = 1 corresponding to ideal case of a continuous magnetic material and then, to treat the case of a homogeneous cylinder, we need to take
This expression shows the competition between two terms: (a) the shape anisotropy which favors an easy axis parallel to the wires long axis the z-axis and (b) the dipolar interaction between wires, which due to the negative sign preceding it, favors an easy axis perpendicular to the long axis of the wires. The effective anisotropy of the system, in the absence of other anisotropy contributions, is the result of this competition. In this sense, a well known effect observed in arrays of NWs is the rotation of the easy axis from parallel to perpendicular to the long axis of the wires when the dipolar interaction overcomes the shape anisotropy [22,
23]. For the case of an array of continuous cylindrical NWs, the expression defining the easy axis rotation is given by Eq. (16) for
This effect can be analyzed using the model and comparing it with reported experimental results where the easy axis is shown to rotate as a function of either the distance between wires or their aspect ratio. To this end, we have selected data for Ni [24, 25, 26] and NiFe [27] NWs in order to avoid other materials that can have other magnetic anisotropy contributions.
Figure 9a) shows the easy axis diagram as a function of the aspect ratio and the inverse of the reduced distance. The continuous curve corresponds to Eq. (16) for
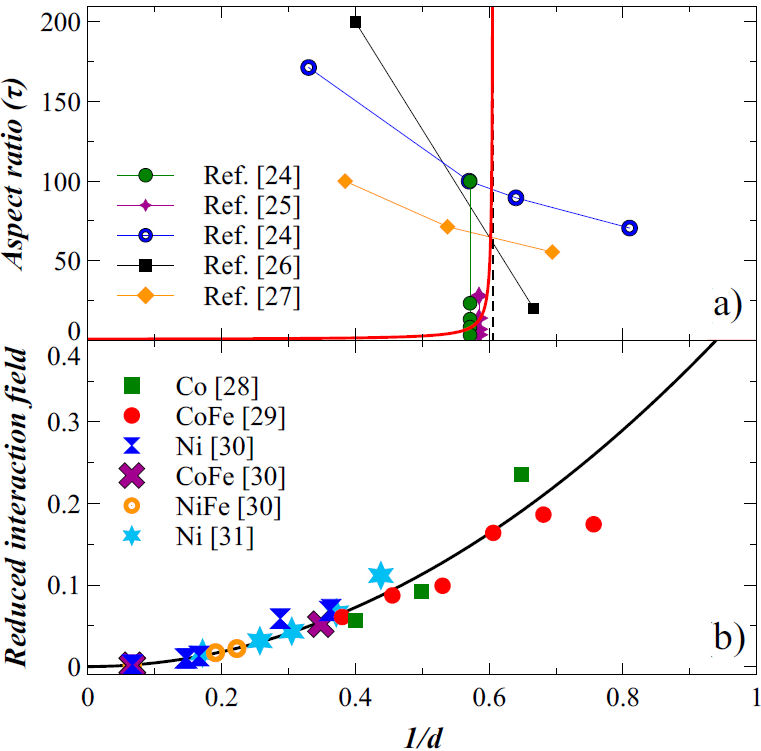
Figure 9. a) Effective anisotropy diagram for an array of nanowires as a function of the wire aspect ratio
In this diagram, the region above and to the left side of the curve, corresponds to an easy axis parallel to the long axis of the wires. The region below and to the right of the curve, corresponds to the case where the easy axis is perpendicular to the long axis of the wires.
Consider first the experimental data for the case when the aspect ratio is varied while keeping constant the distance between wires [24,
25]. As seen in the figure, the easy axis rotates from parallel to perpendicular to the cylinder axis when the aspect ratio is reduced. Moreover, as seen from the two series of data shown in the figure, the aspect ratio at which the transition takes place is lower for larger interwire distance (
The other measurements that can be compared with the model are those of the axial component of the dipolar interaction field. To compare the model with available experimental results on arrays of tall NWs, we have taken the date obtained using FORC diagrams for Co (M
S
= 1400 emu/cm3) [28] and CoFe (M
S
=1991.5 emu/cm3) [29], as well as those obtained using remanence curves in Ni (M
S
=485 emu/cm3), NiFe (M
S
=788 emu/cm3) and CoFe (M
S
=1900 emu/cm3) NWs with diameters of 71 nm and below [30]. In addition, we have extracted the data obtained from the width of the switching field distribution (SFD) for Ni NWs [31]. To obtain the value of the interaction field from the width of the SFD we assume that the reported width
The values reported in these studies correspond to the interaction term of the axial component of the interaction field [13], so to convert these values to dimensionless effective field, we have divided their magnitude by
4 Conclusions
A simple mean field model has been presented to describe magnetostatic effects in assemblies made of isotropic spherical particles. For a two dimensional array of cylinder shaped assembly of packed spherical particles we derive approximate analytical expressions for the effective magnetic anisotropy. We find that in such particle assemblies, the shapes of the volumes that contain the particles lead to a magnetic anisotropy related to the dipolar interaction despite the fact that the particles in the assembly are isotropic. We have analyzed the main limiting cases for the anisotropy of a single tubular structure containing the particles as well as the 2D array of tubular assemblies, finding for each case the expected results. Since the expressions are analytical it is simple to derive the corresponding curves of the anisotropy as a function of the geometrical parameters of the system. The results compare well with results reported in other studies.











 nueva página del texto (beta)
nueva página del texto (beta)


