Thermodynamics and statistical physics
Equation of state for solid-liquid-vapor coexistence for heavy n-alkane
F. de J. Guevara-Rodrígueza
a Instituto Mexicano del Petróleo, Eje Central Lázaro Cárdenas 152, Ciudad de México, 07730, México. e-mail: fguevara@imp.mx
ABSTRACT
An equation of state to predict solid-liquid-vapor coexistence of heavy n-alkane is developed. In this equation of state, their parameters are functions of the n-alkane molecular weight and were correlated with their corresponding values from methane 16.04 g/mol to eicosene 280.53 g/mol published in reference Chem. Eng. Commun., 209 (2022) 171; and the experimental melting temperature value of some heavy n-alkanes (from 100 g/mol until 600 g/mol).
Keywords: Solid-liquid-vapor coexistence; non-cubic equation of state; heavy n-alkane
1 Introduction
In recent papers, an Equation of State (EoS) to study the solid-liquid-vapor coexistence of a substance [1,
2,
3] was developed. The EoS is
P=R Tv-b-a(v-c)(v-d)-f T(v-e)ν,
(1a)
a=R T(b-B),
(1b)
B=b(1-(λ3-1)(eε/R T-1)),
(1c)
where P is the pressure, T is the temperature, v is the molar volume, and R is the gas constant. The function a is related to the second viral coefficient B (which is approached and derived from the square-well potential with parameters σ, ε and λ). In consequence, a depends on the interactions between molecules. Moreover, the restriction b=2πσ3/3 comes from the properties of a, namely: a is a continuous, positive (a>0), monotonically decreasing (da/dT<0), and convex (d2a/dT2>0) function of temperature [4].
A cubic equation of state[5] predicts the liquid-vapor coexistence, but the solid phase is out of scope. This limitation is corrected with the last term in Eq. (1), which is proportional to molar density, but with high power (ν=12). This term is related to very short-range molecular interactions, and therefore, its value is a very small contribution to the EoS at mid-range molecular distances, for example, at the liquid and the vapor phases. In consequence, this term does not modify the liquid-vapor coexistence practically. However, the value of this term has a relevant contribution to the EoS at high molar density. Thus, it extends the capabilities of a cubic equation of state with the solid phase inclusion.
The set of parameters S={ b, c, d, e, f, λ, ε } define the EoS of a substance, and their values are determined by using the critical point data, the acentric factor, and the temperature value at the triple point and the boiling point of the substance. After that, Eq. (1) is used to study the solid-liquid-vapor coexistence of the substance. The procedure is described and discussed elsewhere and was applied to more than a hundred substances, where the set S was determined[1,
2].
Crude oil is a complex mixture with many components that is most prevalent in it, such as aromatics, naphthenes, alkanes, and others. On the other hand, the heavy n-alkane definition starts from C
16 (hexadecane with 226.41 g/mol) and includes, for example, C
50 (pentacontane with 703.34 g/mol), and more [6]. Unfortunately, in this heavy n-alkane group, experimental data are not complete or do not exist at all. However, an ad-hoc model can be constructed from the available data and the resulting EoS is called the pseudo-alkane model. The experimental data for alkanes from C
1 (methane) to C
20 (eicosane) is available (see Ref. [1]) and was used to determine the parameter values in S.
In the literature there are also reported other equations of state, which were developed to predict the solid phase, and all of them are non-cubic EOS. Yokozeki [7,
8,
9,
10] introduce a discontinuity between the solid and the liquid region to avoid the solid-liquid critical point, but Lee [11,
12] pointed out that the EOS has a mathematical problem because there are two singularities and suggests that Yokozeki’s model should be carefully reevaluated as was recently done by Chaoping Mo, et al., [13]. Wenzel [14] modified the Peng-Robinson EoS [15] by adding a new repulsion term (like the third term in (1)), but this term does not avoid the formation of the solid-liquid critical point and introduce a temperature discontinuity at T = 0 K (by these reasons, they self-suggest to replace the added term with another instance proposed by Carnahan-Starling [16]). Later, Wenzel [17] proposed another strategy, where the Soave-Redlich-Kwong EoS [18,
19] is modified to make it applicable to the solid-liquid transition by calculating the volume change (with temperature and pressure) in the solid and liquid regions of substances. Wenzel [20] applied again the same idea by using the Peng-Robinson EoS, but in both cases, the solid phase is treated as a pure component in a pseudo-mixture [21]. However and perhaps, this work is the first effort to develop a psudo-alkane model by using a non-cubic EoS, the Eq. (1). The pseudo-alkane model is relevant to study the wax precipitation in gas condensate mixtures [22], for example. In this case, wax can precipitate before liquid condensation. If this behavior is ignored, the dew point pressure, calculated with an EoS will be incorrect. Therefore, the wax-precipitation model must predict the solid phase of the heavy n-alkanes in the mixture. Nowadays, the wax-precipitation models are extremely complex due to the number of correlation parameters [22] which are used to improve the description of the solid-state transition. On the other hand, in this work, the target is to construct a pseudo-alkane model based on Eq. (1). The pseudo-alkane model will be the keystone in a new wax-precipitation model.
The pseudo-alkane model is constructed from the EoS for C
1 to C
20 published in Ref. [1], and the experimental melting temperature value of some heavy n-alkanes. Thus, the parameters in S are functions of the n-alkane molar weight in the pseudo-alkene model. We this in mind, the manuscript is divided into four sections, namely: A brief summary of properties of the EoS to describe the solid-liquid-vapor coexistence is in Sec. 2; psuedo-alkane model is developed in Sec. 3, and the application of the new EoS to correlate the melting temperature of heavy n-alkanes is in Sec. 4. Finally, conclusions are in the last section.
2 Solid-liquid-vapor coexistence
The mechanical equation, P, is derived from the excess molar free energy,ΔA, namely:
ΔA=RTln(vv-b)+ac-dln(v-cv-d)-f T(ν-1)(v-e)ν-1,
(2)
where P and ΔA are related with
(∂ΔA∂v)n, T=RTv-P,
(3)
where n is the total number of moles of substance.
The chemical equation is other important property to determine the solid-liquid, solid-vapor, and liquid-vapor coexistence. In particular, the fugacity coefficient φ is derived from the molar variation of excess free energy, namely,
(∂∂nnΔA)V, T=RTln(Zφ),
(4)
where V=n v is the volume where the substance is confined and Z=Pv/RT is the compressibility. From Eqs. (4) and (6), the result for ln(Zφ) is
ln(Zφ)=βΔA+Z-1,
(5)
where β=1/RT. Thus, Eqs. (1), (2), and (5) constitutes the framework to study solid-liquid-vapor coexistence of pure components.
The algorithm to determine solid-liquid, solid-vapor, or liquid-vapor coexistence is discussed and showed elsewhere [1,
2]. In this point, if A and B are two phases of a substance, with A≠B, and { A, B }⊂{ Solid, Liquid, Vapor }, then both phases coexistence if they fulfill with: a) PA=PB; b) TA=TB; and c) φA=φB, but d) vA≠vB. For a temperature below to the critical value and up to the triple point value, we find a point at the melting curve with PSolid=PLiquid1 and another second point at the vaporization curve with PLiquid2=PVapor. In this case, PSolid>PVapor and the molar density of Liquid
1 phase is higher than Liquid
2 phase (i.e.vLiquid1<vLiquid2). For the triple point temperature, we find that PSolid=PLiquid1=PLiquid2=PVapor and the Liquid
1 phase is the same Liquid
2 phase (i.e.vLiquid1=vLiquid2), thus the solid-liquid-vapor coexistence (triple point) is described with Eq. (1). Finally, for a temperature below to the triple point value, we find only a point at the sublimation curve with PSolid=PVapor, where the liquid phase is an unstable state.
3 Pseudo-alkane model
The EoS in Eq. (1) was applied to some known n-alkanes from methane to heptadecane, plus eicosane and docosane (see Ref. [1]). In Table II in Ref. [1], the reader can find the parameters values in S for each n-alkane. In this work, b, c, and d are now functions of molar weight M with the following expression
b*=(c00+c01M*)c02,
(6a)
c*=(c10+c11M*)c12,
(6b)
d*=-(c20+c21M*)c22,
(6c)
where b* = b/(cm3/mol), c* = c/(cm3/mol), d* = d/(cm3/mol), and M* = M/ (g/mol). Coefficients and exponents in Eq. (6) are in the first three rows in Table I. They were computed by minimizing the mean square deviation between Eq. (6) and their corresponding value in Table II in Ref. [1], but restricted with d<0<c<b<vc, where vc is the molar volume at the critical point.
Table I Coefficients and exponents in Eq. (6), (8), and (10).
| n |
Cn0
|
Cn1
|
Cn2
|
| 0 |
18.6469 |
3.18455 |
0.863276 |
| 1 |
9.85353 |
4.56078 |
0.804816 |
| 2 |
14.4887 |
0.45967 |
1.569080 |
| 3 |
1.01175 |
9.36963 × 10-6
|
0.534545 |
| 4 |
1.01382 |
9.36963× 10-6
|
0.534545 |
| 5 |
1.83257 |
2.45633 |
0.027041 |
Table II Coefficients in Eq. (11).
| n |
C6n
|
| 0 |
-6.72779× 10-2
|
| 1 |
1.53914× 101
|
| 2 |
-7.55375× 10-2
|
| 3 |
2.03799× 10-4
|
| 4 |
-2.75580× 10-7
|
| 5 |
1.46278× 10-10
|
| 6 |
4.04943× 102
|
| 7 |
1.54841× 103
|
On the other hand, vmin and vmax are defined as an extreme molar volume at high-temperature conditions, i.e. they are related to
limT→∞(∂P∂v)n, T=0 for vmin or vmax.
(7)
Both extreme molar volume are restricted with b<vmin<vmax in order to avoid the formation of a solid-liquid critical point at any temperature. Moreover, solid phase volume is found in the range vSolid∈(b, vmin), meanwhile the liquid and vapor phase volume is found in the range vmax<vLiquid<vVapor. vmin and vmax are also functions of molar weight M with the same previous expression, namely
vmin*=(c30+c31M*)c32,
(8a)
vmax*=(c40+c41M*)c42,
(8b)
where vmin*=vmin/(cm3/mol) and vmax*=vmax/(cm3/mol). Coefficients and exponents values in Eq. (8) are in Table I in rows fourth and fifth. vmin and vmax values are used to compute the parameters e and f by using the following equations
ξ=(vmin-bvmax-b)2/(ν+1),
(9a)
e=vmin-ξvmax1-ξ,
(9b)
f=R(vmin-e)ν+1ν(vmin-b)2.
(9c)
In this way, e and f are also functions of M.
The second virial coefficient B in (1c) is derived from the square-well potential. This potential is characterized with parameters σ, λ and ε. In this case, the first parameter (i.e. the hard core diameter σ) is restricted with b=2πσ3/3 as a consequence of the properties of the function a. The second parameter λ is related to the width of square well and is correlated with the molecular weight M by using the following expression
λ=c50+c51e-c52M*,
(10)
coefficients C
50, C
51 and C
52 are in Table I (at the sixth row). Again, they were computed by minimizing the mean square deviation between Eq. (10) and its corresponding value in Table II in Ref. [1].
The last function in the pseudo-alkane model corresponds to ε which is the depth of the square well potential. This function will be developed from the correlation between the experimental melting temperature data of some heavy n-alkanes and the model predictions. The procedure is in the next section.
4 Melting point temperature
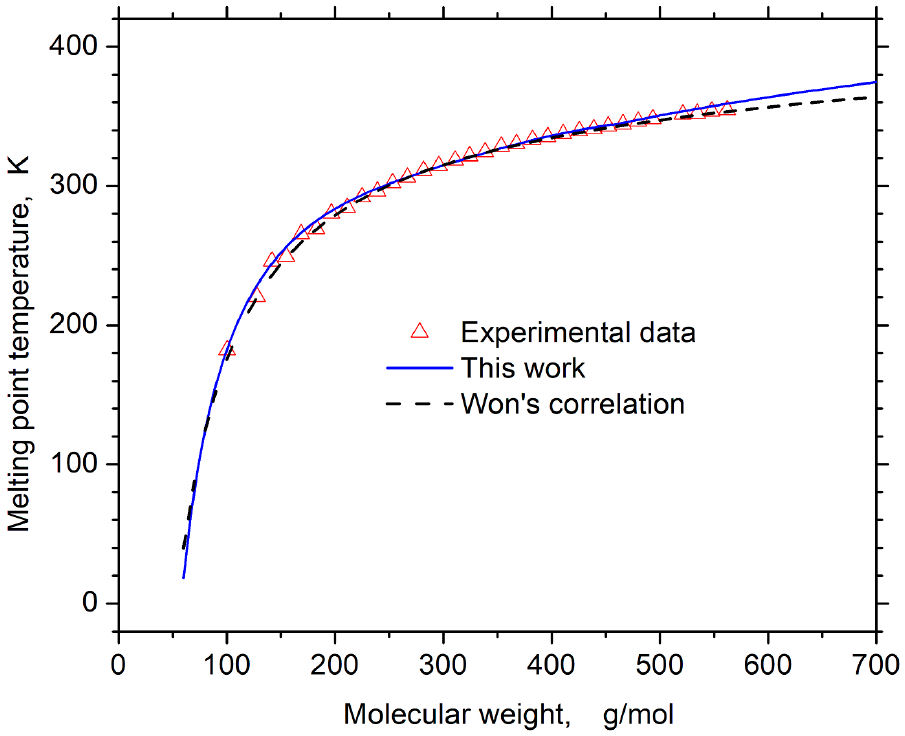
The functions of molar weight M showed in the previous 3 (except ε) were correlated with their corresponding value in Table III in Ref. [1]. Meanwhile, the mean square deviation between the melting temperature obtained with Eq. (1) and its experimental value is minimized with the function ε, for heavy n-alkanes [23]. The blue solid curve in Fig.1 is the resulting melting temperature obtained with Eq. (1), and the red symbols are the experimental data. The numerical results agree with experimental data, and the curve goes beyond both sides of experimental data because the function for ε has the following expression
(εR)*=∑n=05c6n (M*)n, if M<Mcut,c66ln(M*)-c67, if Mcut≤M,
(11)
where (ε/R)*=(ε/R)/K. The expression for ε is a piecewise function where Mcut=461.97 g/mol is the cut-off and corresponds to a continuous and soft-transition between both parts. Coefficients values are in Table I.
Table III The melting temperature data from experiment (exp) [23,
24] and pseudo-alkane model (cal).
M
g/mol |
T(exp)
K
|
T(cal)
K
|
ΔT
% |
| 100.2 |
182.1 |
182.85 |
0.41 |
| 127.8 |
220.3 |
228.54 |
3.74 |
| 141.6 |
245.8 |
244.04 |
0.71 |
| 155.0 |
249.3 |
256.23 |
2.77 |
| 168.7 |
265.5 |
266.33 |
0.31 |
| 182.8 |
268.9 |
274.99 |
2.26 |
| 196.4 |
280.2 |
281.93 |
0.61 |
| 211.3 |
284.2 |
288.38 |
1.47 |
| 224.9 |
292.1 |
293.45 |
0.46 |
| 239.0 |
296.1 |
298.16 |
0.69 |
| 253.2 |
302.0 |
302.44 |
0.14 |
| 266.7 |
305.9 |
306.20 |
0.09 |
| 281.6 |
310.9 |
310.12 |
0.25 |
| 295.8 |
314.4 |
313.69 |
0.22 |
| 310.7 |
318.4 |
317.30 |
0.34 |
| 324.2 |
321.3 |
320.47 |
0.25 |
| 338.3 |
324.3 |
323.70 |
0.18 |
| 353.2 |
328.3 |
326.97 |
0.40 |
| 367.4 |
330.3 |
329.94 |
0.10 |
| 382.3 |
333.3 |
332.89 |
0.12 |
| 396.4 |
335.3 |
335.49 |
0.05 |
| 410.6 |
337.3 |
337.88 |
0.17 |
| 425.4 |
339.4 |
340.14 |
0.21 |
| 438.9 |
340.9 |
341.95 |
0.30 |
| 452.3 |
342.9 |
343.55 |
0.18 |
| 465.8 |
344.4 |
345.33 |
0.27 |
| 479.9 |
346.4 |
347.55 |
0.33 |
| 493.4 |
348.0 |
349.58 |
0.45 |
| 521.0 |
351.5 |
353.56 |
0.58 |
| 534.4 |
352.0 |
355.40 |
0.96 |
| 547.9 |
353.6 |
357.20 |
1.01 |
| 562.0 |
354.6 |
359.03 |
1.24 |
ΔT=100×|T(cal)-T(exp)|/T(exp)
The melting temperature values from the experiment and pseudo-alkane model are in the second and third columns in Table III, respectively. The percent deviation is in the fourth column, and their values have a normal distribution with the following mean deviation: ( 0.67±0.47 )%. Therefore, the model predicts the melting temperature as a function of molar weight at least in the range (100, 600) g/mol.
In 1986, Won [24] proposed a solid-liquid-vapor equilibria model for paraffinic hydrocarbon mixtures. In this model, solid-liquid equilibria is determined through activity coefficient of liquid phase, meanwhile, the liquid-vapor equilibria is determined by using the SRK-EOS [18,
19]. Additional, Won proposed a empirical correlation for the temperature of melting points. In this case, the correlation equation is
Tm*=374.5+0.02617 M*-20172/M*,
(12)
where Tm*≡T/K. The results from the about the temperature correlation of melting points are plotted in Fig. 1 with the black dashed curve. The correlation equation describe the experimental data as well as the predictions obtained with the pseudo-alkane model in this work.
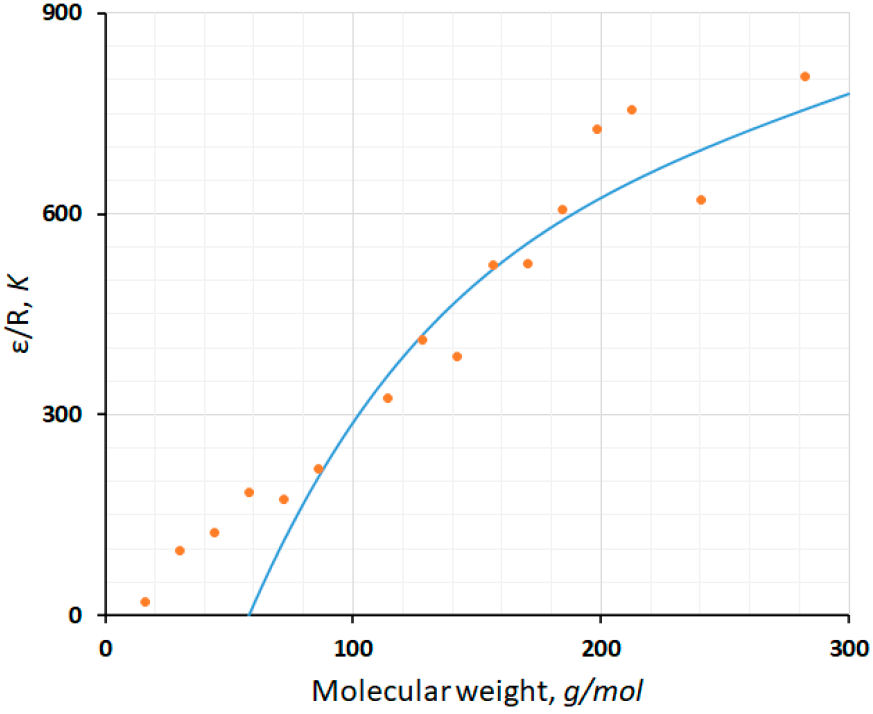
On the other hand, the pseudo-alkane model was developed by using the melting temperature of heavy n-alkanes and does not work for methane (16.04 g/mol). In this case, ε has an unphysical value through Eq. (11). To clarify this point, the ε values published in Ref. [1] are shown in Fig. 2 with symbols and the curve corresponds to Eq. (11). The curve passes through the points but has a deviation of more than 30% for butane and pentane cases. In fact, Eq. (11) has a root at M=57.64 g/mol, and therefore, methane, ethane, and propane are excluded. In consequence, the pseudo-alkane model works starting from hexane (86.17 g/mol).
Table IV The melting temperature data from Eq. (1) at Ref. [1] and pseudo-alkane model (cal).
| |
M
g/mol |
T(exp)
K
|
T(cal)
K
|
ΔT
% |
ε/R
K
|
ε(cal) /R
K
|
Δε
% |
| methane |
16.04 |
0.0 |
- |
- |
21.273 |
- |
- |
| ethane |
30.07 |
0.0 |
- |
- |
97.102 |
- |
- |
| propane |
44.10 |
0.0 |
- |
- |
124.30 |
- |
- |
| butane |
58.12 |
134.61 |
3.4762 |
97.41 |
183.36 |
3.5905 |
98.04 |
| pentane |
72.14 |
143.48 |
91.654 |
36.12 |
173.11 |
113.84 |
34.23 |
| hexane |
86.17 |
177.84 |
146.12 |
17.83 |
219.94 |
208.54 |
5.183 |
| octane |
114.2 |
216.22 |
209.11 |
3.287 |
324.16 |
359.41 |
10.87 |
| nonane |
128.2 |
219.71 |
229.08 |
4.263 |
411.95 |
419.16 |
1.750 |
| decane |
142.2 |
243.52 |
244.71 |
0.492 |
386.56 |
470.55 |
21.72 |
| undecane |
156.3 |
247.60 |
257.22 |
3.888 |
523.94 |
514.91 |
1.722 |
| dodecane |
170.3 |
263.62 |
267.40 |
1.434 |
525.72 |
553.45 |
5.266 |
| tridecane |
184.3 |
267.81 |
275.79 |
2.980 |
606.82 |
587.19 |
3.233 |
| tetradecane |
198.3 |
279.04 |
282.81 |
1.351 |
725.90 |
617.05 |
14.99 |
| pentadecane |
212.4 |
283.46 |
288.79 |
1.883 |
754.87 |
643.79 |
14.71 |
| heptadecane |
240.4 |
297.05 |
298.60 |
0.520 |
621.09 |
690.40 |
11.15 |
| eicosane |
282.5 |
310.09 |
310.35 |
0.083 |
805.40 |
749.70 |
6.916 |
| |
ΔT=100×|T(cal)-T|/T
|
Δε=100×|ε(cal)-ε|/ε
|
5 Conclusions
Parameters in the set S define the EoS for a substance and are functions of the molar weight M in the pseudo-alkane model. In this case, the functions b, c, and d are shown in Eq. (6), e and f are shown in Eq. (9), λ is shown in Eq. (10), and ε is shown in Eq. (11).
The last function, ε, was developed to minimize the mean square deviation of the melting temperature between the predicted and experimental values. In this case, the molar weight in the experimental data runs from 100 g/mol to 600 g/mol, the melting temperature results are in agreement with experimental data, and therefore, the model works at least in such a range.
Finally, the melting temperature deviation between both predictions, with the EoS in the Ref. [1] and the pseudo-alkane model, increases from pentane to butane, and in the worst cases, the model fails for methane, ethane, and propane. Furthermore, in the model, Eq. (11) is a smooth interpolation of the ε values until the eicosane and is an extrapolation for heavy n-alkanes.
Acknowledgments
The study was supported by CONACyT and Instituto Mexicano del Petróleo (Proyect number: Y.61005).
References
[1] J. M. Marín-García, A. Romero-Martínez, and F. J. Guevara-Rodríguez, Chem. Eng. Commun. 209 (2022) 171.
[ Links ]
[2] J. M. Marín-García, A. Romero-Martínez, and F. J. Guevara-Rodríguez, Rev. Mex. Fis. 66 (2020) 656.
[ Links ]
[3] F. J. Guevara-Rodríguez and A. Romero-Martínez, Fluid Phase Equilib. 247 (2013) 22.
[ Links ]
[4] Y. L. Guennec, S. Lasala, R. Privat, and J.-N. Jaubert, Fluid Phase Equilib. 427 (2016) 513.
[ Links ]
[5] F. J. Guevara-Rodríguez, Fluid Phase Equilib. 307 (2011) 190.
[ Links ]
[6] A. P. Kudchadker and B. J. Zwolinski, J. Chem. Eng. Data 11 (1966) 253.
[ Links ]
[7] A. Yokozeki, Int. J. Thermophysics 24 (2003) 589620.
[ Links ]
[8] A. Yokozeki, Fluid Phase Equilib. 222-223 (2004) 55.
[ Links ]
[9] A. Yokozeki, Int. J. Thermophysics 25 (2004) 643668.
[ Links ]
[10] A. Yokozeki, Appl. Energy 81 (2005) 322.
[ Links ]
[11] J. H. Lee, M. S. Shin, H. Kim, and K.-P. Yoo, J. Chem. Thermodynamics 42 (2010) 891.
[ Links ]
[12] J. H. Lee, M. S. Shin, and K.-P. Yoo, J. Chem. Thermodynamics 50 (2011) 41664176.
[ Links ]
[13] C. Mo, G. Zhang, Z. Zhang, D. Yan, and S. Yang, ACS Omega 7 (2022) 9322.
[ Links ]
[14] H. Wenzel and G. Schmidt, Fluid Phase Equilib. 5 (1980) 3.
[ Links ]
[15] D.-Y. Peng and D. B. Robinson, Ind. Eng. Chem. Fundam. 15 (1976) 59.
[ Links ]
[16] N. F. Carnahan and K. E. Starling, J. of Chem. Phys. 51 (1969) 635.
[ Links ]
[17] E. Lang and H. Wenzel, Fluid Phase Equilib. 51 (1989) 101.
[ Links ]
[18] G. Soave, Chem. Eng. Sci. 27 (1972) 1197.
[ Links ]
[19] Otto. Redlich and J. N. S. Kwong, Chem. Rev. 44 (1949) 233.
[ Links ]
[20] D. G. a and H. Wenzel, J. Supercrit. Fluids 15 (1999) 97108.
[ Links ]
[21] D.-Y. Peng and D. B. Robinson, Equations of State in Engineering and Research (American Chemical Society, Washington DC, 1979) Chap. 10, pp. 185-195.
[ Links ]
[22] D. V. Nichita, L. Goual, and A. Firoozabadi, SPE Production 16 (2001) 250.
[ Links ]
[23] C. Lira-Galeana, A. Firoozabadi, and J. M. Prausnitz, AIChE J. 42 (1996) 239.
[ Links ]
[24] K. W. Won, Fluid Phase Equilib. 30 (1986) 265.
[ Links ]











 nueva página del texto (beta)
nueva página del texto (beta)


