1. Introduction
Circadian cycles are physical, mental and behavioral variations that follow an approximately 24-hour rhythm. The field of chronobiology has been dominated by basic research questions such as what biological variables obey regular circadian cycles, what are the central and/or peripheral anatomical substrates that generate these rhythms [1, 2], and how one can distinguish between the rhythm of an internal circadian clock and the effects of masking or entraining because of external perturbations [3, 4]. It has become clear that most - if not all - variables of living systems obey circadian cycles, including bacteria [5], plants [6], insects [7], vertebrates in general [8] and humans in particular [9, 10, 11, 12] and cosinor analysis was established as the standard method to quantify these regularities in experimental data. Cosinor analysis uses a predetermined mathematical model of periodicity, in particular a cosine function, which is fitted to the data to describe the average cyclic behaviour over a given time period [13, 14].
Presently, since the universality of circadian cycles has been accepted, also more applied research questions are attracting attention, such as the analysis of irregularities in circadian rhythms as a proxy to assess pathological or sub-healthy conditions in the clinic, e.g., age-associated frailty [15], preclinical [16] or advanced dementia [17], hyperactivity and attention-deficit disorder [18], psychological vulnerability [19], insomnia [20], etc. Such irregularities are difficult to describe using cosinor analysis, but may be quantified using non-parametric approaches such as intradaily stability (IS) and intradaily variability (IV) [21, 22]. These non-parametric approaches make no attempt however to extract circadian (24h) or ultradian (<24h) cyclic components from the data. This may be unfortunate, because a common research method to explore an unknown system, in particular in electronic engineering or material science, is to stimulate that system using a calibrated test signal at a specific frequency and to investigate the amplitude and phase of the response signal, which in linear systems occurs at the same frequency [23, 24]. Similarly, circadian cycles can be interpreted as the reaction of the variables of a physiological system to the universal forcing of the alternation between day and night. The circadian parameters of mesor, amplitude, period and acrophase are of particular interest to evaluate this response, which may also depend on the specific role these variables play in homeostatic regulation [25, 26, 27, 28]. Additionally, not only the average values of the circadian parameters but also their day-to-day variability gives valuable information to distinguish between healthy and unhealthy populations [20].
Altough the extraction of circadian cycles from experimental data can be interpreted as a particular case of time-series analysis, it would appear that chronobiology and time-series analysis have developed according to different paths, and whereas various of the specialized time series techniques have occasionally been applied to rhythmobiology, no studies are available that compare the applicability between a variety of methods or for different variables. One of the objectives of time-series analysis is to decompose continuous data as the sum of more simple components such as a trend, (approximately) periodic components and fluctuations, and/or extract one or more specific components, with the presupposition that these individual time-series components may reflect specific physical or physiological phenomena or processes.
Different families of time-series methods exist, differing in the mathematical principles by which this decomposition or extraction is realized. The most common decomposition method is Fourier spectral analysis, where the time series is represented as the sum of sine and cosine periodic functions of different frequencies and amplitudes [29]. A drawback of Fourier spectral analysis is that strictly it may only be applied to stationary time series, i.e., where statistical measures such as average and variance do not change over time, which may be an issue in experimental time series that often have, e.g., dominant trends or irregular behaviour in time. More advanced time-series techniques decompose time series either into more general mathematical functions that do not need to be periodic, or generate the basis in a numerical and data-adaptive way from the data itself, and are intensively used to study nonstationary time series. Examples of the former strategy are wavelet-based methods [30, 31], such as the continuous wavelet transform (CWT) or the discrete wavelet transform (DWT), and derived methods such as nonlinear mode decomposition (NMD) [32, 33]. Examples of the latter strategy are subspace-based methods such as singular spectrum analysis (SSA) [34, 35, 36], and envelope-based methods such as the empirical mode decomposition (EMD) [37, 38] and derived methods such as the ensemble empiricial mode decomposition (EEMD) [39] and the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) [40].
The purpose of the present contribution is to explore the application of the before-mentioned traditional and more recent time-series techniques to study the circadian cycles of selected time series for a variety of physiological variables. The performance of these time-series techniques will be compared to standard cosinor analysis. The circadian parameters and their day-to-day variability will be discussed and will be interpreted within the context of homeostatic regulation
2. Materials and methods
2.1. Experimental time series
The present contribution is a secondary analysis of simultaneous time series of 5 different variables showing the effect of the alternation of day and night on the physiology of a healthy male young adult during 1 week of continuous monitoring. Whereas in previous publications the high-frequency spontaneous fluctuations of these time series were studied from the perspective of homeostatic regulation [25, 27], the objective here is to analyze the circadian cycles. Figure 1 shows actigraphy (act), which measures the number of movements per sample time interval or ‘epoch’, in the present case arbitrarily chosen as 1min, using the Actigraph wGT3X-BT device, the cardiovascular variables of heart rate (HR) measured in beats per minute (bpm) and systolic blood pressure (BP) measured in millimeters of mercury (mmHg), both registered using the CONTEC ABPM50 device, and thermoregulatory variables of skin temperature (Tskin) and core temperature (Tcore), measured in degrees Celsius (°C) using Maxim Thermochron DS1922L iButtons (“thermochron8k”). All time series have been resampled at the same rate of 1/(15 min) and all start at midnight. Unless otherwise stated, all time-series analyses have been carried out with Wolfram Mathematica, version 12.0.0.0.
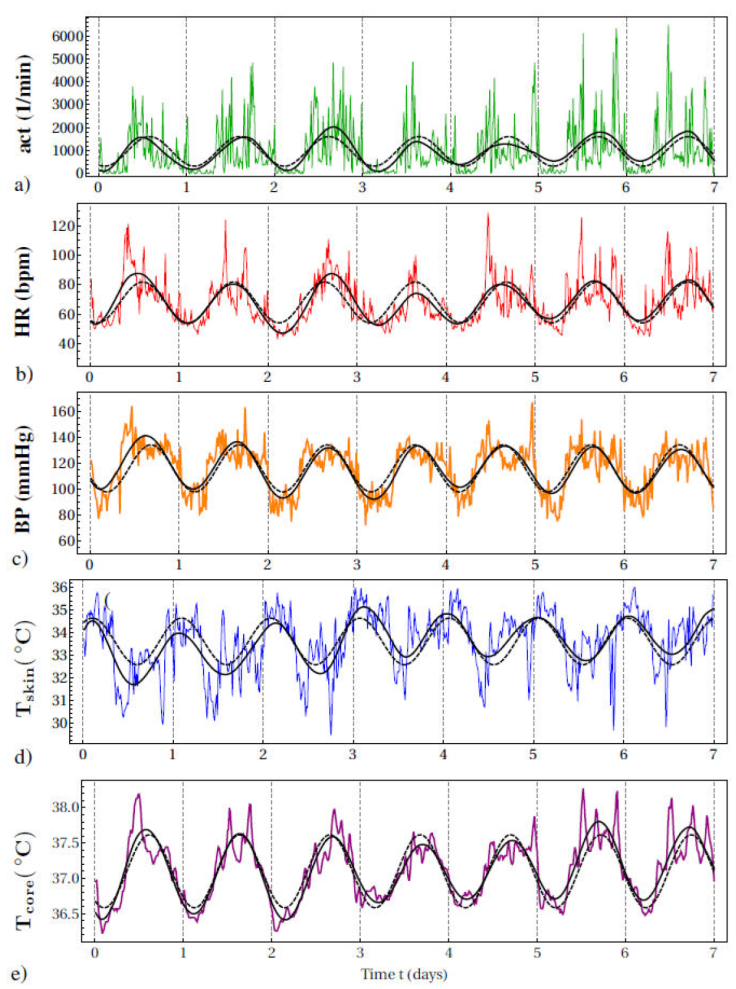
Figure 1 7-day continuous monitoring of a healthy male young adult showing (a) actigraphy (act) expressed as number of movements per minute (1/min), cardiovascular variables of (b) heart rate (HR) as beats per minute (bpm) and (c) systolic blood pressure (BP) as millimeters of mercury (mmHg), and thermoregulatory variables of (d) skin temperature (Tskin) and (e) core temperature (Tcore) as degrees Celsius (°C). Sample frequency is 1/(15 min) for all variables. Vertical gridlines indicate midnight. Also shown are the approx. 24h circadian cycle, estimated by cosinor analysis which shows the 7-day average properties (dashed curve) and SSA which also reflects the day-to-day variability (continuous curve).
2.2. Time-series techniques
2.2.1. Cosinor
The traditional method to study the periodic aspects of circadian rhythms is cosinor analysis, see [13, 14]. The cosinor approach is based on regression techniques and is applicable to equidistant or non-equidistant time series x(n) of N discrete data points,
The procedure consists of fitting a periodic function y(t) to time series x(n),
where the angular frequency
2.2.2. Frequency domain filter (FDF)
Also called spectral domain filter, Fourier domain filter or FFT domain filter, or - more informally - Fourier filter, Fourier transform filter or FFT filter. Filtering is one of the most common forms of signal processing which has as a goal to remove specific frequencies or frequency bands, and/or improve the magnitude, phase or group delay in some part (s) of the spectrum of a signal [43]. Mathematically, a filter corresponds to the convolution of signal x(t) with the impulse response g(t) of the filter to obtain a filtered signal c(t),
but this shift-and-multiply procedure may be very time-consuming for longer signals. In the Fourier domain, or frequency domain, the convolution reduces to a much simpler and efficient point-to-point multiplication [44],
over a certain angular frequency range
and similarly
FDF appears to have been applied to extract circadian cycles from experimental data only once [46]. Other types of digital filter have occasionally been applied, such as Butterworth filters [47], finite impulse response filters (FIR) [48], Kalman filters [49, 50], adaptive notch filters [51], particle filters [52, 53], Bayesian filters [54] and waveform filters [55]. Here, an FDF bandpass filter is used. In order to capture the circadian cycle at ω ≈ 7 (in units of number of oscillations during 7 successive days) and the day-to-day variability, a simple rectangular filter window is applied in the arbitrary range 0 ≤ ω ≤ 12, excluding the ultradian oscillations which may be expected to start to appear near ω ≈ 14 and where ω = 0 corresponds to the constant DC or mesor term.
2.2.3. Wavelet transforms (WT)
Wavelet analysis is an example of time-frequency analysis, i.e., the time and frequency domains are studied simultaneously, such that this approach is particularly well suited for the study of non-stationary processes [30, 31]. Two versions of wavelet analysis exist: (i) the continuous wavelet transform (CWT), which tends to be used more in scientific research to analyze complex signals and is superior from the viewpoint of visualizing results for individual signals, but has the drawback of using a non-orthonormal basis such that the CWT expresses excessive information and the values of the wavelet coefficients are correlated; (ii) the discrete wavelet transform (DWT) which is preferred in order to solve technical real-life problems and where orthonormal bases are available that allow a signal decomposition in an efficient and exact way, with considerable advantages such as computational speed, simpler procedure for the inverse transform and application to multiple signals [30, 31]. One important problem when using CWT or DWT is the choice of an appropriate mother wavelet or analizing wavelet, which will depend on the type of signal studied and/or the study objective, and where an inadequate choice may compromise the results.
The Continuous Wavelet Transform (CWT) [30, 31] is performed by convolution of the signal x(t) with the two parameter wavelet function ψ s,τ (t),
where the asterisk denotes the complex conjugate and the wavelet function is obtained from the mother wavelet or analyzing wavelet,
where the parameter t specifies the wavelet location on the time axis, τ expresses a shift or translation and s corresponds to an expansion (dilation) of the width of the wavelet in the time domain and represents the time scale of the wavelet transform. Often, the notion of “period” T is considered instead of the “time scale” s since it is more suitable in many studies, but one has to be very careful because the identity T = s is correct only for special choices of the mother wavelet and its parameters. The main difference between Eqs. (5) and (6) is that the Fourier transform
Discrete Wavelet Transform (DWT) [30, 31] DWT uses a logarithmic discretization of the mother wavelet function of Eq. (7),
which may constitute an orthonormal basis and where commonly the discrete wavelet parameters are chosen as
are called detail coefficients or wavelet coefficients, and
are approximation coefficients. The inverse transformations,
are called the signal details and the smooth or continuous approximation of the signal at scale m. DWT works in a recursive way, decomposing the signal
allowing to reconstruct the original signal as a multiresolution series expansion,
which is the sum of all the signal details and a single residual continuous approximation. In the case of a power-of-two logarithmic scaling as presented here, the maximum number of signal details in which the signal is decomposed is
2.2.4. Singular Spectrum Analysis (SSA)
SSA is an example of a subspace or phase-space method and is closely related to embedding and attractor reconstruction of dynamical systems [34]. SSA has been discussed in detail in a number of textbooks [34, 35, 36, 62]. A standard and very extensive reference is [63], whereas a short and very accessible introduction can be found in [64]. Unlike Fourier or wavelet analysis, which express a signal as a superposition of predefined functions, SSA is considered to be data adaptative or model and user independent, because the basis functions are generated from the data itself. SSA can be explained as a 3-step process. First, the univariate signal x(n) with length N is embedded into a so-called trajectory matrix
X, by sliding a window with length L over the data using unitary steps, such that the dimension of the matrix is K × L where
Here,
where
2.2.5. Empirical Mode Decomposition (EMD) and related methods
Similar to SSA, EMD is a data-adaptive method, but its approach is empirical instead of analytical and focused on the upper and lower envelopes of the time series [37, 38]. The goal of this method is to decompose the original signal into a collection of intrinsic mode functions (IMFs), which are simple oscillatory modes with meaningful instantaneous frequencies, and a residual trend. This requirement is enforced by the following conditions: (1) the number of zero crossings and the number of local extrema of the function must differ by at most one and (2) the “the local mean” of the function is zero. The sifting process by which the signal is decomposed is the following: First, the local maxima are identified and connected by a cubic spline line, constructing the upper envelope. This procedure is repeated with the local minima to construct the lower envelope. Then, the average of these envelopes is designated as a local mean of the signal, designated as
which can be repeated k times until
EMD separates different frequency scales of the signal into separate IMFs, but it is not guaranteed that (when analyzing data from some natural process) each IMF represents a physical time scale of the process. Often ranges of IMFs need to be added together to reconstruct information pertaining to a single natural time scale [39], constituting a problem with the so-called mode mixing, and some IMF components may represent the properties of measurement noise instead of the underlying physical process. To assist in selecting the IMFs with a physical meaning [70] a statistical significance test has been proposed which compares the IMFs against a null hypothesis of white noise. The EMD has only rarely been applied before to analyze circadian, ultradian and infradian rhytyms [16,71].
In order to solve in great part the mode-mixing problem and extract more robust and physically meaningful IMFs, a variant of EMD is used, called Ensemble Empirical Mode Decomposition (EEMD) [39], which performs EMD over an ensemble of the signal plus Gaussian white noise. The EEMD has been applied before to analyze circadian and infradian rhythms [72, 73]. However, the EEMD does not allow a complete reconstruction as in Eq. (16), since the original signal cannot be exactly recovered by adding together its EEMD components. In order to overcome this situation, a second variant called the Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) is used [40, 74], this procedure adds a particular noise at each stage, and achieves a complete decomposition with no reconstruction error. Apparently, CEEMDAN has never been applied to analyze circadian rhythms.
All calculations for EMD, EEMD and CEEMDAN in this contribution were carried out with the free Python package libeemd [75].
2.2.6. Nonlinear mode decomposition
NMD is another data-adaptive method, but in contrast to SSA and EMD it focuses on obtaining time-series components that have a more obvious physical meaning [32, 33]. It is based on the combination of time-frequency analysis [32, 76], surrogate data tests [77] and the idea of harmonic identification [78]. Given that experimental signals are rarely pure sinusoidal, the NMD considers the full nonlinear modes (NM) in the signal, which are defined as the sum of all components that correspond to the same activity,
where A(t) and ϕ(t) are the instantaneous amplitude and phase, respectively, and
To do this, four steps are necessary:
Extract the fundamental harmonic of a nonlinear mode (NM) accurately from the signal’s time-frequency representation (TFR), in this case, using the same Lognormal wavelet as in CWT.
Find candidates for all its possible harmonics, based on its properties.
Identify the true harmonics (i.e., corresponding to the same mode), and confirm by surrogate testing.
Reconstruct the full NM by summing together all the true harmonics; subtract it from the signal, and iterate the procedure on the residual until a preset stopping criterion is met.
NMD has been applied only in a few occasions to analyze circadian cycles [68, 79].
2.3. Goodness of fit
The coefficient of determination or goodness of fit R
2 is an important parameter to evaluate the quality of the extracted circadian rhythms. R
2 compares the variance of the residual errors
2.4. Correlation coefficients
In the following, correlation coefficients are used to compare the circadian cycles extracted by different methods. The Pearson correlation coefficient is a measure of the linear correlation between two variables. It has a value between +1 and -1, where 1 is total positive linear correlation, 0 is no linear correlation, and -1 is total negative linear correlation. The Pearson correlation coefficient
where cov(x, y) is the covariance between time series x and y, and
If there are no repeated data values, a perfect Spearman correlation of +1 or -1 occurs when each of the variables is a perfect monotone function of the other.
3. Results
3.1. Circadian parameters
Approx. 24 h circadian cycles were extracted for the continuous data of all variables considered: actigraphy (act), heart rate (HR), blood pressure (BP), skin temperature (Tskin) and core temperature (Tcore), see Fig. 1 for a plot of these cycles as extracted by cosinor analysis and SSA. Whereas by construction cosinor analysis represents the circadian cycle as a periodic function with constant circadian parameters that reflect the average behaviour over the whole period considered, 7 successive days in the present case, the other methods show a circadian cycle that varies over time and allow to extract daily estimates of the circadian parameters, e.g.,
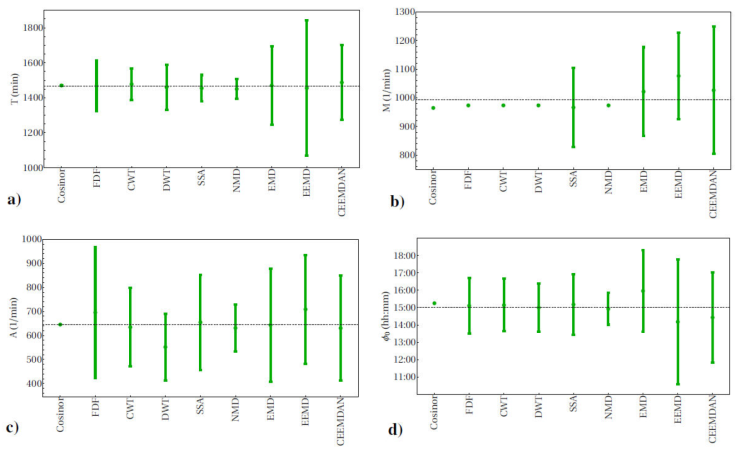
Figure 2 Circadian parameters for actigraphy. a) period T, b) mesor M, c) amplitude A and d) acrophase ϕ 0. Week-average values are shown and, where possible, also error bars with the standard deviation of the day-to-day variability. Also the mean value for each parameter over all methods is indicated (horizontal lines).
3.2. Goodness-of-fit of circadian cycles
Table I shows the estimations of the coefficient of determination R
2 by the different methods considered for the circadian cycles for all variables. An ANOVA test indicates that the between-group variance for R
2, i.e., variance between different variables, is larger than the within-group variance, i.e., the variance of R
2 values between different methods for the same variable (Fratio=1255 with
Table I Coefficient of determination or goodness-of-fit parameter R 2 of Eq. (19) shown in percentage, for the circadian cycle estimated by different methods for all variables.
| R 2 (%) | |||||
|---|---|---|---|---|---|
| act (1/min) | HR (bmp) | BP (mmHg) | Tskin (°C) | Tcore (°C) | |
| Cosinor | 16.0 | 38.7 | 50.2 | 29.5 | 69.3 |
| FDF | 20.5 | 48.6 | 57.4 | 41.9 | 75.2 |
| CWT | 17.8 | 39.3 | 51.9 | 31.4 | 68.4 |
| DWT | 19.9 | 44.3 | 56.4 | 35.1 | 74.9 |
| SSA | 21.3 | 49.4 | 57.4 | 42.7 | 76.7 |
| NMD | 16.7 | 43.3 | 53.3 | 28.9 | 74.9 |
| EMD | 14.6 | 42.5 | 52.7 | 24.0 | 76.0 |
| EEMD | 27.2 | 51.7 | 66.3 | 49.9 | 72.0 |
| CEEMDAN | 20.5 | 53.1 | 45.1 | 33.8 | 80.1 |
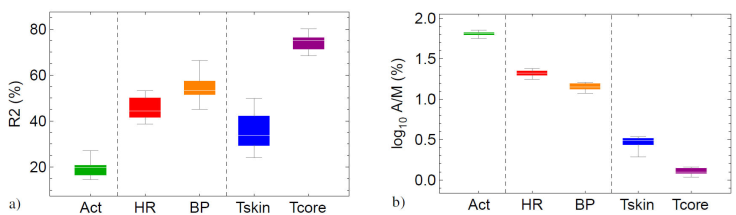
Figure 3 Selected parameters to characterize circadian cycles of actigraphy (act), heart rate (HR), blood pressure (BP), skin temperature (Tskin) and core temperature (Tcore): a) coefficient of determination R 2 and b) modulability A/M. The graphs illustrate that the parameter values depend primarily on the variable and much less on the specific method used to calculate the circadian parameters. A/M is shown in logarithmic scale to more clearly show differences in the rather small values for core and skin temperature. Variables are separated according behavioural, cardiovascular and thermoregulatory mechanisms (vertical gridlines).
For specific variables, compared to cosinor analysis, the other methods tend to improve the description of the circadian cycle with up to 10 - 20 %. Exceptions are the EMD analysis of actigraphy and skin temperature, and CEEMDAN for blood pressure, where the description is worse down to -5% than for cosinor analysis, possibly due to the mode-mixing problem typical for these methods. Results for CWT and NMD only slightly improve the cosinor description, whereas DWT only gives an average performance when compared to the other methods. Maximal R 2 values are obtained with EEMD for the particular variables of actigraphy, blood pressure and skin temperature, and with CEEMDAN for heart rate and core temperature. On the other hand, only SSA and FDF give a consistent above-average description in general for all variables.
3.3. Spectral content of circadian cycles
Figure 4 shows the spectral content, i.e., the Fourier power spectra, of the circadian cycles as found by the different methods for actigraphy. Similar results are obtained for the other variables of heart rate, blood pressure and core and skin temperature. By construction, circadian cycles described by the cosinor analysis of Eq. (2) should correspond to a spectrum with a single peak at the circadian frequency of f ≈ 7 (cyles/7 days), but because of the phenomenon of spectral leakage small power contributions are also present at neighbouring frequencies [80]. Comparing the spectra of other methods to the spectrum of cosinor analysis gives a measure of how different estimates of the circadian cycle are constituted of different combinations of lower and higher frequencies. Frequencies of spectra of filter-based methods such as FDF and DWT cut off abruptly and are exactly 0 outside of a specific bandpass range. Spectra are rather narrow for DWT, NMD and CWT, reflecting more regular circadian cycles. The spectrum for EMD, on the other hand, is very wide, corresponding to a more irregular estimate of the circadian cycle. Spectra for SSA, EEMD and CEEMDAN have in-termediate widths, indicating a description of the circadian cycles that may be moderately irregular. EMD, EEMD and CEEMDAN also tend to have frequency contributions that are not contained within the original signal.
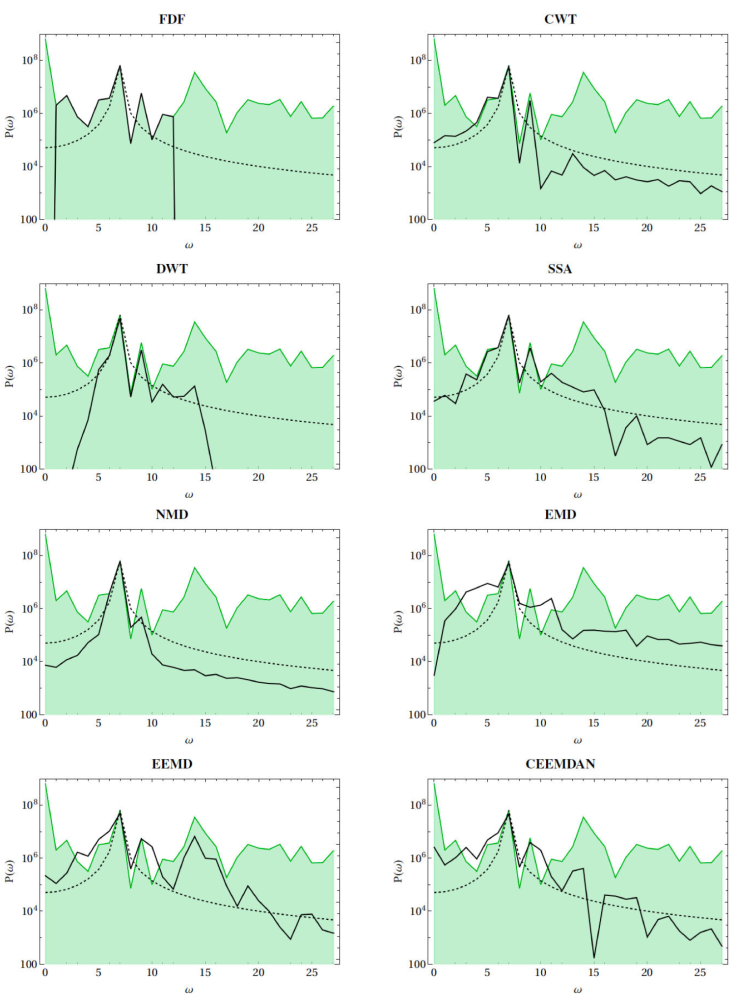
Figure 4 Fourier power spectra of time series of actigraphy (green shaded curves), circadian cycles as extracted by different methods (black continuous curves), and compared to standard cosinor analysis (black dashed curve). All spectra are presented in semilogarithmic scale. Angular frequencies ω are shown in units of number of cycles for 7 consecutive days.
3.4. Correlation between circadian cycles extracted by different methods
Table II shows the Spearman correlation coefficients between circadian cycles as estimated by the different methods applied to actigraphy data. Similar results are obtained for the other variables of heart rate, blood pressure and core and skin temperature. The correlation coefficients are rather large and mostly in the range 0.75-0.95, which is unsurprising because it is always the same process of the circadian cycle that is described and which is only observed from the perspectives of different methods. For all variables, DWT and SSA are the methods for which the circadian cycles correlate always above average with the other methods. Another method for which the circadian cycles tend to correlate above average with those of other methods are CWT and NMD. Methods for which extracted cycles tend to correlate less than average with those of other methods are EMD, EEMD and CEEMDAN.
Table II Spearman’s rank correlation coefficient ρ of Eq. (21) for circadian cycles estimated by different methods for actigraphy.
| ρ | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Cosinor | FDF | CWT | DWT | SSA | NMD | EMD | EEMD | CEEM-DAN | |
| Cosinor | 1 | 0.876 | 0.936 | 0.936 | 0.938 | 0.950 | 0.814 | 0.767 | 0.822 |
| FDF | 0.876 | 1 | 0.930 | 0.945 | 0.950 | 0.908 | 0.745 | 0.852 | 0.893 |
| CWT | 0.936 | 0.930 | 1 | 0.971 | 0.979 | 0.949 | 0.865 | 0.867 | 0.938 |
| DWT | 0.936 | 0.945 | 0.971 | 1 | 0.982 | 0.971 | 0.789 | 0.868 | 0.895 |
| SSA | 0.938 | 0.950 | 0.979 | 0.982 | 1 | 0.960 | 0.813 | 0.874 | 0.911 |
| NMD | 0.950 | 0.908 | 0.949 | 0.971 | 0.960 | 1 | 0.753 | 0.837 | 0.877 |
| EMD | 0.814 | 0.745 | 0.865 | 0.789 | 0.813 | 0.753 | 1 | 0.729 | 0.812 |
| EEMD | 0.767 | 0.852 | 0.867 | 0.868 | 0.874 | 0.837 | 0.729 | 1 | 0.895 |
| CEEM-DAN | 0.822 | 0.893 | 0.938 | 0.895 | 0.911 | 0.877 | 0.812 | 0.895 | 1 |
4. Discussion
4.1. Time-series description of circadian cycles
Compared to standard cosinor analysis, the other methods in general improve the goodness-of-fit R 2 of the circadian cycle. Comparing between all methods, SSA, EEMD, FDF and CEEMDAN perform above average, DWT on average, and NMD, EMD and CWT below average. In particular, the good performance of FDF is surprising given that it is one of the simplest filter techniques available and that here a crude rectangular filter window was applied. This good performance may be explained by the broad bandpass frequency range that was chosen. An alternative approach in the literature is to describe the circadian cycle by the fundamental frequency of ≈ 1/24h together with its higher harmonics [17]. Also the NMD description is based on harmonics, but appears to underperform in comparison with other methods. A possible reason is that all frequency-based methods utilized for rhythm detection suffer from the lack of specification [71, 81], such that harmonics may be due to ultradian rhythms or non-stationarities and may not be appropriate to describe the circadian cycle. Whereas in the case of FDF and other digital filters the frequency range needs to be defined by the user and may be arbitrary, methods such as SSA, EEMD and CEEMDAN generate their time-series components and the corresponding frequency ranges in a data-adaptive way. These frequency ranges are moderately wide, and appear to maximize R 2 in comparison with either narrower (cosinor, CWT, DWT and NMD) or wider frequency ranges (EMD), see Fig. 4. The circadian cycles derived by EEMD and CEEMDAN correlate less well with the cycles extracted by other methods, it is is therefore possible that these EMD-based techniques capture more specific features of experimental data which are not accessible to other methods, and it seems that EEMD and CEEMDAN are more applicable to some variables than to others. In contrast, circadian cycles described by SSA correlate above average with results from other methods and therefore appear to capture general properties of experimental data. Also, SSA appears to give a good description of circadian cycles independently from the specific variable that is studied, perhaps because the circadian cycle may be a limit circle [82] or a chaotic attractor [83] which subspace or phase-space methods such as SSA may detect very well. Overall, it appears that data-adaptive methods are particularly suited to extract the circadian cycle from experimental data. In this section, the goodness-of-fit obtained by specific methods was emphasized because it is hypothesized that larger R 2 values will allow to statistically distinguish more easily between healthy and unhealthy populations in clinical applications of circadian cycles.
4.2. Circadian parameters and day-to-day variability
All methods considered agree rather well on the average values of the circadian parameters for all methods. These average values are mostly within the error bars representing the day-to-day variability according to each method. Ref. [20] presented evidence that not only the average values of the circadian parameters but also the day-to-day variability contribute to distinguish between healthy and unhealthy populations. The present contribution demonstrates that one of the main differences between various methods is their quantification of the day-to-day variability. It is not clear what part of this variability is due to the data itself (intrinsic) and what part may be artificially produced by the specific method applied (extrinsic). Here, it is hypothesized that if a method is consistent in the quantification of day-to-day variability, and the extrinsic part of the variability is similar for different populations, then differences in this variability between the populations must be due to physiological effects. If this condition is fulfilled, then day-to-day variability may indeed be applied for diagnostic purposes as proposed before [20].
4.3. Homeostatic interpretation of circadian parameters
The range of R 2 for the circadian cycles for all variables considered here is very wide, 15 - 80%, see Table I, and in the following this wide range will be interpreted. Refs. [25, 26, 27, 28, 84, 85, 86] proposed that physiological variables that play different roles in homeostatic regulation exhibit different time-series behavior with distinct statistical properties. In particular, it was suggested that regulated variables such as blood pressure and core temperature fluctuate within a narrow range around a specific setpoint representing Claude Bernard’s constant internal environment; on the other hand, effector variables such as heart rate and skin temperature are responsible for Walter Cannon’s adaptive responses to internal and external perturbances and are much less restricted in space and time. Therefore, it was proposed that in optimal conditions of youth and health effector variables are more variable and less regular than regulated variables. This paradigm was investigated for the spontaneous fluctuations of physiological variables in rest and in absence of dominant stimuli. It is unclear whether a similar phenomenology can be expected in the presence of an external forcing such as the alternation of day and night. The coefficient of determination R 2 as determined by the different methods appears to respond affirmatively to this question, see Table I and Fig. 3a), the regulated variables considered in this contribution (blood pressure and core temperature) indeed appear to be associated to more regular time series (higher R 2 values), and effector variables (heart rate and skin temperature) to more irregular or variable time series (lower R 2 values). Actigraphy could be an example of a third category of variable related to behavior or conductome, see [87], corresponding to very irregular time series (minimal R 2 values). To investigate this paradigm further, a derived measure A/M is proposed, called modulability for the purpose of this contribution, which expresses amplitude A as a percentage of mesor M, and therefore is dimensionless allowing comparisons between different variables. Table III and Fig. 3b) show that for a specific homeostatic mechanism, modulability appears to be larger for the effector variable than for the corresponding regulated variable. For the thermoregulatory mechanism A/M ≈ 3 for skin temperature vs. ≈ 1.3 for core temperature. For the cardiovascular mechanism A/M ≈ 21 for heart rate vs. ≈ 15 for blood pressure. This sounds very reasonable because regulation tries to maintain regulated variables within a very narrow homeostatic range, whereas the range of regulating variables is contained only by what is physiologically possible and what not. Modulability for behavioural variables such as actigraphy is even larger, A/M ≈ 65, because here there are no physiological limitations that must be respected. It is hypothesized that there may be a relation between this homeostatic time-series paradigm and the phenomena of masking and entrainment in rhythmobiology. In particular, it is suggested that effector variables are more prone to the effects of masking and entrainment than regulated variables, such that the latter may be expected to reflect more easily the “true” cycles of the internal circadian clocks.
Table III Modulability A/M shown in percentage, for the circadian cycles estimated by different time-series techniques for all variables.
| A/M (%) | |||||
|---|---|---|---|---|---|
| act (1/min) | HR (bmp) | BP (mmHg) | Tskin (°C) | Tcore (°C) | |
| Cosinor | 66.9 | 20.4 | 15.6 | 3.07 | 1.39 |
| FDF | 71.4 | 22.2 | 16.1 | 3.21 | 1.44 |
| CWT | 65.2 | 18.0 | 13.2 | 2.64 | 1.09 |
| DWT | 56.7 | 17.7 | 13.3 | 2.76 | 1.25 |
| SSA | 67.8 | 20.6 | 15.8 | 3.07 | 1.35 |
| NMD | 64.8 | 21.6 | 14.1 | 3.41 | 1.25 |
| EMD | 63.0 | 24.1 | 15.4 | 2.75 | 1.40 |
| EEMD | 65.9 | 21.1 | 13.7 | 3.44 | 1.15 |
| CEEMDAN | 61.4 | 22.5 | 11.8 | 1.92 | 1.23 |
4.4. Strengths and limitations
The strengths of the present contribution are the inclusion of 5 different variables (actigraphy, heart rate, blood pressure, skin temperature and core temperature) from 3 different mechanisms (behavior, cardiovascular and thermoregulatory) and 9 different methods (cosinor, FDF, CWT, DWT, SSA, EMD, EEMD, CEEMDAN, NMD) from at least 4 different domains (mathematical model, time-frequency, analytical data-adaptive and empirical data-adaptive). The limitation is obviously that only data of a single subject was included. Therefore, the results of the present contribution are presented as hypotheses which should be rather straightforward to verify and which may inspire further investigations.
5. Conclusion
A good description of circadian cycles appears to depend on including an adequate broad frequency range around the central frequency of 1/24h, rather than including harmonics of this fundamental frequency. Recent time-series techniques such as SSA, EEMD and CEEMDAN generate their components and the corresponding frequency content in a data-adaptive way, maximize goodness-of-fit R 2 values and appear to be particularly suited to extract circadian cycles from experimental data. Whereas EEMD and CEEMDAN may be more applicable to some variables than to others, the applicability of SSA appears to be more independent of the specific variable under study. Another advantage with respect to the traditional cosinor approach is that these time-series techniques allow to describe the day-do-day variability of the circadian parameters apart from their average values. Finally, several of the circadian parameters were interpreted within the context of homeostatic regulation and a possible link was proposed with the phenomena of masking and entrainment in rhythmobiology.











 nueva página del texto (beta)
nueva página del texto (beta)


